分段线性连续函数的下方图形拓扑结构

陈满春，黄若婷，庄方敏，李婷爽

（韩山师范学院 数学与统计学院，广东 潮州 521041）

1 引言

设(X，d)是一个度量空间，cld(X)是由X 所有非空子集构成的集族．

对任意A,B ∈cld(X)．

其中Bd(A,t)={x ∈X|d(x,A)＜t}．

当X是紧，dH是cld(X)上的一个度量，称为Hausdorff度量，其诱导出的拓扑称为Hausdorff度量拓扑．用USC(X)表示X 到单位区间I 上的所有上半连续函数之集，用C(X)表示X 到I 的所有连续函数之集．对任意f ∈USC(X) ，令↓f={(x,t)| 0 ≤t ≤f(x), x ∈I}．即↓f 为f 的下方图形．对任意A ∈USC(X),↓A={↓f|f ∈A}，显然↓f ∈cld(X)．因此，↓USC(X)和↓C(X)是cld(X)的子集，可对它们赋予Hausdorff度量拓扑．

文献[1]-[7]研究了↓USC(X)和↓C(X)的拓扑结构，得到了不少研究成果．其中包括下面一个重要的结论：

定理A 设X 为一个可分紧度量空间，则↓USC(X)≈（同胚于） Q，其中Q=[-1,1]∞为希尔伯特方体．

设s=[-1,1]∞，它是Q 的重要子空间．设S*={1/n:n ∈N+}为一收敛数列．用K 表示从区间(0,1]到[0,1]且分段点之集为S*的分段线性连续函数全体（如图1）．

对K 中的每个函数补充其在0 点的函数值为其上极限，得到一个新的集合L ，它是USCL={f ∈USC(I)f|(0,1]∈K}的子集．

图1 K 中的一个元素

令G={f ∈USCL|f(0)=O}．对↓USCL,↓G,↓L 赋予Hausdorff度量拓扑，即看为↓USC(I)的子空间．本文将证明如下结论（“≈”表示“对同胚于”）：

定理1.1 (↓USCL,↓G)≈(Q，s)．

定理1.2 (↓USCL,↓L)≈(Q，s)．

2 定理证明

设S=S*⋃{0},CO(S)={f ∈USC(S)|f(0)=0}，在文献[7]中证明了：

引理2.1 (↓USC(S),↓CO(S))≈(Q,s))．

应用上面的引理可以证明定理1.1．

定理1.1证明 构造函数

h: USC(S)→USCL 如下：

当x ∈S,h(f)(x)=f(x);

当x ∈[1/(n+1),1/n]时，h(f)(x)定义为f(1/n)和f(1/(n+1))的加权平均值．

定义 ↓h: ↓USC(S)→↓USCL 为↓h(f)=↓h((↓f))．

由引理2.1 ↓USC(S)≈Q 故↓USC(S)为紧集，容易验证h 是双射，从而↓h 是双射，故要原命题得证只需证明↓h 连续．

下证↓h 是连续的，其等价命题是：

（2.1）对任意ε ＞0，存在δ ＞0，若dH(↓f,↓g)＜δ，则dH(↓h(f),↓h(g))＜ε．

而dH(↓h(f),↓h(g))＜ε 又等价于下面（2.2），（2.3）同时成立：

（2.2）对任意(x,t)∈↓h(f)，存在(x1,t1)∈↓h(g)，使得d((x,t), (x1,t1))＜ε．

（2.3）对任意(x,t)∈↓h(g)，存在(x1,t1)∈↓h(f)使得d((x,t), (x1,t1))＜ε．

下证（2.2）成立．对任意ε ＞0，取δ=ε/4，对任意(x,t)∈↓h(f)．

当x=0 时，由h 的定义及dH(↓f,↓g)＜ε 知（1）式成立．

当x=I{0}时，因I{0}= ⋃∞

n=1[1/(n+1),1/n]，故存在m ∈N，使得x ∈[1/(m+1),1/m]，

下面在某个区间[1/(m+1),1/m]讨论：因为dH(↓f,↓g)＜δ，故对(1/(m+1), f(1/(m+1)))∈↓f ，存在 (1/NO,tO)∈↓g ， 使 得 d((1/(m+1), f(1/(m+1)), (1/NO,tO))＜δ ． 对 (1/m,f(1/m))∈↓f ， 存 在(1/N1,t1)∈↓g，使得

d((1/m,f(1/m)),(1/N1,t1))＜δ．其中N0,N1∈N．

（1）当m+1=N0,m=N1时， f(1/(m+1)-g(1/(m+1))＜δ， f(1/m)-g(1/m)＜δ，

因h(f)∈USCL，所以|h(f)(x)-h(G)(x)|≤max{|f(1/(m+1)-g(1/(m+1)|,|f(1/m)-g(1/m)|}＜δ．

对于任意(x,f(x))∈↓h(f)，存在(x,g(x))∈↓h(g)，使得d((x,f(x)),(x,g(x)))＜δ ＜ε．

由t ≤f(x)，存在x,t'∈↓h(g)，使得d((x,t),(x,t'))＜ε，故（2.2）式成立．

（2）当m+1 ≠N0或m ≠N1时，

注意到[|(1/n)-(1/(n+1))|:|(1/(n+1))-(1/(n+2))]≤3 恒成立，故有

因h(f)∈USCL，故min{f(1/(m+1)),f(1/m)}≤t ≤max{f(1/(m+1)),f(1/m)}．

当t1≥t0时，注意到|t-t1|＜δ．如果t ≤t1，存在((1/m),t)∈↓g，使得

如 果 t ＞t1， 存 在 ((1/N1),t1)∈↓g ， 使 得 d((x,t),((1/N1),t1))＜4δ=ε ． 注 意 到((1/N1),t1)),((1/N1),t))∈↓h(g)，当t1＜t 时也成立，故（2.2）式得证．同理可证（2.3）式成立．故↓h是一个同胚映射．又显然有h(G)=C0(S)，故(↓USCL,↓G)对同胚于(↓USC(S),↓C0(S))，由引理2.1，证毕．

在证明定理1.2之前先给出同伦稠的定义及相关结论．

定义2.1[8]空间X 的子集Y 在X 中同伦稠，指的是存在一个同伦h:X×I →X 使得h0=id(X)且ht(X)⊂Y 对任意t ＞0 都成立．容易验证s 在Q 中同伦稠．

引理2.2[8](Q,X)≈(Q,s)当且仅当X 是Q 的Gδ-集且X 和QX 都在Q 中同伦稠．

定理1.2证明 由引理2.2知，要证

(↓USCL,↓L)≈(Q,s) 的充分必要条件是：↓L 是↓USCL 的Gδ集，且↓L 及↓USCL↓L 在↓USCL 中同伦稠．

首先证↓L 是↓USCL 的Gδ集．令

再证↓L 及↓USCL↓L 在↓USCL 中同伦稠．由定理1.1 知↓G ≈s，故↓G 在↓USCL 中同伦稠，又因↓G ⊂↓L ⊂↓USCL，故↓L 在↓USCL 中同伦稠．令D=USCLL，下证↓D 在↓USCL 中同伦稠．构造映射

H:USCL×I →USCL 如下：

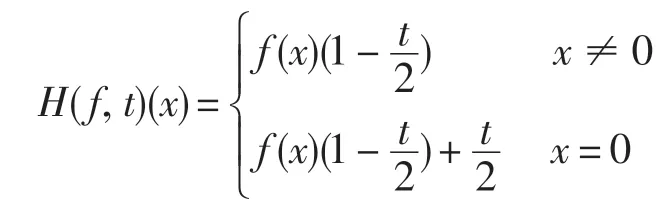
显然H(f,0)(x)=f(x)，且对任意t ∈(0,1]，有Ht(USCL)⊂D．定义↓H:↓USCL×I →↓USCL 为↓H(↓f,t)=↓[H(f,t)]．因此下面只需证↓H 连续．对任意ε ＞0，取δ=ε/2，当

d'((↓f1,t1),(↓f2,t2))＜δ 时（这里d'((↓f1,t1),(↓f2,t2))＜δ=max{dH(↓f1,f2),|t1-t2|}，易验证d'是度量．） dH(H(↓f1,↓t1),H(↓f2,t2))≤dH(H(↓f1,t1),H(↓f2,t2))+dH(H(↓f1,t2),H(↓f2,t2))≤(|t1-t2|/2)+dH(H(↓f1,↓f2)＜ε．

故↓H 是连续的．证毕．

致谢：感谢吴拿达老师对本文的建议和指导！

[1]YANG Z．WU N．A topological position of the set of continuous maps in the set of upper semicontinuous maps[J]．Science in China，Ser．A：Mathematics，2009，52（8）：1815-1828．

[2]YANG Z．ZHOU X．A pair of spaces of upper semi-continuous maps and continuous maps[J]．Topology Appl．，2007，154：1737-1747．

[3]YANG Z．WU N．The hyperspace of the regions below of continuous maps from S×S to I[J]．Questions and Answers in General Topology，2008，26：29-39．

[4]ZHANG L．YANG Z．The regions below compact-supported upper semicontinuous maps[J]．Houston J．Math．，2008，34（3）：781-792．

[5]YANG Z．The hyperspace of the regions below of all lattice-value continuous maps and its Hilbert cube compactification [J]．Science in China，Ser．A：Mathematics，2005，48：469-484．

[6]吴拿达，杨忠强．一类非紧度量空间上的连续函数空间[J]．数学进展，2013，42（4）：535-541．

[7]YANG Z．FAN L．The hyperspace of the regions below of continuous maps from the converging sequence[J]．Northeast Math，J．2006，22（1）：45-54．

[8]VAN MILL J．The infinite-Dimensional Topology of Function Spaces[M]．Amsterdam：North-Holland Publishing Co．2001．