一类具分布时滞的三阶非线性泛函微分方程的振动性和渐近性

林文贤

（韩山师范学院 数学与统计学院，广东 潮州 521041）

容易知道，作为简谐振荡的数学模型，二阶常微分方程的所有解都有任意大的零点，从而是振动的.而一般地，描述机械、电子振荡的数学模型是泛函微分方程，其振动性和渐近性研究在理论和实际中都有着重要意义，并已取得不少成果[1-18].本文将考虑如下的一类具分布滞量的三阶非线性泛函微分方程

其中α 是奇整数之商，t0＞0．本文总假设下列条件成立：

（H1） r1(t),r2(t)∈C(I,R+)，I=[t0,+∞),R+=[0,+∞)，且

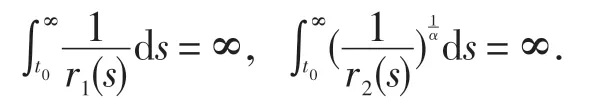
（H2） q(t,ξ)∈C(I×[a,b],R+)；

（H3） g(t,ξ)∈C(I×[a,b],R+);g(t,ξ)分别关于t,ξ 非减，并且

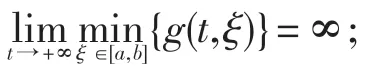
如果函数x(t)∈C1(Tx,+∞),Tx≥t0，使得r2(t)[(r1(t)x′(t))′]α∈C1(Tx,+∞)且在(Tx,+∞)上满足方程（1），则称x(t)为方程（1）的一个解.本文仅考虑方程（1）满足sup{|x(t)|:t ≥T}＞0 对一切T ≥Tx成立的解.方程（1）的解称为振动的，如果它在（Tx,∞）上有任意大的零点.否则，称它为非振动的.

近年来，三阶泛函微分方程的振动性日益受到重视.方程（1）的以下特例在文献中被考虑：

文献[19]给出了方程（2）的解的渐近性，文献[20]利用积分平均方法给出了半线性常微分方程（3）的一切解振动或者收敛于零的充分条件.文献[21]建立了方程（4）的一切解振动或者收敛于零的比较结果.文献[22]在g(t)=t-σ 条件下，利用积分平均方法建立了方程（4）的振动结果.文献[23-25]分别用比较方法证明方程（5）的振动结果.文献[26]利用广义Riccati变换给出方程（6）的一切解振动或者收敛于零的充分条件.本文目的是首先在分析具分布滞量的方程（1）解的结构基础上，利用广义Riccati变换和Hardy-Littlewood-Polya不等式方法，给出方程（1）的一切解振动，或者收敛于零的若干新的充分条件，所得结果推广和改进了文献[20]、[22]和[26]中的相应结果.

引理1 设x(t)是方程（1）的最终正解，则x(t)只有下列两种可能，即存在T ≥t0，使得当t ≥T时有

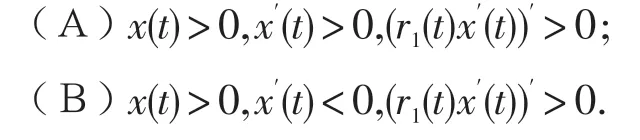
证明 设x(t)是方程（1）的最终正解，且

因 此， r2(t)[(r1(t)x′(t))′]α是 减 函 数，且 最 终 定 号，所 以 有 两 种 可 能，即(r1(t)x′(t))′＜0 或(r1(t)x′(t))′＞0,t ≥t1.如果y″(t)＜0，则存在常数M1＞0使得

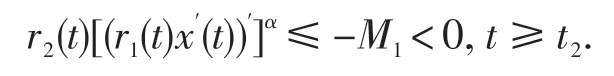
在(t2,t)上对上式积分有

上式中令t →∞，利用（H1），有r1(t)x′(t)→-∞，因此，r1(t)x′(t)最终为负.

于是，存在常数M2＞0使得

在[t3,t)上对上式积分有

上式中令t →∞，利用（H1），有x(t)→-∞，此与x(t)＞0的假设矛盾，故有(r1(t)x′(t))′＞0.因此，x(t)只能有（A）和（B）两种类型，引理1证毕.

为简单计，对充分大的T ≥t0，记

引理2 设x(t)是方程（1）的最终正解，且x(t)具有性质（A），则

证明 取T ≥t0，使x[g(t,ξ)]＞0,t ≥T,ξ ∈[a,b].利用方程（1）得

则r2(t)[(r1(t)x′(t))′]α在[T,∞)上单减，从而有

因此

引理2证毕.

引理3 设x(t)是方程（1）的最终正解，x(t)具有性质（B），且

证明 设x(t)是方程（1）的最终正解，因为x(t)具有性质（B），所以存在有限极限

可以断言l=0.事实上，如果l ＞0，则

积分方程（1）得到

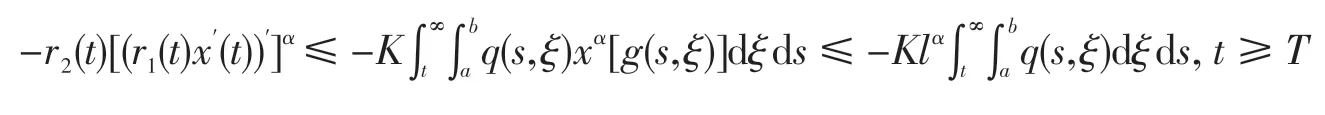
因此

从t到∞积分上面不等式，有

对上式从T到t积分，得到

引理4[27]设X和Y为非负常数，则

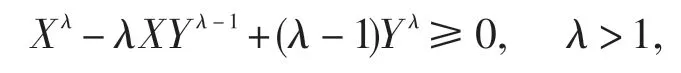
且等式成立当且仅当X=Y

下面利用Philos 型的积分平均技巧[28]，得出方程（1）的新的振动定理.为此引进如下一类函数℘.令

函数H(t,s)∈C(D,R)称为属于℘类，记作H ∈℘，如果

（i）H(t,t)=0,t ≥t0;H(t,s)＞0,(t,s)∈D0;

定理1 设式（7）成立，且g(t,a)≥t，若存在函数

使得

当T0∈[t0,∞)，有

如果存在一个连续函数Ψ:[t0,∞)→R,使得

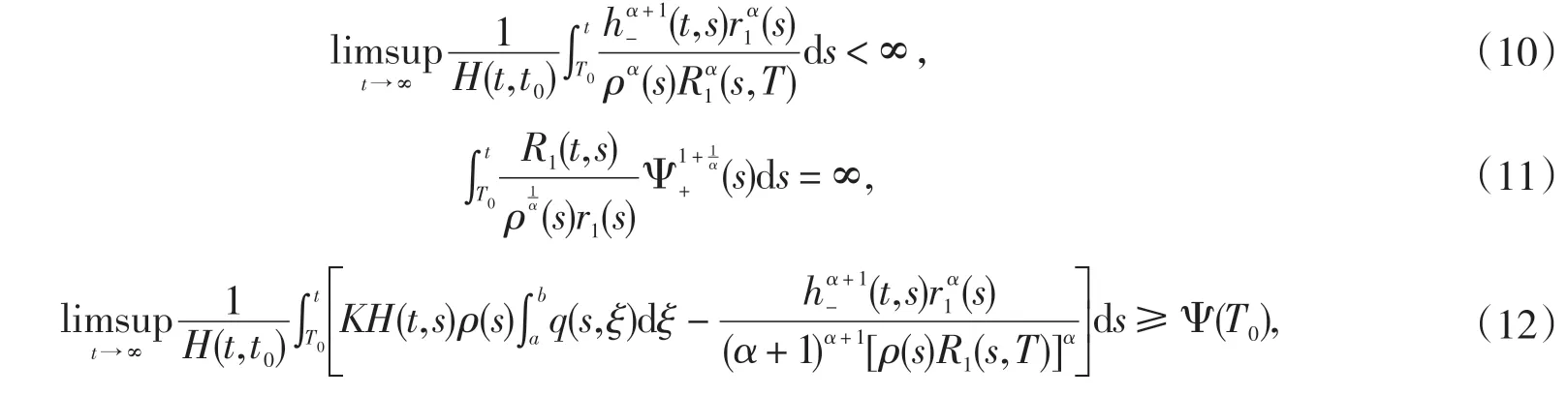
其中

证明 设方程（1）存在非振动解x(t)，不妨设x(t)最终为正解.由引理1 知，x(t)有（A）和（B）两种类型.

（i）设x(t)为(A)型，则有x′(t)＞0,t ≥T.考虑广义Riccati变换

则

因此，利用W(t)的定义，便可得到

在（13）中用s代替t，两边同乘以H(t,s)后，关于s从T0≥T到t ≥T0积分，得

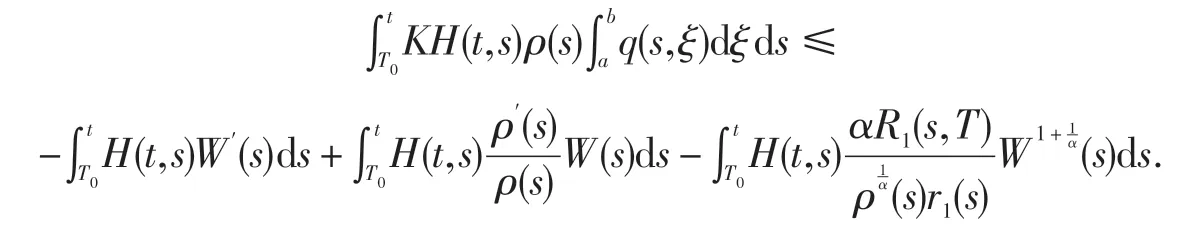
对上述分部积分，利用式（8）产生

定义X ≥0和Y ≥0如下：

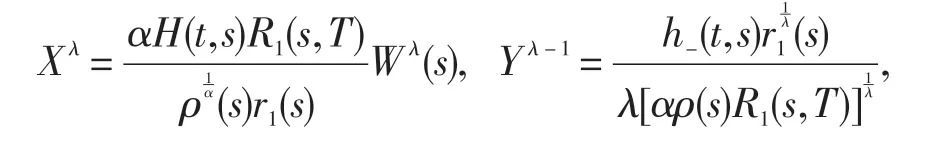
由（14）和（15）便可得到

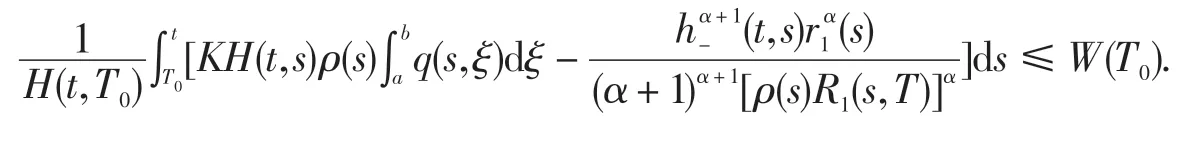
由式（12）得

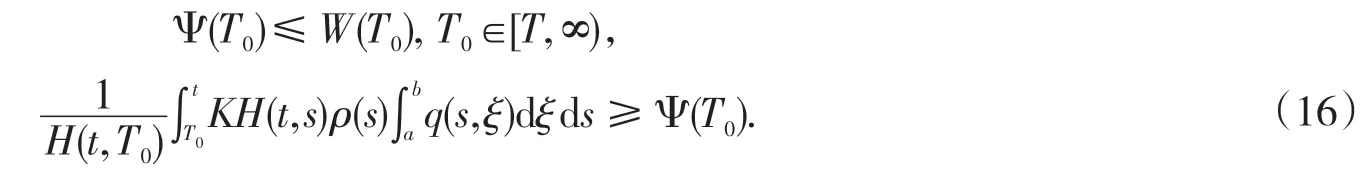
由式（14）得

在上面的不等式中，记

同时注意到（16），可以得到

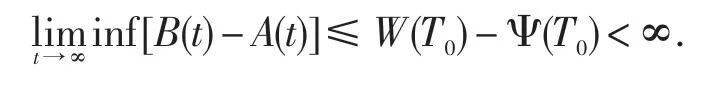
下面用反证法证明

若不然

由式（9）知，存在一个常数ε ＞0，使得

对于任意的实数M ＞0，由（18）知，存在T1∈[T0,∞)，使得当t ∈[T1,∞)时，有

由分部积分公式得

由（19）知，存在T2∈[T1,∞)，使得当t ∈[T2,∞)时，有

所以B(t)≥M.由M 的任意性知

进而选取序列

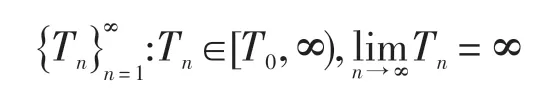
满足

则存在常数M0＞0，使得对于所有充分大的正整数n，有

由（20）容易得到

再由（21）得

由（21）和（22）知，对于充分大的正整数n，下面不等式成立

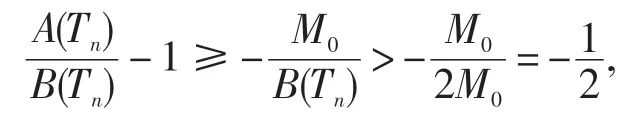
即

因此，由（23）得

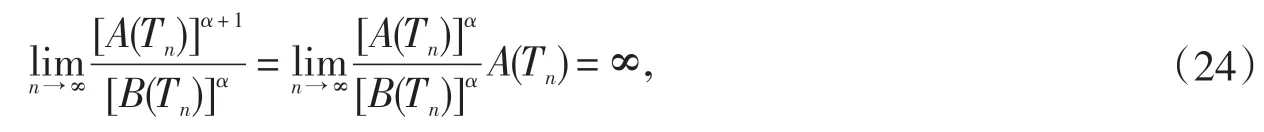
另一方面，应用积分不等式可得

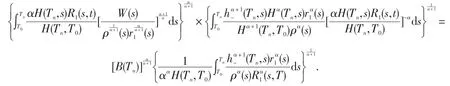
由上式便可得到

于是，由（24）得

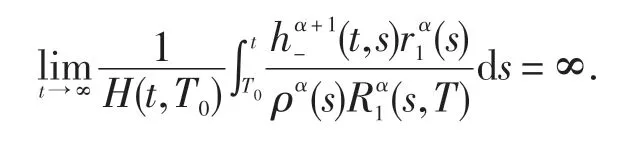
这与式（10）矛盾，从而证得（17）成立.注意到当T0∈[T,∞)时,

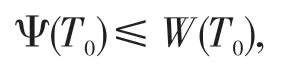
由（17）得

这与式（11）矛盾.

（ii）设x(t)为(B)型，由于（7）成立，故满足引理3的条件，则定理1证毕.

定理2 设式（7）～（9），（11）成立，且g(t,a)≥t，其中H,h,ρ和Ψ如定理1所述.如果

并且

其中

证明 设方程（1）存在非振动解x(t)，不妨设x(t)最终为正解.由引理1 知，x(t)有（A）和（B）两种类型.

（i）设x(t)为(A)型，则有x′(t)＞0,t ≥T.考虑广义Riccati变换

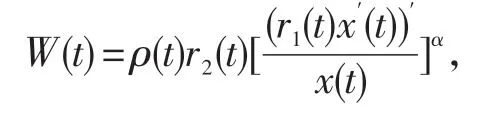
如同定理1的证明，（14）和（15）成立，因此

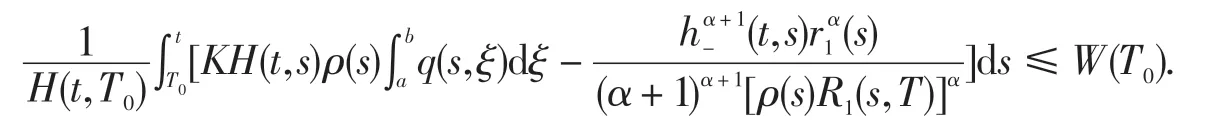
由式（26）得到下面各式成立：

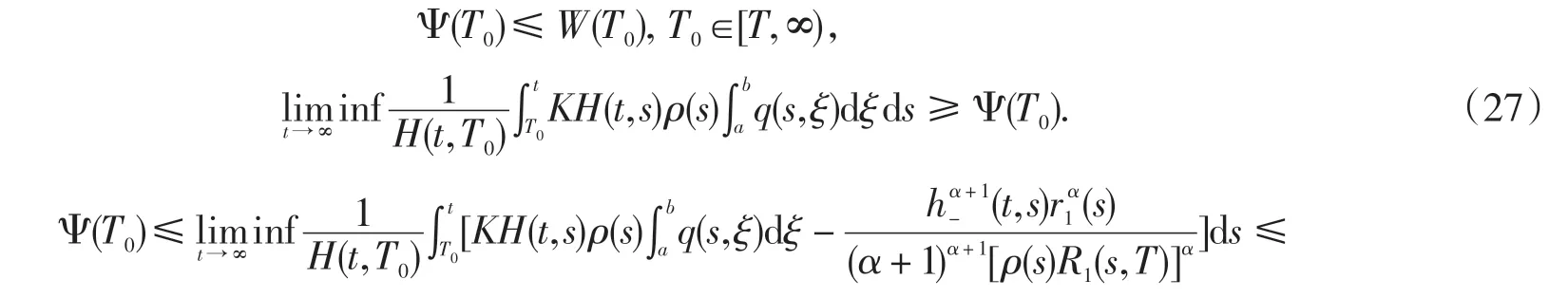
在上式中，由式（25），便可得到

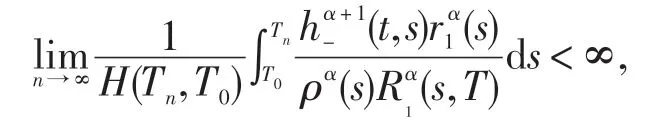
定义A(t)和B(t)如同定理1所述，且与定理1的证明过程类似，由（14）并注意到（27），可得

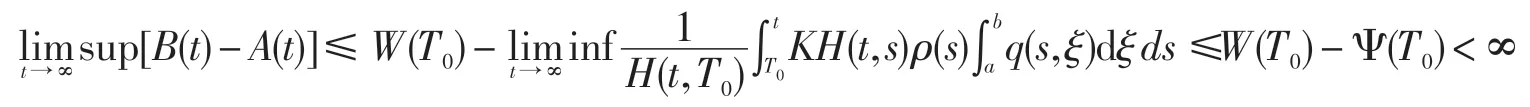
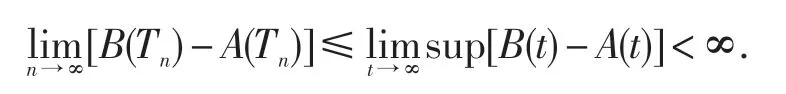
以下用反证法证明式（17）成立.余下的证明与定理1的证明类似，故省略.定理2证毕.

注 若在定理1 和定理2 中，选取不同的函数ρ(t)和H(t,s)，可以得到方程（1）的不同的振动准则.

[1]林文贤.具连续分布滞量的二阶中立型方程的振动性定理[J].应用泛函分析学报，2003，5（2）：174-177.

[2]林文贤.一类非线性偶数阶中立型方程的振动准则[J].工程数学学报，2005，22（1）：159-162.

[3]林文贤.一类中立型泛函微分方程的振动准则[J]，数学的实践与认识，2005，35（6），211-215.

[4]林文贤.一类具连续分布滞量的偶数阶微分方程的新振动性定理[J]，辽宁师范大学学报：自然科学版，2006，29（4），394-396.

[5]林文贤.一类具连续偏差变元的二阶非线性中立型方程的振动性[J].西南师范大学学报：自然科学版，2009，34（4）：1-3.

[6]LIN Wenxian.Interval oscillation theorems for certain second order neutral differential equations with continuous deviating arguments[J].Southeast Asian Bulletin of Mathematics，2010，34（6）：1055-1061.

[7]林文贤.具有阻尼项的中立型Emden-Fowler方程的区间振动准则[J].韩山师范学院学报，2011，32（6）：8-11.

[8]LIN Wenxian.A note on oscillation of certain second order partial functional differential equation with damping [J].Pioneer Journal of Mathematics and Mathematics Sciences，2012，4（1）：125-128.

[9]林文贤.具连续分布时滞的二阶半线性中立型阻尼泛函微分方程的Philos 型振动定理[J].韩山师范学院学报，2012，33（3）：7-12.

[10]林文贤.一类二阶中立型微分不等式最终正解的不存在性[J].河南师范大学学报：自然科学版，2012，40（2）：31-33.

[11]林文贤.二阶中立型阻尼微分不等式最终正解不存在性[J].兰州理工大学学报，2012，38（5）：138-140.

[12]林文贤.具连续偏差变元的二阶阻尼微分方程的振动性[J].中国科学院研究生院学报，2012，29（5）：594-598.

[13]林文贤.一类具阻尼项和连续分布滞量的偶数阶中立型方程的振动性[J].西南师范大学学报：自然科学版，2012，37（9）：1-3.

[14]LIN Wenxian.Oscillation theorems for certain higher order neutral equations with continuous distributed deviating arguments[J].Southeast Asian Bulletin of Mathematics，2012，34（4）：849-854.

[15]林文贤.一类中立型阻尼泛函微分方程的振动性[J].四川师范大学学报：自然科学版，2013，36（3）：20-22.

[16]林文贤.一类三阶中立型阻尼方程的Philos型振动定理[J].宁夏大学学报：自然科学版，2014，35（2）：1-4.

[17]林文贤.一类带强迫项的二阶阻尼微分方程的区间振动性[J].郑州大学学报：理科版，2014，46（2）：1-5.

[18]林文贤，俞元洪.高阶中立型时滞微分方程的振动准则[J].应用数学学报，2014，37（6）：1018-1024.

[19]PARHI N, PADHI S.Asymptotic behavior of solutions of third order nonlinear deay differential equations[J].Indian J Pure Appl Math，2002，33（10）：1609-1620.

[20]BACULIKOVA B,ELABBASY E M,SAKER S H,et a1.Oscillation criteria for third order nonlinear differential equations[J].Math Slovaca，2008，58：201-220.

[21]OJSEJ I.Asymptotic properties of solutions of third order nonlinear differential equations with deviating argument[J].Nonlinear Anal，2008，68：3581-3591.

[22]SAKER S H.Oscillation criteria of third order nonlinear delay differential equations[J].Math Slovaca，2006，56：433-450.

[23]BACULIKOVA B, DZURINA J.Oscillation of third order functional differential equations[J].Electron J Qual Theory Differ Equ，2010，43：1-10.

[24]ACULIKOVA B, DZURINA J.Oscillation of third order nonlinear differential equations[J].Appl Math.Lett，2011，24：466-470.

[25]RACE S R, AGARWAL R P, PAVANI R, et a1.On the oscillation of certain third order nonlinear functional differential equations[J].Appl Math Comput，2008，202：102-1 12.

[26]高丽,张全信.三阶非线性泛函微分方程的振动性和渐近性[J].滨州学院学报,2013,29（6）：1-8.

[27]HARDY G H,LITTERWOOD J E,POLYA G.Inequalities[M].2nd Edition.Cambridge：Cambridge University Press,1952.

[28]Ch G Philos.Oscillation theorems for linear differential equation of second order[J].Arch Math.，1989，53（3）：483-492.