双闭环直流调速系统的时间最优控制

李丽丽，徐文尚

（山东科技大学 电气与自动化工程学院，青岛 266590）

0 引言

随着现代工业的发展，以直流电机为基础的双闭环调速系统得到了广泛应用。传统的双闭环PID控制器结构简单、稳定性好，但它存在一些缺点，比如难以自适应调速系统参数的变化、对系统的非线性参数存在控制误差、必定会产生转速超调等。针对上述缺点，国内许多学者一致致力于采用各种现代控制理论来设计系统，以便获取更好的调速性能[1～3]。文献[1]提出了一种改进的RBF神经网络PID控制方法，文献[2]提出了一种动态参数设计方法，文献[3]提出了一种基于参数自整定的模糊PID控制方法。而本文则从转速超调方面进行研究，提出了一种基于极小值原理的最优时间控制。

在经典的PI调节方法中，当转速上升到给定值n*时，转速调节器输入偏差为0，而输出却由于积分作用还维持在限幅值u*im，电动机仍在加速，只有当转速出现超调之后，ASR才开始退饱和[4]。这种超调量在一些需要频繁起动、制动的设备中是不希望出现的。而时间最优控制可以在输入未达到给定值之前使其反向，这样既避免了转速超调，又能使电机以最短时间到达给定转速，有很高的实用价值。

1 极小值原理介绍

为了解决控制有约束的工程问题，庞特里亚金提出了并证明了极小值原理，其核心思想为：使泛函J取极小值的最优控制u*(t)满足的必要条件是：即在时间区间[t0,tf]内，对于任意的可容许控制变量

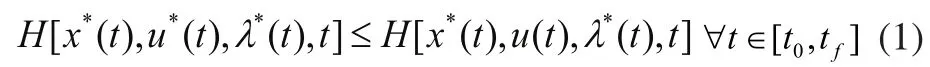
u(t)，都有最优控制u*(t)使得到的哈密顿函数H取极小值[5]。时间最优控制问题，又称为最小时间控制问题，它是极小值原理一个重要的应用，要求在容许控制范围内寻求最优控制，使系统以最短的时间从任意初始状态转移到要求的目标集。对如下正常的线性定常系统[6]：

其最优解的必要条件为：

1）正则方程：

式中，1）哈密顿函数：

2）边界条件：

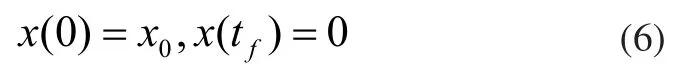
3）极小值条件：

式中，njR b∈ ，为矩阵B的列向量。

4）沿最优轨线H变化律：

2 时间最优控制模型的建立

传统的双闭环直流调速系统模型如图1所示，其中ASR和ACR分别为转速调节器和电流调节器，两者都是带有积分限幅作用的PI调节器。时间最优控制算法的设计思路为：在给定输入与反馈输入的差值小于某一值时，采用传统的双闭环PI调节，当该差值大于设定值，转换为最小时间控制。下面主要介绍下如何将极小值原理应用到双闭环调速系统，建立一个时间最优的控制模型。

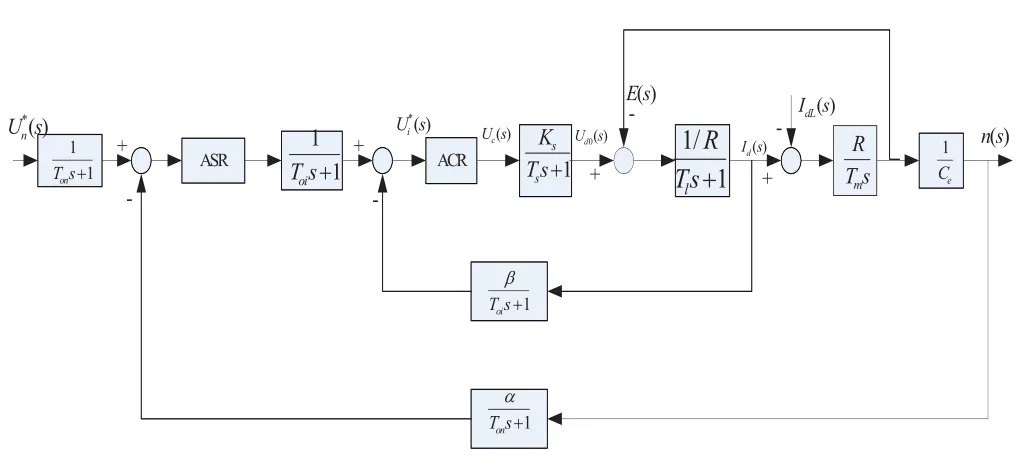
图1 双闭环调速系统动态模型

图2 转速环简化图

则上述偏差系统的状态方程为：

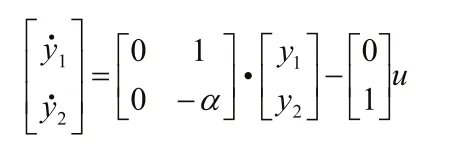
运用极小值原理，寻求最优控制u*，使性能指标最小。

将上述两式综合考虑，得开关线方程：

由开关线方程可以看出，当初始状态在开关轨线的上方时，取u=+1；初始状态在开关轨线下方时，取u=-1。带入原系统状态得最优控制为：

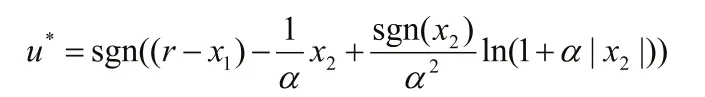
最优控制结构图如图3所示。

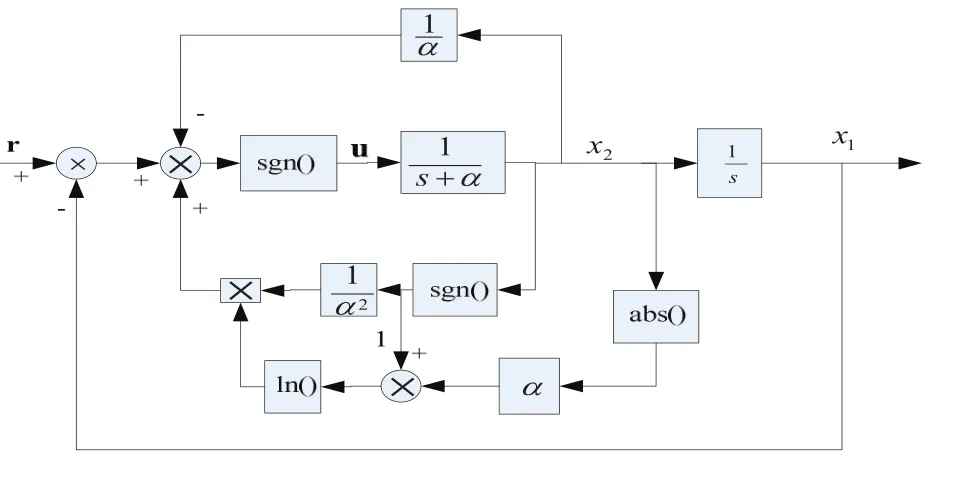
图3 最优控制结构图

至此，时间最优控制系统设计完毕。

3 系统仿真

设有一晶闸管供电的双闭环直流调速系统，参数如下：

直流电动机：220V，136A，1460r/min，Ce=0.132V.min/r，允许过载倍数λ=1.5；晶闸管装置放大系数：Ks=40；电枢回路总电阻：R=0.5Ω5；

时间常数：Tl=0.03s，Tm=0.18s，Tl=0.0017s；

反馈系数：β=0.05V/A，α=0.007V.min/r。

图4所示为Simulink仿真原理图，在仿真模型中设置两个控制回路，一个是传统的双闭环PI控制器，一个是时间最优控制器，通过开关模块Switch进行两种控制器的切换。将Switch的阈值设定为1，即实际转速值与额定转速值相差小于1时，转换为时间最优控制，使转速迅速上升到给定值，避免了转速超调的产生。图5为传统双闭环系统空载起动的仿真结果图，图6为采用了时间最优控制后的空载起动波形图。

图4 双闭环调速系统时间最优控制系统仿真图

4 结论

针对传统的双闭环PI调节器直流调速系统中起动超调过大的问题，采用极小值原理设计出了一个时间最优控制系统，使系统根据设定的阈值自动进行PI调节与最优控制的切换，满足工业生产的需要。由Simulink仿真波形图可以看出，采用时间最优控制的调速系统与传统

图5 传统双闭环系统空载起动波形

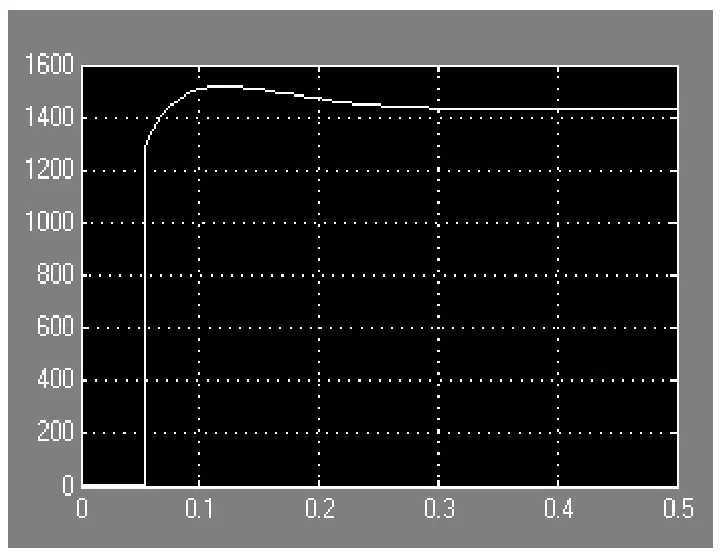
图6 时间最优控制的调速系统控制起动波形

的双闭环调速系统相比，空载起动时转速超调量大大减小，其上升到额定转速的时间也大大加快了，能够满足工程实际的应用。

[1] 郑光,王迆冉.双闭环直流调速系统优化及仿真研究[J].计算机仿真,2013,30(7):321-325.

[2] 李力,余新亮,李骥.直流调速系统PID参数动态设计方法及应用[J].三峡大学学报(自然科学版),2011,33(1):65-68.

[3] 吴燕翔,张朝君,周超群,等.基于参数自整定模糊PID双闭环直流调速系统的设计仿真[J].化工自动化及仪表,2013,40(2):136-139.

[4] 阮毅,陈伯时.电力拖动自动控制系统——运动控制系统(第四版)[M].北京:机械工业出版社,2009.8.

[5] 李传江,马广富.最优控制[M].北京:科学出版社,2011,3.

[6] 胡寿松.自动控制原理(第五版)[M].北京:科学出版社,2007,6.

[7] 李威震,于敬玲.基于MATLAB的双闭环可逆直流调速系统的仿真研究[J].计算机仿真,2004,21(11):42-44.

[8] Juan W Dixon,Ivan A Leal.Current control strategy for brushless DC motors based on a common DC signal[J].IEEE Transaction on Power Electronics,2009,17(2):232-240.

[9] 刘春艳,闻玉凤.基于MATLAB/Simulink双闭环直流调速系统的仿真研究[J].山西大同学报(自然科学版),2014,30(3):26-29.