基于线性分组码的自同步扰码盲识别

张旻，吕全通，朱宇轩

1.电子工程学院网络系，合肥230037 2.安徽省电子制约技术重点实验室，合肥230037 3.清华大学电子工程系，北京100084

基于线性分组码的自同步扰码盲识别

张旻1,2，吕全通1,2，朱宇轩3

1.电子工程学院网络系，合肥230037 2.安徽省电子制约技术重点实验室，合肥230037 3.清华大学电子工程系，北京100084

针对加扰前信息序列为线性分组码情况下的自同步扰码盲识别问题，提出了一种有效的解决方法.首先，从理论上分析了线性分组码与随机序列游程特性的差异，得出了扰码序列正确抽取与错误抽取时输出序列的游程特性的区别；然后，通过遍历寻找抽取后序列的游程比值与随机序列游程比值的欧几里得距离的最大值方式实现了自同步扰码多项式的盲识别.仿真实验验证了理论分析的正确性，解决了0、1均衡情况下的线性分组码自同步扰码盲识别问题，具有一定的工程应用价值.

自同步扰码；盲识别；线性分组码；游程特性；欧几里得距离

扰码作为通信系统的关键技术之一，不仅能提高数据传输同步的准确性，还能使信号频谱弥散从而提高其抗干扰能力［1］.在数字通信系统中，只有对接收的通信信号正确地解扰，才能对后续的信源编码或信道编码数据进行译码分析，进而得到原始信息.在非合作通信领域中，正确有效地识别出扰码的编码参数并完成解扰，是未知信息继续分析处理的前提条件，直接影响到原始信息的正确获取［2］.因此，扰码的盲识别研究引起相关领域学者的高度重视［3-8］.

自同步扰码的收发双方不需要严格同步，而且其保密性较同步扰码更强，故广泛应用于通信系统.在实际通信中，信源编码序列普遍具有0、1不均衡性，目前已有的自同步扰码的盲识别算法通常采用加扰前信源编码序列0、1分布的不均衡特性，如文献［2］以比特状态统计概率分布与均匀分布之间的修正平方欧几里得距离作为比特状态不平衡性的衡量准则来实现自同步扰码的盲识别.文献［9］根据自同步扰乱序列反映在方程组上的特征和扰乱前后数据序列的统计不均衡特性，利用Walsh-Hadamard变换解含错方程组来恢复生成多项式.文献［10］基于信源编码序列不均衡，根据产生的扰码序列与原始扰码序列的相关度判断自同步扰码的生成多项式.文献［11］在对信源不平衡条件下的自同步扰码序列的重码统计特性深入分析的基础上，提出了一种优于Walsh变换法的自同步扰码多项式识别算法.文献［12］分析了信源0、1分布不均衡下的自同步扰码序列的游程统计结果与扰码多项式阶数的关系，实现了对同步扰码多项式阶数的估计.在实际通信系统中，还存在着信道编码后进行加扰的情况，由于信道编码后序列的不均衡度非常小甚至趋近于0，现有的基于序列0、1分布不均衡的算法难以识别此类扰码［5］.文献［5］利用信道编码的校验矩阵对扰码序列进行预处理，通过二元假设检验的方法识别扰码参数，但需要加扰前线性分组码的校验矩阵的先验知识，离全盲识别的要求还有一定差距.

本文针对自同步扰码的输入为线性分组码的情况，提出了一种基于游程比值欧几里得距离的自同步扰码盲识别方法，通过遍历多项式抽取扰码序列，则抽取后的序列游程比值与随机序列游程比值的欧几里得距离最大的一组对应的多项式即为待识别扰码多项式.

1　自同步扰码原理

自同步扰码的加扰以线性反馈移位寄存器（linear feedback shift register，LFSR）为基础［13］，其加扰器的结构如图1所示.扰码序列zk的产生是由信息序列xk和LFSR的输出序列yk共同决定的，其加扰过程可以表示为

式中，ci为LFSR的反馈系数，ci∈｛0，1｝，0＜i＜L且c0=cL=1；⊕表示模二加；Σ表示模二累加.

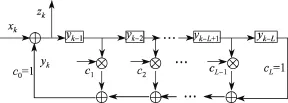
图1　自同步扰码器结构Figure 1 Structure of self-synchronized scrambler

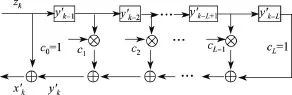
图2　自同步解扰器结构Figure 2 Structure of self-synchronized descrambler

从自同步扰码的结构来看，该结构下的解扰器不需要建立同步；从解扰过程来看，解扰输出的信息序列只与输入的扰码序列zk有关.自同步扰码的加、解扰器只需要相同的LFSR反馈多项式而不需要相同的LFSR初态，即可实现对数据的加扰和解扰.因此，自同步扰码的盲识别问题就是根据截获的扰码序列zk识别出LFSR的多项式.

2　基于线性分组码的自同步扰码参数识别

2.1识别原理

2.1.1游程特性分析

定义1设a是GF（2）上周期为T的周期序列，将a的一个周期a=（a0，a1，a2，···，aT-1）依次按循环排列，使aT-1与a0相邻，则把如100···001和011···110的一连串两两相邻的项分别称为a的一个周期中的一个0游程和1游程.0游程中的0的数目或1游程中1的数目称为这个游程的长［13］.

对于周期为2n-1的m序列，在m序列的一个周期内，共有2n-1个游程，其中0游程和1游程的数目各占一半，长度为m（0＜m 6 n-2）的游程有2n-m-1个［13］.

随着游程长度的递增，m序列的游程数按照1/2规律递减，而且相同游程长度下的0、1游程数基本相等.m序列是伪随机序列，因此随机序列也具有m序列相似的0、1游程分布的特征.

对于（n，k）二元线性分组码而言，k位信息经编码后生成n位码字，构成的集合v（2k）是n维向量空间V（2n）的一个子空间.由k位信息生成的n位线性分组码的码字集合v必定隶属于由n位码字所组成的码字集合V，如图3所示.（n，k）编码有2n-2k个禁用码字，破坏了线性分组码游程的随机特性，导致线性分组码游程的随机性变差.由于线性码的k位信息元可随机产生，长度小于k的游程可以在一个码字中得到，大于等于k的游程只有在两个码字的拼接处才能得到.与随机序列的游程特性相比，线性分组码的游程数在信息位长k的附近发生较大畸变，其游程数不再呈现1/2的递减规律.

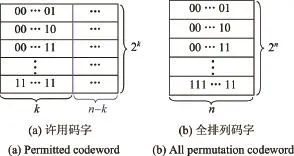
图3　码字分布图Figure 3 Codeword distribution

图4　（6，3）线性分组码码字Figure 4（6，3）linear block codeword

对于图4中的（6，3）线性分组码的编码序列，只有码字011011和码字110110前后拼接时才会出现长度为4的1游程，此种码字组合出现的概率为，因此长度为4的1游程在该编码序列中出现概率为.随机序列不同长度下的0、1游程数是依1/2规律递减的，且相同游程长度下的0、1游程数是相等的［13］，故长度为4的1游程出现概率为.由此可见，两种序列的游程分布有较大差异.

仿真产生序列长度为30 000 bit的（6，3）线性码和随机序列，统计两组序列的游程长度从1～10的游程数，其游程数的分布和相应随机序列游程数的分布如图5和表1所示.

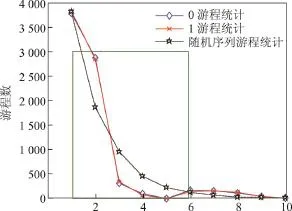
图5　（6，3）线性码游程统计Figure 5（6，3）linear block code's run statistics

（6，3）线性码的游程分布与随机序列游程分布相比有明显的跳跃折点，如图5虚线框中的部分所示.

表1　游程统计结果Table 1 Result of run statistics

根据表1的游程数统计结果，计算（6，3）线性码的游程比值ui和随机序列的游程比值ui（其中ui=vi+1/vi，i=1，2，···，l，i表示游程长度，vi表示长度为i的游程数），统计结果如表2所示.

由表2统计结果可知，（6，3）线性码的游程比值分布与随机序列游程比值分布有较大差异，线性码的0、1游程数不再呈现1/2的递减规律.

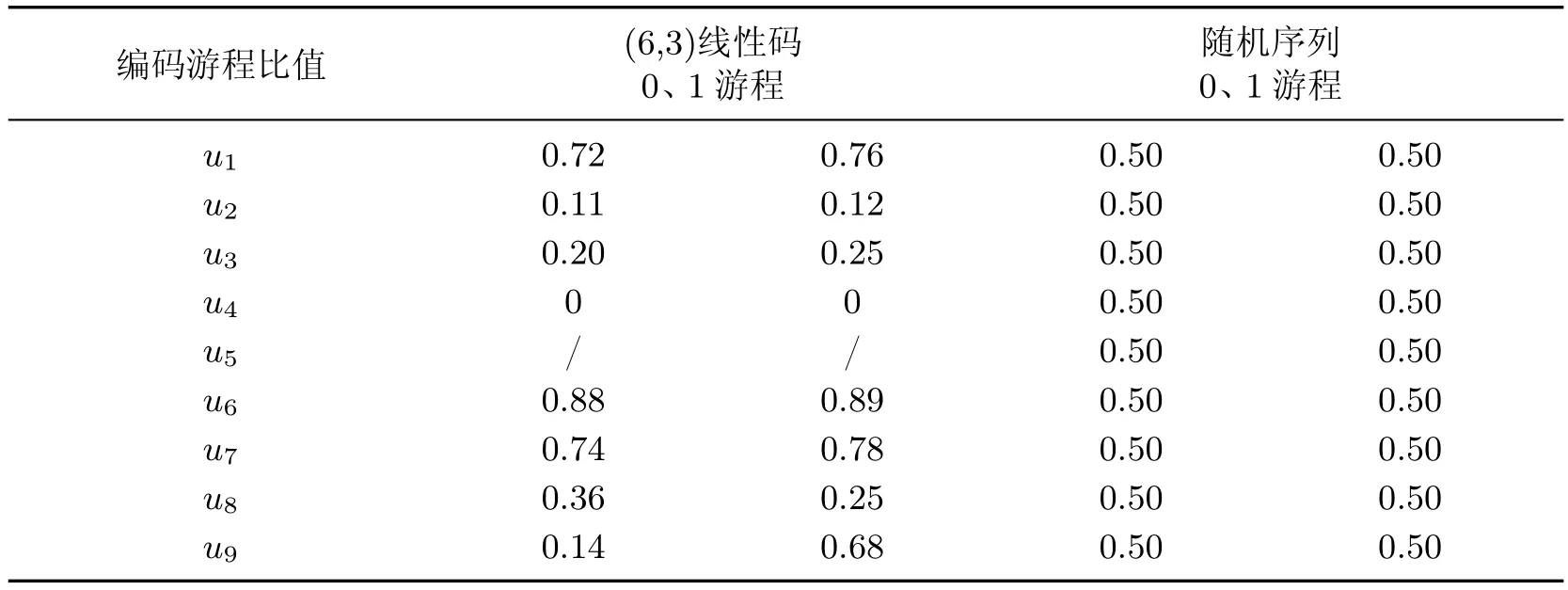
表2　游程比值统计结果Table 2 Result of the run ratio statistics

2.1.2扰码序列的抽取

对于图1所示的自同步扰码器，其生成多项式可以表示为

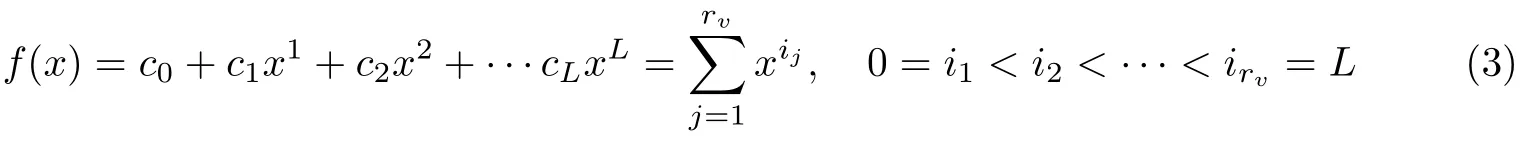
式中，L为LFSR的反馈逻辑输出阶数，rv为生成多项式f（x）的项数

自同步扰码的输入序列为xk，扰码器的输出序列为zk.定义GF（2）上的多项式

按照多项式g（x）对扰码序列抽取并进行模二求和得

1）正确抽取

当g（x）=f（x）时，抽取并模二求和的过程实际上等价于自同步扰码的解扰过程

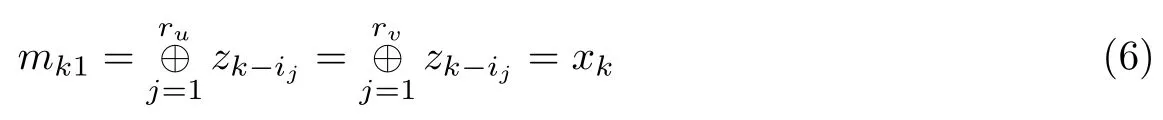
式中，mk1为扰码器的输入序列，即mk1为线性分组编码序列.

2）错误抽取

当g（x）6=f（x）时，式（5）所示的处理过程不是正确的解扰过程.由于扰码序列zk中的0、1等概率出现，错误抽取时抽头位置的0、1比特出现的概率是相等的，其概率为

式中，rw为比特抽取时非生成多项式的项数.

错误抽取时抽头位0、1比特出现的概率是相等的，因此模二求和后的输出序列mk2中的0、1也是等概率出现的，近似为随机序列.

2.2识别准则

由2.1.2节分析可知，正确抽取时的输出序列mk1为线性分组码，而错误抽取时的输出序列mk2为随机序列，因此抽取的输出序列为线性分组码时对应的多项式即为待识别扰码多项式，此时游程数的比值与随机序列游程数的比值相比较分布最不均衡.游程比值分布的不均衡性可用几何距离来衡量，如用欧几里得距离衡量抽取序列与随机序列的游程比值的距离为

式中，Pi为抽取序列的游程比值，Qi=1/2（i=1，2，···，l）为随机序列游程比值，d为0、1游程比值的欧几里得距离之和.

d越大表征抽取序列的游程比值分布与随机序列游程比值分布的距离越远，即游程比值分布越不均衡.当抽取选取的多项式恰好为扰码的生成多项式时，游程比值分布的距离取得最大值.因此，待识别扰码多项式为

式中，G为需要遍历的多项式集合，t为集合G中多项式序号，s为最大欧几里得距离对应的多项式序号.

2.3识别步骤

根据2.1和2.2节的分析，提出了以下的识别步骤：

步骤1对于截获的扰码序列，按照式（5）遍历多项式对扰码序列抽取并模二求和，其输出序列为mk；

步骤2统计输出序列mk的游程数（i表示游程长度，j表示0、1游程），并计算其0、1游程数的前后比值，其中j=0，1，i=1，2，···，l；

步骤3统计每个多项式对应的抽取序列与随机序列的游程比值的欧几里得距离

步骤4最大欧几里得距离对应的多项式即为待识别扰码多项式

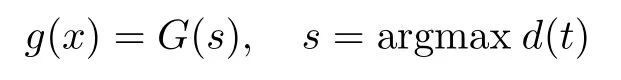
3　仿真实验及性能比较

3.1仿真实验

实际通信中扰码使用的LFSR阶数绝大多数分布在3～60之间，通常采用二项式或三项式，比如ITU V.34中使用的就是三项式1+x18+x23.为给出较为实际有效的正确识别率，遍历多项式时采用三组多项式作为自同步扰码的生成多项式：第1组，由3～60阶的全部58个二项式f（x）=1+xL，L=3，4，···，60组成；第2组，由3～60阶的全部1 769个三项式f（x）=1+xk+xL，L=3，···，60，k=1，···L-1组成；第3组，由3～60阶的五项式组成.由于3～60阶的五项式的总数过于庞大，在各个阶数对应的五项式中分别随机抽取10个或11个多项式，若相应阶数的五项式不足10个（比如3～6阶），则该阶数对应的五项式全部抽取，共555个五项式.多项式集合中共2 382项多项式.

实验中采用ITUV.34中常用的生成多项式为f（x）=1+x18+x23的自同步加扰方式，随机产生长度为45 000 bit的（15，5）线性分组码作信息序列，其序列不均衡度为0，仿真长度为45 000 bit的自同步扰码序列进行盲识别实验，得到的仿真结果如图6所示.

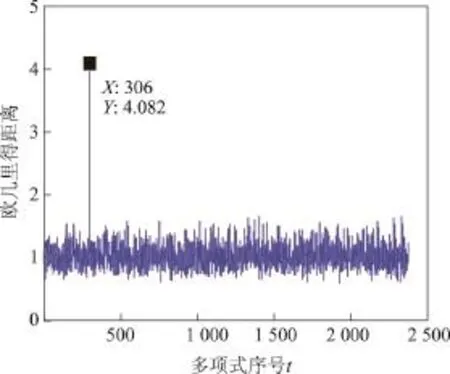
图6　游程欧几里得距离统计Figure 6 Run square Euclidean distance statistics

由图6中的实验结果可以看出，当多项式序号为306（多项式取g（x）=1+x18+x23）时，游程比值的欧几里得距离统计取得最大值，而且与其他多项式对应的游程比值的欧几里得距离有明显差异，由此可判断自同步扰码的生成多项式为g（x）=1+x18+x23，与待识别自同步扰码的多项式一致.因此，通过统计并寻找抽取序列与随机序列游程比值的欧几里得距离最大值的方法，可以有效地实现对自同步扰码多项式的识别.

3.2性能比较

为了更好地说明本文方法的识别性能，将其与文献［2］的方法进行对比实验.仿真对比实验中使用ITU V.34（自同步扰码多项式1+x18+x23）系统中所使用的生成多项式，按照ε=0.01和ε=0.05分别随机生成长度从0～8 000 bit以200 bit步长变化的线性分组码序列作为扰码器的输入信息序列，分别用本文和文献［2］的方法对相应的自同步扰码序列进行蒙特卡罗仿真实验，仿真次数为500次，仿真结果如图7和8所示.

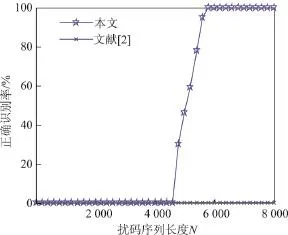
图7　ε=0.01时的识别率Figure 7 Recognition rate of ε=0.01

图8　ε=0.05时的识别率Figure 8 Rcognition rate of ε=0.05

由图7和8的仿真结果可知，本文方法的识别率与不均衡度ε无关，在ε=0.01时也可以实现正确识别.本文方法的识别率与扰码序列长度有关，当数据量为5 800 bit时，正确识别率达到90%以上；当数据量大于6 000 bit时，正确识别率达到100%.文献［2］的方法与不均衡度ε大小关系密切，当ε=0.01时算法失效；但该方法对数据量要求较低，当ε=0.05，且数据量大于2 000 bit时就能准确识别，优于本文方法.

4　结语

本文针对线性分组码不均衡度趋近于0的情况，利用扰码抽取序列游程特性的差异，以抽取序列与随机序列的游程比值欧几里得距离作为判决准则，提出了一种与均衡度无关的自同步扰码识别方法.仿真实验结果表明，本文方法能有效识别不均衡度为0的线性分组码的自同步扰码，且不必已知线性分组码的具体参数，但要遍历多项式，计算量较大，因此下一步的研究还应优化算法以减少计算量.

［1］袁叶.线性扰码的盲识别研究［D］.成都：电子科技大学，2013，6：1-2.

［2］廖红舒，袁叶，甘露.自同步扰码的盲识别方法［J］.通信学报，2013，34（1）：136-143. LIAO H S，YUAN Y，GAN L.Novel blind recognition method for self-synchronized scrambler［J］.Journal on Communications，2013，34（1）：136-143.（in Chinese）

［3］CLUZEAU M.Reconstruction of a linear scrambler［J］.IEEE Transaction on Computers，2007，56（9）：1283-1291.

［4］LIU X B，SOO N K，WU X W，CHUI C C.Reconstructing a linear scrambler with improved detection capability and in the presence of noise［J］.IEEE Transaction on Information Forensics and Security，2012，7（1）：208-218.

［5］LIU X B，SOO N K，WU X W.A study on reconstruction of linear scrambler using dual words of channel encoder［J］.IEEE Transactions on Information Forensics and Security，2013，8（3）：542-552.

［6］郝士琦，戚林，王勇.一种新的伪随机扰码盲识别方法［J］.电路与系统学报，2011，16（4）：6-12. HAO S Q，QI L，WANG Y.A new blind recognition method of pseudo—randomizer code sequence［J］.Journal of Circuits and Systems，2011，16（4）：6-12.（in Chinese）

［7］廖斌，张玉，杨晓静.含错扰码序列生成多项式的快速恢复方法［J］.电子信息对抗技术，2014，29（1）：13-16. LIAO B，ZHANG Y，YANG X J.The method of fast recovery the generate polynomial of interfered scrambling code sequence［J］.Electronic Information Warfare Technology，2014，29（1）：13-16.（in Chinese）

［8］伍文君，黄芝平，唐贵林，刘纯武.含错扰码序列的快速恢复［J］.兵工学报，2009，30（8）：1134-1138. WU W J，HUANG Z P，TANG G L，LIU C W.Fast recovery of interfered scrambling code sequence［J］.Acta Armamentarii，2009，30（8）：1134-1138.（in Chinese）

［9］杨忠立，刘玉君.自同步扰乱序列的综合算法研究［J］.信息技术，2005（2）：30-32. YANG Z L，LIU Y J.Algorithm research of self-synchronizing scrambler sequence［J］.Information Technology，2005（2）：30-32.（in Chinese）

［10］张永光，王挺，楼才义.一种自同步扰码生成多项式的盲识别方法［P］.中国：CN102201912A，2011.

［11］吕喜在，苏绍璟，黄芝平.一种新的自同步扰码多项式盲恢复方法［J］.兵工学报，2011，32（6）：680-685. Lü X Z，SU S J，HUANG Z P.A novel blind recovery method of self-synchronizing scrambling polynomial［J］.Acta Armamentarii，2011，32（6）：680-685.（in Chinese）

［12］黄芝平，周靖，苏绍璟，刘纯武，吕喜在.基于游程统计的自同步扰码多项式阶数估计［J］.电子科技大学学报，2013，42（4）：541-545. HUANG Z P，ZHOU J，SU S J，LIU C W，Lü X Z.Order estimation of self-synchronizing scrambling polynomial based on run statistic［J］.Journal of University of Electronic Science and Technology of China，42（4）：541-545.（in Chinese）

［13］张永光，楼才义.信道编码及其识别分析［M］.北京：电子工业出版社，2010.

（编辑：王雪）

Blind Recognition of Self-Synchronized Scrambler Based on Linear Block Code

ZHANG Min1,2，LÜ Quan-tong1,2，ZHU Yu-xuan3
1.Network Department，Institute of Electronic Engineering，Hefei 230037，China 2.Key Laboratory of Electronic Control technology，Hefei 230037，China 3.Department of Electronic Engineer，Tsinghua University，Beijing 100084，China

A blind recognition method of self-synchronous scrambler based on the linear block code with unbiased information source is proposed.Diferent run characteristics of the linear block code and random sequence are analyzed，leading to the conclusion that the run feature of correctly extracted scrambler sequence difers from that of the wrong one. A polynomial of the scrambler is determined with maximum value search in all possible Euclidean distances between the run ratios of extracted and random sequences.Experiments and simulation results show correctness of the theoretical analysis.Blind recognition of self-synchronous scrambler after the linear block code with unbiased information source can be realized，useful in engineering application.

self-synchronized scrambler，blind recognition，linear block code，run characteristic，Euclidean distance

TP391

0255-8297（2015）02-0178-09

10.3969/j.issn.0255-8297.2015.02.007

2014-09-19；

2014-12-15

国家自然科学基金（No.60972161）资助

张旻，教授，博导，研究方向：智能信息处理、通信信号处理，E-mail：dyzhangmin@163.com