随机激励下掘锚联合机纵向非线性振动特性分析

陈洪月　刘烈北　马　英　张　瑜　谢　苗

1.辽宁工程技术大学，阜新，1230002.国家地方联合矿山液压技术与装备工程研究中心，阜新，1230003.天地科技股份有限公司开采设计事业部，北京，100013

随机激励下掘锚联合机纵向非线性振动特性分析

陈洪月1,2刘烈北1马英3张瑜1谢苗1,2

1.辽宁工程技术大学，阜新，1230002.国家地方联合矿山液压技术与装备工程研究中心，阜新，1230003.天地科技股份有限公司开采设计事业部，北京，100013

将虚拟仿真方法、Bekker模型、Newmark-β法相结合，分析了打顶部锚杆孔时掘锚联合机的非线性振动特性。采用DYNA虚拟仿真获得锚杆钻头的阻力载荷，利用采样定理对载荷进行离散化处理，作为钻头的随机工作载荷；采用Bekker模型描述了掘进机履带与巷道底板间的非线性行为，再根据牛顿运动学定律建立了掘锚联合机多自由度非线性振动方程，利用Newmark-β法对方程进行了求解，分析了整机的振动特性，结果表明：受履带与底板间非线性接触力的影响，整机振动处于混沌态；锚杆钻机工作时，整机虽然存在着俯仰和横滚振动，但振动量很小，整机的竖直振动占主导地位。对掘锚联合机的振动特性进行了现场实验，测量打10组锚杆孔时掘进机本体的振动量，测量结果中有6组的振动量均方根值接近仿真值(1.5 mm)，实验结果表明掘锚联合机的非线性模型在一定程度上可以视为是准确的。

掘锚联合机；非线性的；随机振动；动力学仿真

0　引言

掘锚联合机是煤矿综掘设备的发展方向，国内众多煤机企业[1-2]已经觉察到了该产品的商机，纷纷推出了各具特色的掘锚联合设备，这些设备均以国内应用最为广泛的纵轴式掘进机为载体，在机身或截割臂上安装可移动的单台或两台锚杆钻机，实现巷道的锚杆支护工作。国外方面，因受其巷道的地质条件好、断面宽等因素的影响，掘锚机多以连续采煤机为载体，如奥钢联ABM20、乔伊12BM18，以纵轴掘进机为载体的有英国多斯特LH1400[3]。

为了提高机载锚杆钻机的性能，使锚杆钻机与掘进机有机地结合在一起，在设计过程中，需对锚杆钻机工作时掘锚整机的动态性能进行理论分析，其中文献[4]研究了JMZ型机载锚杆钻机的动力学特性。文献[5]研究了机载单臂式锚杆钻机的力学特性及支护工艺。文献[6]研究了机载锚杆钻机的刚柔耦合力学特性。文献[7]利用虚拟激励法研究了随机激励作用下截割头、悬臂和机体的位移响应特性。文献[8]研究了锚杆钻机工作过程中的最佳姿态。文献[9]研究了钻孔机械手的运动学特性。文献[10]对顶板锚杆钻机的工作过程进行了计算机仿真。在随机振动理论方面，文献[11-18]利用拟广义哈密顿系统的随机平均法、虚拟激励法、复化 Cotes 积分方法、蒙特卡罗模拟法、概率密度演化方法、等效线性法研究了随机激励下非线性模型的振动规律及特点。

以上研究多从掘锚机本身结构方面研究系统的动力学特性，均未考虑掘进机履带与巷道底板间非线性接触力对系统动力学的影响，此外，受锚杆机钻头随机工作载荷的影响，掘锚联合机动力学模型具有随机激励下的非线性振动特性，需采用非线性动力学理论对其进行分析，本文采用虚拟仿真方法获得钻头随机激励，以Bekker模型描述履带与底板间的非线性行为，建立了掘锚机非线性振动模型，并通过实验对模型进行了验证。

1　机载锚杆钻机结构及工作原理

机载锚杆钻机主要由滑道、翻转液压缸、推进液压缸、钻进马达组成。锚杆钻机安装在EBZ160掘进机截割部上盖板的上方，其中滑道与盖板之间通过销轴铰接，钻进马达安装在滑道上。工作时，首先调整掘进机截割臂的位置，使其与巷道顶部之间产生合适的距离，然后在翻转液压缸的驱动下滑道竖起，钻进马达在推进液压缸的驱动下一边沿滑道上升，一边旋转切岩，完成锚杆孔的钻进工作，该机载锚杆钻机具有结构简单、操作简便、实用性强等特点。

2　钻头工作阻力载荷

采用DYNA对钻头钻削煤岩过程进行虚拟实验[6]，截取钻头稳态工作过程中100 s内的阻力载荷，结果如图1所示。以周期为0.01 s对激励进行采样处理，获得了具有10 000个采样点的钻头阻力载荷样本，将该样本作为系统的随机振动激励，样本中最大值为9925 N，最小值为802 N，均方根值为5028 N。

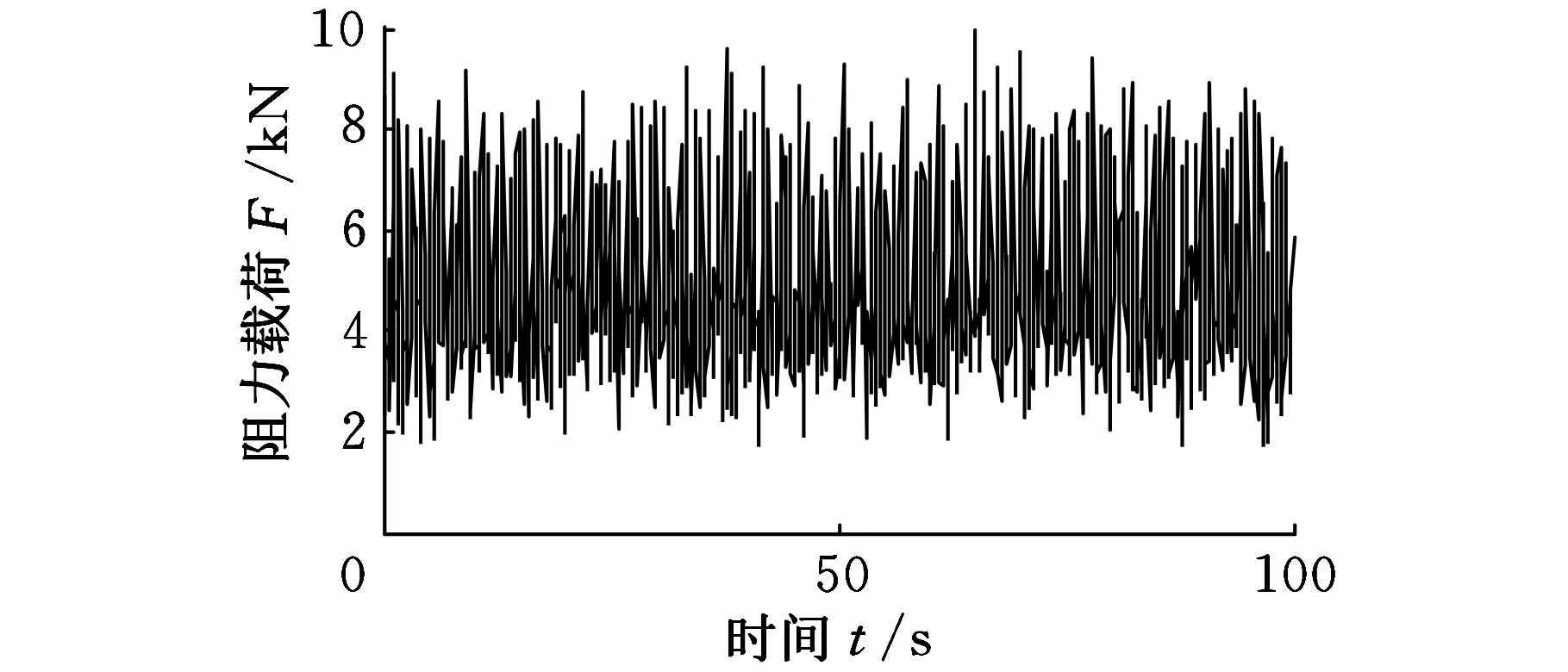
图1　钻头推进阻力载荷

3　履带与巷道底板接触力学模型

由文献[19-20]可知，履带与巷道底板间的接触压力可根据Bekker沉陷理论进行分析，将履带与底板间的接触力集中在履带的两侧驱动轮和导向轮的下端，这时履带上四点的沉陷量xdi与竖直方向的压力pi、土壤内聚力模量kc、内摩擦力模量kφ及变形指数n的关系为

i=1,2,3,4

其中，xdi为履带上四个支撑点的沉陷量；pi为履带的接地压力；Fdi为导向轮、驱动轮处的支撑载荷；L为履带接地面长度(3m)；B为履带接地面宽度(0.60m)；软岩巷道底板的kc为18 170N/mn+2，kφ为1 865 040N/mn+1，n=0.7。令A=(kc/B+kφ)BL/4，则有

4　非线性振动模型的建立

锚杆钻机在打巷道顶部锚杆孔时，钻头的钻进阻力会反向作用到截割臂上，并将力传递到掘进机本体上，使之发生振动，掘进机主要由履带系统中的前方导向轮和后方驱动轮支持在地面上，所以掘进机振动时，除了产生竖直方向上振动外，还会产生俯仰、横滚振动。

根据锚杆钻机工作时掘进机各零部件的运动特征，将掘进机的履带、铲板、主机架、回转台、第一运输机、后支撑部等不动件作为掘进机本体进行分析。系统的坐标原点选取在掘进机本体的重心位置O，如图2所示。其中，m1、x1为掘进机本体的质量和位移，m2、x2为掘进机截割臂的质量和位移，m3、x3为左侧滑道的质量和位移，m4、x4为左侧钻进马达的质量和位移，m5、x5为右侧滑道的质量和位移，m6、x6为右侧钻进马达的质量和位移，J1为掘进机本体俯仰方向的转动惯量，J2为掘进机本体横滚方向的转动惯量，k2、c2为截割臂与掘进机本体间的连接刚度和阻尼，k3、c3为左侧滑道与截割臂间的连接刚度和阻尼，k4、c4为左侧钻进马达与左侧滑道间的连接刚度和阻尼，k5、c5为右侧滑道与截割臂间的连接刚度和阻尼，k6、c6为右侧钻进马达与右侧滑道间的连接刚度和阻尼，a、b为掘进机本体重心距前后支撑点的距离，c、d为掘进机本体重心距左右支撑点的距离，截割臂在本体上的安装位置P与重心O的横纵向距离为e、h。

图2　掘锚联合机非线性振动模型

截割工况下，因掘进机本体的质量较大，所以俯仰角θ和横滚角φ相对较小，这时掘进机本体上四个支撑点处的垂向位移关系可简化为

(1)

截割臂的位移为

xe=x1-e θ+h φ

(2)

对掘锚联合机的各部分进行单独分析，运用牛顿运动学定律，便可建立掘锚联合机多自由度的非线性振动微分方程。令掘进机本体上四个支撑点的支撑力分别为Fd1、Fd2、Fd3、Fd4，则掘进机本体质心处的垂向运动方程为

(3)

本体俯仰运动方程为

(4)

车身横滚运动方程为

(5)

截割臂垂直方向的运动方程为

(6)

左侧滑道和钻进马达垂直方向的运动方程分别为

k3(x3-x2)-k4(x4-x3)=0

(7)

(8)

其中，FL为左侧马达钻进阻力。

右侧滑道和钻进马达垂直方向的运动方程分别为

k5(x5-x2)-k6(x6-x5)=0

(9)

(10)

其中，FR为右侧钻进马达钻进阻力。

将式(1)、式(2)代入式(3)～式(5)，再将式(3)～式(10)整理成矩阵形式，得

(11)

C=

K=

方程中各值可根据EBZ160掘进机和锚杆钻机的结构和设计参数确定，如表1～表4所示。

表1　质量属性

表2　弹性常数估计值

表3　黏性常数估计值

表4　掘锚联合机结构尺寸值

5　模型求解

Newmark-β法是一种逐步积分的方法，当控制参数β=0.5、γ=0.25时，方程是无条件稳定的。由Newmark-β法可知t+Δt时刻的振动微分方程为

F(t+Δt)-f(x)(t+Δt)

对方程求解时，首先根据积分步长Δt、参数β、γ计算积分常数，有

α6=Δt(1-β)α7=βΔt

然后计算有效刚度矩阵：

t+Δt时刻的有效荷载：

t+Δt时刻的位移：

t+Δt时刻的速度和加速度：

6　结果分析

如图3所示：两台锚杆钻机工作时，掘进机本体重心的振动最大值为0.43 mm，最小值为-0.42 mm，均方根为0.15 mm。

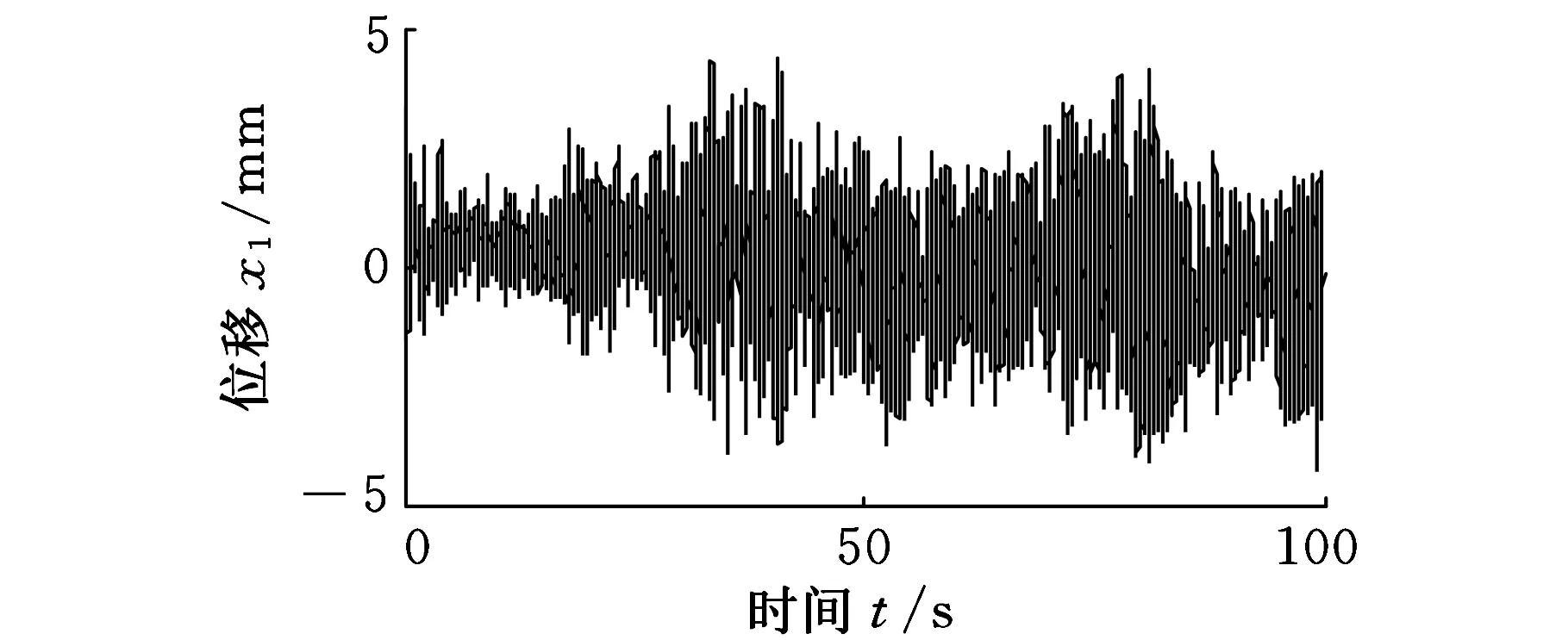
图3　掘进机本体重心的振动位移

由图4可以看出：本体相图轨迹由大量近似的椭圆组成，并且相图轨迹间产生了交叉，图5所示Poincaré 截面中出现多个分散点，说明本体振动存在混沌行为，本体振动极限位置为图4中椭圆左右两侧极点，本体振动最大速度为椭圆的上下极点，为±0.065 m/s。

图4　掘进机本体振动相图

图5　掘进机本体振动Poincaré截面

因掘锚机在低频区域内工作，所以只截取频率在0～200 Hz内系统的幅频曲线，如图6所示。掘进机本体的共振响应频率范围在80～100 Hz、120～140 Hz、170～190 Hz区间内，其中频率为130 Hz时，响应幅值最大，其次为90、185 Hz，锚杆钻机工作频率范围在50 Hz以下，与共振频率存在较大差距。

由图7a可知：掘进机的俯仰振动角均方根值为-0.068 mrad，最大俯仰角达到了-0.2 mrad，说明本体的俯仰振动值很小，根据截割臂安装位置距掘进机本体坐标原点为1600 mm可计算振动偏移量仅为0.005 mm。由图7b可知：当左右两侧锚杆钻机同时工作时，横滚角均方根值为0.018 mrad。

图6　掘进机本体重心幅频曲线

(a)掘进机的俯仰角

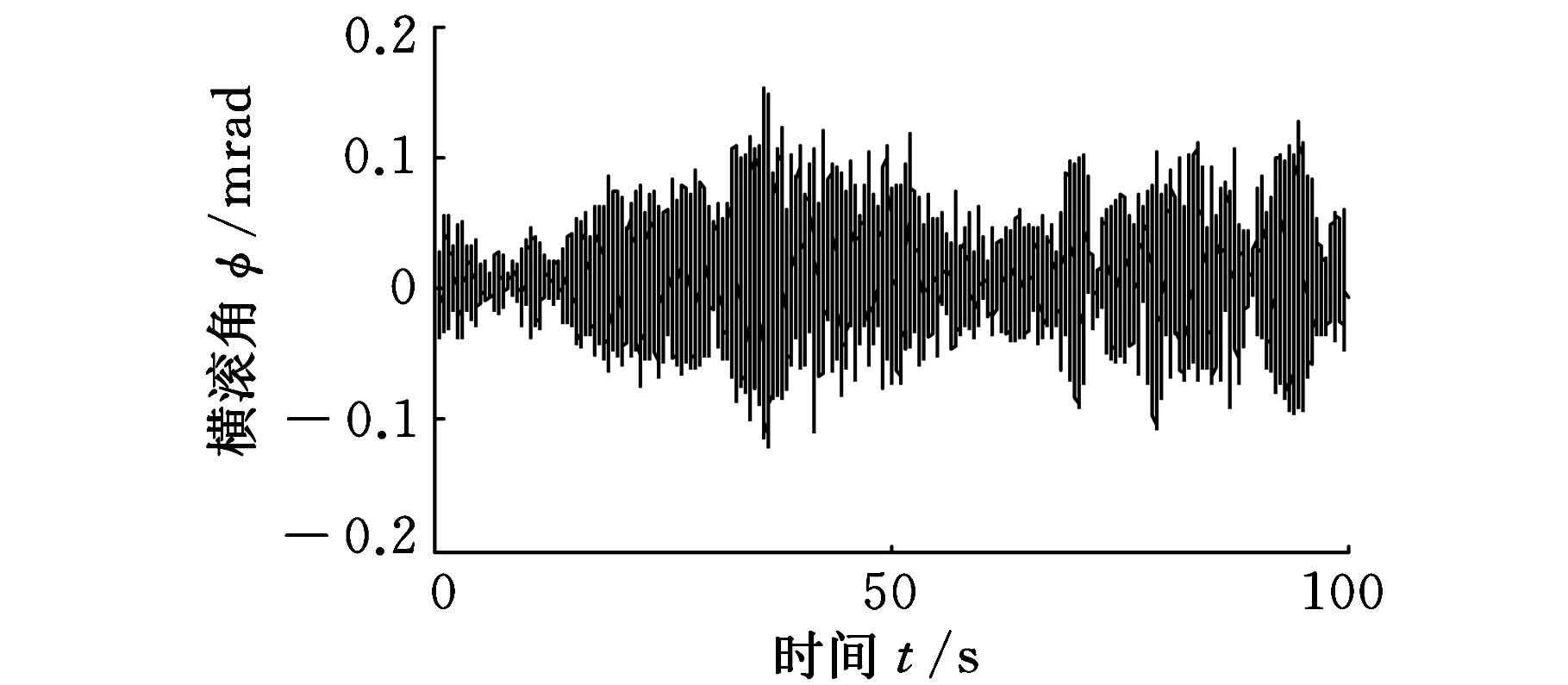
(b)掘进机的横滚角图7　掘进机的俯仰、横滚角

如图8所示：因为左右两侧锚杆钻机的模型参数、激励是相同的，所以两者的振动位移曲线也是相同的，振动量的均方根值为3.2 mm，最大值为5.8 mm，最小值位于振动初始时刻为0，钻头的振动位移全部为正值，这是受掘进机本体振动位移的影响，说明本体振动对钻头的工作精度影响较大，不能被忽视。

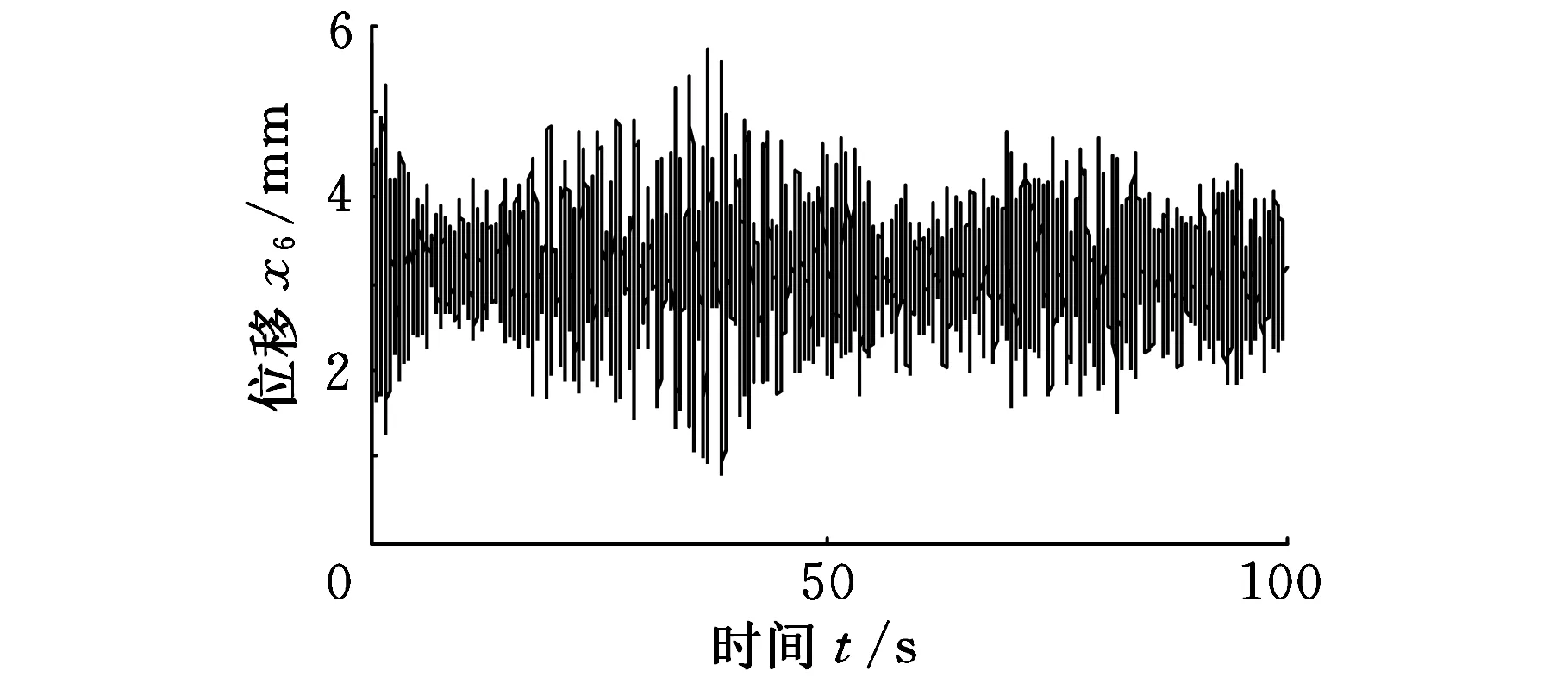
图8　钻头振动位移

7　模型验证

为了验证模型的准确性，对掘锚联合机工况下振动量进行测量：所测试巷道端面为拱形，煤岩硬度d=3，利用锚杆钻机同时打巷道中间的两个锚杆孔，锚杆孔的直径为24 mm，深度为2400 mm。

数据采集：受井下巷道作业及安全条件的限制，不能使用复杂的振动测试仪器对整机的振动特性进行研究，所以采用手持式煤安型振动测试仪对掘锚机的振动量进行测量，为了分析掘进机本体的振动特性，测点选取为掘进机回转台的边缘与掘进机本体中心线的交点处，因为该位置接近于掘进机本体的重心，并且方便测量。

数据处理：分别记录打10组锚杆孔时整机振动量，再从每组截取中间的500个数据点作为样本(图9)，对10组样本的均方根值进行计算，再将其与仿真分析得到的均方根值进行对比，结果如图10所示。

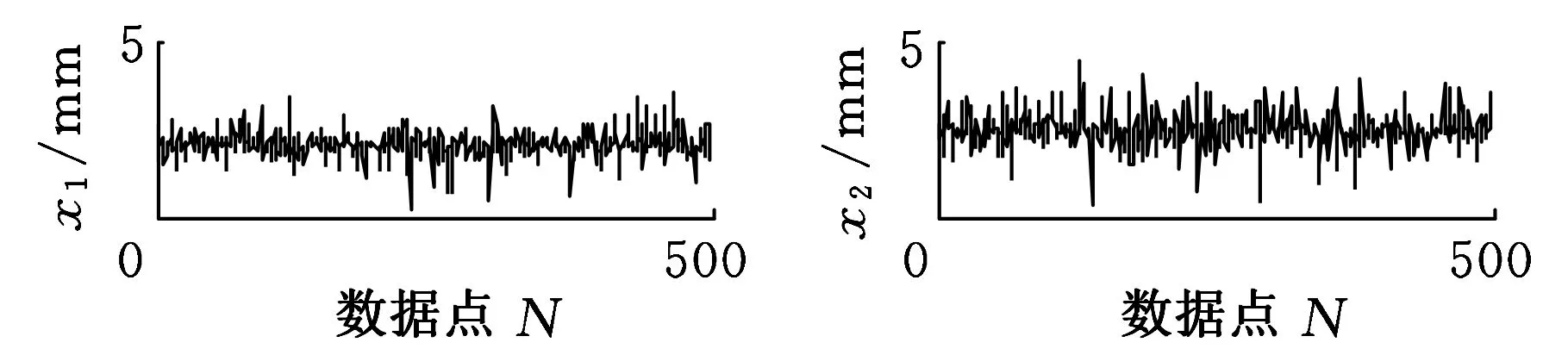
(a)第1组数据(b)第2组数据

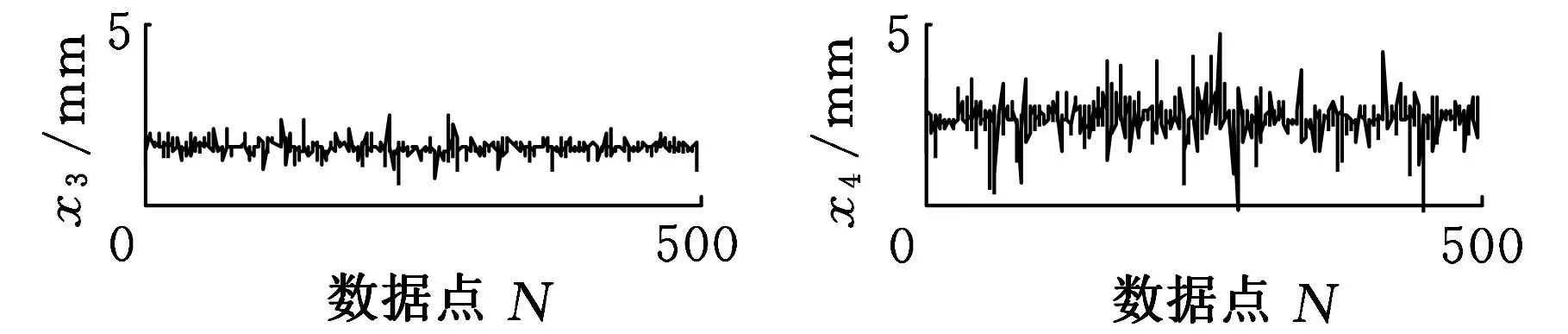
(c)第3组数据(d)第4组数据

(e)第5组数据(f)第6组数据

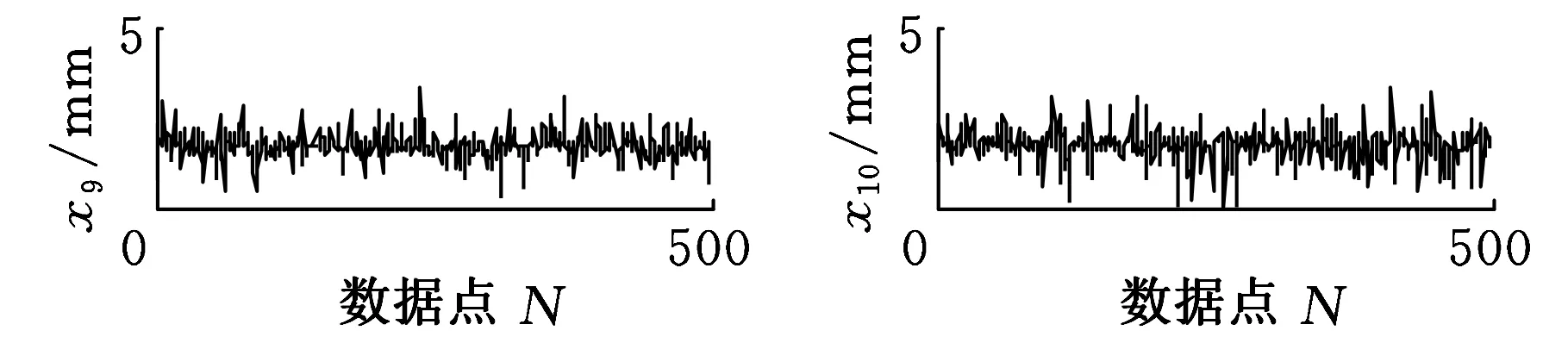
(i)第9组数据(j)第10组数据图9　掘进机本体振动测量值

如图10所示，实际测量得到的均方根值中的最大值为2.68 mm，最小值为1.52 mm，平均值为2.12 mm。对比仿真与实验结果可知：实测值要稍大于仿真值(1.5 mm)。

图10　测量值与理论计算值对比

引起误差的原因有：①实际工作过程中，受煤岩中矸石和煤层节理发育等影响，钻头工作阻力伴随较大的冲击，所以理论分析时钻头载荷加载存在误差；②理论分析时，未考虑掘进机液压动力源所引起的本体振动；③理论分析中各零部件间的刚度和阻尼值为近似值，与实际工况间存在一定的偏差，也会影响计算结果的正确性。

虽然以上原因引起了理论值与测量值之间的误差，但所测10个测量数据点中仍有6个非常接近于理论计算值，这也说明了掘锚联合机的非线性模型在一定程度上可视为正确的，其理论分析结果具有一定的准确性。

8　结论

(1)受掘进机履带与巷道底板间非线性接触力的影响，整机振动处于混沌状态。

(2)锚杆钻机工作时，掘进机本机的振动形态主要为竖直振动，俯仰、横滚振动较弱，可忽略；由振动频响曲线可知：锚杆钻机的工作频率不在掘锚整机的共振频率区域内。

(3)受多种因素的影响，实验测量结果与分析计算结果存在着偏差，但通过实验仍可说明掘锚机非线性振动模型的正确性。

[1]牛宝玉. 采掘锚、掘锚一体化快速掘进成巷技术[J]. 煤炭工程,2003, 50(11): 9-12.

Niu Baoyu. Quick Constructing Roadway Excavation Technology with Mining Anchor Integration of Driving and Bolting[J]. Coal Engineering,2003, 50(11): 9-12.

[2]郭俊生. MB670掘锚机在斜沟井田的快速掘进[J]. 山西焦煤科技,2010(9):12-16.

Guo Junsheng. Rapid Tunneling of MB670Alpine Bolter Miner in Xiegou Field[J].Shanxi Coking Coal Science & Technology,2010(9):12-16.

[3]徐锁庚. 国内外掘猫机组的现状及发展趋势[J].煤矿机械，2006,27(10):3-6.

Xu Suogeng. Present Situation and Development Domestic and Oversea[J]. Coal Mine Machinery,2006,27(10):3-6.

[4]马合群. EZB160掘进机上机载锚杆钻机的动力学特性研究[D]. 淮南：安徽理工大学,2009.

[5]麻勇.机载锚杆钻机伸缩梁力学分析及施工工艺研究[D].西安：西安科技大学,2009.

[6]陈洪月,马英,毛君. 掘进机机载钻孔机械手多体动力学分析[J].煤炭学报,2013,38(8):1484-1490.

Chen Hongyue,Ma Ying,Mao Jun. Multi-body Dynamics Analysis on Drilling Manipulator on Roadheader[J]. Journal of China Coal Society, 2013,38(8):1484-1490.

[7]李晓豁,何洋,李婷,等.纵轴式掘进机横向和纵向随机振动响应的分析[J].煤炭学报,2014,39(3):580-585.

Li Xiaohuo,He Yang,Li Ting,et al. Analysis of Horizontal and Vertical Random Vibration Responses of Longitudinal Roadheader[J]. Journal of China Coal Society,2014,39(3):580-585.

[8]Bucelluni G.Machine Design Parameters for High Seam Truss Bolting Applications[C]//Proceedings Second Conference on Ground Control in Mining.Morgantown, 1982:98-100.

[9]Nam H, Choi W, Ry D,et al.Design of a Bolting Robot for Constructing Steel Structure[C]//ICCAS 2007 - International Conference on Control, Automation and Systems. Seoul, 2007:1946-1949.

[10]Ambrose D H,Bartels J R. Computer Simulations Help Determine Safe Vertical Boom Speeds for Roof Bolting in Underground Coal Mines[J]. J. Safety Res., 2005,36(4):387-397.

[11]朱位秋.随机振动[M]. 北京: 科学出版社，1992.

[12]宋向华,安伟光,蒋运华.任意随机激励下结构随机振动分析的一种数值方法[J]. 振动与冲击,2013,32(12):147-154.

Song Xianghua,An Weiguang,Jiang Yunhua. A Numerical Method for Random Vibration Analysis of Structures under Arbitrary Random Excitations[J]. Journal of Vibration and Shock, 2013,32(12):147-154.

[13]苏成,黄欢,徐瑞,等.大规模非线性系统随机振动显式迭代Monte Carlo模拟法[J]. 振动工程学报,2014，27(2):159-166.

Su Cheng, Huang Huan,Xu Rui.Random Vibration Analysis of Large-scale Nonlinear Systems by Explicit Iteration Monte Carlo Simulation Method[J]. Journal of Vibration Engineering,2014, 27(2):159-166.

[14]彭勇波,李杰. 非线性随机振动分析的概率密度演化方法[J]. 西南交通大学学报,2014,49(2) : 220-226.Peng Yongbo, Li Jie. Probability Density Evolution Method of Nonlinear Random Vibration Analysis[J]．Journal of Southwest Jiaotong University, 2014，49(2): 220-226．

[15]林家浩, 张亚辉.随机振动的虚拟激励法[M].北京: 科学出版社,1992.

[16]魏永祥,陈建军,马洪波. 随机参数齿轮系统的非线性动力响应分析[J]. 工程力学,2012,29(11):319-324.

Wei Yongxiang, Chen Jianjun, Ma Hongbo. Analysis of Nonlinear Dynamic Response of Gear-rotor with Random Parameters[J]. Engineering Mechanics, 2012,29(11):319-324.

[17]Kazuya F, Armen D K.Tail-equivalent Linearization Method for Nonlinear Random Vibration[J]. Probabilistic Engineering Mechanic,2007,1(22):63-76.

[18]胡海岩.应用非线性动力学[M].北京:航空工业出版社,2000.

[19]李军,李强,周靖凯. 软土条件下履带-地面相互作用分析[J]. 兵工学报,2012,32(12):1123-1130.

Li Jun,Li Qiang,Zhou Jingkai. Analysis of Track-terrain Interaction on Soft Soil[J]. Acta Armamentarii, 2012,32(12):1123-1130.

[20]张克健.车辆地面力学[M].北京: 国防工业出版社，2002.

(编辑王艳丽)

Analysis of Vertical Nonlinear Vibration Characteristics for Bolter System on Roadheader under Random Excitation

Chen Hongyue1,2Liu Liebei1Ma Ying3Zhang Yu1Xie Miao1,2

1.Liaoning Technical University,Fuxin,Liaoning,123000 2.National and Local Combined Mining Technology and Equipment Engineering Research Center,Fuxin,Liaoning,123000 3.Coal Mining & Designing Department,Tiandi Science & Technology Co.,Ltd.,Beijing,100013

By combining the virtual simulation method, the Bekker model and the Newmark-β method, the nonlinear vibration characteristics of a bolter system on roadheader was analyzed during the process of drilling the top bolting hole. The resistance load of the anchor bit was obtained by the virtual simulation with DYNA software, and the load was discretized to be the random working load by employing the sample theorem. The nonlinear relation between the roadheader track and the tunnel bottom floor was expressed by Bekker model, and the multi-degree nonlinear vibration equation of the bolter system on roadheader was established according to Newton kinematics law. The equation was resolved by Newmark-β method, and the vibration characteristics of the entire machine was analyzed. The results show that the vibration state of the entire machine is as chaos state by the influence of the contact force between the roadheader track and the tunnel bottom floor, the vibration quantity is very small though the pitch vibration and the roll vibration exist simultaneously, and the vertical vibration of the entire machine is predominant. Field experiments were carried out about vibration characteristics of the roadheader. Amount of vibration of the roadheader were measured when drilling 10 set of bolt holes. The root mean square values in the measured results of 6 set of vibration are close to the simulation value(1.5 mm). Experimental results show that non-linear model of the bolter system on roadheader can be seen as accurate to some extent.

bolter system on roadheader; nonlinear; random vibration; dynamics simulation

2014-10-09

国家自然科学基金资助项目(51304107)

TD421.5DOI：10.3969/j.issn.1004-132X.2015.17.018

陈洪月，男，1982年生。辽宁工程技术大学机械工程学院副教授、博士。主要研究方向为机械系统动态特性。刘烈北，男，1990年生。辽宁工程技术大学机械工程学院硕士研究生。马英，男，1982年生。天地科技股份有限公司开采设计事业部工程师。张瑜，男，1987年生。辽宁工程技术大学机械工程学院博士研究生。谢苗，女，1980年生。辽宁工程技术大学机械工程学院副教授、博士研究生导师。