考虑多目标的工艺规划与调度集成问题研究

李　言　巴　黎　曹　源　刘　永　杨明顺

西安理工大学，西安，710048

考虑多目标的工艺规划与调度集成问题研究

李言巴黎曹源刘永杨明顺

西安理工大学，西安，710048

针对工艺规划与调度集成问题在多目标优化方面的不足，考虑将多目标优化集成到工艺规划与调度集成问题中。以最长完工时间、加工成本及设备最大负载为优化目标，对该多目标工艺规划与调度集成问题进行建模，并提出了一种非支配排序遗传算法，鉴于加工信息的多样性，使用多层结构表示可行解，对该算法的选择及遗传操作等步骤进行了设计。最后，以实例验证了上述模型的正确性及算法的有效性。

工艺规划与调度集成；多目标；非支配排序遗传算法；选择操作

0　引言

工艺规划与调度作为生产系统中极为重要的两个子系统，往往以独立、串行的模式运行[1-3]。在产品设计阶段，工艺规划指定工件从毛坯至成品所需的原材料、机床及加工路线；在调度阶段，调度系统将根据工艺规划获得的结果，对各加工资源进行调度[3]。这种相互独立、串行的运行方式，易导致工艺路线不切合实际、资源利用不均、产生调度瓶颈等问题[1-3]。

近年来，工艺规划与调度集成(integrated process planning and scheduling，IPPS)逐渐成为国内外学者们的研究热点。工艺规划与调度的集成，对于消除资源冲突、减少工件流通时间、提高设备利用率、缩短产品制造周期等具有重要意义[1-2]。

当前，针对IPPS问题的相关研究集中在理论研究、集成模型、算法改进等方面。理论研究方面，文献[1-2]指出了单独考虑工艺规划与调度所导致的多种问题及局限性，介绍了目前解决静态及动态IPPS的多种方法，给出了工艺规划与车间调度以及两者集成研究的发展方向。集成模型方面，文献[3]提出了一种基于代理的IPPS方法，将IPPS问题涉及的工件、机器及求解算法以Agent的形式进行封装，提出了一种基于Agent的IPPS系统；文献[4]提出了一种由初始规划层、匹配规划层及详细规划层组成的三层结构IPPS复合式集成模型，并通过一个应用实例对该模型进行了验证；文献[5]提出了一种由工艺规划选择模块、调度模块、调度分析模块及工艺路线修正模块组成的IPPS模型，提出一种遗传算法对IPPS问题进行了求解。算法改进方面，文献[6]针对IPPS问题，以最长完工时间(makespan)为优化目标，提出一种基于遗传算法和禁忌搜索的混合算法，并以多个算例对该算法进行了验证；文献[7]针对IPPS问题，分别建立了makespan、加工成本等因素的数学优化模型，提出了一种基于进化算法的求解方法，最后，以多个实例对所建模型及算法进行了验证；文献[8]针对以makespan为优化目标的IPPS问题，提出了一种主动学习遗传算法，并以多个实例验证了该算法的有效性；文献[9]针对IPPS问题，使用与或图表示各工件的各道工序以及各工序间的关系，提出了一种改进蚁群算法，并通过大量实例对该算法进行了验证；文献[10]针对IPPS问题，提出一种将遗传算法与人工神经网络结合的混合启发式算法，并以多个算例对该算法进行了验证。

目前，针对IPPS问题进行建模与求解的相关文献，大多以makespan作为优化目标。实际生产中，企业由多个不同职能的部门组成，由于各部门对生产调度的期望有所不同，且各期望目标可能存在相互冲突[11]，若仅以makespan为优化目标，难以符合实际的生产调度情况。

将多目标优化与生产调度问题相结合，形成了多种多目标生产调度问题，如：多目标柔性作业车间调度问题(multi-objective flexible job-shop scheduling problem，MOFJSP)[11-18]、多目标作业车间调度问题(multi-objective job-shop scheduling problem，MOJSP)[19]、多目标流水作业调度问题(multi-objective flow-shop scheduling problem，MOFSP)[20]、多目标并行机调度问题(multi-objective parallel machine scheduling problem，MOPMSP)[21]、多目标开放作业调度问题(multi-objective open shop scheduling problem，MOOSSP)[22]等。

考虑多目标优化的生产调度问题的相关文献大多为作业车间调度(job-shop scheduling problem，JSP)、流水作业调度(flow-shop scheduling problem，FSP)问题。随着制造技术的不断改进与提升，一方面，大多数车间存在多种功能相似的设备共存的状况[23]；另一方面，由于加工手段和技术的多样性，工件已不再拘泥于单一工艺路线[1]。IPPS问题同时具有并行机环境及复合工艺路线特点，相较于JSP、FSP等通常的调度问题，该问题的求解空间更大、复杂度更高，其调度结果也更加符合实际的生产情况，已被认定为NP困难问题[6-7]。

笔者在上述文献的基础上，同时考虑makespan、加工成本及设备最大负载3个优化目标，提出一种多目标IPPS(multi-objective integrated process planning and scheduling，MOIPPS)问题，建立该问题的数学模型，并设计相应的求解算法，最后，以一个实例对模型及算法进行验证。

1　问题建模

基于上述参数，分别以makespan最小、加工成本最小及设备最大负载最小为优化目标，建立目标函数如下。

makespan最小：

(1)

加工成本最低：

(2)

设备最大负载最小：

(3)

针对本文所研究的问题，考虑以下约束：

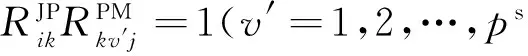
(4)

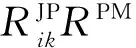
(5)

(6)

根据约束(3)，更新各相关参数如下：

(1)工件i的第v″道工序的完工时间为

(7)

(2)加工设备j的可开工时间为

(8)

(9)

2　算法设计

由上述建模过程可知，MOIPPS问题属NP困难问题。Deb等[24]在2002年提出一种针对多目标优化的非支配排序遗传算法(non-dominated sorting genetic algorithm-Ⅱ，NSGA-Ⅱ)，该算法被广泛用于各种多目标优化问题的求解[19]。

本文提出一种适用于MOIPPS问题的非支配排序遗传算法，由于MOIPPS问题的复杂性及离散性，需要对算法的一些关键模块进行设计。

2.1编码

由于MOIPPS问题加工信息的多样性，为便于后续的遗传操作，本文提出一种6层编码结构，将加工所需的所有信息集成到该结构当中，对调度方案进行编码。该结构由工件层、机器层、加工时间层、加工成本层、加工方法层及工艺路线层组成。其中，工件层为各工件的编码；机器层为各加工设备的编码；加工时间层为机器对应不同工序的加工时间；加工成本层为机器对应不同工序的加工成本；加工方法层为工件各道工序对应的加工方法；工艺路线层为不同工件对应的工艺路线编码。

基于上述定义，以3种工件、3台机器的MOIPPS问题为例，其编码示例如表1所示。

表1　MOIPPS问题编码示例

表1中，第1列的码值表示工件2采用工艺路线4进行加工，由于工件编码2第1次出现在工件层，即代表该工件的第1道工序，其第1道工序的加工方法为2，由机器3加工，加工时间为3.6 h，加工成本为30元/h。以此类推。

2.2解码

采用半主动解码对各解进行解码，假设编码长度为l，具体解码步骤如下：

(1)初始化计数器i=1；

(2)提取当前解的编码中位于第i列上的数据；

(3)若该列对应工件层上的编码值在工件层中第s次出现，则代表该工件的第s道工序；

(4)根据第i列中的数据，以及建模中的约束条件，记录该工件第s道工序对应的加工时间区间；

(5)i←i+1，若i>l，则表示各工件各道工序的加工时间区间已确定，转至步骤(6)；否则，转至步骤(2)；

(6)根据各工件各道工序的加工时间区间，获得makespan及设备最大负载；

(7)根据各工件各道工序的加工时间区间及机器的加工成本，获得该解对应的加工成本。

至此，一次解码操作完毕。

2.3选择操作

本文首先结合Pareto支配关系，对各解进行分层操作，得到各解对应的前沿层级；其次，计算各解的拥挤度；最后，结合偏序关系，使用锦标赛选择法对种群进行选择操作。

2.3.1分层操作

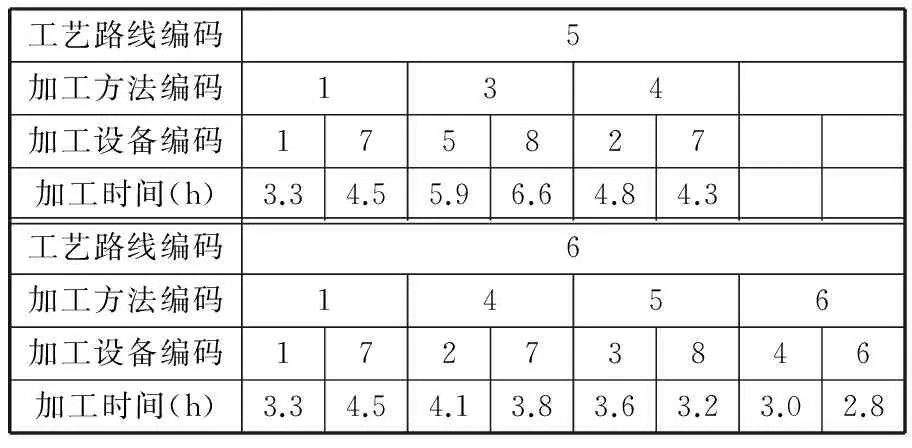
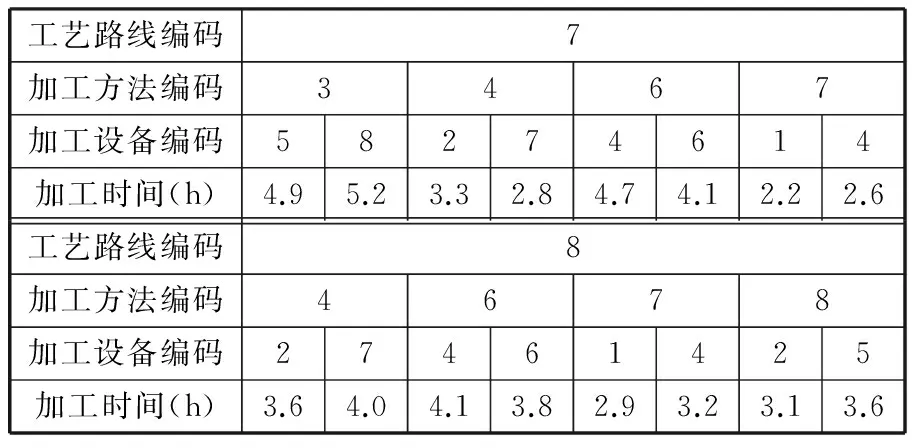
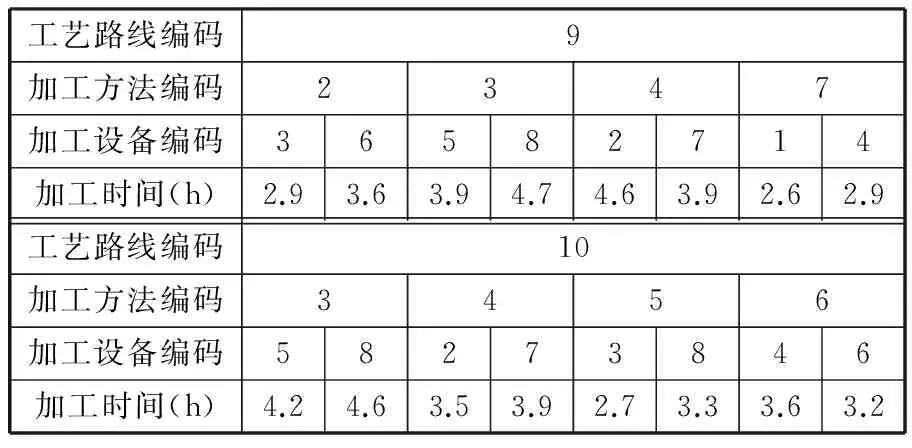
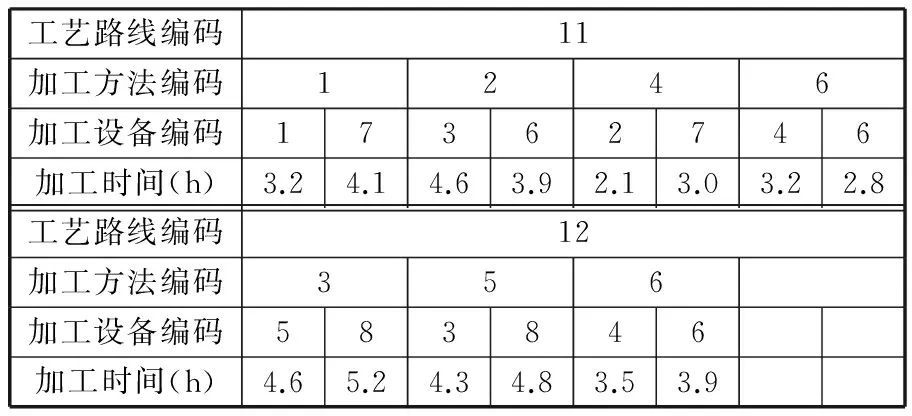
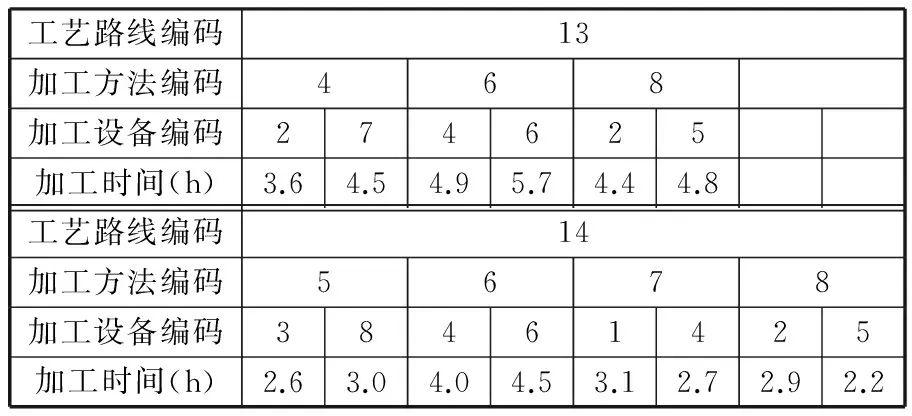
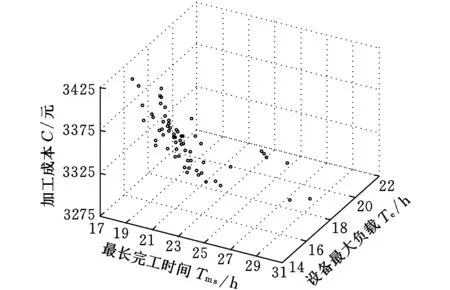
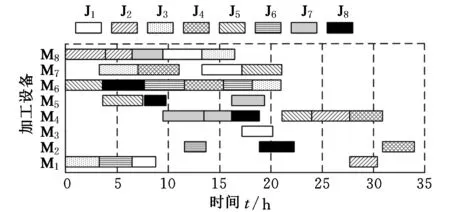
进行分层操作前，首先定义Pareto支配关系[22]：对于具有N个优化目标的多目标最小化问题，假设某解集P由M个个体组成，P={x1，x2，…，xM}，对于任意解xi，对应第j个目标的目标值为fj(xi)，则解xu支配解xv需同时满足以下条件：①对于任意目标值fk，满足fk(xu)≤fk(xv)；②∃k′，满足fk′(xu)

由上述Pareto支配关系的定义可知，对于多目标最小化问题，若解xu支配解xv，则解xu优于解xv。

假设种群P={x1，x2，…，xM}，对应层级集合RANK={rank1，rank2，…，rankM}，被支配数集合DN={dn1，dn2，…，dnM}，初始化rankh=-1，dnh=0，h=1,2,…,M。分层操作步骤如下：

(1)初始化层级计数器w=1；

(2)针对种群P，按照上述Pareto支配关系，确定P中每个个体的被支配数；

(3)对于P中被支配数为0的个体，将w赋值给这些个体对应的层级；

(4)删去P中层级为w的个体，w←w+1，若此时P非空，令剩余个体的被支配数为0，转至步骤(2)，否则，P中所有个体的层级被确定。

2.3.2拥挤度计算

除前沿层级外，拥挤度是比较个体优劣的另一个重要指标。若两个相比较的个体所属层级相同，为保持种群多样性，一般认为拥挤度较大的个体为较优个体[24]。

对于上述最小化问题，假设拥挤度集合CD={cd1，cd2，…，cdM}，则个体xi对应拥挤度cdi的计算按照以下步骤进行：

(1)初始化计数器j=1；

(2)根据种群P中个体对应第j个目标的目标值fj，将种群P中的个体由小到大排列；

(3)若xi排在第1位或末位，置cdi为一个绝对大的数值，跳转至步骤(9)；否则，跳转至步骤(4)；

(4)找到经过排序后，排在xi前一位和后一位的个体，假设分别为xfront、xbehind；

(5)找到对应fj值最大和最小的两个个体，假设分别为xmax、xmin；

(6)计算xi对应第j个目标的拥挤度，即

cdfij=(fj(xbehind)-fj(xfront))/(fj(xmax)-fj(xmin))

(10)

(7)j←j+1，若j>N，跳转至步骤(8)，否则，跳转至步骤(2)；

(8)计算xi的拥挤度，即

(11)

(9)计算结束，得到cdi。

2.3.3锦标赛选择

在进行锦标赛选择前，首先定义偏序关系[24]：对于具有N个优化目标的多目标最小化问题，假设某解集P由M个个体组成，解xu、xv对应的前沿层级分别为ranku、rankv，对应的拥挤度分别为cdu、cdv，定义偏序符号为“”，则xuxv需满足条件rankucdv。u，v=1,2,…,M。

由上述可知，若xuxv，则解xu优于xv。

假设种群规模为M，竞赛个体总数为CN(CN

(1)从种群中随机选择CN个个体；

(2)依照上述偏序关系的定义，从该CN个个体中选出最优个体作为一个预交叉个体；

(3)重新从种群中随机选择CN个个体；

(4)依照上述偏序关系的定义，从该CN个个体中选出最优个体作为另一个预交叉个体。

2.4交叉操作

本文使用POX交叉(precedence operation crossover，POX)对多层编码结构的个体进行交叉。以2种工件、3台机器的MOIPPS问题为例，假设要交叉的工件为工件2，POX交叉如图1所示。

图1　MOIPPS问题的POX交叉操作

由于不同父代中相同工件可能选择不同的工艺路线，可能会出现同一工件在不同父代中工序数不同的情况，因此，交叉后所产生的新个体的编码长度会有所变化，如图1所示。

2.5变异操作

本文采用两种变异方法，一种是依照Swap互换操作概率对某两列编码进行Swap互换操作，另一种是依照机器层单点变异概率对机器层进行单点变异操作。假设个体变异概率为Pm、Swap互换操作概率为Pm1、机器层单点变异概率为Pm2，变异操作的流程图如图2所示。

图2　变异操作流程

由于在进行Swap互换操作后所产生的新解可能出现同一工件的后道工序排在前道工序之前的情况，即产生非法解，因而，在Swap互换操作后，将对该个体中的非法编码部分进行修正，以得到合法解。假设工件J2选择工艺路线4进行加工，J2共有3道工序，各工序的加工方法依次为4→5→6，随机产生两互换位置，分别为1、4，则Swap互换操作及修正操作的示例如图3所示。

图3　Swap互换操作及修正操作示例

2.6Pareto解集构建

多目标优化问题很少存在绝对的最优解[14]，对于多目标优化算法，其求解结果往往是一个Pareto解集。假设种群规模为M，迭代次数为D，初代种群为P，通过以下步骤对Pareto解集进行构建。

(1)初始化Pareto解集，命名为PA，且PA为空集，迭代次数计数器e←0；

(2)对初代种群P的个体进行分层操作，并计算每个个体的拥挤度；

(3)对种群P进行选择、交叉及变异操作，形成下一代种群P′；

(4)建立临时种群Q，Q=P∪P′；

(5)对种群Q中的个体进行分层操作，并计算每个个体的拥挤度；

(6)将种群Q中前沿层级为1的个体与集合PA中的个体比较，将不重复的个体添加到PA；

(7)e←e+1，若e≤D，跳转至步骤(8)；否则，跳转至步骤(9)；

(8)选出种群Q中排名前M的个体，构成新的父代P，跳转至步骤(3)；

(9)对集合PA进行分层操作，删除前沿层级大于1的个体，形成最终Pareto解集。

2.7算法参数说明及算法流程图

M为种群规模，控制种群中个体的数量；CN为竞赛个体总数，为定值，CN

结合上述对算法的描述，可获得非支配排序遗传算法的流程图，如图4所示。

图4　求解MOIPPS问题的NSGA-Ⅱ算法流程

3　实例分析

3.1实例说明

某企业有一笔订单，共有8种不同工件(J1，J2，…，J8)需要加工，有8台加工设备(M1，M2，…，M8)，8种加工方法(P1,P2,…,P8)，16条工艺路线(R1,R2,…,R16)。以makespan最小、加工成本最低及设备最大负载最小为优化目标，使用上述算法对该问题进行求解。各工件对应的工艺路线及加工参数分别如表2～表9所示，各设备的加工成本如表10所示。

表2　工件J1对应的工艺路线及加工参数

表3　工件J2对应的工艺路线及加工参数

表4　工件J3对应的工艺路线及加工参数

表5　工件J4对应的工艺路线及加工参数

表6　工件J5对应的工艺路线及加工参数

表7　工件J6对应的工艺路线及加工参数

表8　工件J7对应的工艺路线及加工参数

表9　工件J8对应的工艺路线及加工参数

表10　各设备的加工成本

3.2假设条件

作如下假设：①所有加工设备从零时刻起均为空闲状态；②工件严格按照工艺顺序加工；③允许工件在工序之间等待，允许机器在工件未到达时闲置；④设备不出现故障。

3.3求解结果与分析

取D=1000、M=100、CN=2、Pc=0.8、Pm=0.1、Pm1=0.5、Pm2=0.5。使用C#语言实现算法编写，在CPU 1.81 GHz、RAM 2 GB的PC主机上运行。算法耗时293 s，Pareto解集中解的个数为62，各解的分布情况如图5所示。

图5　Pareto解集中各解的分布情况

对Pareto解集中的解对应的各目标值进行统计，如表11所示。

表11　Pareto解集中的解对应各目标值的统计结果

分别以makespan、加工成本及设备最大负载为单优化目标，各迭代计算50次，获得50次迭代计算中对应优化目标值最优的解，各最优解对应的目标值如表12所示。

表12　单目标优化所得最优解对应的目标值汇总

以下分别从仅优化makespan、仅优化加工成本及仅优化设备最大负载三个方面，对表11及表12的求解结果进行分析。

(1)仅以makespan为优化目标。当仅以makespan为优化目标时，对应makespan为17.1 h，优于Pareto解集中对应的最低makespan。但由于仅以makespan为优化目标，导致了高额的加工成本，为3598.0元，高于Pareto解集中对应的最高加工成本。

(2)仅以加工成本为优化目标。若仅以加工成本为优化目标，迭代计算时会优先选取加工成本较低的工序，提高了这些工序对应设备的使用频率；而一些加工成本较高的设备，其使用频率则相应较低，导致资源利用不均。仅以加工成本为优化目标，所获得的最优解对应的Gantt图如图6所示。由图6可知，整个制造过程中，相对于其他设备，设备M4、M6及M8的使用频率较高。由于仅以加工成本作为优化目标，对应的makespan及设备最大负载均不低于Pareto解集中对应的最高makespan及最高设备最大负载。

图6　仅优化加工成本所得最优解对应的Gantt图

(3)仅以设备最大负载为优化目标。若仅以设备最大负载为优化目标，一定程度上可以克服仅以加工成本为优化目标导致的资源利用不均问题。但是，由于没有考虑到加工成本，最优解对应的加工成本高于Pareto解集中对应的最高加工成本。

4　结论

(1) 针对MOIPPS问题，同时以makespan、加工成本及设备最大负载为优化目标，建立了该问题的数学模型。

(2) 针对该问题，设计了一种非支配排序遗传算法。以6层编码结构表示可行解；通过分层操作及拥挤度计算，结合偏序关系，使用锦标赛选择法对种群进行选择操作；设计了适用于MOIPPS问题的交叉算子及变异算子。最后，给出了该遗传算法的流程图。

(3) 以实例验证了所建模型的正确性及算法的有效性。一方面，实际生产中，多种目标需要权衡，若仅以单目标作为优化对象，往往导致企业在其他目标上的巨大损失；另一方面，由于设备功能的相似性以及加工手段和技术的多样性，为充分利用各种加工资源，同一道工序可以由多台设备完成，同一工件可能制定多条工艺路线。因此，对MOIPPS问题进行研究，更加符合实际生产环境，通过求解获得的Pareto解集，对于实际调度方案的确定，具有更好的参考与指导作用。

[1]吕盛坪，乔立红．工艺规划与车间调度及两者集成的研究现状和发展趋势[J]．计算机集成制造系统，2014，20(2)：290-300．

Lü Shengping，Qiao Lihong．Current Status and Developing Trend of Process Planning and Job Shop Scheduling[J]．Computer Integrated Manufacturing Systems，2014，20(2)：290-300．

[2]高亮，李新宇．工艺规划与车间调度集成研究现状及进展[J]．中国机械工程，2011，22(8)：1001-1007．

Gao Liang，Li Xinyu．Current Researches on Integrated Process Planning and Scheduling[J]．China Mechanical Engineering，2011，22(8)：1001-1007．

[3]Li Xinyu，Zhang Chaoyong，Gao Liang，et al．An Agent-based Approach for Integrated Process Planning and Scheduling[J]．Expert Systems with Applications，2010，37：1256-1264．

[4]吕盛坪，乔立红．工艺规划与调度复合式集成模型[J]．计算机集成制造系统，2014，20(1)：110-120．

Lü Shengping，Qiao Lihong．Hybrid Integration Model for Process Planning and Scheduling[J]．Computer Integrated Manufacturing Systems，2014，20(1)：110-120．

[5]Phanden R K，Jain A，Verma R．An Approach for Integration of Process Planning and Scheduling[J]．International Journal of Computer Integrated Manufacturing，2013，26(4)：284-302．

[6]Li Xinyu，Zhang Chaoyong，Gao Liang，et al．An Effective Hybrid Algorithm for Integrated Process Planning and Scheduling[J]．Int．J．Production Economics，2010，126：289-298．[7]Li Xinyu，Gao Liang，Shao Xinyu．Mathematical Modeling and Evolutionary Algorithm-based Approach for Integrated Process Planning and Scheduling[J]．Computers & Operations Research，2010，37：656-667．[8]Li Xinyu，Gao Liang，Shao Xinyu．An Active Learning Genetic Algorithm for Integrated Process Planning and Scheduling[J]．Expert Systems with Applications，2012，39：6683-6691．

[9]Wang Jinfei，Fan Xiaoliang，Zhang Chaowei，et al．A Graph-based Ant Colony Optimization Approach for Integrated Process Planning and Scheduling[J]．Chinese Journal of Chemical Engineering，2014，22(7)：748-753．

[10]Seker A，Erol S，Botsali R．A Neuro-fuzzy Model for a New Hybrid Integrated Process Planning and Scheduling System[J]．Expert Systems with Applications，2013，40：5341-5351．

[11]彭建刚，刘明周，张铭鑫，等．基于改进非支配排序的云模型进化多目标柔性作业车间调度[J]．机械工程学报，2014，50(12)：198-204．

Peng Jiangang，Liu Mingzhou，Zhang Mingxin，et al．Cloud Model Evolutionary Multi-objective Flexible Job-shop Scheduling Based on Improved Non-dominated Sorting[J]．Journal of Mechanical Engineering，2014，50(12)：198-204．

[12]张铁男，韩兵，于渤．生产能力约束条件下的柔性作业车间调度优化[J]．系统工程理论与实践，2011，31(3)：505-510．

Zhang Tienan，Han Bing，Yu Bo．Flexible Job-shop Scheduling Optimization Based on Improved Genetic Algorithm[J]．Systems Engineering-Theory & Practice，2011，31(3)：505-510．

[13]刘爱军，杨育，邢青松，等．多目标模糊柔性车间调度中的多种群遗传算法[J]．计算机集成制造系统，2011，17(9)：1954-1961．

Liu Aijun，Yang Yu，Xing Qingsong，et al．Multi-population Genetic Algorithm in Multiobjective Fuzzy and Flexible Job Shop Scheduling[J]．Computer Integrated Manufacturing Systems，2011，17(9)：1954-1961．

[14]施进发，焦合军，陈涛．交货期惩罚下柔性车间调度多目标Pareto优化研究[J]．机械工程学报，2012，48(12)：184-191．

Shi Jinfa，Jiao Hejun，Chen Tao．Multi-objective Pareto Optimization on Flexible Job-shop Scheduling Problem about Due Punishment[J]．Journal of Mechanical Engineering，2012，48(12)：184-191．

[15]陈成，邢立宁．求解柔性作业车间调度问题的遗传—蚁群算法[J]．计算机集成制造系统，2011，17(3)：615-621．

Chen Cheng，Xing Lining．GA-ACO for Solving Flexible Job Shop Scheduling Problem[J]．Computer Integrated Manufacturing Systems，2011，17(3)：615-621．

[16]王云，冯毅雄，谭建荣，等．基于多目标粒子群算法的柔性作业车间调度优化方法[J]．农业机械学报，2011，42(2)：190-195．Wang Yun，Feng Yixiong，Tan Jianrong，et al．Optimization Method of Flexible Job-shop Scheduling Based on Multiobjective Particle Swarm Optimization Algorithm[J]．Transactions of the Chinese Society for Agricultural Machinery，2011，42(2)：190-195．[17]Moslehi G，Mehnam M．A Pareto Approach to Multi-objective Flexible Job-shop Scheduling Problem Using Particle Swarm Optimization and Local Search[J]．Int．J．Production Economics，2011，129：14-22．[18]Shahsavari-Pour N，Ghasemishabankareh B．A Novel Hybrid Meta-heuristic Algorithm for Solving Multi Objective Flexible Job Shop Scheduling[J]．Journal of Manufacturing Systems，2013，32：771-780．[19]王伟玲，李俊芳，王晶．求解多目标作业车间调度问题的双种群遗传算法[J]．计算机集成制造系统，2011，17(4)：808-815．

Wang Weiling，Li Junfang，Wang Jing．Double-population Genetic Algorithm for Multi-objective Job Shop Scheduling Problem[J]．Computer Integrated Manufacturing Systems，2011，17(4)：808-815．

[20]Amin-Tahmasbi H，Tavakkoli-Moghaddam R．Solving a Bi-objective Flowshop Scheduling Problem by a Multi-objective Immune System and Comparing with SPEA2+ and SPGA[J]．Advances in Engineering Software，2011，42：772-779．

[21]Bandyopadhyay S，Bhattacharya R．Solving Multi-objective Parallel Machine Scheduling Problem by a Modified NSGA-Ⅱ[J]．Applied Mathematical Modelling，2013，37：6718-6729．[22]Panahi H，Tavakkoli-Moghaddam R．Solving a Multi-objective Open Shop Scheduling Problem by a Novel Hybrid Ant Colony Optimization[J]．Expert Systems with Applications，2011，38：2817-2822．

[23]曾强，杨育，王勇智，等．复合工艺流程下批量生产车间调度多目标优化[J]．中国机械工程，2011，22(2)：190-196．

Zeng Qiang，Yang Yu，Wang Yongzhi，et al．Multi-objective Optimization Scheduling for Job Shop of Batch Production with Multiple Process Flows[J]．China Mechanical Engineering，2011，22(2)：190-196．

[24]Deb K，Pratap A，Agrawal S，et al．A Fast and Elitist Multiobjective Genetic Algorithm：NSGA-Ⅱ [J]．IEEE Transactions on Evolutionary Computation，2002，6(2)：182-197．

(编辑王旻玥)

Research on Integrated Process Planning and Scheduling Problem with Consideration of Multi-objectives

Li YanBa LiCao YuanLiu YongYang Mingshun

Xi’an University of Technology,Xi’an,710048

Aiming at the shortage of IPPS problem in multi-objective optimization, multi-objective optimization was integrated into IPPS problem. The makespan, processing cost and maximum machine workload were the main targets which will be optimized. The model was built for multi-objective integrated process planning and scheduling problem. A non-dominated sorting genetic algorithm (NSGA-Ⅱ) was proposed for the problem. A multi-layer structure was used to represent solutions. Selection and genetic operators are designed in the algorithm. Finally, the model and algorithm were proved through an application case.

integrated process planning and scheduling; multi-objectives; non-dominated sorting genetic algorithm; selection

2015-02-09

国家自然科学基金资助项目(61402361)；陕西省教育厅科学研究计划资助项目(14JK1521)；陕西省科学技术研究发展计划资助项目(2012KJXX-34)；西安理工大学青年科技创新团队建设计划资助项目(102-211408)

TH166；TH186DOI：10.3969/j.issn.1004-132X.2015.17.012

李言，男，1960年生。西安理工大学机械与精密仪器工程学院教授、博士研究生导师。主要研究方向为先进制造技术、精密加工技术及机电测控技术等。发表论文300余篇。巴黎(通信作者)，男，1986年生。西安理工大学机械与精密仪器工程学院博士研究生。曹源，男，1991年生。西安理工大学机械与精密仪器工程学院硕士研究生。刘永，男，1981年生。西安理工大学机械与精密仪器工程学院副教授。杨明顺，男，1974年生。西安理工大学机械与精密仪器工程学院副教授。