复杂形态孔洞的网格模型修复
2015-10-29袁天然程筱胜孙全平
袁天然 程筱胜 孙全平
1.淮阴工学院江苏省先进制造技术重点实验室,淮安,2230032.南京航空航天大学,南京,210016
复杂形态孔洞的网格模型修复
袁天然1程筱胜2孙全平1
1.淮阴工学院江苏省先进制造技术重点实验室,淮安,2230032.南京航空航天大学,南京,210016
为了满足实际工程应用对复杂形态孔洞修复的需要,模拟拉链闭合原理,并基于局部最优化的权值规则和曲面最小能量值特性的k阶离散欧拉-拉格朗日方程,提出了一种具有C0~C2连续的网格模型修复架构。实验结果表明,该孔洞修复架构能有效地对复杂孔洞边界进行C0~C2连续修复。
三角网格;孔洞修复;复杂孔洞剖分;孔洞修补
0 引言
随着三维测量技术的发展,三角网格模型逐渐成为最常用的几何模型表示形式,广泛应用于计算机图形学、几何建模等领域。由于被测实体表面复杂、局部形态缺失、测量设备受限制等原因,有时无法直接测量获取模型表面的全部三维数据,从而导致生成的网格模型出现孔洞。带有孔洞的网格模型在很多应用领域会导致不良后果,需要对模型孔洞按满足原始模型自然连续属性的方法进行修复[1]。很多学者针对三角网格模型的孔洞修复进行了研究,主要分为非几何方法[2-5]和几何方法[6-11]:①非几何方法主要根据模型孔洞边界顶点及N环邻域顶点的几何属性,构造描述孔洞对应缺失区域的场函数[2]或隐式曲面[3],并采用等值面抽取的方法进行网格化[4],生成对应的修复曲面片。非几何方法生成的修复曲面片具有唯一性,不能根据实际需要实现给定连续性的模型修复,且算法的总体效率较低。②几何方法中比较具有代表性的是采用基于映射平面[9]或者空间的网格化方法[7]对孔洞边界进行三角化剖分,然后对三角化剖分网格进行细分、优化[10]及Reshape调整得到均匀连续的修复曲面片[8,12]。该类算法的关键是对孔洞边界的三角化剖分和后续的Reshape处理。基于映射平面的剖分方法在处理形状简单的孔洞边界时,具有较好的效果,但在处理曲率变化剧烈、形态复杂的孔洞时,投影后产生的自相交使剖分结果出现剧烈“凹陷”。常用的空间三角化剖分方法[7]为NP complete问题,具有O(N3)的复杂度,不适合处理顶点较多的模型边界。同时,现有的对修复曲面片Reshape调整的方法通常基于径向基函数[6]、最小化能量函数[13]和光顺算法[8,11]等,难以取得指定连续性的修复结果,对复杂形态孔洞修复的效果较差。
针对现有孔洞修复方法效率低、修复结果单一、不能有效处理复杂形态孔洞的问题,本文深入研究分析了在对孔洞边界进行空间三角化剖分时的各种影响因素后,基于局部最优化的权值规则和曲面最小能量值特性的k阶离散欧拉-拉格朗日方程,提出了一种能有效地对复杂孔洞边界进行Ck-1(k=1,2,3)连续的三角网格模型修复算法。本文所提出的修复算法主要由封闭孔洞边界的三角化剖分、剖分网格的细分优化以及后续的Ck-1连续变形调整三个步骤组成。
1 孔洞修复算法及其实现
1.1符号定义
对网格模型中的任意顶点vi,用NV,1(i)表示顶点vi的一环邻域顶点集合,NT,1(i)表示顶点vi的一环邻域三角形集合。|NV,1(i)|表示集合中顶点的个数,|NT,1(i)|表示集合中三角形的个数。NT,1(i)中的三角形在顶点vi处对应的内角称为vi的邻接内角(图1中的Aj、Ak),定义A(vi)为NT,1(i)在vi处的邻接内角之和:
(1)
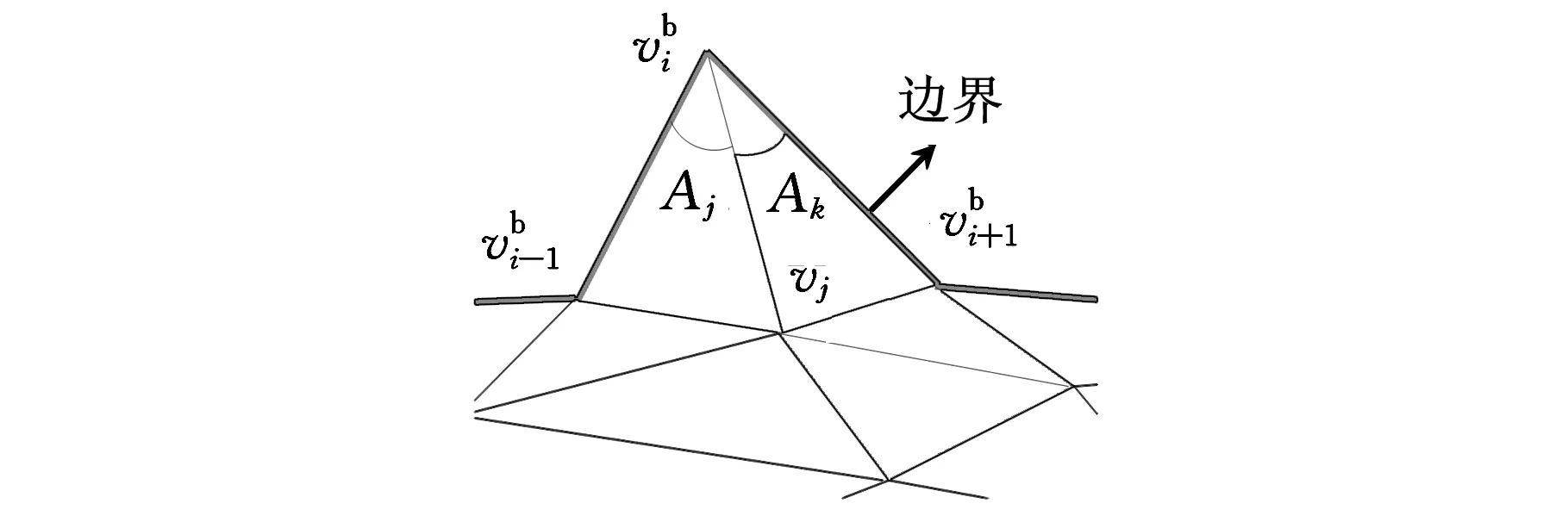
图1 尖锐棱角对应的初始边界
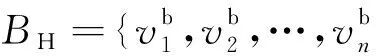
对网格模型进行孔洞修复时,相应符号定义如下:孔洞边界三角化剖分生成的网格用MC表示;MC细分、优化后生成的网格用MRO表示;MRO进行Reshape调整后生成的最终修复网格用MF表示。
1.2孔洞边界的三角化剖分
(1)新增三角形后,待删除顶点及其一环邻域顶点组成的多面体,应与周边网格近似连续过渡,避免形成尖锐的棱角,使新增的网格表面出现凸凹不平和褶皱。
(2)剖分过程中,应避免同一边界顶点包含过多的邻接三角形,使剖分结果产生扭曲。
(3)生成的剖分网格中的边,应均匀地分布在孔洞边界上。
1.2.1顶点一环邻域内角因素
当顶点vi为网格模型内部任意顶点时,A(vi)的大小表示网格模型在该点处的“平坦”度,A(vi)越大,当前顶点与其一环邻域顶点共面度越大,网格模型内部的连续性越好;A(vi)较小的顶点,在模型表面会形成粗糙的特征,不仅影响后续的模型处理,而且对视觉效果有着不良影响。A(vi)≈2π时,顶点vi的邻接内角∃j∈NT,1(i);Aj≈π时,曲面的连续性发生剧烈变化。因此应避免生成A(vi)较小及存在邻接内角接近于π的新增三角形。

(a)生成尖锐棱角(b)生成内角近于π的三角形图2 新增三角形后生成的非“平坦”情况
1.2.2顶点一环邻域三角形因素

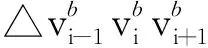
1.2.3三角形边长因素

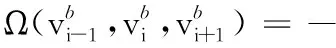
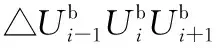
1.2.4权值及三角化剖分算法
经对孔洞边界三角化剖分时可能产生影响的因素进行综合分析以及实际的编程验证后,权值Ω及lless、lbigger相应的计算公式如下:
(2)
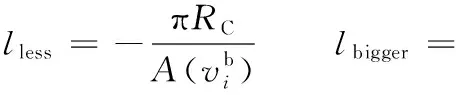
式中,RC为模型的包围球半径。
三角化剖分算法描述如下:
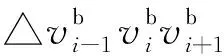
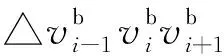
1.3三角化剖分网格的细分及优化
由于三角化剖分网格MC中的边由BH中的顶点直接连接而成,故需对MC进行细分、优化,得到与原始网格模型网格密度相近的曲面片。网格模型的密度通常是由三角形的平均边长度量的,因此本文采用1-3“面分裂”方法,将边长较大的三角形△vivjvk按图3a所示的方式进行分裂,新增顶点为三角形的质心坐标vc,并采用边交换的方法进行优化调整,得到边长均匀且近似符合Delaunay划分准则的曲面片MRO[10](见图3b、图3c)。
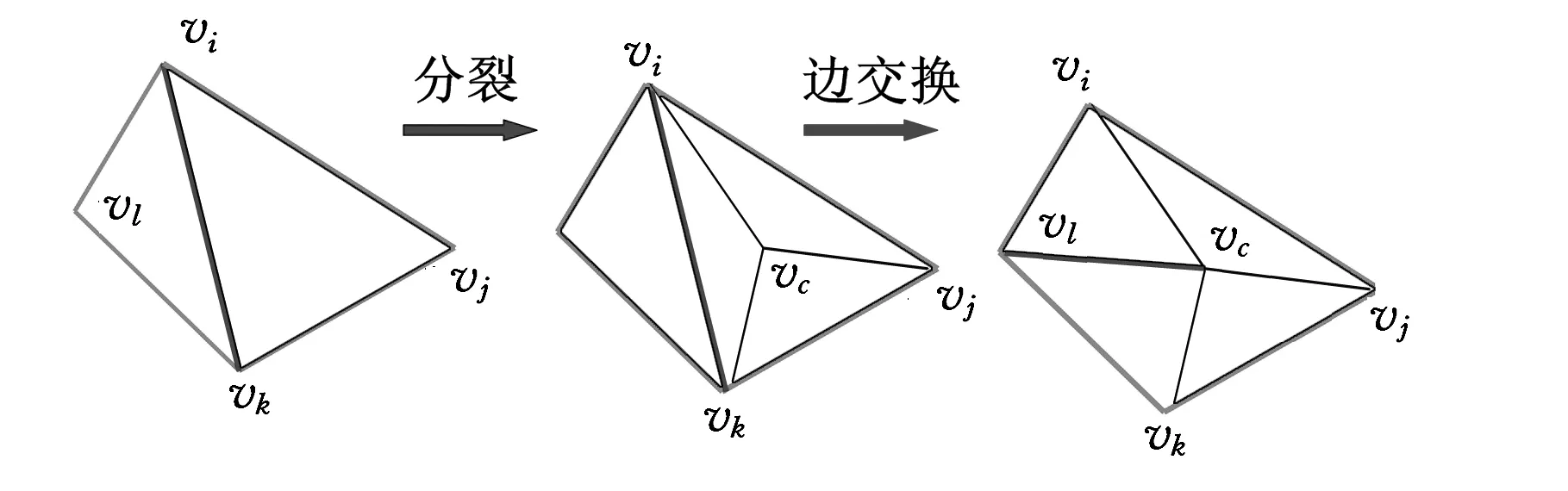
(a)三角形的细分、优化机制
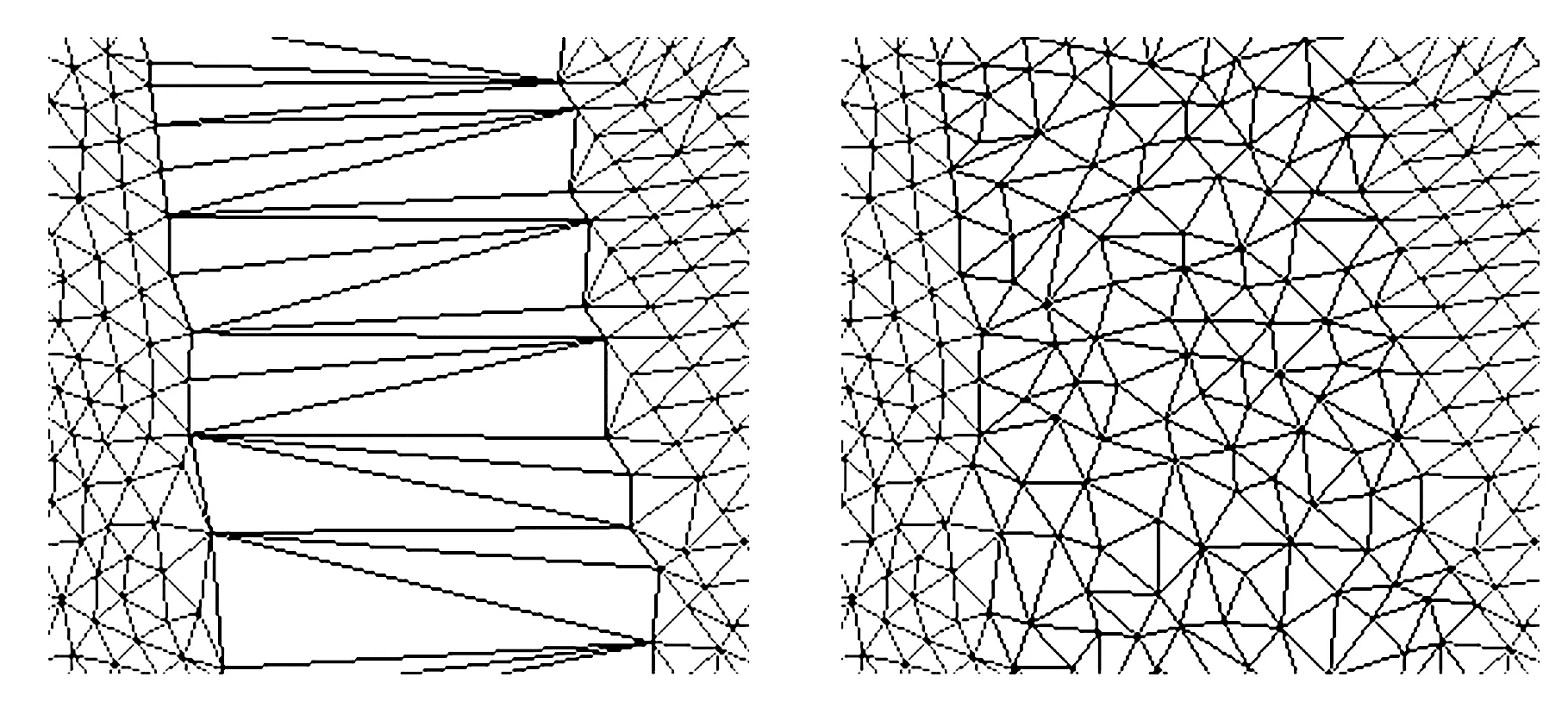
(b)三角化剖分网格(c)细分、优化实例图3 三角化剖分网格的细分、优化
1.4Ck-1连续的形状恢复
MC经过细分、优化后得到的网格MRO仍为边界和内部均为C0连续的曲面片。为得到在边界和内部符合Ck-1连续性约束的曲面片,图形学领域中,在给定边界信息和边界约束条件的情况下,通常采用最小能量定律来实现曲面片的Ck-1连续Reshape调整[12-13]。因用二次函数表示的能量函数在求解时有着较高的效率和较好的稳定性,故本文基于二次能量函数的通用表示方式,设计了一种能实现Ck-1连续的Reshape调整框架,框架的设计过程如下:
设S:Ψ→R3为三角网格模型M对应的连续曲面,S*…*表示曲面的k阶偏导数,δΨ为曲面的边界。其对应的二次能量函数为
Ek(S)=∫SFk(Su…u,Su…uv,…,Sv…v)
(3)
通常应用变分的方法对等式(3)进行求解,以得出对应最小能量值特性的欧拉-拉格朗日方程:
(4)
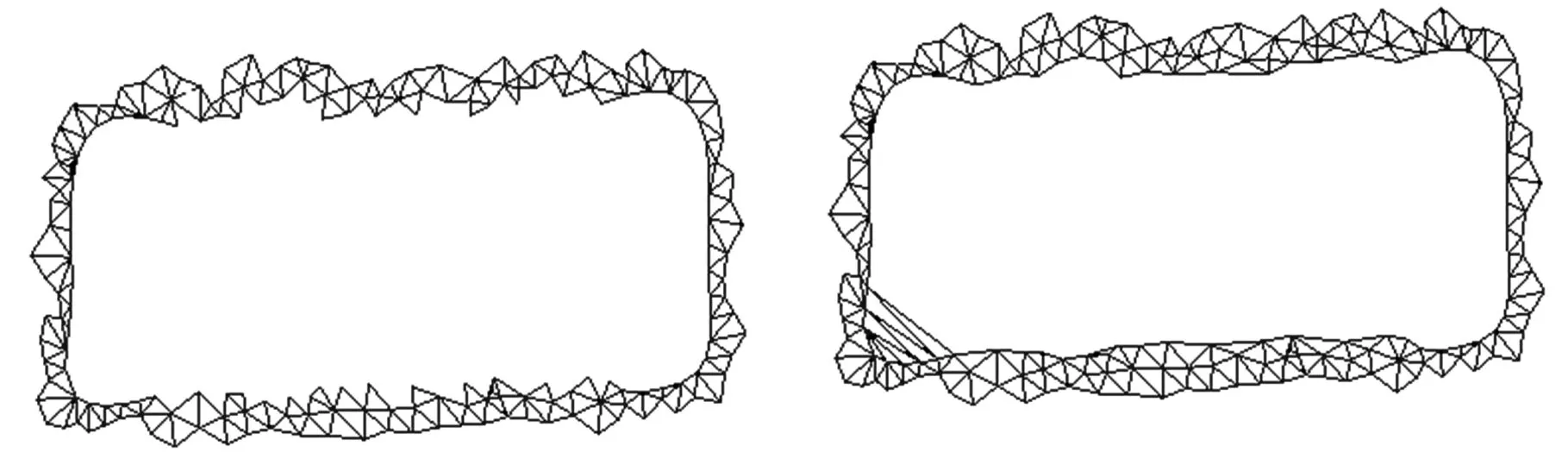
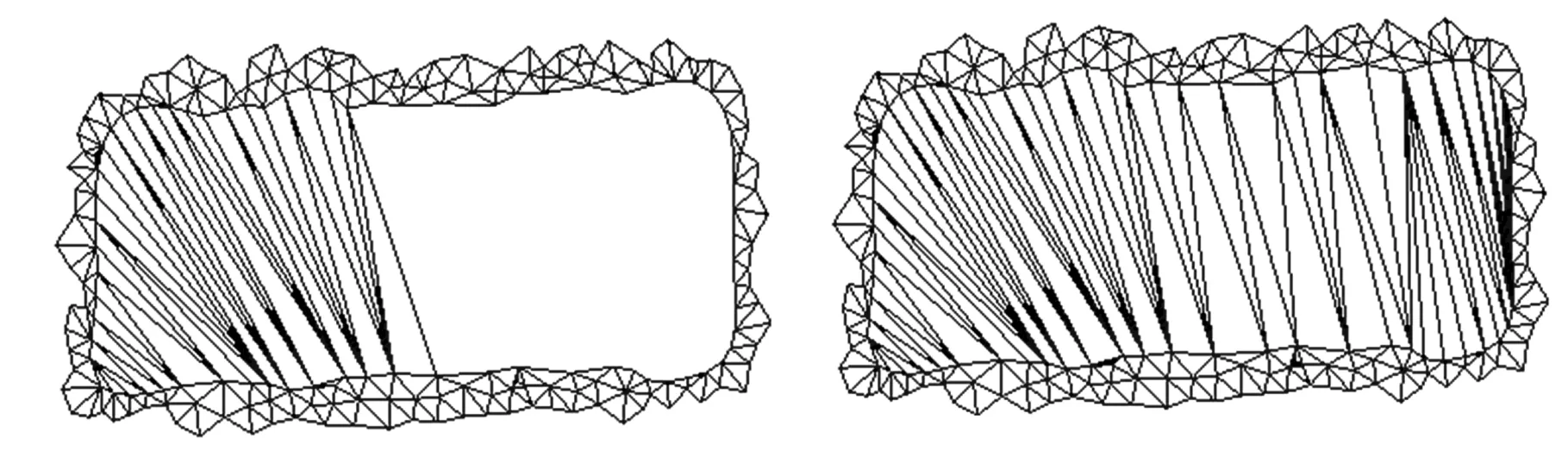
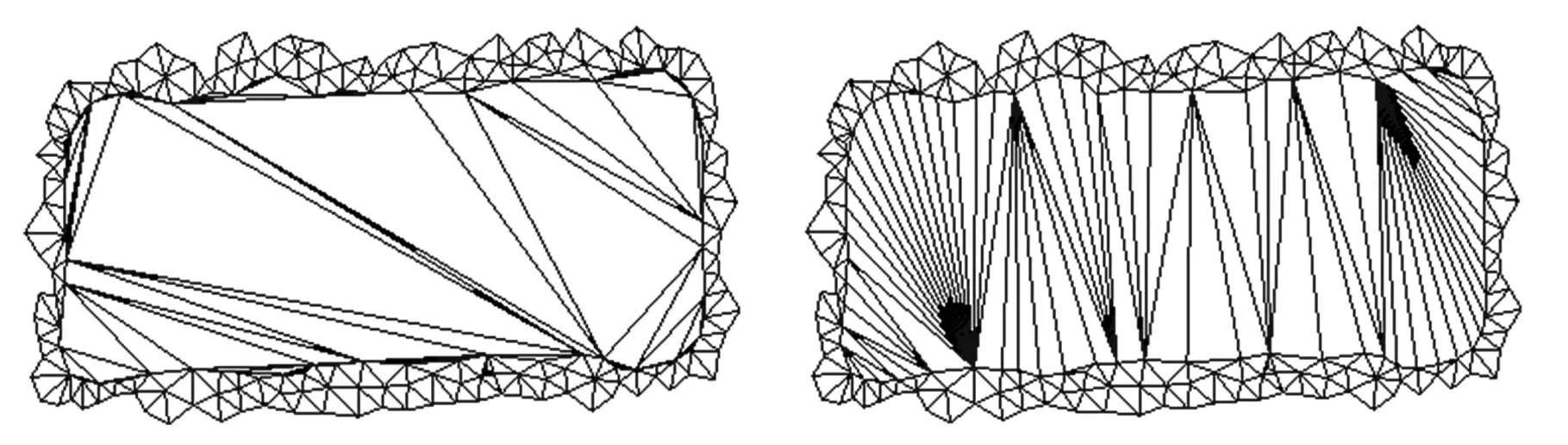
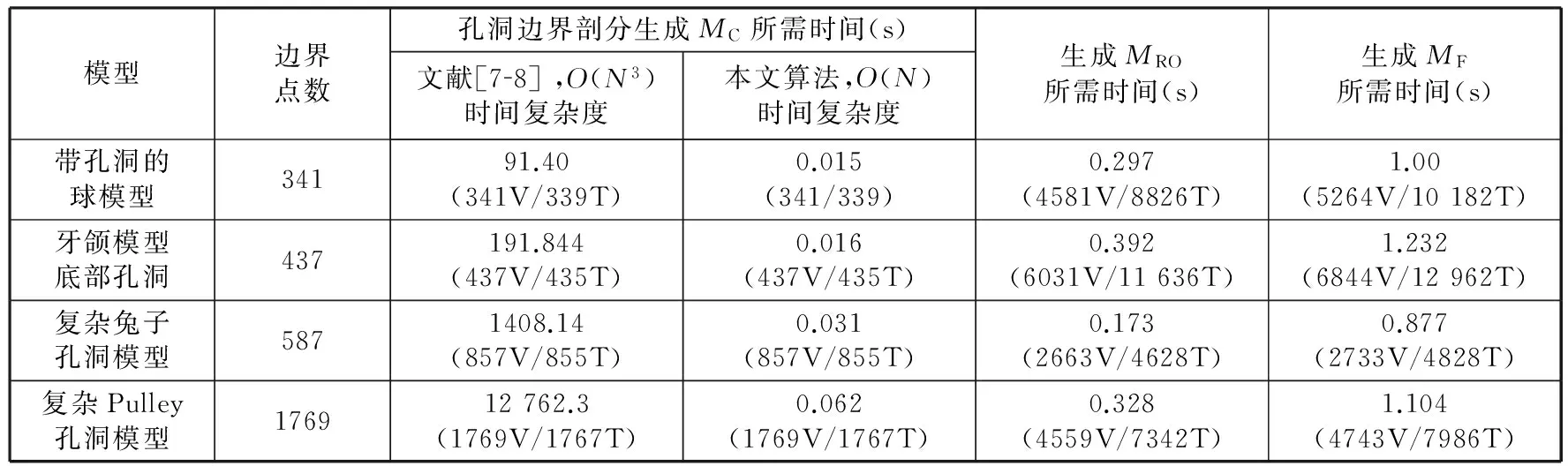
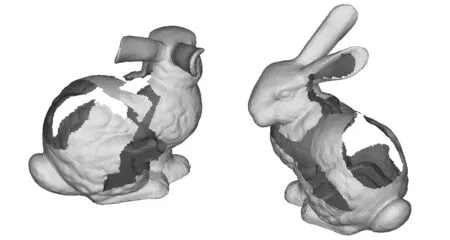
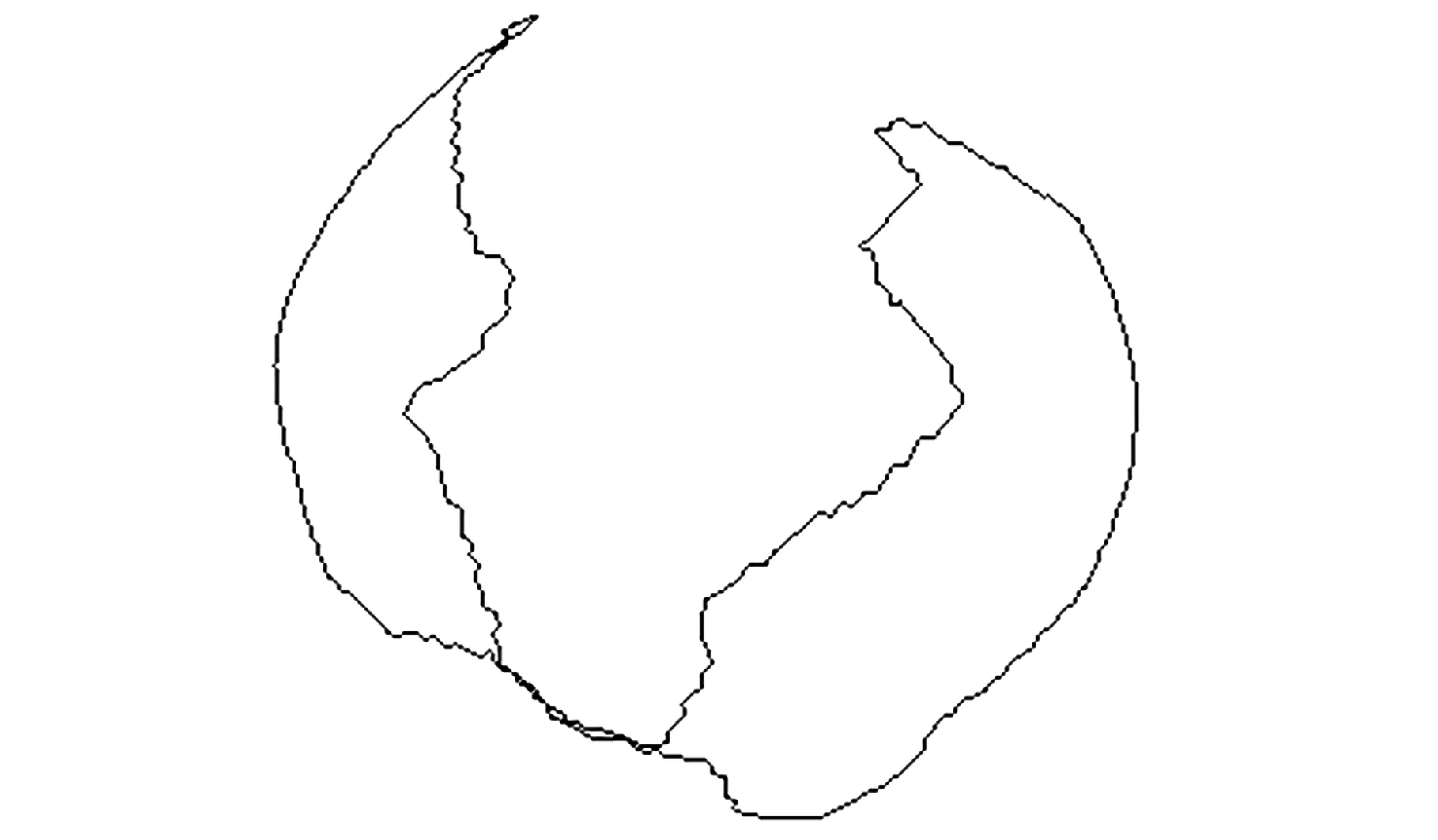
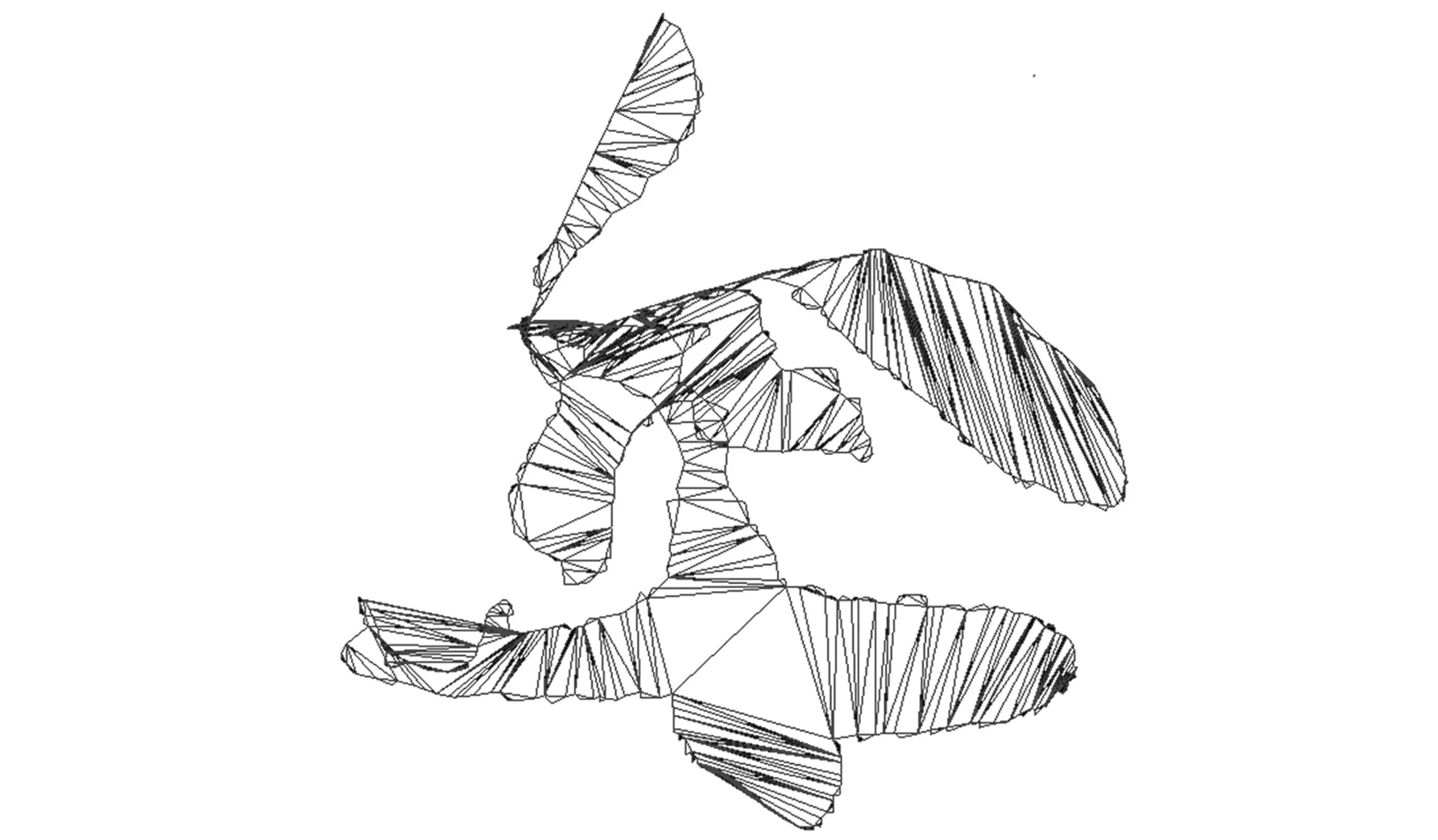
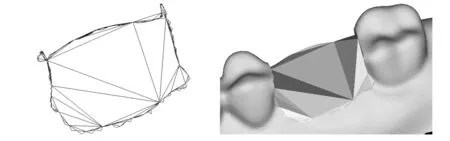
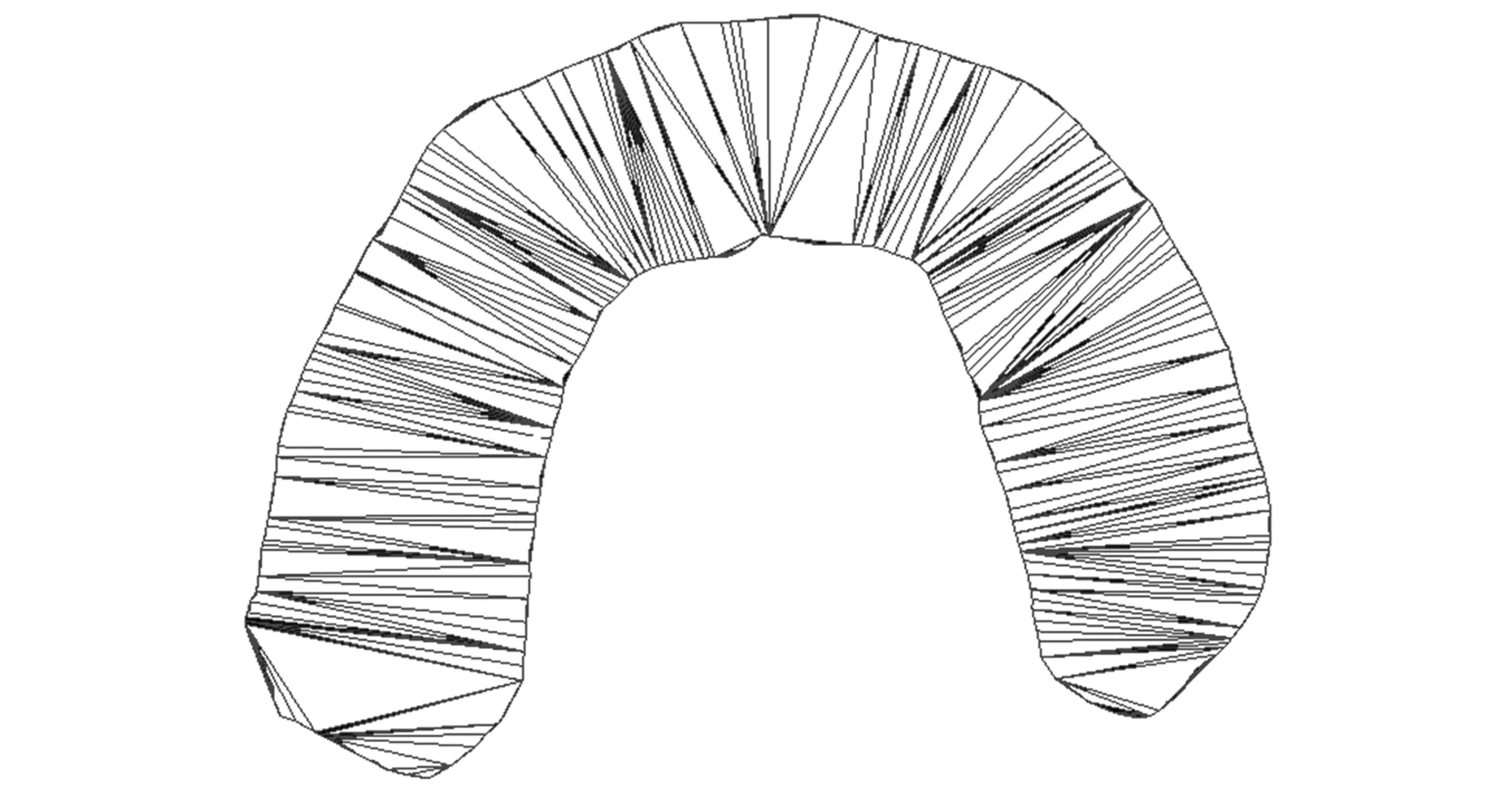
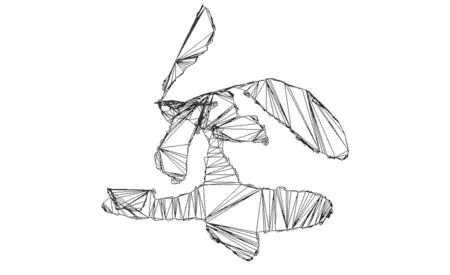
其中,Δ为拉普拉斯算子;bj为具有j(j 当用三角网格曲面取代连续曲面时,式(4)中的拉普拉斯算子对应离散为 (5) 其中,S(vi)为顶点一环邻域三角形的面积之和;αi j、βi j为边ei j的对角。k阶的拉普拉斯算子通过迭代定义求出: (6) 对拉普拉斯算子进行离散后,式(4)转化为带有稀疏矩阵的线性方程: (7) 其中,P=[vp,1vp,2…vp,n]T表示网格模型M的内部的自由顶点;B=[vb,1vb,2…vb,m]T表示具有Ck-1边界连续的约束顶点,对应为边界顶点的k-1环邻域顶点集合(包含边界顶点);n、m为对应顶点个数。根据设计的变形框架,对优化细分网格MRO中的顶点,按照给定的边界连续性约束进行调整后得到MF。 2.1剖分算法工作机理分析 图4e所示为不考虑邻接内角约束时,对图4a中孔洞剖分的结果,图4f所示为不考虑邻接三角形个数约束时,对图4a中孔洞剖分的结果。由剖分结果可知,邻接内角约束主要影响剖分生成的三角片大小,邻接三角形个数约束主要影响剖分结果在孔洞边界上的均布性。 (a)初始孔洞(b)消除“锯齿”生成拉合起点 (c)由权值规则驱动闭合孔洞(d)最终剖分结果 (e)无邻接内角约束剖分结果(f)无邻接三角形个数约束剖分结果图4 孔洞剖分机理分析 孔洞剖分过程中,剖分算法会在多个分支的“交汇处”生成较大的三角形,对多个分支进行闭合。 本文所提的权值规则使剖分过程近似分为边界平滑和边界“拉合”的过程,使得剖分结果能张紧在孔洞边界,得到均匀、自然和无扭曲的剖分。 2.2算法效率分析 由于对孔洞边界采用局部最优化的权值规则,基于迭代删除顶点的方法进行三角化剖分,三角化剖分阶段对应的时间复杂度为线性O(N)(N为边界顶点个数)。对三角化剖分网格MC的细分、优化,以得到与原始网格模型密度相近的网格MRO,其对应的时间复杂度为线性O(M)(M为优化细分后得到的三角形的个数)。在对矩阵的求解阶段, 本文采用增量最小二乘求解矩阵的方 法,基于CPU(P4 2.4 GHz)的速率可达每秒5万个顶点。因此,本文所提的模型修复算法,具有较高的效率,且算法的鲁棒性较好。 表1显示了本文算法在对网格模型修复过程中,生成MC、MRO和MF各步骤所用时间,并与文献[7-8]的剖分算法进行了对比。表1数据表明,利用本文的剖分算法对模型进行修复时,剖分效率为每毫秒200~300个顶点,修复效率为每秒3000~5000个顶点, 适合应用于修复地形、 文物 表1 对模型修复过程中各步骤所需时间,新生成的顶点(V)/三角形(T)的个数 等包含海量级数据的大尺寸三维模型。 2.3应用举例 本节对带有大面积缺失的球模型(图5a)、牙颌模型(图5b、图5c)、 兔子模型(图5d、图5e)、 (a)球孔洞模型 (b)牙颌孔洞模型1(c)牙颌孔洞模型2 (d)兔子单个复杂孔洞模型1(e)兔子单个复杂孔洞模型2 (f)Pulley单个复杂孔洞模型1(g)Pulley单个复杂孔洞模型2图5 孔洞模型 Pulley上的孔洞(图5f、图5g),进行了实验分析。 图6a显示,采用映射平面剖分时,由于孔洞边界曲率变化剧烈,模型缺失面积较大,投影后的边界会产生自交。图6b为基于映射平面法所生成的修复结果,其并不能满足实际需要。 (a)边界在其最小二乘平面上的投影 (b)基于映射平面法的修复结果图6 平面映射平面部分的结果 (a)齿间孔洞 (b)底部孔洞 (c)兔子孔洞 图7 本文算法所得剖分结果 图7a、图7b、图7c显示,在利用本文算法对孔洞边界进行三角化剖分时,能得到均布在孔洞 边界上的剖分结果。 图8a、图8b、图8c为采用文献[7-8]面积最小化的剖分结果,剖分过程中没有对顶点的邻接三角形个数和邻接内角进行限制,这使得剖分结果会产生扭曲和生成内角接近于π的三角形。 由于对相同的孔洞边界无论采用何种剖分方法,总会得到具有相同三角形个数的剖分结果,因此,对空间孔洞边界的剖分好坏的判断标准,即为剖分后生成的边在孔洞边界上的均布性。由图7a、图7b、图7c可知,本文算法剖分得出的三角形更为均匀合理。 图9显示了利用本文算法,对模型进行具有不同边界连续性和内部连续性的修复结果。图10、图11显示,本文算法可以处理带有大面积缺失的复杂孔洞模型,对孔洞的修复结果均匀自然。由实例分析可知,本文算法能实现对模型不同连续性的修复,修复后的网格密度与原始网格密度相近,能满足实际工程的需要。 (a)齿间孔洞 (b)底部孔洞 (c)兔子孔洞图8 文献[7-8]算法所得剖分结果 (c)边界C1连续(d)边界C2连续图9 球模型的孔洞修复 图11 复杂Pulley孔洞模型边界C1连续修复结果 本文深入分析了对三角网格模型孔洞边界进行剖分时的各种影响因素,根据二维流形网格模型的特性,对剖分过程中由边界顶点组成的候选三角形进行加权,使得对空间孔洞边界的剖分转化为边界平滑和边界“拉合”的过程,得到成“帘幕”状均布在孔洞边界上的三角化剖分网格。对三角化剖分网格进行细分、优化后操作后,采用基于能量最小化定律的方法进行Reshape调整,从而实现具有Ck-1连续的模型修复。由最终的修复模型可知,本文算法能根据模型的部分信息来恢复网格模型,可用于网格模型的压缩。本文算法简单、易于理解,能处理形状复杂、大面积缺失的网格模型孔洞,具有较好的工程应用价值。 [1]Attene M,Campen M,Kobbelt L. Polygon Mesh Repairing:an Application Perspective[J].ACM Computing Surveys,2013,45(2):1-37. [2]Davis J,Marschner S R,Garr M,et al. Filling Holes in Complex Surfaces Using Volumetric Diffusion[C]//First International Symposium on 3D Data Processing Visualization and Transmission.Padua,Italy,2002:428-441. [3]Wu X J,Wang M Y,Han B. An Automatic Hole-filling Algorithm for Polygon Meshes[J]. Computer-aided Design and Applications,2008,5(6):889-899. [4]Zhou K,Gong M,Huang X,et al. Data-parallel Octrees for Surface Reconstruction[J]. IEEE Transactions on Visualization and Computer Graphics,2011,17(5):669-681. [5]Marchandise E,Piret C,Remacle J F.CAD and Mesh Repair with Radial Basis Functions[J].Journal of Computational Physics,2012,231(5):2376-2387. [6]杜佶,张丽艳,王宏涛,等. 基于径向基函数的三角网格曲面孔洞修补算法[J]. 计算机辅助设计与图形学学报,2005,17(9):1976-1982. Du Ji,Zhang Liyan,Wang Hongtao,et al. Hole Repairing in Triangular Meshes Based on Radial Basis Function[J]. Journal of Computer-Aided Design & Computer Graphics,2005,17 (9):1976-1982. [7]Barequet G,Sharir M.Filling Gaps in the Boundary of a Polyhedron [J]. Computer Aided Geometric Design,1995,12(2):207-229. [8]Liepa P. FillingHoles in Meshes[C]//Proceedings of the 2003 Eurographics/ACM SIGGRAPH Symposium on Geometry Processing.Aire-la-Ville,Switzerland,2003:200-205. [9]Li G,Ye X Z,Zhang S Y. An Algorithm for Filling Complex Holes in Reverse Engineering[J]. Engineering with Computers,2008,24(2):119-125. [10]Pfeifle R,Seidel H P.Triangular B-splines for Blending and Filling of Polygonal Holes[C]//Proceedings of the Conference on Graphics Interface. Ontario,Canada,1996:186-193. [11]韦争亮,钟约先,袁朝龙,等. 三角网格大面积孔洞光顺修补算法的研究[J]. 中国机械工程,2008,19(8):949-954. Wei Zhengliang,Zhong Yuexian,Yuan Chaolong. Research on Smooth Filling Algorithm of Large Holes in Triangular Mesh Model[J]. China Mechanical Engineering,2008,19(8):949-954. [12]Botsch M,Kobbelt L. An Intuitive Framework for Real-time Freeform Modeling[J]. ACM Transactions on Graphics (TOG),2004,23(3):630-634. [13]Bobenko A I,Schröder P. Discrete Willmore Flow[C]// Eurographics Symposium on Geometry Processing.Aire-la-Ville,Switzerland,2005:101-110. (编辑张洋) Mesh Model Restoration for Complex Holes Yuan Tianran1Cheng Xiaosheng2Sun Quanping1 1.Key Lab of Advanced Manufacturing Technology of Jiangsu Province,Huaiyin Institute of Technology,Huaian,Jiangsu,223003 2.Nanjing University of Aeronautics and Astronautics,Nanjing,210016 In order to meet the practical engineering application needs of complex hole restoration,this paper proposed a robust mesh model restoration architecture with C0~C2continuity based on zipper closure principle and thekorder discrete Euler-Lagrange equation derived from minimizer of the surface energy functional.The final experimental results show that the proposed hole restoration method can deal with complex holes efficiently and correctly. triangular mesh;hole restoration;complex hole boundary triangulation; hole repairing 2014-05-15 国家自然科学基金资助项目(51075173);江苏省自然科学基金资助项目(BK2010288) TP391.72;R783.4DOI:10.3969/j.issn.1004-132X.2015.12.019 袁天然,男,1982年生。淮阴工学院机械工程学院讲师、博士。主要研究方向为逆向工程、数字口腔医疗装备。发表论文10余篇。程筱胜,男,1964年生。南京航空航天大学机电学院教授、博士研究生导师。孙全平,男,1969年生。淮阴工学院机械工程学院教授。2 实验分析
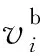







3 结语
