多元非参数rank图在民航发动机监控中的应用
2015-10-29孔祥芬
孔祥芬 张 兵
中国民航大学,天津,300300
多元非参数rank图在民航发动机监控中的应用
孔祥芬张兵
中国民航大学,天津,300300
发动机多元监控可以很好地解决以往单参数监控中监控参数过多导致指示过程失真的问题。分别利用T2控制图和rank图对发动机低压转子振动值和高压转子振动值两个参数同时进行实时监控,并对两种控制图在实时监控中的表现进行了比较分析,结果显示,rank图在多元实时监控中的表现优于T2控制图。
数据深度; rank图; 发动机监控;T2控制图
0 引言
民用航空业的快速增长对航空安全的要求越来越迫切,而作为飞机“心脏”的发动机的监控也变得越发重要。现代计算机技术的高速发展使得我们可以利用ACARS(aircraft communications addressing and reporting system)下传或利用QAR(quick access recorder )存储来获得飞机运行时的发动机监控数据,并对其进行实时监控或者进行事后分析[1]。及时发现发动机监控数据早期的异常情况可以为随后的故障诊断提供依据,从而可及时制定合理的维修方案,防止故障过程的持续恶化并造成一系列的继发损害。对发动机监控数据处理方法的研究经历了单变量到多变量、经典统计学到非参数方法的过程。最早对发动机参数数据进行监控时采用单个参数分别监控的方式[2],人们对单参数监控方法进行了相应的研究。Fisher[3]提出了顺序组合转换方法(RPT),即定义一个检验统计量之后比较当前数据与过去数据的区别;Eklund等[4]给出了RPT的详细算法。Hinkley[5]提出了似然比检验(LRT)的思想,该思想已经被用于检验时间序列样本数据(发动机监控数据就是时间序列样本数据的一类)分布的变化情况[6]。但实际应用中,在同时分别监控多个单参数过程中多个单参数控制限的应用会使得参数的指示过程处于失真状态,且这种失真状态随着监控参数的增加而更加严重[7]。为了解决这一问题,并且为了提高参数的监控效率,更快更准确地发现参数的异常情况,Hu等[8]将多元参数控制的思想引入发动机监控中。这种多元监控的方法将对单变量监控时多个参数分别指示的情况替代为利用一个参数来指示,这可以很好地弥补单变量监控过程中的失真情况[8],但是这种多元监控方法应用的多元T2控制图[9]主要监控多元数据的趋势变化,并未涉及多元数据的实时超限的监控情况。本文的目的就是要推行一种基于数据深度的多元非参数方法来监控多元数据的实时超限情况,并对多元T2控制图的实时监控表现进行验证,比较两者的优劣。
1 基于数据深度的控制图
对于一个给定的多变量样本,数据深度可用来测量它们的深度或外围数据相对于中心数据的分布情况。而数据深度的测量过程使得样本点排列顺序变为中心向外。基于这种中心向外的顺序,Liu[10]介绍了一简单而有效的控制图监测多元观测值,并将其用于监控多元航空安全数据[11]。
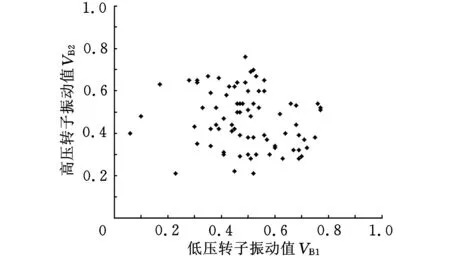
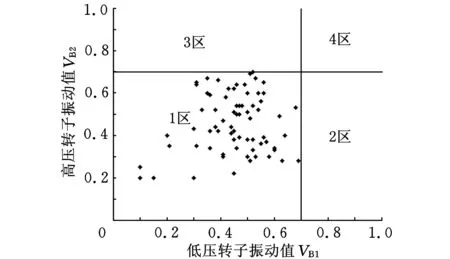
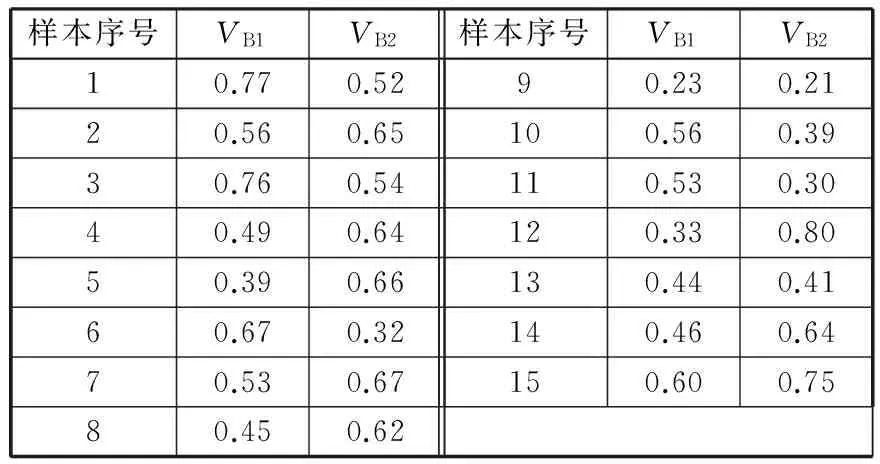
1.1单纯形深度
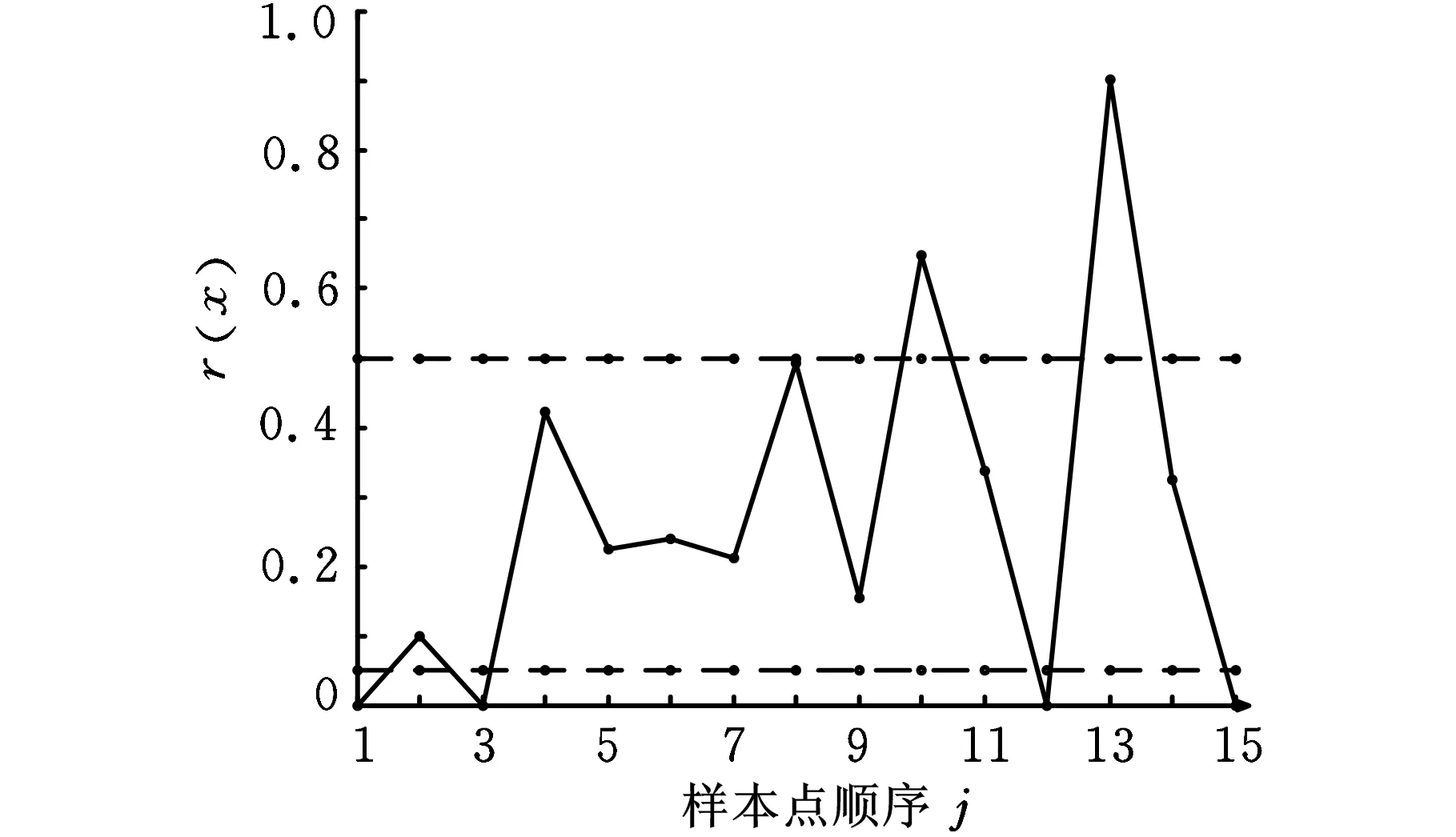
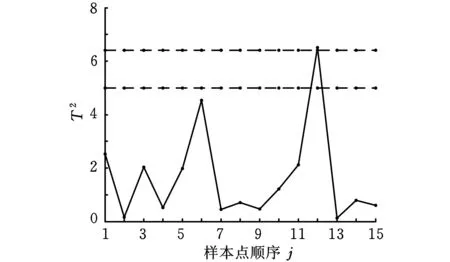
单纯形深度由包含该数据的单纯形个数来决定。令{Y1,Y2,…,Yn}为样品的p维观察值,p (1) 其中,I(A)为符号函数,当A为真时,I(A)=1,当A为其他情况时,I(A)=0。 式(1)的概率表示为 DG(y)=PG{y∈S{Yi1,Yi2,…,Yip+1}} (2) 即包含y点的单纯形个数占总单纯形个数的比例。而检验y点是否包含在以{Y1,Y2,…,Yp+1}为顶点的单纯形中的方法就是检验y是否可以表示为{Y1,Y2,…,Yp+1}的凸组合,即 y=r1Yi1+r2Yi2+…rp+1Yip+1 (3) (4) 解出关于ri的p+1维方程组,检验ri是否满足条件式(4),如果满足则y包含在单纯形中。 容易看出,单纯形深度函数DG(y)的值介于0和1之间,单纯形深度函数值越大表明y在参考集数据{Y1,Y2,…,Yn}中的位置越靠近中心。 计算所有Yi的值,并将其按照大小排序,令最小值为Y[1],最大值为Y[n],排序之后,Liu等[12]提出一个新的统计量r(x),其表达式为 r(x)=#{Yj|D(Yj)≤D(X),j=1,2,…,n}/(n+1) (5) 其中,#{·}表示对满足{·}条件的数据点进行计数。 1.2rank图 文献[10]中,画出r(x)值的控制图被用来监测多元观测值,具体过程如下:计算每个新的观测值xi的r(xi),并按照序列顺序画在控制图上,假设xi遵循一个p维分布函数F,rank图的绘制等价于检验命题假设H0与H1。其中命题假设H0的含义为分布F等于分布G;命题假设H1的含义为存在一个从分布G到分布F的均值漂移和/或方差变异。在命题假设H0下,Liu等[12]证明r(x)在单位区间上收敛于均匀分布,即 r(x)→U[0,1] (6) 其中,U[0,1]表示定义在[0,1]上的均匀分布。因此该rank图的中心线(CL)设置为0.5,控制下限(LCL)设置为α,与H0的α水平检验相对应。实际上α是使用rank图时的错误报警率。 需要注意的是,由于r(x)值越大代表该数据在参考集中的位置越靠近中心,即该数据越“正常”,因此,rank图不使用控制上限,同样可以达到需要的监控效果[11]。 2.1监控参数的选取 本文所用的发动机监控数据由某航空维修基地提供,虽然基于数据深度的rank图可以监控任意维数的数据,但为了简便并可同时测试控制图的监控效果,我们选取2个参数来建立rank图并进行分析。为了更好地显示多元监控的效果,本文选取低压转子振动值VB1和高压转子振动值VB2来进行同时监控,选取这两个参数的目的在于,这两个参数一旦有一个发生变化即表明发动机转子振动值超限,发动机出现了结构故障[13-14],需要维修人员及时进行排查故障。而实时监控的主要目的就是及时发现故障并反馈给驾驶员,并采取相应措施,所以这两个参数具有代表性。 2.2参考集的选取 建立rank图的过程中通常选取给定数据样本中最集中的80%的数据作为参考集[12],并根据所选参数的特点来适当扩充参考集,比如在振动值相对较小的方向上适当扩充以保证振动值较小的点有适当的数据深度,使其与真正的超限点区分开来。本文所用低压转子振动值VB1和高压转子振动值VB2的阈值由维修基地提供,两者均为0.7。并且,为了便于观察,将样本值所在区域划分为如下4个区域: (1)1区为0≤x≤0.7,0≤y≤0.7。 (2)2区为x>0.7,0≤y≤0.7。 (3)3区为0≤x≤0.7,y>0.7。 (4)4区为x>0.7,y>0.7。 则本文中所选样本超限点所在区域为2、3、4区。参考集的选取过程如下: (1)观察样本数据分布情况。本文选取的二维样本数据如图1所示。 图1 样本数据分布图 (2)根据rank图的建立方法,选取最靠近中心约80%的样本数据并适当扩充,作为本文建立rank图过程中的参考集(在振动值较小的方向扩充了适当的点以保证振动值较小的点可以被识别)。所建立的参考集如图2所示。 图2 参考集数据分布图 (3)根据所监控参数的实际情况,建立参考集过程应注意如下问题:①监控参数选取时应该注意两者转化成标准值后的数值所在的范围不能差距太大,如本文中选取两个振动值所在范围均是(0,1),这样可以保证参考集可以从任意方向上有效识别超限点。如果监控参数所在范围差距过大,则会出现在参数变化幅度较小的方向上参考集反应不灵敏的情况。②参考集选取过程中如果在超限的区域上选取了适当的点,那么一般要保证在两个参数各自超限的区域(2、4区)参考集点的分布尽量对称,这样做的目的是保证控制限可以同时判定出来自两个方向上的数据变化,并且不会对设置控制限造成影响。 2.3利用选取的参考集建立新样本rank图 我们选取的新样本如表1所示。 表1 发动机转子振动值 计算每个新样本点在选取好的参考集下的r(x)值,并将值记录在控制图中,即为新样本的rank图。 对15个新样本点建立的rank图见图3。由于本文中设置的控制限均为0.7,因此表1中的新样本数据第1个点(0.77,0.52)、第3个点(0.76,0.54)在x方向(VB1)上超限,而第12个点(0.33,0.8)、第15个点(0.6,0.75)在y方向(VB2)上超限,观察图3中的结果,第1、3、12、15个点处于控制线之外,换言之,表1中的所有超限数据均被检测出来。表1中的第9个点振动值较小,但由于修正了参考集,也在图3中被识别出来(第9个点并未显示超限)。由实际测试可以看出,应用该控制图后,一旦发现超限点,则表明发动机转子振动值中有超限现象,从而表示发动机转子系统出现了结构故障,如工作叶片折断或部分损坏,工作叶片安装不合适(尤其是现代涡扇发动机的风扇叶片),转子上有部件丢失(如螺栓、螺母等)[14],应该及时查明原因,排除故障。 图3 新样本数据rank图 2.4控制限的设置 从图2中可以看出,由于本文选取参考集时在超限区域没有选取参考点,使得超限点的深度变为0,如果在超限区域选择一些点作为参考集的一部分,则超限值的数据深度将不为0,相应的r(x)也不为0,所以,控制限的设置与参考集的选取有直接关系。当参考集选取比较集中时(如本文选取的参考集),将控制限选取为0.05即可有效区别出超限点,当超限区域有适当的点作为参考集的一部分时,可分别计算处在两个参数基线位置的参考集点和样本点的r(x)值,并选取最小值作为控制限。 3.1经典多元控制图 (8) 3.2针对发动机监控数据的多元T2控制图的建立 在rank图的建立过程中,本文选择样本数据80%的中心数据作为参考集,在这里,同样应用这些参考集中的数据来估计总体的均值和协方差矩阵,因为本文选取作为参考集的数据代表了发动机正常的运行状态,所以样本中的超限点已经在参考集的选取过程中提前剔除了。rank图的建立步骤如下:①计算参考集的均值和协方差矩阵;②计算每个样本点的T2值;③计算控制图的控制上限LUC。 本文建立的关于VB1和VB2的多元T2控制图如图4所示。 采取委托管理、连锁运营的方式,通过专业化服务、科学化管理,做好总分馆日常管理运行。建立合格主体单位目录库,采用政府购买服务方式,引入合格的第三方主体参与公共图书馆服务,建立诚信反馈、服务评估、优胜劣汰等机制,切实加强基层服务管理水平,提升标准化居村综合文化活动室(中心)终端服务质量。 图4 新样本数据T2图 3.3结果分析 由实验结果可以看出,在实时监控中rank图的监控效果比多元T2控制图好得多,这主要是因为多元T2控制图是基于分布参数的变化来检测变异的,因此对于每个时间点超限的响应情况并不灵敏。而rank图是直接基于对多元数据的由内而外的排序,对超限的情况响应速度很快而且显示结果很准确。 本文应用基于数据深度的rank图对发动机数据进行监控,结果表明,该控制图可以对多个发动机参数进行同时监控,可及时地发现多个参数中任意一个参数超限的情况,有效地提高观测效率,同时减少了单参数监测过程的失真情况。将该控制图与多元T2控制图的监控效果进行了对比,结果显示,在多元参数的实时超限监控中,rank图的监控效果远远优于多元T2控制图。 [1]孔成安,李文华,尹湛.利用QAR数据实施飞机性能监控[J].中国民用航空,2008(3):53-54. KongCheng’an,LiWenhua,YinZhan.ApplytheQARDatatoImplementMonitoringofAircraftPerformance[J].ChinaCivilAviation,2008(3):53-54. [2]林兆福,范作林,高海川.航空发动机状态监控和故障诊断软件[J].中国民航学院学报,1991,9(3):10-24. LinZhaofu,FanZuolin,GaoHaichuan.AeroEngineConditionMonitoringandFaultDiagnosisSoftware[J].JournalofChinaCivilAviationCollege,1991,9(3):10-24[3]FisherR.TheLogicofInductiveInference[J].JournaloftheRoyalStatisticalSociety,1935, 98(1):39-54. [4]EklundNH,GoebelKF.UsingNeuralNetworksandtheRankPermutationTransformationtoDetectAbnormalConditionsinAircraftEngines[C]//SoftComputinginIndustrialApplications.Montreal:IEEE, 2005: 1-5. [5]HinkleyDV.InferenceabouttheChange-pointinaSequenceofRandomVariables[J].Biometrika,1970,57(1): 1-17. [6]KimH.Change-PointDetectionforCorrelatedObservations[J].StatisticalSinica,1996,6: 275-287. [7]LowryCA,WoodallWH,ChampCW.MultivariateExponentiallyWeightedMovingAverageControlChart[J].Techno.Metrics,1992,34(1):46-53. [8]HuX,QiuH,IyerN.MultivariateChangeDetectionforTimeSeriesDatainAircraftEngineFaultDiagnostics[C]//Systems,ManandCybernetics, 2007.Montreal:IEEE, 2007: 2484-2489. [9]HotellingH.ThegeneralizationofStudent’sRatio[J].Ann.Math.Statist., 1931,2: 360-378. [10]LiuR.ControlChartsforMultivariateProcesses[J].JournalofAmericanStatisticsAssociation,1995,90:1380-1387. [11]LiuR.MonitoringMultivariateAviationSafetyDatabyDataDepth:ControlChartsandThresholdSystems[J].IIETransactions,2000,32(9):861-872.[12]LiuR.OnaNotionofDataDepthBasedonRandomSimplices[J].TheAnnalsofStatistics,1990, 18(1): 405-414. [13]张津.民用航空发动机状态监视和故障诊断系统研究[J].航空动力学报,1994,9(4):339-343. ZhangJin.CivilAviationEngineConditionMonitoringandFaultDiagnosisSystem[J].JournalofAerospacePower,1994,9(4):339-343. [14]朱建东.飞机发动机的监控技术及其发展趋势[J].飞机设计,2003(1):58-61. ZhuJiandong.MonitoringTechnologyandtheDevelopmentTrendsofAircraftEngine[J].AircraftDesign,2003(1):58-61. [15]蒋家东,蒋小琴.多元控制图的比较研究[J].航空标准化与质量,2007(1): 17-21. JiangJiadong,JiangXiaoqin.AComparativeStudyofMultivariateControlCharts[J].AviationStandardizationandQuality,2007(1):17-21. (编辑苏卫国) Applications of Nonparametric Multivariate Rank Chart to Aircraft Engine Monitoring Kong XiangfenZhang Bing Civil Aviation University of China,Tianjin,300300 Multiple monitoring of aircraft engine could solve the problems that the previous one-parameter monitoring detected so many parameters that the indicates will be distorted.TheT2control chart and the rank chart were applied simultaneously to monitor low-pressure rotor vibration value and high-pressure rotor vibration value for their real-time monitoring,and the performances of the two charts in aircraft engine real-time monitoring were compared and analyzed.The results show that the performance of rank chart is better than the T2control chart. data depth;rank chart;aircraft engine monitoring;T2control chart 2014-05-27 航空基金资助项目(20130267001) V263.6;F273.2DOI:10.3969/j.issn.1004-132X.2015.12.011 孔祥芬,女,1974年生。中国民航大学航空工程学院副教授。研究方向为质量管理。发表论文20余篇。张兵,男,1988年生。中国民航大学航空工程学院硕士研究生。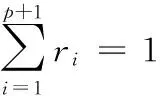
2 多元发动机参数数据监控
3 基于数据深度的rank图与经典多元控制图的比较
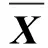
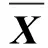
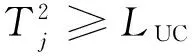

4 结语
