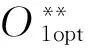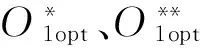浮动平底推杆-盘形凸轮组合机构的第Ⅰ类机构综合问题
2015-10-29林荣富李延平
常 勇 林荣富 李延平
集美大学,厦门,361021
浮动平底推杆-盘形凸轮组合机构的第Ⅰ类机构综合问题
常勇林荣富李延平
集美大学,厦门,361021

等距/网格/离散化;浮动坐标系;支撑函数;瞬时区域套;经济搜索区域;脊点/脊线
0 引言
2010~2012年,笔者以德国进口的高速印刷机机构为研究对象,提出浮动滚子推杆-盘形凸轮组合机构的Ⅰ、Ⅱ两类机构综合问题,对后者通过引入“瞬时、整程区间(域)套”、“浮动数轴、坐标系”、“最经济搜索带域”等一系列概念和“降维快速求解”的理论方法,取得了较系统的研究成果[1-3]。回过头来看,关于Ⅰ类机构综合问题,早在1991年即通过引入“虚拟摆杆”的新概念得到较为圆满的解决[4]。
随着研究的自然引伸和拓展,笔者又产生了如下设想:若将前述机构中的滚子以平底替代,对应的Ⅰ、Ⅱ两类机构综合问题的准确描述该如何给出?如何解决?
平底较之滚子,在承载能力、润滑特性、工作寿命、传动和高速性能等诸多方面具有显著优越性,自然也可以应用于高速印刷机机构场合。不难推想,研究解决上述引伸拓展性课题,具有机构学理论研究和工程实际应用两方面的重要意义。
2013年,我们在进行Ⅱ类综合问题准确描述的基础上,通过揭示出“瞬时一维直线区域”和“瞬时区间套”,提出求解平底方位线容许选择区域、凸轮基圆半径许用取值范围的基本原理等,解决了浮动平底推杆-盘形凸轮组合机构的第Ⅱ类机构综合问题[5]。
国内外已有许多学者以压力角为评价指标对平面盘形凸轮机构进行了尺寸综合[6-10],对做平面运动的滚子从动件凸轮机构的综合问题也作了相应研究[11-16]。
研究认为,浮动平底推杆-盘形凸轮组合机构Ⅰ类综合问题的准确描述如下:已知从动构件系统的运动学尺寸、输出件推/回程始终位置和(角)位移规律,推/回程许用压力角、平底位于连杆位置及与连杆夹角等条件,求解凸轮轴心许用区域、凸轮基圆半径r0许用取值范围等。
较之平底Ⅱ类、滚子Ⅰ类机构综合问题,平底Ⅰ类机构综合问题困难、复杂得多。滚子情形时,因任一瞬时滚子中心确定,故根据虚拟摆杆概念和类速度图原理,先求解任一瞬时凸轮轴心的位置区域,再通过求交得到整程凸轮轴心的位置区域,即可使综合问题得到解决。然而平底情形时,虽然任一瞬时平底位置确定,但凸轮、平底接触点即“瞬时滚子中心”不确定,导致任一瞬时的虚拟摆杆不确定,因此与类速度图原理无法顺利实现“链接”,从而导致“整程”凸轮轴心的位置区域无法求解确定。
与滚子情形“虚拟摆杆+类速度图”的求解原理不同,本文提出一种新颖的“预设凸轮轴心O1+等距/网格/离散化+校核+取舍”的求解思路、原理和方法,较为圆满地解决了浮动平底推杆-盘形凸轮组合机构的第Ⅰ类机构综合问题。
围绕“预设凸轮轴心O1+等距/网格/离散化+校核+取舍”的求解路线,通过建立“固定、浮动坐标系”,特别是通过引入“支撑函数法”、“瞬时区域套理论”、“经济搜索区域”等新概念和“等距/网格/离散化”方法,循序渐进地研究了满足ρ>0、α≤[α]∩α≤[α]r及ρ>0∩α≤[α]∩α≤[α]r(ρ为凸轮轮廓曲率半径,α为压力角,“∩”表示同时满足)等单纯、组合条件下凸轮轴心O1的求解原理、解析表达、“位置区域Πρ、Π[α]和Πρ∩[α]”及其形态特征,提出了搜索求解的思路、原理和方法,最后提出平底工作段及其长度、总长度的求解确定方法。

1 高速印刷机机构平底演化型第Ⅰ类机构综合问题的准确表述
图1所示为凸轮分别沿顺时针、逆时针转动的浮动平底推杆-盘形凸轮组合机构,由凸轮1、连杆2、摇块3、摇杆4和机架0等组成,凸轮1、摇杆4分别为输入件、输出件。实质上,该机构可视为德国进口高速印刷机机构[1-3]的演化型式。
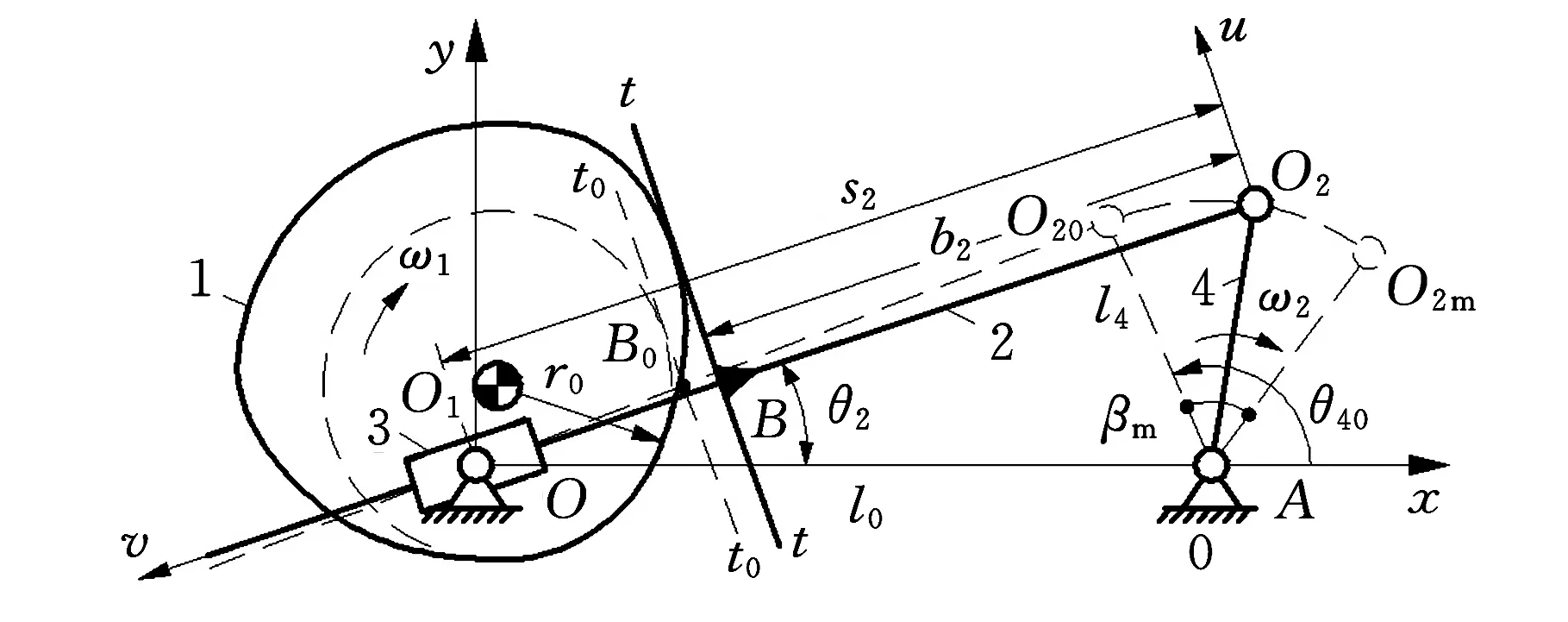
(a)凸轮顺时针转动

(b)凸轮逆时针转动图1 浮动平底推杆-盘形凸轮组合机构
图1所示的两机构的差异是凸轮分别沿顺时针、逆时针转动,其机构综合问题准确描述如下:
已知:机架和摇杆长度分别为l0、l4,t-t垂直于OO2,OO2与t-t的交点为B,O2与t-t间的距离为b2,摇杆的初位角为θ40、行程角为βm,摇杆推/回程位移规律分别为β=β(θ1)、βr=βr(θ1),推/回程运动角分别为Φ、Φr,推/回程许用压力角分别为[α]、[α]r。
求解:满足ρ>0、α≤[α]∩α≤[α]r条件的机构解集,即凸轮轴心O1的容许选择区域、凸轮基圆半径r0的许用取值范围等。
显而易见,上述机构综合问题属于第Ⅰ类机构综合问题。
2 预先准备工作
2.1固定坐标系建立和预备公式推导
建立固定直角坐标系Oxy,如图1所示。选取摇块轴心与原点O重合,x轴正向与OA方向一致,θ2、θ4分别为任一瞬时连杆、摇杆位置角,即OO2、AO2与x轴正向夹角,θ1为凸轮转角。
建立封闭矢量方程(略),连杆2的时变长度(s2、s20)、位置角(θ2、θ20)和类角速度(dθ2/dθ1)分别为
(1)
(2)
θ2=arctan{l4sin(θ40-β)/[l0+l4cos(θ40-β)]}
(3)
θ20=arctan[l4sinθ40/(l0+l4cosθ40)]
(4)
(5)
(6)
式中,xO2、yO2为O2点的x、y坐标。
据上可知,s2、θ2、dθ2/dθ1和xO2、yO2等皆为θ1的一元函数。
连杆2的绝对瞬心P20的坐标为
(7)
连杆2的相对瞬心P21的坐标为
(8)
式(8)中,“±”中的“+”表示适用于凸轮顺时针转动的推程前半区段和凸轮逆时针转动的推程后半区段,“-”则表示适用于凸轮顺时针转动的推程后半区段和凸轮逆时针转动的推程前半区段。
如图2所示,P21、P20两点和P21、O1(P10)两点间距离分别为
(9)
lP21P20、lP21O1皆是θ1的一元函数。下面将lP21P20简记为l21。
如图1所示,点B的坐标为
(10)
点B0的坐标为
(11)
s20、θ20可据式(2)和式(4)解得。
任一瞬时,t-t的方程为
cotθ2x+y-cotθ2xB-yB=0
(12)
推程起始瞬时,t0-t0的方程为
cotθ20x+y-cotθ20xB0-yB0=0
(13)
点(xk,yk)至t0-t0的距离为
d=|cotθ20xk+yk-cotθ20xB0-yB0|sinθ20
(14)
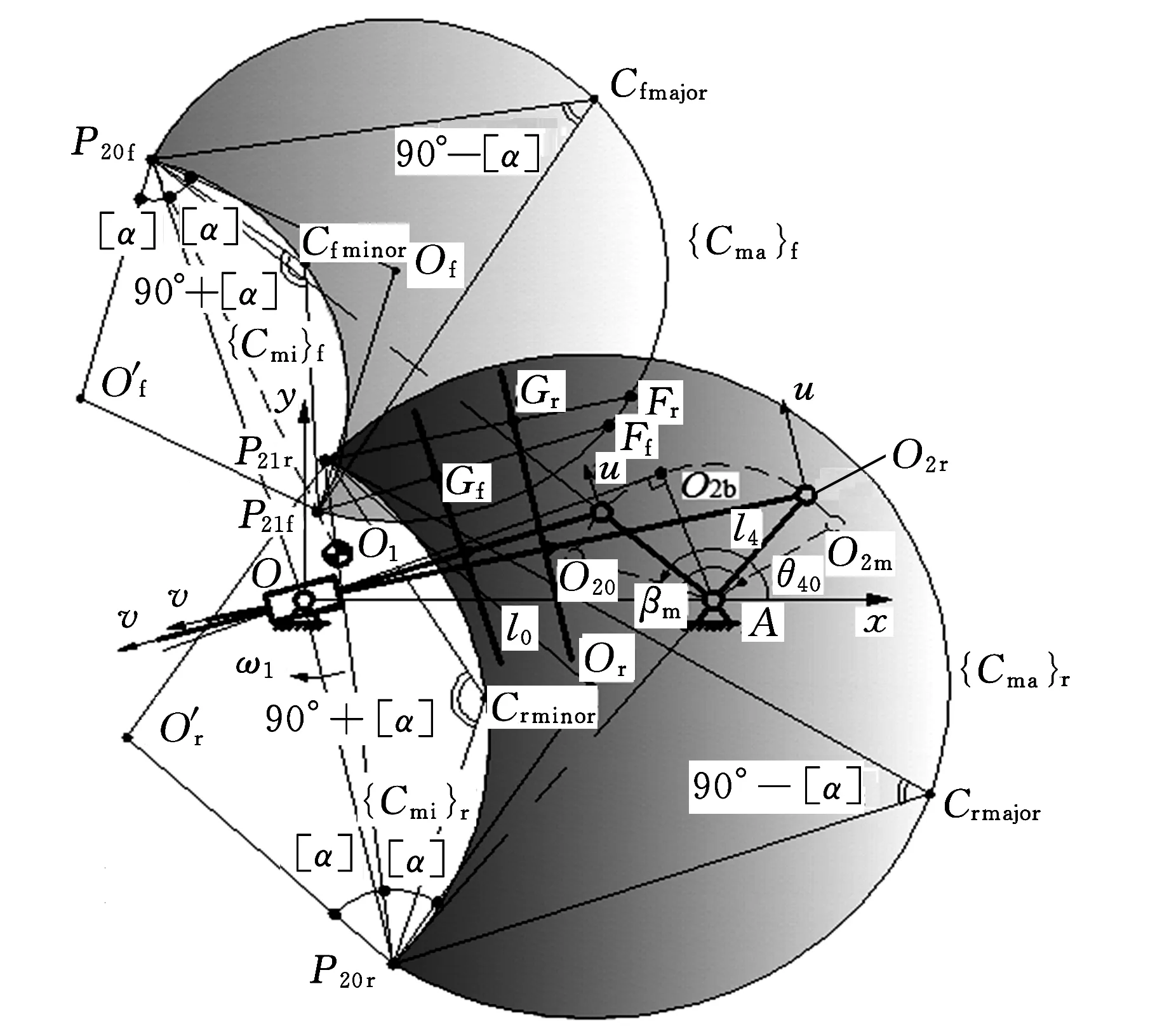
(a)推程

(b)回程图2 推程和回程前/后半区段划分和满足α≤[α]∩α≤[α]r条件的凸轮轴心O1的求解原理(凸轮顺时针转动情形)
2.2浮动坐标系O2u v的建立[2]
浮动坐标系指固连于连杆平面Σ2上,以O2为原点的直角坐标系O2uv。机构运动过程中,O2uv随连杆平面Σ2做平面运动即“浮动”,如图1所示。2.3推程前半/后半区段划分
如图2所示,P20、P21分别为推程时连杆2的绝对瞬心和相对瞬心,P10为凸轮1的绝对瞬心。
推程前半区段,摇杆4位于O20A、O2bA之间,P20位于OO2上方;推程后半区段,摇杆4位于O2bA、O2mA之间,P20位于OO2下方。分界点O2b满足O2bA⊥O2bO。此时,P20位于垂直于OO2的无穷远处。有
cos(180°-θ40+β*)=l4/l0
(15)
β*=arccos(l4/l0)+θ40-180°
(16)

2.4支撑函数法的预备知识[17]
2.4.1凸集的支撑线、支撑函数和方向角
设N为有界闭凸集,边界∂N为闭凸曲线,如图3所示。任选坐标系O1x′y′,自原点O1引射线O1R,且与x′轴正向夹角为φ(逆时针为正),作垂直于O1R且与N相交的任一直线G1(p1,φ),集合p1的上确界记为p,即
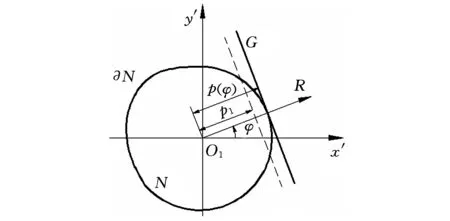
图3 支撑线、支撑函数与方向角
定义1与p对应的直线G(p,φ)称作凸集N沿φ方向的支撑线。
定义2与p对应的函数p(φ)称作凸集N沿φ方向的支撑函数。
定义3与p对应的角度φ称作支撑线G(p,φ)的方向角。
2.4.2凸集的充要条件
在边界曲线∂N适当定向下,凸集成立的充要条件是曲率半径ρ恒为正,即
ρ=p(φ)+p″(φ)>00≤φ<2π
(17)
3 满足ρ>0∩α≤[α]∩α≤[α]r条件的凸轮轴心O1的求解原理和解析表达
探索、建立满足ρ>0∩α≤[α]∩α≤[α]r条件的凸轮轴心O1的求解原理和解析表达,是本文的一个核心和难点所在。
3.1满足ρ>0条件的凸轮轴心O1的求解原理和解析表达
本文拟采用支撑函数法[7-8]来解决凸轮轮廓全部外凸即运动保真性问题。
3.1.1凸轮顺时针转动
3.1.1.1推程
如图4所示,OBO2A、OB0O20A分别为机构任一瞬时位置、推程起始瞬时位置,T、T0为对应的凸轮、平底接触点。
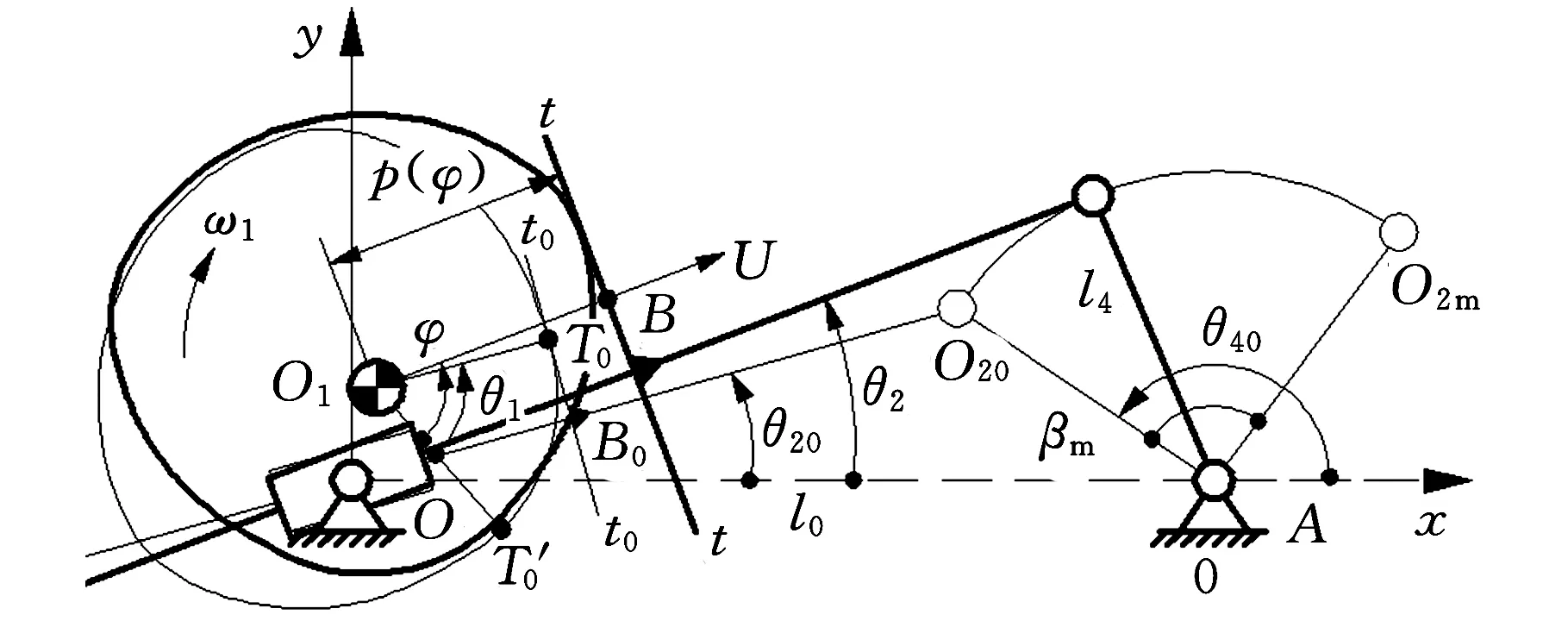
(a)凸轮顺时针转动
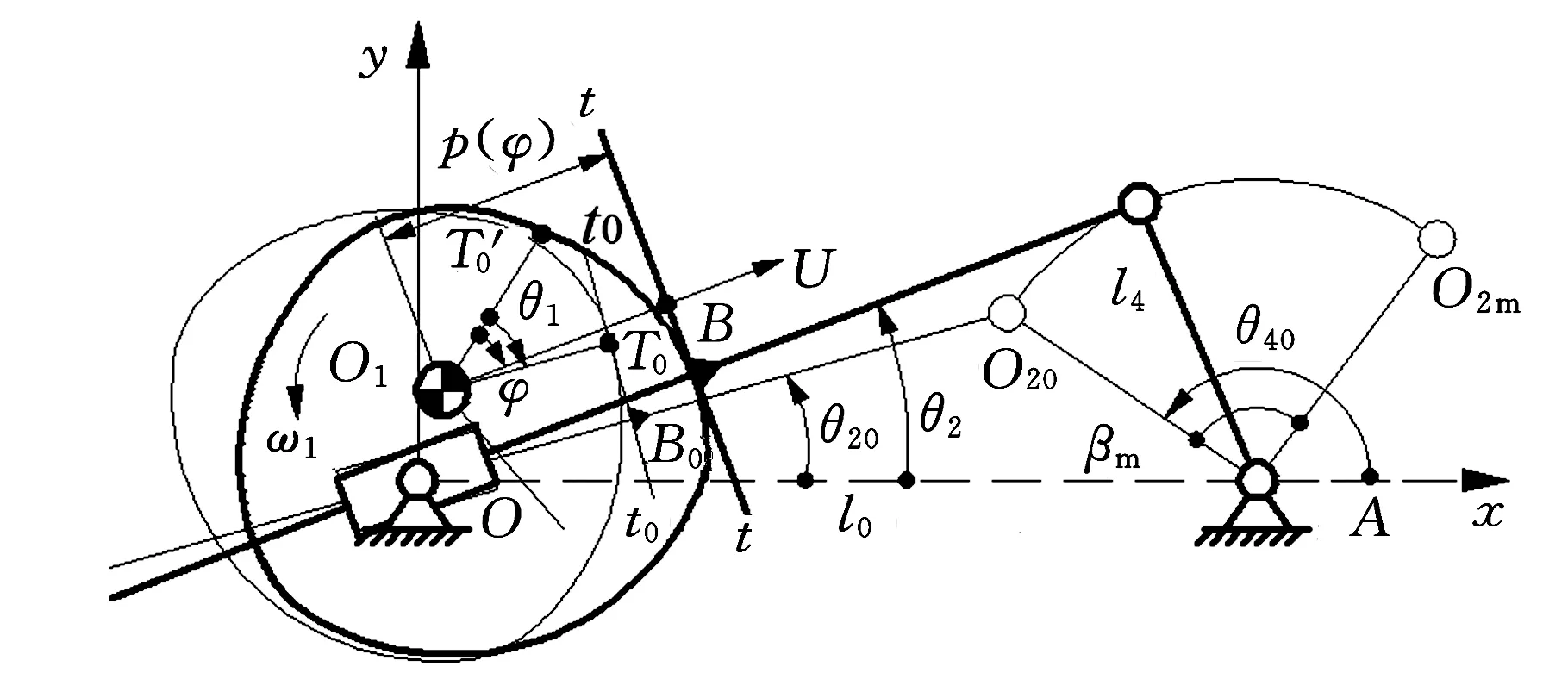
(b)凸轮逆时针转动图4 支撑函数、方向角的分析和提取

根据解析几何,点O1到t-t的距离为
O1T′=|cotθ2xO1+yO1-cotθ2xB-yB|sinθ2
(18)
支撑函数为
p(φ)=p(θ1)=O1T′=|cotθ2xO1+
yO1-cotθ2xB-yB|sinθ2
(19)
方向角为
φ=θ1+λ(θ2-θ20)
(20)
式中,λ为转向系数,凸轮顺时针转动时λ=1,逆时针转动时λ=-1。
将p(φ)对φ求一阶导数:
p′(φ)=dp(φ)/dφ=(dp(φ)/dθ1)/(dφ/dθ1)
(21)
令
D=dp(φ)/dθ1=d(O1T′)/dθ1=
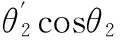
(22)
其中
|A|′=d|A|/dθ1=AA′/|A|
(23)
A=cotθ2xO1+yO1-cotθ2xB-yB
(24)
A′=(xB-xO1)θ2′csc2θ2-yB′-xB′cotθ2
(25)
(26)
(27)
(28)
(29)
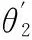
(30)
据式(21)~式(30),有

(31)
再将p(φ)对φ求二阶导数:
p″(φ)=d2p(φ)/dφ2=dp′(φ)/dφ=
(dp′(φ)/dθ1)/(dφ/dθ1)
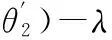
(32)
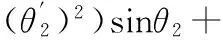
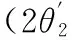
(33)
|A|″=d|A|′/dθ1=AA″/|A|
(34)
csc2θ2-y″B-x″Bcotθ2
(35)
(36)
(37)
(38)
据上,有
p″(φ)=dp′(φ)/dφ=
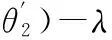
(39)
根据文献[18],对p(φ)和p″(φ)求和:
ρ=p(φ)+p″(φ)=|cotθ2xO1+yO1-
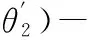
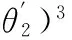
(40)
式(40)为预设凸轮轴心O1(xO1,yO1)时,凸轮轮廓曲率半径的通用解析计算公式。
据凸轮轮廓全部外凸的条件ρ>0,得
|cotθ2xO1+yO1-cotθ2xB-yB|sinθ2+
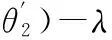
(41)
式(41)为预设凸轮轴心O1(xO1,yO1)时,机构的运动保真条件。
3.1.1.2回程
对于回程,式(18)~式(41)通用,不再赘述。
3.1.2凸轮逆时针转动
与3.1.1同理,从略。
3.2满足α≤[α]∩α≤[α]r条件的凸轮轴心O1的求解原理和解析表达
3.2.1凸轮顺时针转动(图2)
3.2.1.1推程(图2a)
将整个推程划分为推程前半区段、后半区段[1-2]进行分析。
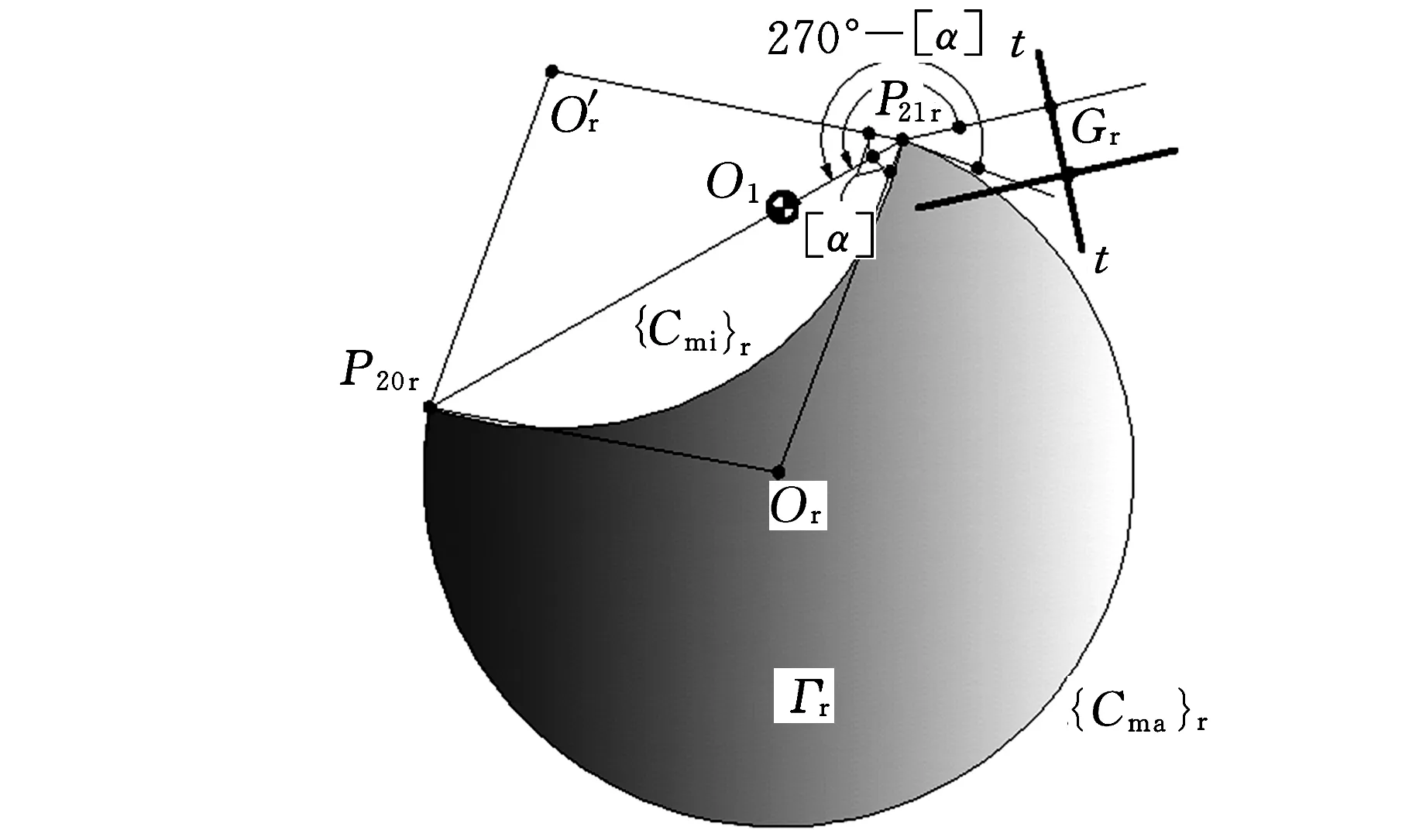
如图2a所示,任一瞬时位置,在连杆平面Σ2上,以P20P21为弦、朝O2v轴负向作优弧{Cma}、劣弧{Cmi},使其满足
∠P20CmajorP21=90°-[α]
(42)
∠P20CminorP21=90°+[α]
(43)
根据文献[2],浮动滚子推杆机构在该瞬时满足α≤[α]条件的滚子中心点的全集为“瞬时区域套”Γ(u,v),即由{Cma}、{Cmi}合作围成的“盈月形”二维平面区域(图2阴影部分)。
过P21引t-t的垂线P21G,得垂足G,G即为该瞬时凸轮、平底接触点,同时可能得到与{Cmi}、{Cma}的交点E和F。分别选取P21G、P21P20为∠GP21P20的始边、终边,则有
∠GP21P20=∠xP21P20-∠xP21G
(44)
式中,∠xP21G和∠xP21P20分别为始边P21G、终边P21P20的倾斜角,即有向线段P21G、P21P20沿逆时针与x轴正向的夹角。
特别规定:∠GP21P20沿逆时针方向量取计算,恒为正。理论上,∠GP21P20取值域为
∠GP21P20∈[0,360°)
(45)
根据对象机构的特殊性,恒有
∠xP21G=θ2<90°
(46)
即∠xP21G恒为锐角。
设
ζ=arctan((yP20-yP21)/(xP20-xP21))
(47)
其取值域为ζ∈(-90°,90°)。对应地,∠xP21P20的计算方法有如下3种情况:①xP20-xP21>0、yP20-yP21≥0时,若ζ≥θ2,则∠xP21P20=ζ;若ζ<θ2,则∠xP21P20=360°+ζ;②xP20-xP21<0、yP20-yP21>0时和xP20-xP21<0、yP20-yP21<0时,∠xP21P20=180°+ζ;③xP20-xP21>0、yP20-yP21<0时∠xP21P20=360°+ζ。
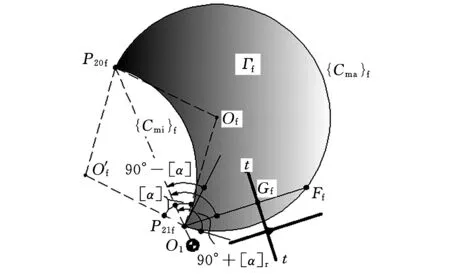
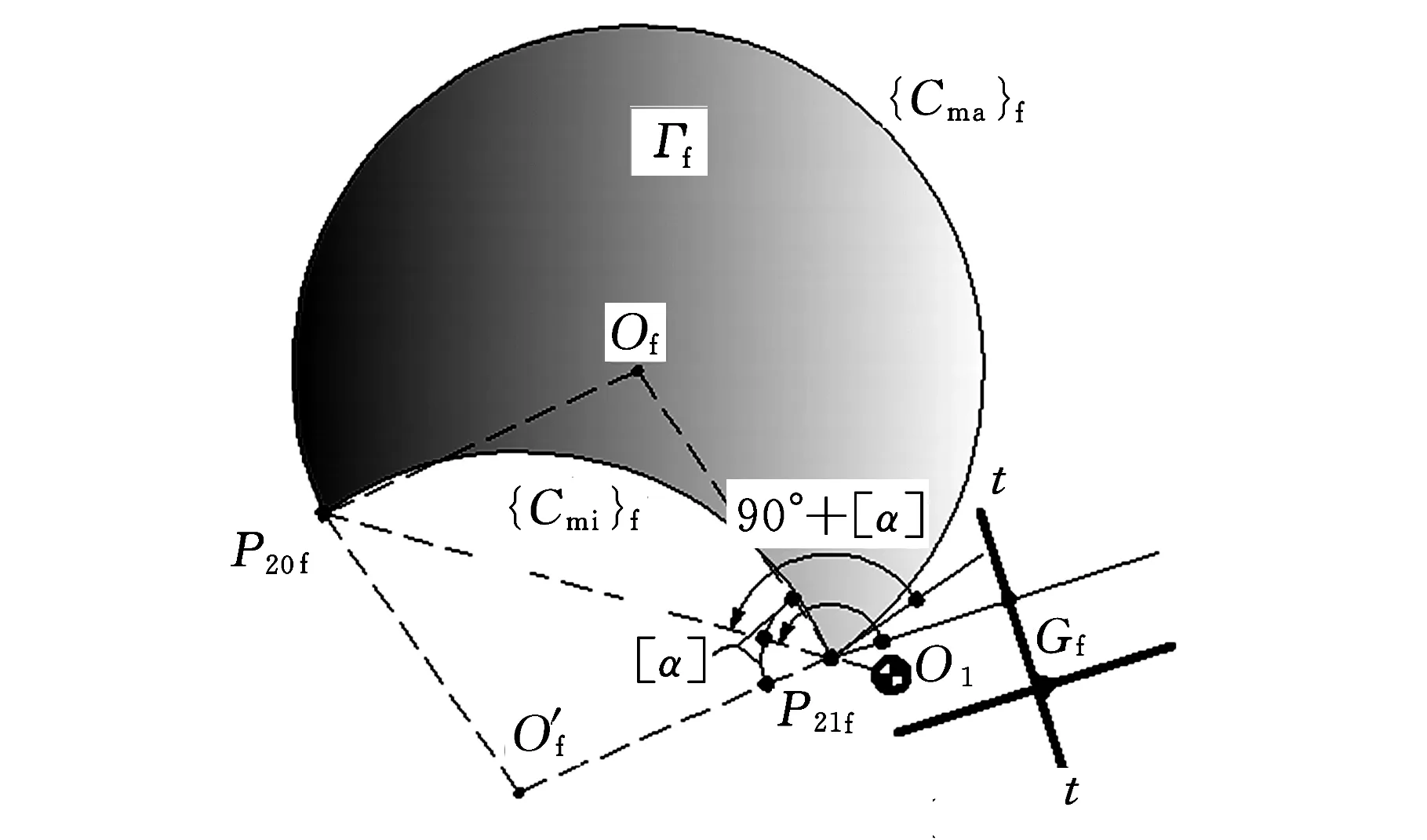
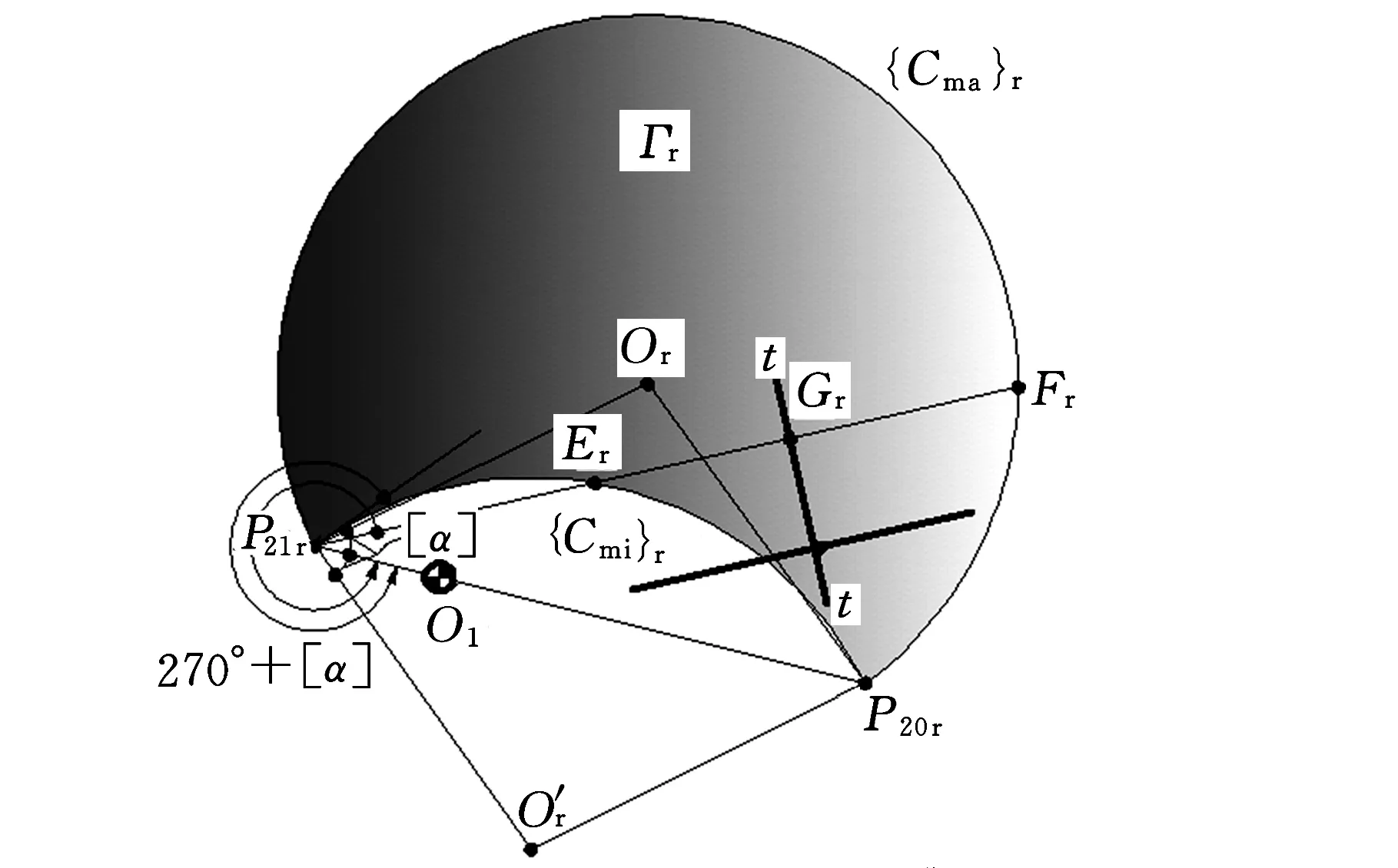
(1)推程前半区段(图2a)。推程前半区段,P21f位于P20f、O1(P10)之间,如图2a所示,此时垂足Gf与瞬时区域套Γf(u,v)的相对位置存在下述三种可能情况(图5):
①0°≤∠GfP21fP20f<90°-[α](图5a),即Ef、Ff(Ef、Ff为Gf与瞬时区域套Γf(u,v)的两交点)皆存在。在ΔGfP21fP20f中,据正弦定理,有
P21fEf=f1(θ1)=
l21|cos([α]+η∠GfP21fP20f)|/cos[α]
(48)
P21fFf=f2(θ1)=
l21|cos([α]-η∠GfP21fP20f)|/cos[α]
(49)
式中,η为区段系数,推程前半区段η=1,后半区段η=-1。
根据点到直线距离公式[5],任一瞬时P21f到tf-tf的距离为
P21fGf=f3(θ1)=
|cotθ2xP21+yP21-cotθ2xB-yB|sinθ2
(50)
据式(48)~式(50)知,P21fEf、P21fFf和P21fGf即f1(θ1)、f2(θ1)和f3(θ1)皆为θ1的一元函数。
上述情况又分为两种情况:
a.P21fEf≤P21fGf≤P21fFf即f1(θ1)≤f3(θ1)≤f2(θ1),此时Gf位于Γf(u,v)内部,满足α≤[α]条件。该情况下,若P21fEf b.P21fGf ②90°-[α]≤∠GfP21fP20f≤90°+[α](图5b),即Ff存在、Ef不存在,此时式(50)通用。此情况又分为两种情况: a.P21fGf≤P21fFf即f3(θ1)≤f2(θ1),此时Gf位于Γf(u,v)内部,满足α≤[α]条件。该种情况下,若P21fGf b.P21fGf>P21fFf即f3(θ1)>f2(θ1),此时Gf位于Γf(u,v)外部,不满足α≤[α]条件。 ③90°+[α]<∠GfP21fP20f<360°(图5c),即Ef、Ff皆不存在,此时G位于Γ(u,v)外部,不满足 (a)Ff存在,Ef存在 (b)Ff存在,Ef不存在 (c)Ff不存在,Ef不存在图5 推程前半区段Gf与Γf(u,v)相对位置 α≤[α]条件。 (2)推程后半区段(图2b)。推程后半区段,P21r位于P20r、O1(P10)延长线上,如图2b所示。此时Gr与Γr(u,v)的相对位置亦存在三种可能情况(图6): (a)Fr存在,Er存在 (b)Fr存在,Er不存在 (c)Fr不存在,Er不存在图6 推程后半区段Gf与Γf(u,v)相对位置 ①270°+[α]<∠GrP21rP20r≤360°(图6a),此时Er、Fr(Er、Fr为Gr与瞬时区域套Γr(u,v)的两交点)皆存在,式(48)~式(50)通用,不过,式(48)和式(49)中,η=-1。该情况又分为两种情况: a.P21rEr≤P21rGr≤P21rFr,此时Gr位于Γr(u,v)内部或{Cmi}r、{Cma}r上,满足f1(θ1)≤f3(θ1)≤f2(θ1),该瞬时满足α≤[α]条件。 b.P21rGr ②270°-[α]≤∠GrP21rP20r≤270°+[α](图6b),即Fr存在、Er不存在,式(50)通用。该情况又分为两种情况: a.P21rGr≤P21rFr,即Gr位于Γr(u,v)内部或{Cma}r上,满足f3(θ1)≤f2(θ1),该瞬时满足α≤[α]条件。 b.P21rGr>P21rFr,即Gr位于Γr(u,v)外部,满足f3(θ1)>f2(θ1),该瞬时不满足α≤[α]条件。 ③0°<∠GrP21rP20r<270°-[α](图6c),即Er、Fr皆不存在,此时Gr位于Γr(u,v)外部,不满足α≤[α]条件。 综上所述,得到重要结论:推程任一瞬时,若属于①a情况或②a情况,则该瞬时满足α≤[α]条件;反之,该瞬时不满足α≤[α]条件。 推延、归纳之,得到重要结论:整个推程所有瞬时,无论前半区段还是后半区段,若皆属①a情况或②a情况,则为满足α≤[α]条件的凸轮轴心O1;反之,为不满足α≤[α]条件的凸轮轴心O1。上述“反之”表示“只要某一瞬时不属于①a情况或②a情况”之意。 3.2.1.2回程 绝大多数情况下,因为[α]r∈(70°,80°),回程时α≤[α]r条件通常可获得自然满足,故回程一般可免予考虑。 3.2.2凸轮逆时针转动(图4b) 与3.2.1节类似,从略。 如何在“漫无边界”的机架平面Σ0上挖掘、揭示出满足ρ>0∩α≤[α]∩α≤[α]r条件的凸轮轴心O1的位置区域,是本文的另外一个关键和难点所在。 4.1“经济搜索区域”的概念及其等距/网格/离散化 显然,t0-t0将整个机架平面Σ0划分为左半平面Σ0L和右半平面Σ0R。因凸轮推平底运动,故凸轮轴心O1仅可能位于t0-t0为边界的平面Σ0L上,不可能位于t0-t0为边界的平面Σ0R上。 如图7所示,绝对瞬心线{P20}由{P20}up和{P20}un上下两分支构成,分别对应推程前半区段和后半区段。 图7 满足ρ>0条件的凸轮轴心O1的位置区域 研究发现,与推程始点、终点瞬时对应的绝对瞬心P20S、P20E分别位于{P20}up、{P20}un的最低点、最高点,即 (51) 根据上述分析,提出并认定凸轮轴心O1必位于如下“经济搜索区域Ω”内: (52) 式中,xt0为t0-t0上点的x坐标;yP20S、yP20E分别为P20S和P20E的y坐标。 式(52)的隐性涵义是:t0-t0为边界的左半平面Σ0L的y=yP20S以下、y=yP20E以上两子区域的所有点,皆属3.2节的情况①b、②b或情况③。证明从略。 不言而喻,经济搜索区域Ω是有限区域,左半平面是无限区域,前者是后者的子区域。显而易见,经济搜索区域Ω呈现梯形的形态特征。 经济搜索区域Ω的提出,在确保O1位置区域完整、无缺失前提下,大大缩小了搜索范围,显著提高了求解效率。 现在,对经济搜索区域Ω进行等距、网格、离散化处理,具体步骤如下: (1)以y=0(横轴)为基准,分别朝上、朝下作等距、离散平行的直线族{yj},其方程为 y=yj=jΔyj=jmin,…,-1,0,1,…,jmax (53) 且有 jmax=ent(yP20S/Δy) (54) jmin=ent(yP20S/Δy) (55) 式中,Δy为相邻两直线y=yj、y=yj+1间的距离。 (2)以x=0(纵轴)为基准,分别朝左、朝右作等距、离散平行直线族{xi},其方程为 x=xi=iΔxi=imin,…,-1,0,1,…,imax (56) 且有 imax=ent(xt0/Δx) (57) imin=ent(-l0/Δx) (58) 式中,Δx为相邻两直线x=xi、x=xi+1间距离。 (3)正交单元网格的边长为 Δx=Δy=10-p(mm) (59) 式中,p=1,2,…,根据精度要求确定。 通过等距、网格、离散化处理后,Ω由连续、无数点转化为离散、有限点的网格节点族{(xi,yj)},如图7所示。(xi,yj)即表示两直线x=xi、y=yj相交得到的任一网格节点。 4.2满足ρ>0条件的凸轮轴心O1的位置区域及其形态特征 4.2.1凸轮顺时针转动 对于网格节点族{(xi,yj)},自y=yjmin到y=yjmax逐层、各层自x=ximax到x=ximin逐节点作遍历性计算,校核推程、回程是否皆满足运动保真条件,若满足,则将点{(xi,yj)}保存,否则舍弃。于是,可得到满足ρ>0条件的凸轮轴心O1的位置区域Πρ即网格节点集合{(xi,yj)}ρ>0。 大量案例计算表明:位置区域Πρ为有一条朝 左开放边界∂Πρ的解区域,如图7所示。 4.2.2凸轮逆时针转动 同理,从略。 4.3满足α≤[α]∩α≤[α]r条件的凸轮轴心O1的位置区域及其形态特征 4.3.1凸轮顺时针转动 同4.2.1节,自y=yjmin到y=yjmax逐层、各层自x=ximax到x=ximin逐节点作遍历性计算,校核整个推程是否皆满足运动保真条件,若皆满足运动保真条件则保存{(xi,yj)};否则舍弃之。于是,得到满足α≤[α]∩α≤[α]r条件的凸轮轴心O1的位置区域Π[α]即网格节点集合{(xi,yj)}α≤[α]。 根据大量案例的求解计算,得到如下重要结论: (1)位置区域Π[α]的形态特性。Π[α]具有类似等腰三角形的形态特征。上下两腰HI、HJ和底边IJ(在t0-t0上)构成边界∂Π[α],如图8所示。 图8 满足α≤[α]∩α≤[α]r条件的凸轮轴心O1的位置区域 若记顶点为H[α](x[α]a,y[α]a),则有x[α]a=min{xi}Π[α],min{xi}Π[α]为Π[α]中所有网格节点x坐标的最小者。 对于两腰HI、HJ上的点,有α=[α];而对于底边IJ上的点,有α≠[α]。对于上腰HI,从H到I诸点,基圆半径r0呈单调递减变化,在I处取得最小值。对于下腰HJ,从H到J诸点,基圆半径r0亦呈单调递减变化,在J处取得最小值。 根据图8,有r0I>r0J,故满足α=[α]条件时有r0J=min{r0[α]},min{r0[α]}为满足α=[α]条件的所有凸轮轴心O1的凸轮基圆半径。 (2)Π[α]、∂Π[α]的收缩聚敛特性。取不同[α]值,对应得到Π[α]1、Π[α]2和Π[α]3,若[α]3≤[α]2≤[α]1,则Π[α]1⊂Π[α]2⊂Π[α]3,∂Π[α]1⊂∂Π[α]2⊂∂Π[α]3,表明:随[α]值减小,Π[α]、∂Π[α]不断收缩,[α]小者恒嵌套于大者内部。 cotθ20x+y-cotθ20xB0-yB0+cscθ20kΔt=0 (60) k=1,2,…,kmax 其中,Δt为相邻两直线tk-tk、tk+1-tk+1间距离,考虑到与前面Δx、Δy匹配,亦取Δt=10-p(mm)且有kmax=ent(yP20S/Δt)。 取直线tk-tk上任一点为凸轮轴心O1,则其具有相同的基圆半径r0k,且有 r0k=lk=kΔtk=1,2,…,kmax (61) 在直线族{tk-tk}(k=1,2,…,kmax)中任取一条直线tk-tk,分别与∂Π[α]1、∂Π[α]2截交各得两个交点D[α]1up、D[α]1un和D[α]2up、D[α]2un,显然[D[α]2un,D[α]2up]⊂[D[α]1un,D[α]1up]。 (62) 以[α]为变量进行一维搜索,直至得到[α]k,若记与之对应的Π[α]k的顶点为H[α]k(x[α]ka,y[α]ka),则据式(14),满足 |cotθ20x[α]ka+y[α]ka-cotθ20xB0-yB0|sinθ20-kΔt=0 (63) 4.3.2凸轮逆时针转动 同理,从略。 4.4满足ρ>0∩α≤[α]∩α≤[α]r条件的凸轮轴心O1的位置区域及其形态特征 4.4.1凸轮顺时针转动 4.4.1.1位置区域Πρ∩[α]的形态特征 基于4.2节和4.3节,得到交集 {(xi,yj)}ρ>0∩α≤[α]= {(xi,yj)}ρ>0∩{(xi,yj)}α≤[α] (64) 该交集即是满足ρ>0∩α≤[α]∩α≤[α]r条件的位置区域Πρ∩[α]。 如图9所示,位置区域Πρ∩[α]呈现组合、封闭的形态特征。 图9 满足ρ>0∩α≤[α]∩α≤[α]r条件的凸轮轴心O1的位置区域 具体说来,凸轮轴心O1的位置区域仍具有类三角形的区域形态特征。三个顶点分别是H[α]、I∩和J∩。I∩和J∩就是∂Πρ与∂Π[α]截交得到的两个交点。 4.4.1.2凸轮轴心O1的优选(非劣)解集 证明从略。 值得指出的是,4.4.1.2~4.4.1.4节选择凸轮轴心O1仅考虑了r0和α两个性能参数,存在片面、偏颇之处。工程实际中,除考虑r0和α外,还须兼顾考虑平底工作段分布,以及机构横向、纵向尺寸的合理分配等。不难想象,后两者对机构的运动平稳性、动力学特性以及运动空间等皆会产生重要影响。 4.4.2凸轮逆时针转动 求解方法与凸轮顺时针转动情形类似,不再赘述。 5.1浮动平底工作段的求解确定 平底工作段指机构整程中浮动平底与凸轮轮廓实际接触的区段。 5.1.1凸轮顺时针转动 如图2a所示,OBO2A为机构处于任一瞬时的位置。P21G的方程为y-yP21=tanθ2(x-xP21),xP21、yP21可据式(7)、式(8)算得。 将P21G的方程y-yP21=tanθ2(x-xP21)与式(18)联立,解得凸轮、平底接触点G在固定系Oxy中的坐标为 (65) xB、yB可据式(11)算得。 根据坐标变换原理,得G在浮动系O2uv中的坐标: (66) xO2、yO2可据式(6)算得。 由式(66)可知,uG是θ1的一元函数,vG是常值。 综合考虑推程、回程,一维搜索解得uG的最大和最小值分别为uGmax和uGmin,从而解得平底工作段uG∈[uGmin,uGmax]。 5.1.2凸轮逆时针转动 同理,从略。 5.2浮动平底工作段长度、总长度的求解确定 5.2.1凸轮顺时针转动 平底工作段长度为l=uGmax-uGmin,平底总长度为L=l+(5~7)mm。 5.2.2凸轮逆时针转动 同理,从略。 解: (1)据已知条件特别是第3、第4章求解理论方法,取p=2,通过编程搜索求解,解得凸轮轴心位置区域Πρ∩[α],如图9所示。也就是说,图9是据例题已知条件数据,通过计算机搜索求解自动生成的。 [1]常勇,杨富富.作平面运动滚子从动件盘形凸轮机构的第Ⅱ类机构综合问题[J].机械工程学报,2010,46(21):37-41. ChangYong,YangFufu.SecondMechanismSynthesisTaskofDiscCamMechanismswithRollerFollowerMovinginPlanarGeneralMotion[J].JournalofMechanicalEngineering,2010,46(21):37-41. [2]常勇,杨富富,李延平,等.作平面运动滚子从动件盘形凸轮机构的广义第Ⅱ类机构综合问题[J].机械工程学报,2012,48(15):47-57. ChangYong,YangFufu,LiYanping.ResearchonSecondMechanismsSynthesisTaskofPositive-driveDiscCamMechanismswithRollerFollowerMovinginGeneralPlanarMotion[J].ChineseJournalofMechanicalEngineering,2012,48(15):47-57. [3]常勇,杨富富.作平面运动滚子从动件形锁合凸轮机构的第Ⅱ类机构综合问题[J].机械工程学报,2012,48(1):39-46. ChangYong,YangFufu.SecondMechanismsSynthesisTaskofPositive-driveDiscCamMechanismswithRollerFollowerMovinginGeneralPlanarMotion[J].ChineseJournalofMechanicalEngineering,2012,48(1):39-46. [4]常勇,李延平,刘国祥.按许用压力角设计最小尺寸作平面复杂运动滚子从动件平面凸轮机构的解析法[J].机械工程学报,1991,27(4):37-41. ChangYong,LiYanping,LiuGuoxiang.TheAnalyticsforDesigningMinimumSizeDiscCamMechanismsWhoseRollerFollowerMovinginGeneralPlanarMotionaccordingtoAllowablePressureAngle[J].ChineseJournalofMechanicalEngineering,1991,27(4):37-41. [5]常勇,林荣富,李延平.作平面运动平底从动件盘形凸轮机构第Ⅱ类机构综合[J].农业机械学报,2013,44(7):286-292. ChangYong,LinRongfu,LiYanping.ClassⅡSynthesisofDiscCamMechanismwithFlat-facedFollowerinPlanarMotion[J].TransactionsoftheChineseSocietyforAgriculturalMachinery,2013,44(7):286-292. [6]常勇,林荣富,李延平.做平面运动滚子从动件盘形凸轮机构的深度广义第Ⅱ类综合问题[J].中国机械工程,2014,25(16):2149-2158. ChangYong,LinRongfu,LiYanping.GeneralClassⅡSynthesisofDiscCamMechanismwithRollerFollowerMovinginPalnarGeneralMotion[J].ChinaMechanicalEngineering,2014,25(16):2149-2158. [7]马喜川, 常勇, 李延平. 支撑函数在机构学中的若干重要应用[J].机械设计, 1996, 13(10): 24-26. MaXichuan,ChangYong,LiYanping.TheSeveralImportantApplicationsofSupportFunctioninMechanisms[J].JournalofMachineDesign,1996,13(10):24-26. [8]SchoenherrJ.SynthesisofPlanarCamMechanicswithLowestDimensions[J].MechanismandMachineTheory,1993,28(3):317-325. [9]NavarroO,WuCJ,AngelesJ.Size-minimizationofPlanarCamMechanisms[J].MechanismandMachineTheory,2001,36(3):371-386. [10]DasguptaA,GhostA.OntheDeterminationofBasicDimensionsofaCamwithaTranslatingRoller-Follower[J].JournalofMechanicalDesign,Trans.ASME,2004,126(1):143-147. [11]CarraS,GarzieraR,PellegriniM.SynthesisofCamswithNegativeRadiusFollowerandEvaluationofthePressureAngle[J],MechanismandMachineTheory,2004,39:1017-1032. [12]JiZ,MannaYA.SizeMinimizationofDiscCamswithRoller-followersunderPressureAngleConstraint[J].MechanicalEngineeringScience,Imeche,2008,222(12):2475-2484. [13]华大年.按许用压力角设计最小尺寸的摆动从动杆平面凸轮机构的解析法[J].机械工程学报,1982,18(4):74-79.HuaDanian.TheAnalyticsforDesigningMinimumSizeDiscCamMechanismswithOscillatingFolloweraccordingtoAllowablePressureAngle[J].ChineseJournalofMechanicalEngineering,1982,18(4):74-79. [14]常勇,吴从炘,李延平.关于《按许用压力角设计最小尺寸的摆动从动杆平面凸轮机构的解析法》一文的两点注记[J].黑龙江商学院学报(自然科学版),1989,5(2):49-54. ChangYong,WuCongxin,LiYanping.TheFurtherNoteson“theAnalyticsforDesigningMinimumSizeDiscCamMechanismswithOscillatingFolloweraccordingtoAllowablePressureAngle”[J].JournalofHeilongjiangCommercialCollege,1989,5(2):49-54. [15]王知行,李瑰贤.关于直动滚子从动件盘形凸轮基本尺寸的讨论[J].机械工程学报,1986,22(4):88-93. WangZhixing,LiGuixian.DiscussiononFundamentalSizeofTranslatingFollowerDiscCamMechanisms[J].ChineseJournalofMechanicalEngineering,1986,22(4):88-93. [16]吕庸厚,沈爱红.组合机构设计与应用[M].北京:机械工业出版社,2008. [17]吴家钦,奚定华.平面解析几何[M].上海:上海科学技术出版社,1982. [18]任德麟.积分几何学引论[M].上海:上海科学技术出版社,1988. (编辑苏卫国) Class Ⅰ Synthesis of Cam Mechanism with Floating Flat Faced Pushrod Chang YongLin RongfuLi Yanping Jimei University,Xiamen,Fujian,361021 equidistant/grid/discretization;floating coordinate system;support function;instantaneous area set;economic searching area;ridge point/ridge line 2013-11-14 2015-04-15 国家自然科学基金资助项目(51175224);福建省自然科学基金资助项目(2010J01302,2006J0169) TH112.2DOI:10.3969/j.issn.1004-132X.2015.12.004 常勇,男,1964年生。集美大学机械工程学院教授。研究方向为凸轮与连杆机构学、机构的起源与进化理论等。发表论文160篇。林荣富,男,1987年生。集美大学机械工程学院助教。李延平(通信作者),女,1963年生。集美大学机械工程学院教授。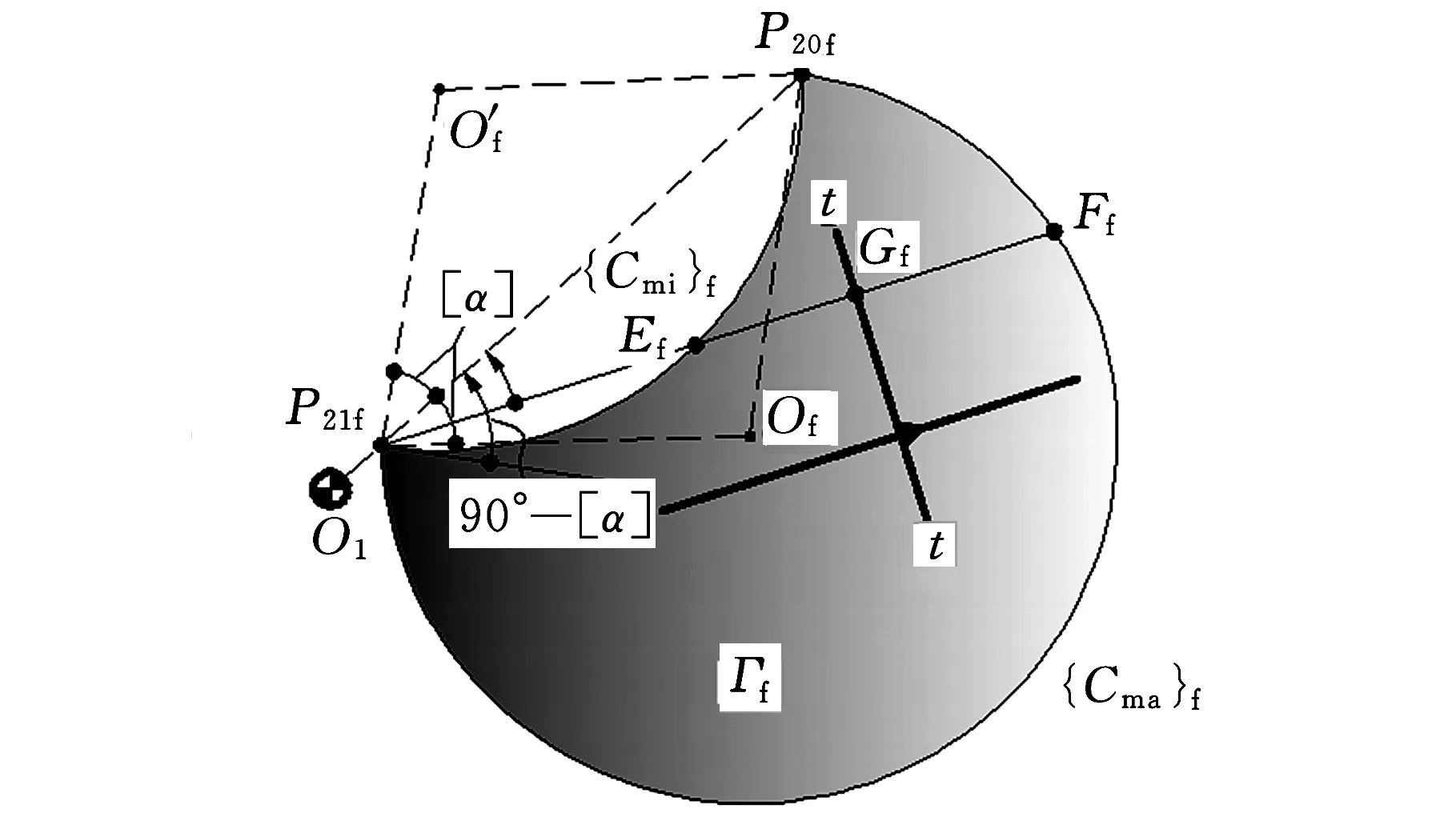

4 凸轮轴心O1的位置区域及其形态特征









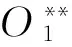


5 浮动平底工作段及其长度、总长度的求解确定
6 机构综合示例