海洋经济历史数据推算方法研究

李琳琳，宋维玲，郑莉，林香红，蔡大浩

（国家海洋信息中心，天津300171）

【统计与分析】

海洋经济历史数据推算方法研究

李琳琳，宋维玲，郑莉，林香红，蔡大浩

（国家海洋信息中心，天津300171）

海洋经济日益受到社会各界的关注，而海洋统计数据的积累是一个长期的过程，在海洋经济分析研究过程中，有必要对海洋经济的历史数据进行推算，以延长海洋经济数据时间序列，满足计量分析对数据的需要。在研究实践中，总结了比重法、灰色—周期外延组合模型、趋势外推法、指数平滑法等适用于海洋经济分析的历史数据推算方法，提出了各种方法的适用条件，并进行了实证分析。实证结果显示，根据指标数据实际情况选用适当方法能够较好推算海洋经济历史数据，但各推算方法只适用于个别指标缺少少量数据的情景，且可采用多种方法组合的形式进行历史数据推算。

海洋经济；海洋统计；推算方法

1　问题的提出

21世纪被称为海洋世纪，加强海洋的开发、利用、安全，关系到国家的安全和长远发展。随着陆地资源的枯竭和科学技术的发展，海洋资源的开发利用日益受到社会各界的重视，海洋经济逐渐成为学者们研究的热点。但是由于海洋经济统计核算起步较晚，统计核算体系尚不健全，许多海洋经济数据序列较短，给海洋经济的深入分析研究带来了困难，无法满足经济分析和决策的需要。由于缺少连续的长时间序列数据，许多宏观经济和计量经济的研究方法的应用受到限制。而统计数据的丰富和完善是一个长期的过程，因此在海洋经济研究过程中，如果个别指标缺少少量数据，根据研究需要可采用一定的方法对海洋经济历史数据和缺失数据进行推算，缓解海洋经济数据序列较短的问题。

海洋经济历史数据的推算有一定的数据基础：一方面国民经济统计数据比较丰富，有一些与海洋经济密切相关；另一方面尽管海洋经济起步较晚，但也有二十多年的积累，可以发现数据的变化规律。本文在研究实践中，总结提出了适用于海洋经济历史数据和缺失数据推算的方法与适用条件，并进行了实证分析，以期对相关研究有所裨益。

2　海洋经济历史数据推算方法

通过对比分析和实践验证，适用于海洋经济历史数据和缺失数据的推算方法主要有：比重法、灰色—周期外延组合模型、趋势外推法、指数平滑法。其中比重法是使用相关指标历史数据推算海洋经济指标历史数据，而灰色—周期外延组合模型、趋势外推法、指数平滑法皆是利用现有海洋经济指标数据的趋势、周期推算自身的历史数据。

2.1比重法

比重法，顾名思义是利用海洋经济指标所占比重推算其历史数据的方法。海洋经济是国民经济的重要组成部分，很多海洋经济指标是国民经济指标的一部分，而国民经济指标数据较多且序列较长。当比重相对稳定时，采用相近年份比重平均值与国民经济相应指标数据的乘积作为海洋经济相关指标的推算值；当比重可以运用模型很好拟合预测时，首先拟合比重并推导计算出比重的历史数据，然后采用推导计算得到的比重与国民经济相应指标数据的乘积作为海洋经济相关指标的推算值。比重法使用Excel软件便可以实现。

2.2灰色—周期外延组合模型

灰色—周期外延组合模型将灰色系统模型及周期外延模型组合起来，不仅能够反映指标序列的总体变化趋势，而且能够很好反映其周期波动的特点。灰色—周期外延组合模型的建模思想是首先建立序列的灰色GM（1，1）模型，然后，对剩余序列建立周期外延预测模型，作为灰色GM（1，1）模型的残差补偿。

灰色—周期外延组合模型推算海洋经济历史数据的具体计算步骤如下［1］：设海洋经济指标数据序列（非负）为：

1）建立序列x（0）（k）的灰色GM（1，1）模型：

①对原始数列作一次累加生成：

式中：k=1，2，…，n；xˆ（0）（1）=x（0）（1）。

2）求残差数列x′（k）：

3）建立剩余数列x′（k）的周期外延预测模型：

①计算序列x′（k）的均值生成函数：

式中：1≤m≤M，nm为小于n/m的最大整数；M为小于n/2的最大整数。于是得到一个均值生成函数矩阵为：

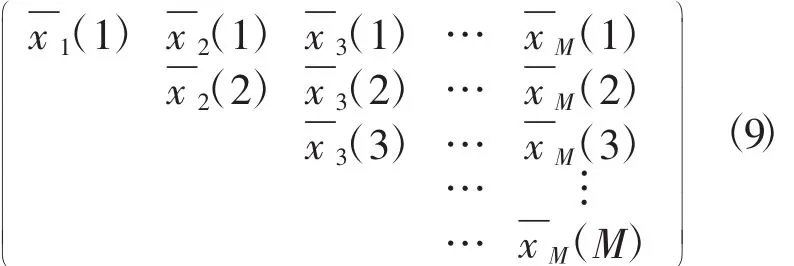
②提取优势周期目前有如下两种方法：

一是方差分析法。用下式检验x′（k）是否隐含长度为m的周期：

式中：F（m）为服从自由度为（m-1，n-m）的F分布

对于事先给定的置信水平α，若F（m）＞Fα（m-1，n-m），则认为x′（k）隐含长度为m的优势周期。

二是最大值法。欲确定长度为m的优势周期，只需取：

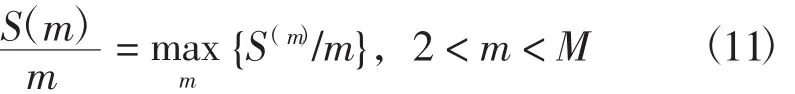
③由原始x′（k）序列减去周期m所对应的延拓均生函数构成一新序列，即x″=x′-fm（k），再对此新序列x″（k）重复步骤①②，可以进一步提取其它的优势周期。

④叠加。假设寻找到r个不同的优势周期，则令不同周期的同一时刻取值的迭加f（k）作为x′（k）的一个近似。

灰色—周期外延组合模型计算过程略微复杂，可使用Matlab编写程序实现。

2.3趋势外推法

趋势外推法是指通过建立自变量为时间，因变量为待推算指标序列的函数来推导得到历史数据的方法。趋势外推法前提假设是时间序列的态势具有稳定性或规律性，其主要依据时间序列的长期变化趋势得到历史数据。常用的非线性趋势外推模型有以下几种［2］：

二次多项式：

三次多项式：

指数函数：

修正指数曲线：

compertz曲线：

logistics曲线：

运用趋势外推法推算海洋经济历史数据的具体步骤如下：

①确定预选模型。根据数据序列折线图形状进行初步判断选定预选模型。

②估计预选模型的参数。二次多项式、三次多项式及指数模函数是可化为线性回归的模型，因此可采用最小二乘法进行参数估计；而修正指数曲线、compertz曲线、logistics曲线无法变换为线性回归，参数估计过程相对复杂，需要将三和法与非线性回归结合进行估计参数，即将三和法的计算结果作为非线性回归的初选值进行参数估计。

③计算推算值及可决系数。利用参数估计的结果计算得到各预选方法的推算值。然后，利用推算值及真实值计算可决系数，为后期进行模型选择提供依据。

④选定趋势外推模型。综合考虑模型拟合优度及推算结果合理性选定趋势外推模型：首先观察历史数据推算值的合理性；然后在推算值合理的趋势外推模型中选择拟合优度最高（即可决系数最大）的趋势外推模型作为最终使用的趋势外推模型。

二次多项式、三次多项式及指数模函数参数估计相对简单，运用Excel便可以实现。而修正指数曲线、compertz曲线、logistics曲线参数估计过程相对复杂，涉及非线性回归，可采用Matlab编写程序进行实现。

2.4指数平滑法

指数平滑法是在移动平均法基础上发展起来的一种时间序列分析预测法，它是通过计算指数平滑值，配合一定的时间序列预测模型对现象的未来进行预测。其原理是任一期的指数平滑值都是本期实际观察值与前一期指数平滑值的加权平均。常用的无季节变差的指数平滑方法有以下几种：

一次指数平滑：

式中：0≤α≤1为平滑因子。

二次指数平滑：

式中：Dt是双指数平滑序列。

Holt-Winters-无季节趋势：

式中：a表示截距，b表示趋势，

运用趋势外推法推算海洋经济历史数据与运用趋势外推法的步骤相似。具体步骤如下：

①确定指数平滑法的参数。指数平滑法的参数可以人为确定，也可以通过迭代计算得到。

②计算推算值及可决系数。利用确定的参数及上述公式，计算得到各指数平滑模型的推算值。然后计算各模型的可决系数为后期模型选择提供依据。

③选定指数平滑模型。综合考虑模型拟合优度及推算结果合理性选定指数平滑模型：首先观察历史数据推算值的合理性；然后在推算值合理的指数平滑模型中选择拟合优度最高（即可决系数最大）的指数平滑模型作为最终使用的指数平滑模型。

指数平滑法可通过Eviews直接实现。

3　各种方法的适用条件

不同数据条件适用不同的推算方法，在具体应用时需要根据实际情况选择适当的方法。当海洋经济相关指标缺乏历史数据而国民经济相应指标有历史数据，且海洋经济相关指标占国民经济相应指标的比重相对稳定或可用模型很好拟合时，可选用比重法；当比重法不适用，指标序列呈波动上涨或波动下跌趋势时可考虑选用灰色—周期外延组合模型；当比重法不适用，且指标序列曲线比较光滑时可考虑选用趋势外推法；当以上各种方法均不适用时，可考虑选用指数平滑法。此外，可根据具体情况选用多种方法组合使用。历史数据推算的主要流程如图1所示。

图1　历史数据推算流程图Fig.1Flow chart for deduction of historical data

4　实证分析

4.1比重推算法实证分析——以海水产品加工产量为例

《中国渔业统计年鉴》中海水加工产品产量仅有2003—2013年数据，但水产加工品总量有1989—2013年数据，且2003—2006年海水加工产品产量占水产品加工总量的比重相对稳定，在90%～93%之间，如表1所示。因此，采用1998—2002年水产品加工总量与2003—2006年海水加工产品产量占水产品加工总量的比重平均值的乘积作为海水加工产品产量的推算值，推算结果如表1所示。

表1　海水加工产品产量推算结果Tab.1Deduced results of output of processedmarine aquatic products

4.2灰色—周期外延组合模型推算法——以受污染海域面积为例

《中国海洋环境状况公报》中受污染海域面积（符合三类、四类及劣于四类海水水质标准的海域面积）只有2000—2013年数据，由于没有相应的国民经济指标，所以比重法不适用，而且由图2可知，指标序列整体呈现明显的波动变化特征。因此考虑采用灰色—周期外延组合模型推算历史数据，数据拟合情况如图2所示，拟合效果相对较好。

图2　受污染海域面积推算结果Fig.2Deduced results of polluted oceanic area

4.3趋势外推推算法——以主要沿海城市入境旅游人数为例

《中国海洋统计年报》和《中国海洋统计年鉴》中主要沿海城市入境旅游人数有1990—2013年数据。由于国民经济相关指标没有数据，且由图3可知曲线变化相对平滑，因此采用趋势外推法推算历史数据。观察曲线形状，初步判断可用指数、二次函数、三次函数模型推算历史数据。推算结果如图3所示。由图3可知指数模型拟可决系数最大，拟合优度最高且结果相对合理。可采用指数模型进行主要沿海城市入境旅游人数历史数据推算。

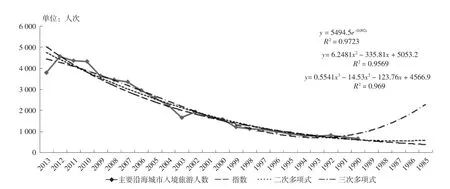
图3　主要沿海城市入境旅游人数推算结果Fig.3Deduced results of the number of inbound tourists received by major coastal cities

4.4指数平滑推算法——以沿海地区海洋造船完工量为例

《中国海洋统计年报》和《中国海洋统计年鉴》中沿海地区海洋造船完工量只有1995—2013年数据，而且没有单位相同、数据序列更长的相关指标，比重法不适用。由图4可知数据序列没有明显的波动特征，所以首先考虑使用趋势外推法，但是经计算，趋势外推法拟合效果不佳或推算结果不合理，所以考虑运用指数平滑法。由于2008年金融危机对海洋造船业影响较为明显，因此采用2008年以前数据运用指数平滑法推算历史数据。推算结果如下图所示，由图4可知，Holt-Winters无季节趋势指数平滑和二次指数平滑拟合效果优于一次指数平滑。为进一步比较分析Holt-Winters无季节趋势指数平滑和二次指数平滑的拟合优度，计算两者的可决系数。Holt-Winters无季节趋势指数平滑可决系数为0.941，二次指数平滑可决系数为0.936。因此，Holt-Winters无季节趋势指数平滑拟合效果较好，可采用Holt-Winters无季节趋势指数平滑推算沿海地区海洋造船完工量历史数据。

图4　沿海地区海洋造船完工量推算结果Fig.4Deduced results of marine shipbuilding completions by coastal regions

5　结语

本文系统详细阐述了比重法、灰色—周期外延组合模型、趋势外推法、指数平滑法在进行海洋经济历史数据推算的具体步骤，以及各种方法的适用条件，并应用上述方法对几个海洋经济指标进行了实证分析。实证结果显示，根据指标数据实际情况选用适当方法能够较好推算海洋经济历史数据，一定程度上缓解海洋经济历史数据序列较短的问题，以满足各种模型方法的数据需要。但是，本文所述海洋经济历史数据推算方法只适用于个别指标缺少少量数据的情景。对于大量指标缺少历史数据或个别指标缺少大量历史数据的海洋经济研究，建议不要使用历史数据推算的方法延长数据序列。

此外，在海洋经济历史数据推算的过程中，可根据情况采用多种方法组合的形式进行历史数据推算。如沿海城市国内旅游人数，沿海城市国内旅游人数有2002—2013年的数据，而全国国内旅游人数有1997—2013年的数据，但是由于沿海城市国内旅游人数占全国国内旅游人数的比重并不稳定，所以推算1997—2001年沿海城市国内旅游人数时，需要首先推算1997—2001年沿海城市国内旅游人数占全国国内旅游人数比重。因此，进行沿海城市国内旅游人数历史数据推算时可将趋势外推法与比重法组合使用：首先使用趋势外推法推算比重，然后运用比重法推算其历史数据。

［1］赵昕，宋维玲，何广顺.海洋灾害直接经济损失预测——基于灰色一周期外延组合模型［J］.海洋开发与管理，2007（6）：100-106.

［2］易丹辉.数据分析与EVIEWS应用［M］.中国统计出版社，2002.

Research on the Deduction Methods of Marine Economic Historical Data

Li Linlin，Song Weiling，Zheng Li，Lin Xianghong，Cai Dahao
（National Marine Data and Information Service，Tianjin 300171，China）

Marine economy is increasingly attracting attention from all circles of society，so are the marine economic statistic data.However，the development of marine statistics needs long-termeffort.In order to meet the needs of economic analysis，it is necessary to deduce the historical data of marine economy to extend the marine economic data series.Based on research and practice，this paper summarized some methods that can be applied to the deduction of marine economic historical data，such as proportionmethod，gray-periodic extensional combinatorial model，trend extrapolation，exponential smoothing etc.Also we illustrated the applicable conditions of every method and employed empirical analysis to testify those methods.The exemplified result shows that marine economic historical data can be deduced at a relatively acceptable accuracy，if we selectappropriatemethod according to the data situation.But the methods can be appliedonlywhen a small amount of dataare lacked.And multiple methods can be combined to deduce the historical data if it is necessary.

marineeconomy；marinestatistics；deductionmethod

F222.3

A

2095-1647（2015）05-0041-07

2015-07-03

李琳琳，女，硕士，主要研究方向为：海洋经济计量分析，E-mail：lilinlin.1988@liyun.com。