基于人因仿真分析的装配序列评价模型及应用

马红占　褚学宁　刘振华　李玉鹏

上海交通大学，上海， 200240

基于人因仿真分析的装配序列评价模型及应用

马红占褚学宁刘振华李玉鹏

上海交通大学，上海， 200240

为减少装配作业疲劳，降低动作强度，提高装配质量和效率，提出了一种基于人因工程仿真分析的装配序列综合评价模型。以装配序列的人因性能优劣为目标，创建了包含定量与定性指标在内的综合评价指标体系；提出了装配序列人因工程仿真分析模型，通过虚拟仿真技术与人因分析方法获取人因性能的基础指标属性值。采用客观自适应熵权法和改进模糊层次分析法分别确定各定量指标和定性指标的权重，利用三角模糊数定量化定性评价值，基于Topsis框架得到适合人体作业的最优装配序列。最后结合Tecnomatix数字化仿真平台将该评价模型应用于某航天产品减速器可行装配序列的优选，验证了方法的有效性。

装配序列评价；人因仿真分析；熵权法；模糊层次分析

0　引言

装配序列是对装配体按照一定的约束规则规划出的装配顺序，是装配序列规划领域内的重要内容[1]。装配序列不同，装配效率、质量和成本也不同，如何在有限的可行装配序列中快速准确地选取满足装配工艺约束条件和人体装配作业需求的最优装配序列，关键在于能否对候选装配序列作出综合全面的评价。

现有装配序列评价的相关研究中，大部分学者从装配序列成本最小化、装配效率最大化角度进行装配序列评价，认为实现产品装配的关键在于满足装配工艺性(如装配并行性等)的要求。如：Eftekharian等[2]分析了复杂装配体的几何模型，结合经验知识与几何推理技术对装配序列的操作时间进行了评估；Zhang等[3]基于装配序列的并行性，采用“最优序列参考集”进行装配性能隶属度的计算，根据实际装配需求建立评价指标体系，并采用层次分析法进行装配序列评价；张嘉易等[4]根据装配工艺的具体性要求提出了单元性与整体性评价指标相结合的装配综合评价方法；李磊等[5]分析了影响装配序列品质的12个因素，提出二级模糊综合评价模型评价各候选序列。但是这些装配评价模型在评价指标上过于关注序列本身，忽略了装配序列与作业人员之间的相互影响；另外，以往评价模型在设计阶段获取序列评价数据时主要依赖于CAD系统的设计数据，缺乏对工人装配过程的参考，事实上也很难深入了解工人的实际装配需求。但是随着装配作业的标准化程度不断提高和装配分工的细化，越来越多的劳动者因装配作业姿态、装配时间、装配距离、装配视野域等不合理引起了人体过早疲劳和累积损伤，导致职业病频繁发生[6]。因此，在重视装配成本和效率的同时，还应更多关注装配工艺是否符合人体的作业需求[7]。对装配序列进行人因仿真分析的研究，进一步改善了装配序列评价方法，对提高整个生产系统的绩效具有非常重要的意义。

为减少作业疲劳，降低动作强度，提高装配质量和效率以获得适合人体作业的最优装配序列，本文基于人因工程学的原理从人体装配需求角度出发，建立了定性和定量相结合的装配序列人因性能综合评价指标体系；提出了人因仿真分析模型，在装配仿真的基础上进行了数据获取；最后应用熵权法、模糊层次分析法、三角模糊数与Topsis算法得出人因性能最优的装配序列。

1　装配序列人因性能评价模型

将装配序列人因性能定义为装配序列满足装配工艺约束条件和人体装配需求的程度，假设在装配工艺设计初期，通过装配序列规划与设计得到了若干可行的装配序列，现在需要根据装配工艺约束条件和人体装配需求，确定人因性能最优的装配序列。为解决这一问题，首先建立装配序列人因性能评价指标体系，包括定量指标(装配可达性指标)与定性指标(可视性指标与舒适性指标)；然后，借助人因仿真分析模型获取人因相关评价数据(比如装配距离、装配视角优劣等)，从CAD三维模型系统中提取与装配工艺约束相关的属性值(比如配合间隙、接触类型等)；之后，为保证定量指标评价的客观性与应对定性指标评价的模糊性，在确定指标权重和方案评价值时，采用熵权法与模糊层次分析法分别确定定量指标与定性指标的权重，采用规范化矩阵获得装配序列在定量指标下的评价值，定性指标评价值的确定则利用三角模糊数表示；最后，采用Topsis算法进行候选装配序列的排序优选。装配序列人因性能评价的框架如图1所示。

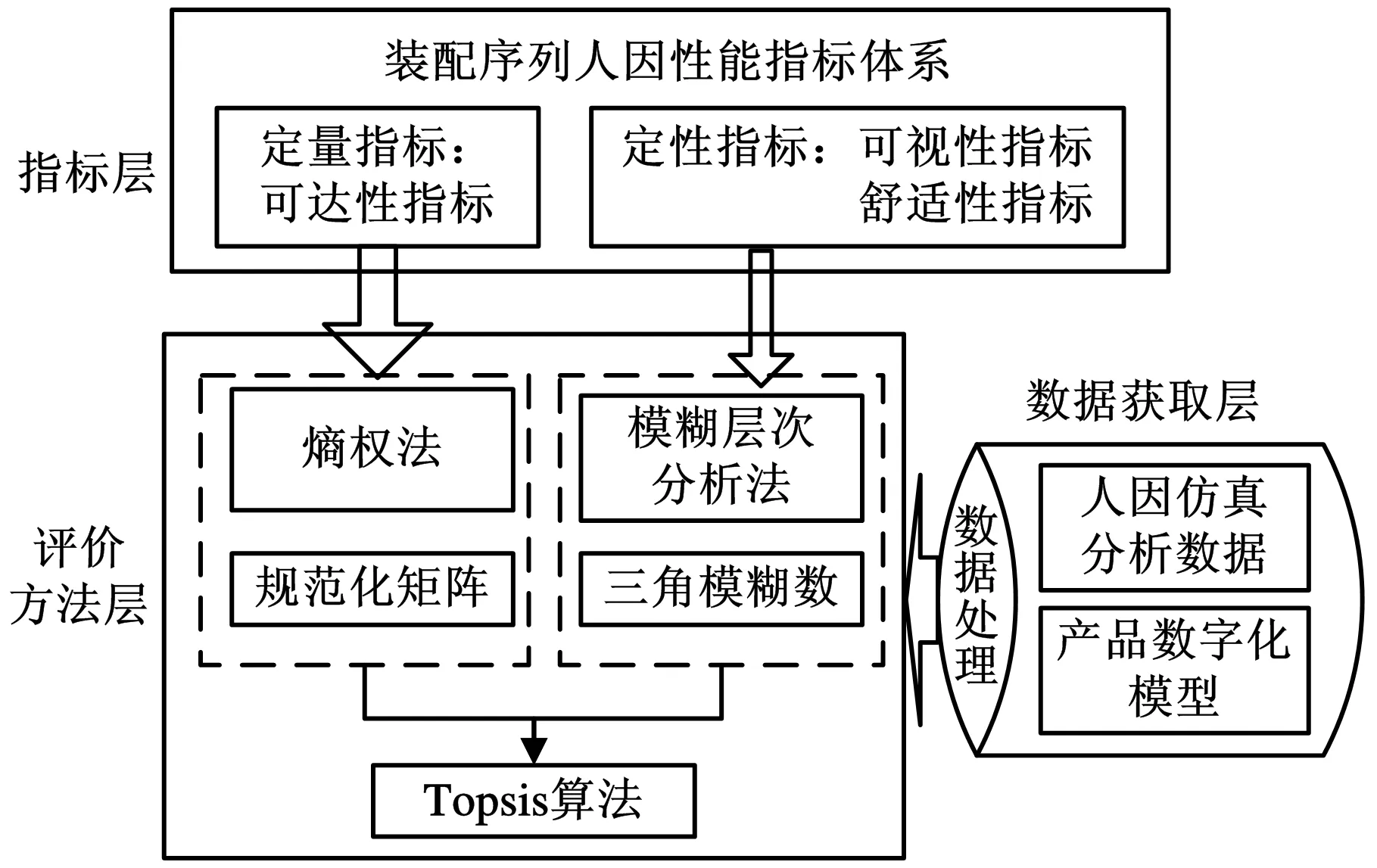
图1　装配序列人因性能评价模型总体架构

2　装配序列评价指标体系

装配序列评价涉及的评价指标众多，既有定性指标，也有定量指标。从现场装配工人的装配需求角度出发，将影响产品装配序列质量的因素分为装配可达性、装配可视性、装配舒适性指标三大指标，构建如图2所示的装配序列评价指标体系。

3　装配序列人因仿真分析与数据获取

本文在虚拟系统中对装配操作人员进行作业仿真，采用人机交互的方式获取装配序列人因性能评价所需的相关数据。在总结人因工程仿真分析相关研究的基础上[6-7]，提出装配序列人因工程仿真分析的模型如图3所示，包含装配数据信息层、仿真层和数据记录与分析层。

将装配数据信息层与仿真层的输出作为仿真数据记录与分析层的输入，记录与分析层的结果是确定人因性能指标属性值的数据来源。从仿真系统中获取装配序列人因性能评价的来源与传统装配序列评价的数据来源相比具有如表1所示的优点。

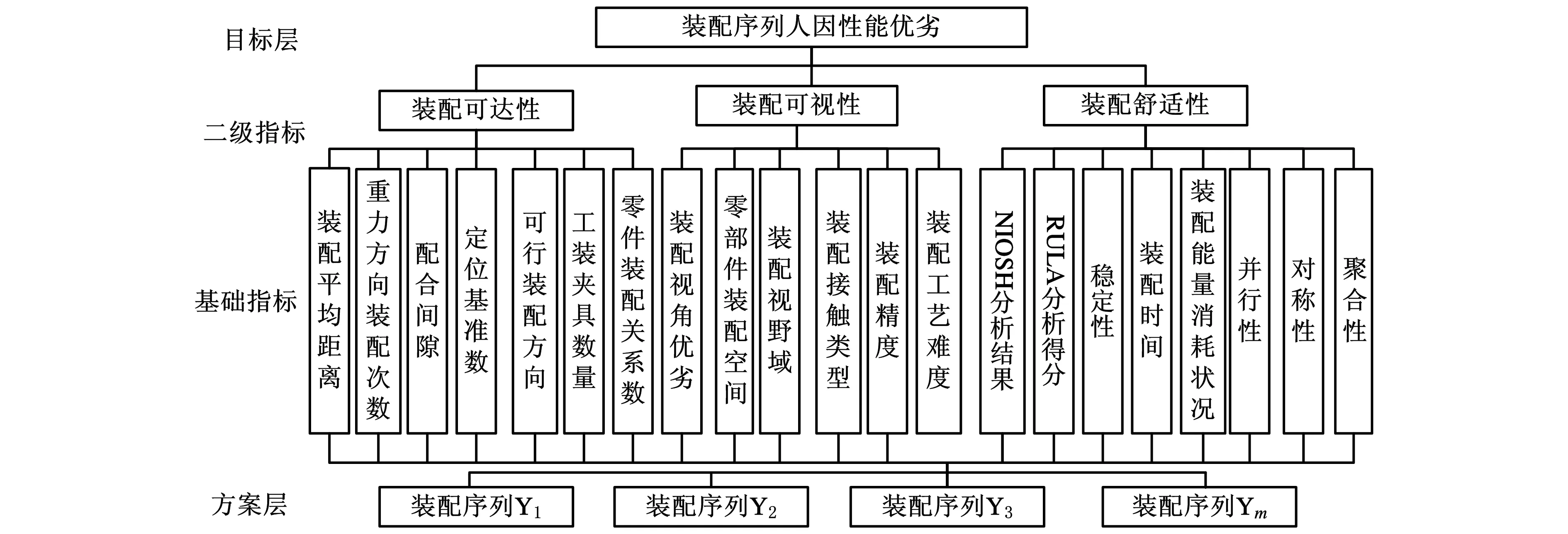
图2　装配序列人因性能评价指标体系

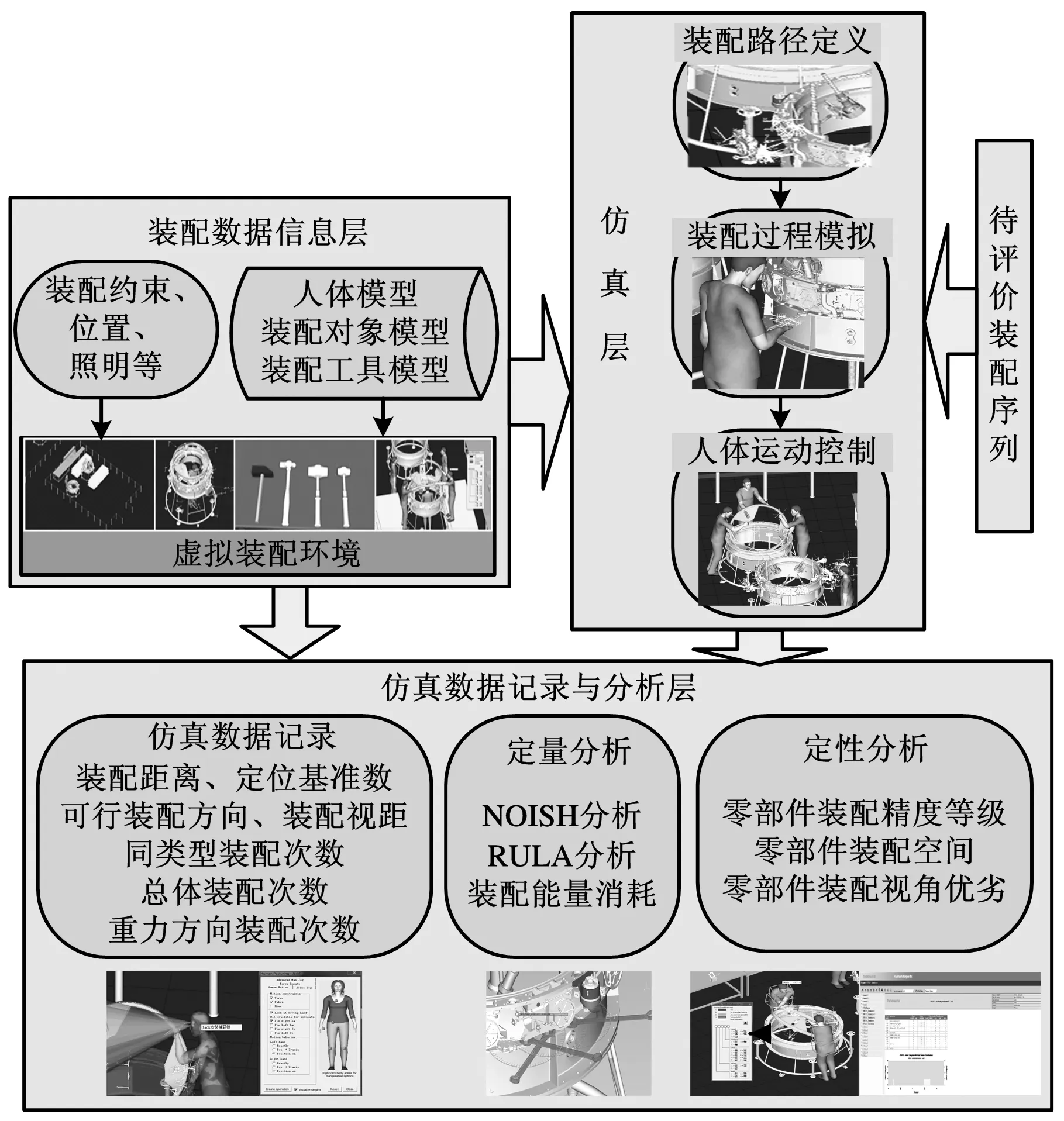
图3　装配序列人因仿真分析模型

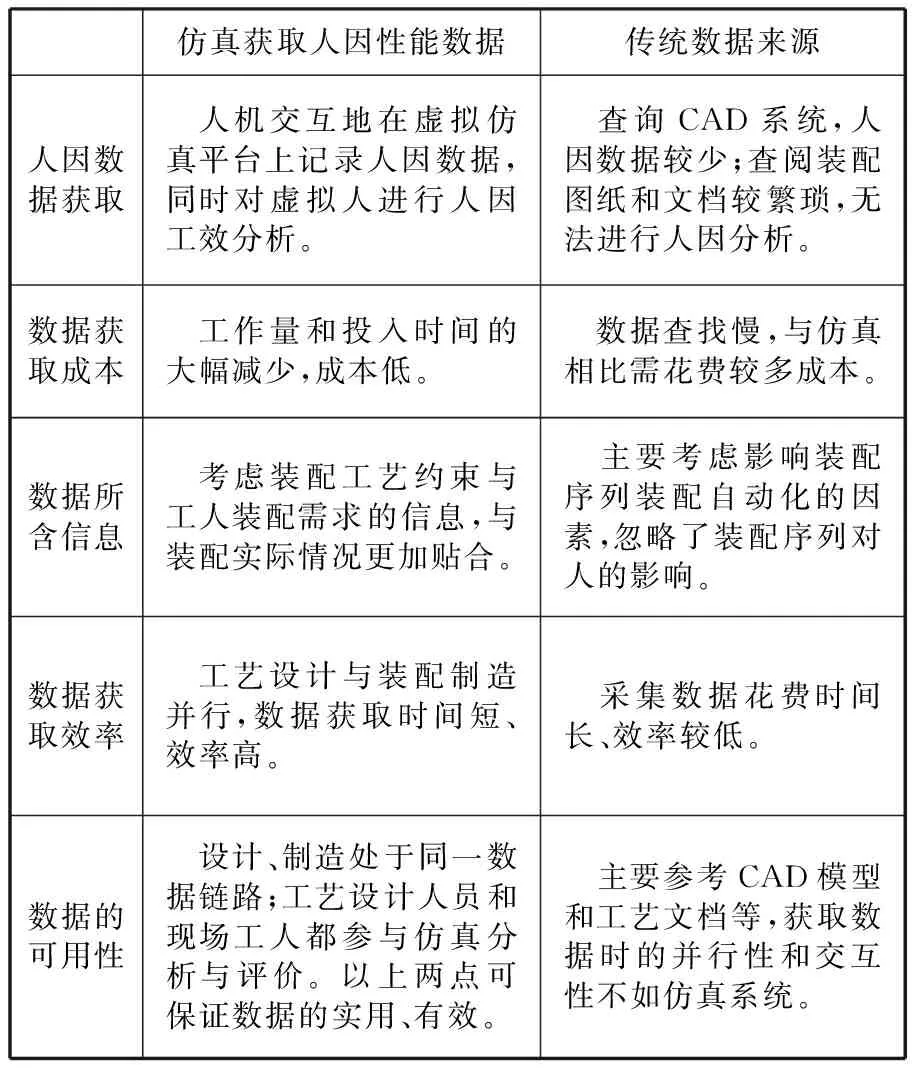
仿真获取人因性能数据传统数据来源人因数据获取 人机交互地在虚拟仿真平台上记录人因数据,同时对虚拟人进行人因工效分析。 查询CAD系统,人因数据较少;查阅装配图纸和文档较繁琐,无法进行人因分析。数据获取成本 工作量和投入时间的大幅减少,成本低。 数据查找慢,与仿真相比需花费较多成本。数据所含信息 考虑装配工艺约束与工人装配需求的信息,与装配实际情况更加贴合。 主要考虑影响装配序列装配自动化的因素,忽略了装配序列对人的影响。数据获取效率 工艺设计与装配制造并行,数据获取时间短、效率高。 采集数据花费时间长、效率较低。数据的可用性 设计、制造处于同一数据链路;工艺设计人员和现场工人都参与仿真分析与评价。以上两点可保证数据的实用、有效。 主要参考CAD模型和工艺文档等,获取数据时的并行性和交互性不如仿真系统。

4　评价流程

设有m个候选装配序列，n个评价指标，各候选装配序列的评价指标值组成评价矩阵R，rij表示第i个候选装配序列的第j个评价指标值。为保证序列定量指标值的客观性与解决定性指标值的不确定性，分别运用信息熵和模糊层次分析法确定其权重。

4.1定量指标权重确定

信息熵在确定候选方案的评价指标权重方面具有较好的客观性[8]。由于定量具有不同的量纲，无法直接比较，因此必须对指标值矩阵进行规范化。装配序列指标类型主要分为效益型和成本型两种。效益型要求参数值越大越好，成本型要求参数值越小越好。结合装配序列定量化指标，给出定量化指标规范化计算公式如下。

(1)效益型指标规范化:

(1)

j=1,2,…,n

式中，xij为第i个序列的第j项指标的评价值。

(2)成本型指标规范化：

(2)

利用熵权法来确定各装配序列整体评价指标的客观权重wj，步骤如下。

(1)计算第i个装配序列第j项定量指标的评价值比重pij：

(3)

(2)计算第j项指标的熵Ej：

(4)

(3)计算第j项指标的偏差度Gj：

Gj=1-Ej

(5)

(4)计算第j项定量指标的权重wj:

(6)

4.2定性指标的量化与权重确定

为了客观合理地反应定性因素对装配序列人因性能的影响，采用三角模糊数表示定性指标评价值与装配人因性能优良的匹配程度。在每一项定性指标下，采用五粒度语言评价短语{极优(VG)，优(G)，中等(M)，差(P)，极差(VP)}对装配序列的人因指标给出评价，按照评价短语转化表进行量化[9]，得到候选序列在每一定性指标下的三角模糊值xij=(aij,bij,cij)，其中，aij为模糊数的上界，cij为模糊数的下界，bij为模糊数最有可能取得的值。进而得到模糊评价矩阵X=[xij]m×n。

模糊层次分析法(FAHP)在指标模糊评判中应用广泛，可以处理决策过程中的不确定性[10]，由于传统的FAHP方法获得的三角模糊权重不是所需的指标因素权重信息的完全确知状态，故本文采用改进的FAHP方法对三角模糊权重进行处理，具体计算步骤如下：

(1)由工艺设计专家运用比较语气算子进行指标的两两比较，采用三角模糊数得出定性指标的评判矩阵，其中，下三角数值通过对上三角数值取反获得。

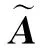
(7)

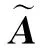
(4)由式(8)求得第i个因素相对于上一层因素的三角模糊数权重:

(8)

(9)

(5)设上层指标包含U个因素，U层因素的总排序权重设为u1，u2，…，uU,对应的下层指标包含L个因素，其相对于U层的某一指标Uf的单因素权重为l1i，l2i，…，lLi。L层各因素相对于目标层的权重可由下式计算得到：

(10)

e=1,2,…,Lf=1,2,…,U

4.3基于Topsis框架的装配序列综合评价

Topsis算法是一种广泛应用的多属性评价方法，它通过计算各评价方案与理想值的欧氏距离得出相对接近度，然后将相对接近度进行排序获得最优方案[11]，具体步骤如下。

(1)评价指标值的定量化。对于定量指标，可由式(1)与式(2)规范化得到；定性指标所对应的量化值可由下式反模糊化得到：

(11)

(2)构建加权综合评价矩阵：

Z=[zij]m×n=[wjrij]m×n

(3)计算装配序列候选方案的正理想值Z+与负理想值Z-:

对于成本型指标，正理想值中的元素取候选方案中的最小值，负理想值中的元素取取候选方案中的最大值。

(4)确定各候选装配序列方案与正负理想值的欧氏距离:

(12)

(13)

(5)根据下式计算各候选装配序列指标值向量与理想向量之间的相对接近度：

(14)

5　实例应用

将装配序列人因性能评价模型应用到图4所示的某航天产品减速器的装配序列评价中，以验证其有效性。简化标准件和紧固件之后，该部件由19个刚性部件组成(图4)。

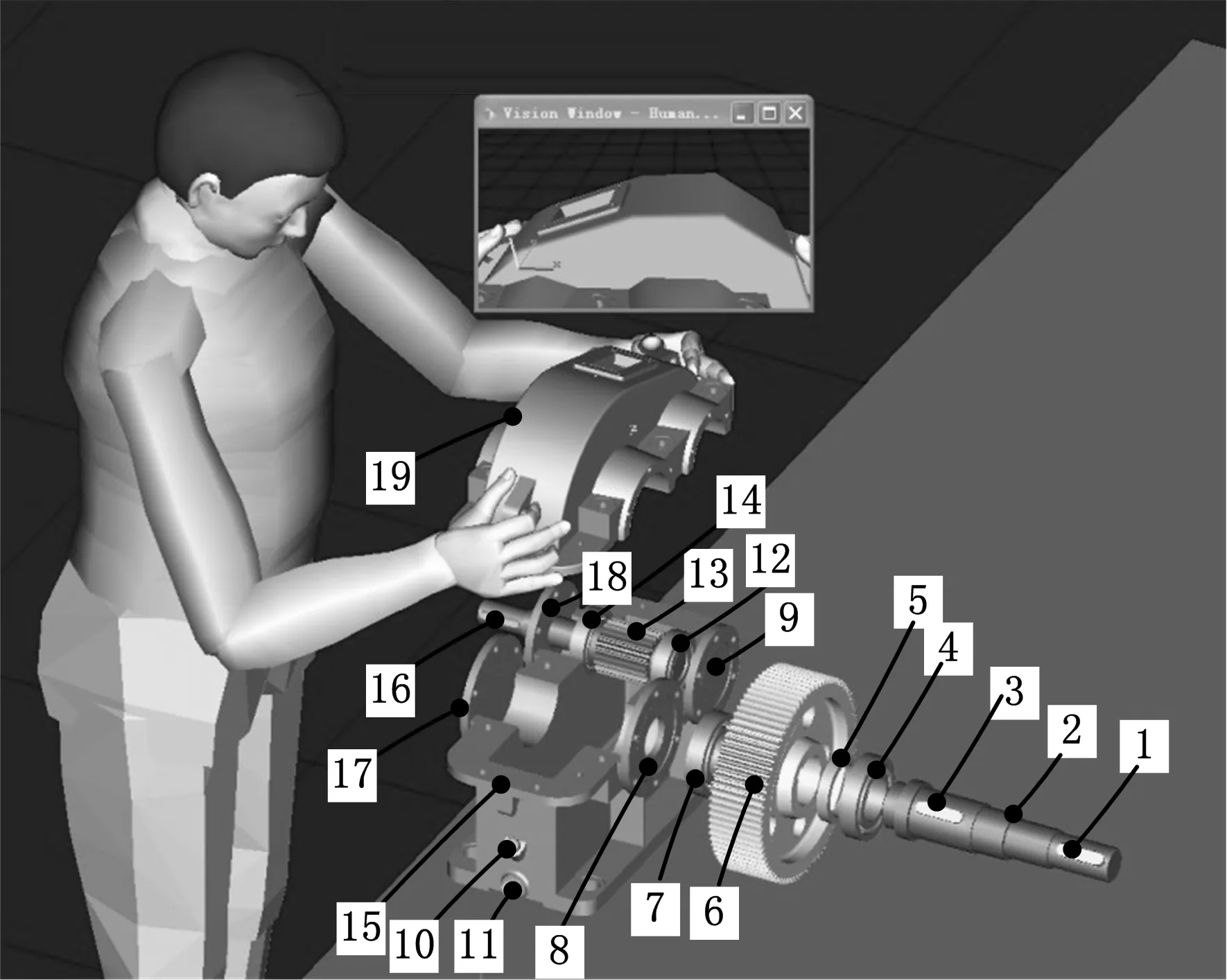
图4　人因装配仿真爆炸图

参考人因仿真分析模型对图5所示的3条可行装配序列进行装配路径的定义和人因工程仿真，结合建模时的工程信息读取并记录装配可达性指标下的定量指标属性值，如图4所示，以零件19的装配距离值获取为例，通过记录其初始装配位置和目标位置，可以计算出其装配距离。最后统计分析所得到的基础数据如表2所示。

(a)可行装配序列A1

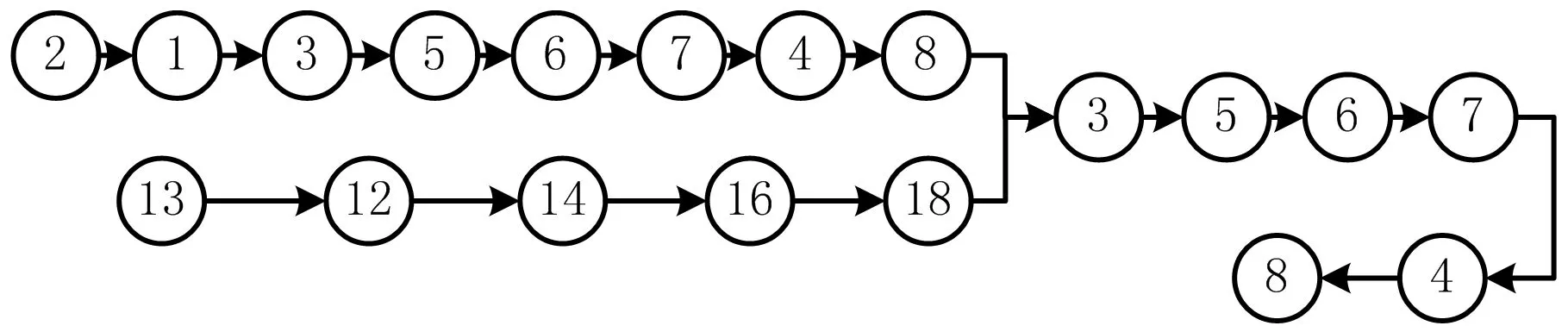
(b)可行装配序列A2

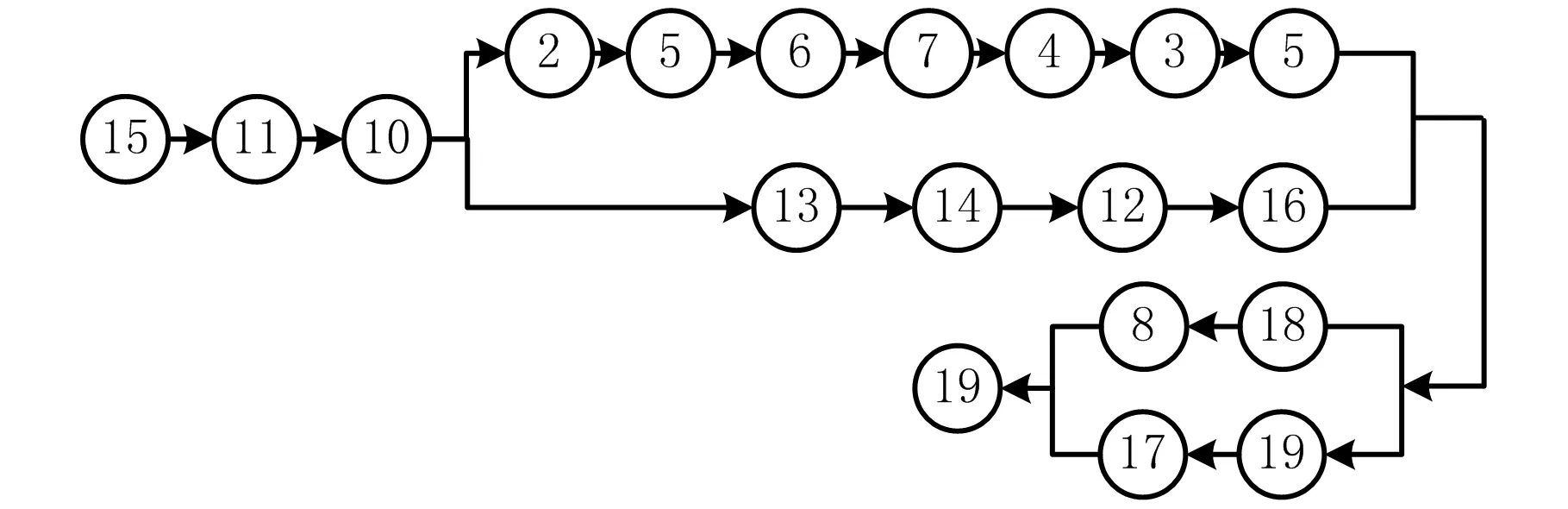
(c)可行装配序列A3图5　可行装配序列

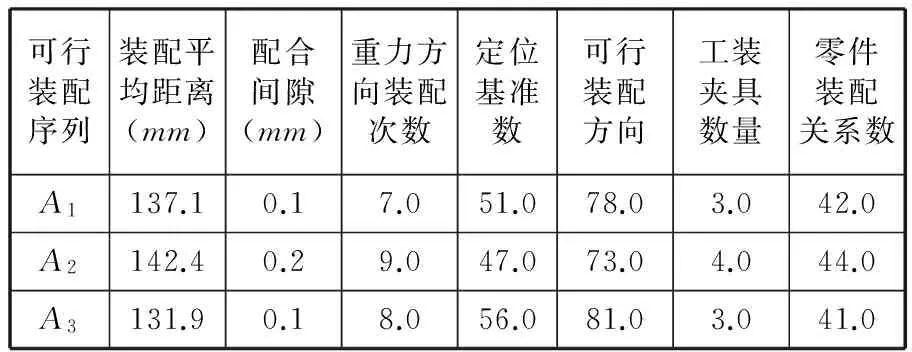
可行装配序列装配平均距离(mm)配合间隙(mm)重力方向装配次数定位基准数可行装配方向工装夹具数量零件装配关系数A1137.10.17.051.078.03.042.0A2142.40.29.047.073.04.044.0A3131.90.18.056.081.03.041.0

从设计部门、工艺处和装配车间抽调三名工程师组成评价专家组，采用人机交互方式对Tecnomatix虚拟仿真系统中的每条装配序列进行可视性和舒适性指标的评价。限于篇幅，本文以上端盖19的人因装配仿真为例，在Tecnomatix虚拟平台中开启人眼的视野域窗口，专家组根据仿真结果给出相应评价结果。同样结合NIOSH和RULA分析理论，对仿真结果进行舒适性指标的评价。统计得到的评价结果如表3所示。

表3　装配序列的可视性与舒适指标属性值

确定定性指标权重时，统一取决策因子λ=0.5。考虑到航天产品本身作业空间和装配精度等方面的要求，对装配的可视性有所偏重，从人员作业舒适安全的角度考虑，对装配人员作业的舒适性有所偏重。经计算得到各级指标的权重如表4所示。

表4　各级评价指标权重值

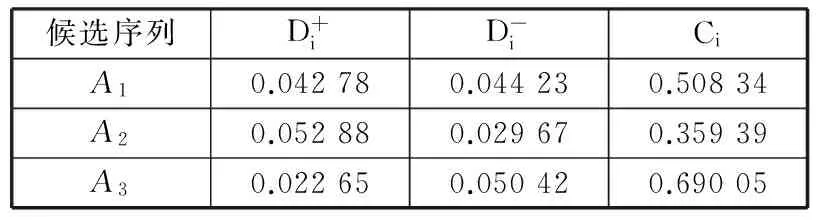
表5　装配序列人因性能优劣排序

根据各方案与理想解的相对接近程度从大到小进行排序，则装配序列的人因性能的优劣顺序为A3≻A1≻A2。

应用实例说明本文所提装配序列评价模型能够根据装配序列的工人需求和装配工艺约束指标的要求，对几何可行的装配序列进行人因性能评价，实现了在多个可行装配序列中选取最优装配序列的目的。

6　结论

(1)基于人因工程学的原理，从人体装配需求角度出发，建立了定性和定量相结合的装配序列人因性能综合评价指标体系。

(2)提出了装配序列人因工程仿真分析模型，在装配仿真基础上进行评价数据获取。

(3)应用熵权法、模糊层次分析法、三角模糊数与Topsis算法得出了人因性能最优的装配序列。

(4)结合装配仿真系统中进行应用，满足了装配工艺约束条件和人体装配作业需求，实现了对人工参与的几何可行装配序列的优选，保证了数字化装配人因工程仿真与装配序列规划技术的工程有效性，对于降低装配人员疲劳度、保证作业安全和合理规划装配工艺具有重要的现实意义。

[1]KanaiS,TakahashiH,MakinoH.Computer-aidedAssemblySequencePlanningandEvaluationSystemBasedonPredeterminedTimeStandard[J].CIRPAnnals-ManufacturingTechnology, 1996, 45(1): 35-39.

[2]EftekharianAA,PoladiR,CampbellMI.EvaluationandSearchofAssemblySequencesinLargeSystems[C]//ASME2013InternationalDesignEngineeringTechnicalConferencesandComputersandInformationinEngineeringConference.Portland,OR,Unitedstates, 2013:V02AT02A041.

[3]ZhangJY,ZhaoLN,HaoYP,etal.EvaluationonParallelAssemblySequence[J].AdvancedMaterialsResearch, 2013, 734: 2757-2760.

[4]张嘉易, 王成恩, 马明旭, 等. 产品装配序列评价方法建模[J]. 机械工程学报, 2009, 45(11): 218-224.

ZhangJiayi,WangCheng’en,MaMingxu,etal.ModelingoftheMethodofProductAssemblySequenceEvaluation[J].JournalofMechanicalEngineering, 2009, 45(11): 218-224.

[5]李磊, 魏生民, 张军波. 装配序列的模糊综合评价[J]. 中国机械工程, 2003, 14(18): 1606-1609.

LiLei,WeiShengmin,ZhangJunbo.FuzzyComprehensiveEvaluationofAssemblySequence[J].ChinaMechanicalEngineering, 2003, 14(18): 1606-1609.

[6]HusainA,KhanAA,HasanF.ErgonomicEvaluationofEffectsofHandleShapeandTaskOrientationonHumanPerformanceinScrewDrivingTask[J].InternationalJournalofAdvancementsinTechnology, 2013, 4(1): 105-114.

[7]张晓冬,杨育,易树平,等. 制造系统人因仿真参考模型及若干关键技术[J]. 机械工程学报,2006,42(3):56-63.

ZhangXiaodong,YangYu,YiShuping,etal.ReferenceModelandKeyTechnologyforHumanFactorsSimulationManufacturingSystem[J].JournalofMechanicalEngineering,2006,42(3):56-63.

[8]Rao,G,FengF,SiA,etal.MethodforOptimalDeterminationofParametersinPermutationEntropyAlgorithm[J].JournalofVibrationandShock, 2014,33(1):188-193.

[9]Nieto-MoroteA,Ruz-VilaF.AFuzzyApproachtoConstructionProjectRiskAssessment[J].InternationalJournalofProjectManagement, 2011, 29(2): 220-231.

[10]RuoningX,XiaoyanZ.FuzzyLogarithmicLeastSquaresRankingMethodinAnalyticHierarchyProcess[J].FuzzySetsandSystems, 1996, 77(2): 175-190.

[11]KrohlingRA,CampanharoVC.FuzzyTOPSISforGroupDecisionMaking:aCaseStudyforAccidentswithOilSpillintheSea[J].ExpertSystemswithApplications, 2011, 38(4): 4190-4197.

(编辑王艳丽)

Assembly Sequences Evaluation Modeling and Application Based on Human Factor Simulation Analysis

Ma HongzhanChu XueningLiu ZhenhuaLi Yupeng

Shanghai Jiaotong University,Shanghai,200240

In order to reduce the assembly work fatigue, reduce the intensity of action and improve the assembly quality and efficiency, a comprehensive evaluation model was proposed to evaluate feasible assembly sequences objectively based on human factor simulation analysis. Taking human factor performance of assembly sequences as the goal, a comprehensive evaluation index system including quantitative and qualitative indicators was created as well as human factor engineering simulation analysis model for assembly sequences was proposed, on the basis of it, the attribute value of basic index could be obtained by virtual simulation technology and human factor analysis method.The weights of quantitative index and qualitative index were determined by adopting objective and adaptive entropy method and fuzzy analytic hierarchical process respectively, qualitative evaluation value was quantified using triangular fuzzy number, then based on Topsis framework, the optimal assembly sequence can be drawn. Finally, the evaluation model was applied to a aerospace product reducer feasible assembly sequence optimization combined with Tecnomatix digital simulation platform, verifying its validity.

assembly sequence evaluation; human factor simulation analysis; entropy method; fuzzy analytic hierarchy process

2014-01-02

上海市科技创新行动计划资助项目(11dz1120800，12dz1125600)；国家自然科学基金资助项目(51475290，51075261)；高等学校博士学科点专项科研基金资助项目(20120073110096)

TP391.7< class="emphasis_italic">DOI

：10.3969/j.issn.1004-132X.2015.05.015

马红占，男，1991年生。上海交通大学机械与动力工程学院硕士研究生。主要研究方向为数字化制造。褚学宁(通信作者)，男，1961年生。上海交通大学机械与动力工程学院教授、博士研究生导师。刘振华，男，1985年生。上海交通大学机械与动力工程学院博士研究生。李玉鹏，男，1984年生。上海交通大学机械与动力工程学院博士研究生。