新型3-PRRS并联机构的位置正反解分析

郭宗和　杜晴晴　杨启志

1.山东理工大学,淄博,255049　　2.江苏大学,镇江,212013

新型3-PRRS并联机构的位置正反解分析

郭宗和1杜晴晴1杨启志2

1.山东理工大学,淄博,2550492.江苏大学,镇江,212013

对新型六自由度3-PRRS并联机构进行运动学分析,推导了解析形式的运动学反解,利用封闭解法研究其运动学全部正解。根据每条支链2个转动副对动平台的不同影响，通过坐标变换和引入角度变量φi,得到动平台3个铰链点坐标;以这三点之间的固定长度为约束条件,建立约束方程，得到以φi为变量的3个超越方程,通过消元法得到16次线性代数方程;利用MATLAB软件编程求解全部位置正解。应用算例对位置正反解进行了数值验证,正解结果与反解结果吻合。研究结果为应用于虚拟轴并联机床的新型3-PRRS并联机构的尺度综合、奇异位形分析、输出误差分析和轨迹控制等方面的研究奠定了基础。

并联机构;封闭解法;位置正反解;六自由度

0　引言

一般来讲，并联机构支链较多会使得机构工作空间与机构体积比变小，灵活性变差，容易产生干涉,机构的奇异位形相对较多，并且运动学正解复杂,而少支链六自由度并联机器人以其结构紧凑、造价低及工作空间大等优点成为当前六自由度并联机构的研究热点[1-2]。目前,拥有3 个运动支链的六自由度并联机构(如3-PPSP、3-RRPS、3-PRPS 和3-URS等机构)的研究取得了一定的进展[1,3-6]。运动学正解是研究并联机构许多问题的根基[7],其解法主要有数值法和解析法。数值法的速度慢、效率低，并且不能求出所有可能的解，因此人们总希望采用解析法来求解并联机构的封闭解[8]。一些学者采用代数消元法、位姿解耦法、载波混沌Newton法求解了位置正解[9-12]。

文献[13]提出了一种基于PR驱动的六自由度3-PRRS并联机构,验证了机构的输入合理性，并用几何方法推导了运动学反解。六自由度3-PRRS并联机构具有运动稳定、提供纯转动、可直观预测动平台运动等特点，在虚拟轴并联机床领域有着广阔的应用前景。

本文利用封闭矢量法系统地分析了六自由度3-PRRS并联机构的运动学正反解求解问题。推导了解析形式的运动学反解；分析每条支链上2个转动副对动平台的影响，通过坐标变换和引入角度变量φi(i=1,2,3)，推导出动平台3个铰链点坐标，建立约束方程，得到只含有变量φi(i=1,2,3)的超越方程,利用消元法和MATLAB软件编程求解得到全部位置正解；通过给定的与处于设计阶段的六自由度并联机床结构参数相同的数据来进行数值验证，证明该方法确实简单有效。

1　机构位置

1.1机构描述与坐标系建立

图1　3-PRRS并联机构结构简图

图1为3-PRRS并联机构结构简图。该机构由静平台M1M2M3、动平台a1a2a3以及连接2个平台的3条均匀分布且结构相同的支链组成，每条支链均由1个移动副P以及转动副R1、转动副R2和一个球副S组成。其中,与移动副相连的转动副R1的轴线始终与静平台平行，与连杆L1、L2、L3相连的转动副R2的轴线与转动副R1轴线相互垂直。连杆L1、L2、L3的长度l1、l2、l3均为l,移动副P和转动副R1为驱动副。点A1、A2、A3分别为移动杆与静平台的交点，点a1、a2、a3分别为连杆L1、L2、L3与动平台连接的球副S的中心,动平台的直径为d，静平台(虚线部分，即转动副R2的中心点Ti在静平台上的投影，投影点为Mi)直径为D。分别在动平台、静平台的中心P、O点建立空间直角坐标系Pxyz、OXYZ,z、Z轴分别垂直于动平台、静平台，x、X轴分别指向点a1、A1,y、Y轴的确定符合右手定则,u1、u2、u3分别为相对应的支链上与转动副R2的转动轴线共线的向量。

图2为转动副输入转角为θi(i=1,2,3)时在Ti点建立的局部坐标系Tiuvw(i=1,2,3)示意图。其中,u轴与转动副R1的转动轴线共线并指向外,v轴与转动副R2的转动轴线共线并与ui方向一致,w轴符合右手定则,φi为连杆Li与局部坐标系Tiuvw中的w轴的夹角。

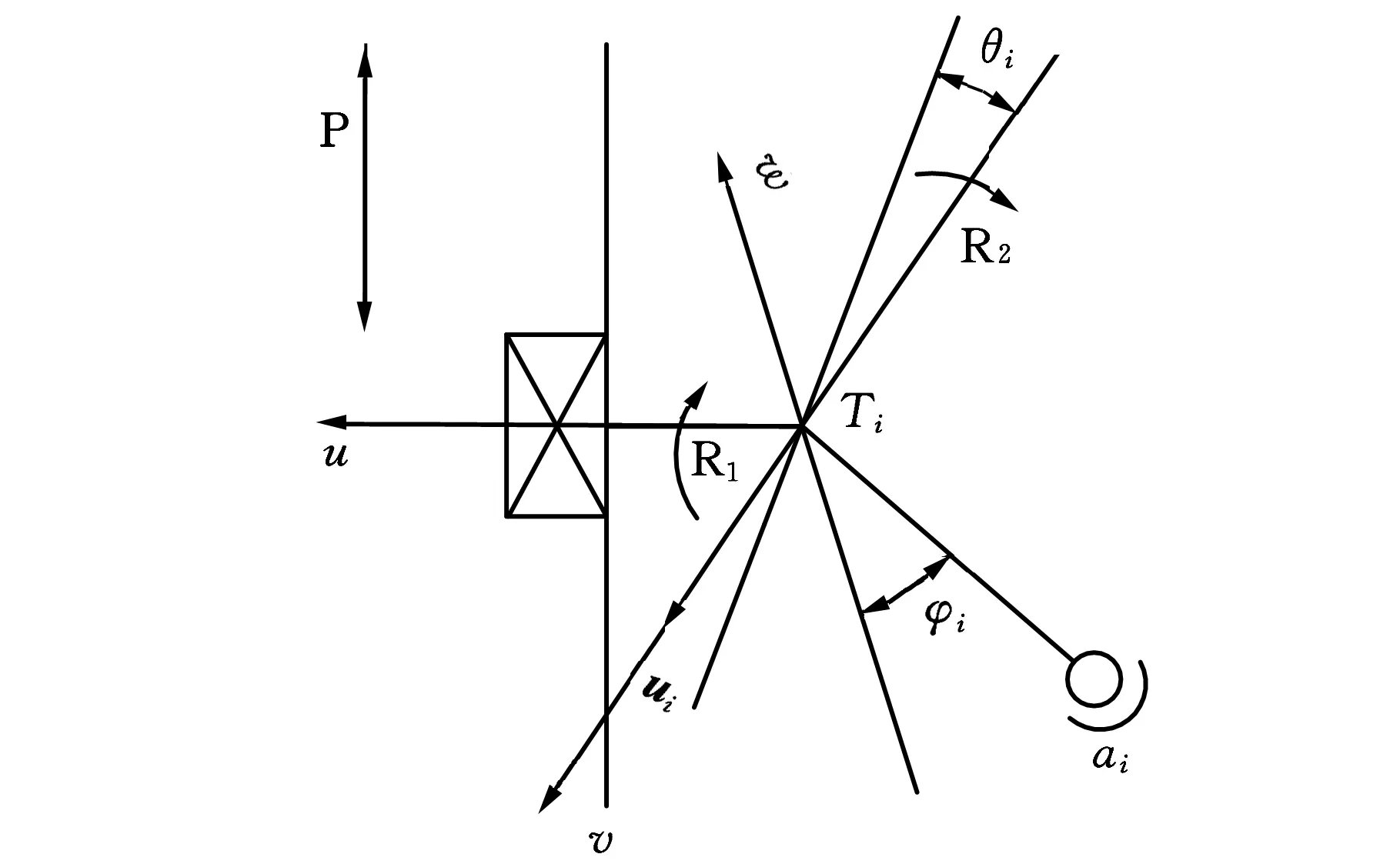
图2　转动副输入转角为θi时在点Ti建立的局部坐标系Tiuvw

1.2机构位置反解

六自由度3-PRRS并联机构位置反解问题可归结为如下问题:已知机构的尺寸参数和动平台中心点P的位姿(XP,YP,ZP,α,β,γ),求解机构各支链上移动副P的输入位移Si(i=1,2,3)和转动副R1的输入转角θi(i=1,2,3)。

根据上述定义的坐标系，动坐标系Pxyz相对于静坐标系OXYZ的旋转矩阵T按照Z→Y→X的变换顺序可得：

T=Rot(Z,γ)Rot(Y,β)Rot(X,α)=

cγ=cosγ　sγ=sinγ

令

在坐标系OXYZ下建立机构每个支链的闭环矢量表达式：

r=ai+bi+lfi-dii=1,2,3

(1)

bi=(0,0,Si)T

式中,r为动平台坐标原点P的位置矢量;ai为静平台上Mi点的位置矢量;bi为静平台上Mi点到转动副R2的中心点Ti的位置矢量;fi连杆Li的单位矢量;di为动平台坐标原点P到各球铰中心a1、a2、a3的位置矢量;Si为各支链上移动副P的输入位移；δi为各支链转动副R1的轴线与X轴正方向的夹角。

设向量u1、u2、u3均为单位向量，u1、u2、u3在Z轴方向上的投影分量分别为sinθ1、sinθ2、sinθ3,在XY平面上的投影分量分别为cosθ1、cosθ2、cosθ3，将cosθ1、cosθ2、cosθ3分解到X轴和Y轴，得到如下向量:

u1=(0,cosθ1,sinθ2)T

由机构的几何特点可知fi⊥ui,对式(1)两端同时点积ui可得到如下约束方程：

lfiui=0i=1,2,3

(2)

由式(1)可得

l=‖r-ai-bi+di‖

(3)

由式(2)可得

(4)

将各已知量代入式(3)展开整理,得到各支链上移动副P的输入位移Si(i=1,2,3)为

(5)

由式(5)可知,Si(i=1,2,3)各有两个根,但球副位于动平台的上方，由于球副转角的限制导致驱动滑块的位置只能处于动平台的上方,因此根号前只能取‘+’。

将取正号的式(5)和各已知量代入式(4),展开整理,可得到输入转角θi(i=1,2,3)为

(6)

对于已知动平台的位姿,则由式(5)、式(6)可以求出各支链输入位移Si(i=1,2,3)和转动副R1的输入转角θi(i=1,2,3)),即求得机构的位置反解。

1.3机构位置正解

位置正解是已知输入位移Si和输入转角θi,求解机器人动平台的位姿(XP,YP,ZP,α,β,γ)。本文通过求得动平台a1、a2、a3三点坐标即可求得动平台位姿。

由于该并联机构的每条支链完全相同,故取其中的一条支链作为研究对象,这里取第一条支链M1T1a1为研究对象。仍以坐标系OXYZ为固定坐标系，以旋转角度θ1后的坐标系T1uvw为局部坐标系,转动副R1的转动轴线为u轴,转动副R2的转动轴线为v轴,w轴根据右手定则确定。

连杆L1与局部坐标系T1xyz的w轴的夹角为φ1。

动坐标系中的任一向量P′都可以通过坐标变换的公式变换到固定坐标系中:

P=TP′+P0

(7)

其中

T=Rot(Z,δ1)Rot(X,θ1)

P′=(-lsinφ1,0,-lcosφ1)T

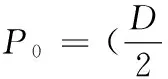
所以可得a1、a2、a3点在坐标系T1xyz中的坐标分别为

(8)

(9)

(10)

因为a1、a2、a3三点中任意两点之间的距离为三角动平台边长，且已知三个边长为定值,故约束方程为

(11)

将式(8)～式(10)代入式(11)，整理可得3个以φi(i=1,2,3)表示的超越方程：

(12)

式中,Ai、Bi、Ci、Di、Ei、Fi、Gi、Hi、Ji(i=1,2,3)均为机构的已知几何参数及各输入变量的函数。

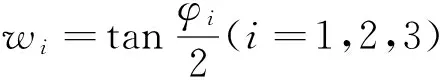
(13)

将式(13)代入式(12),可得代数方程组：

(14)

将式(14)简化成如下形式：

(15)

(16)

(17)

其中,bi、ci、di(i=1,2,3)是式(15)～式(17)中各wi的系数,其本身也含有wi,这样将以φi表示的超越方程变为以wi为未知量的3个方程组。

从式(16)和式(17)中消去w3,得到关于w1和w2的4次方多项式,将该多项式写成关于w2的显式形式：

(18)

(19)

式(19)是关于w1的16次代数方程,由此可解得w1的值,通过式(15)和式(18)逐渐化简可解得w2的值,最后由式(16)和式(17)可得到w3的值。最后即可确定3个点a1、a2、a3在定坐标系下的坐标，最终确定动平台的位姿。

2　数值算例

为了验证上述正反解的理论正确性,给定与处于设计阶段的六自由度并联机床结构参数相同的数据予以证明。选取机构参数如下：静平台直径D=200 mm,动平台直径d=100 mm,支链上连杆长度均为l=100 mm。给定动平台初始位姿

(XP,YP,ZP,α,β,γ)=

(0,10 mm,60 mm,0,0,0)

根据此初始条件得到6个输入为

s1=146.0233 mmθ1=0.1157 rad

s2=150.9177 mmθ2=-0.0549 rad

s3=140.8330 mmθ3=-0.0618 rad

根据已知动平台位姿利用反解求得的6个输入作为初始条件,应用本文的方法进行运动学正解计算,运用MATLAB软件编程求解关于w1的一元十六次方程,共得到16组解，其中在实数范围内共有8组解,这8组解是a1、a2、a3的坐标,通过数学转换可得到动平台中心P点坐标,如表1所示。

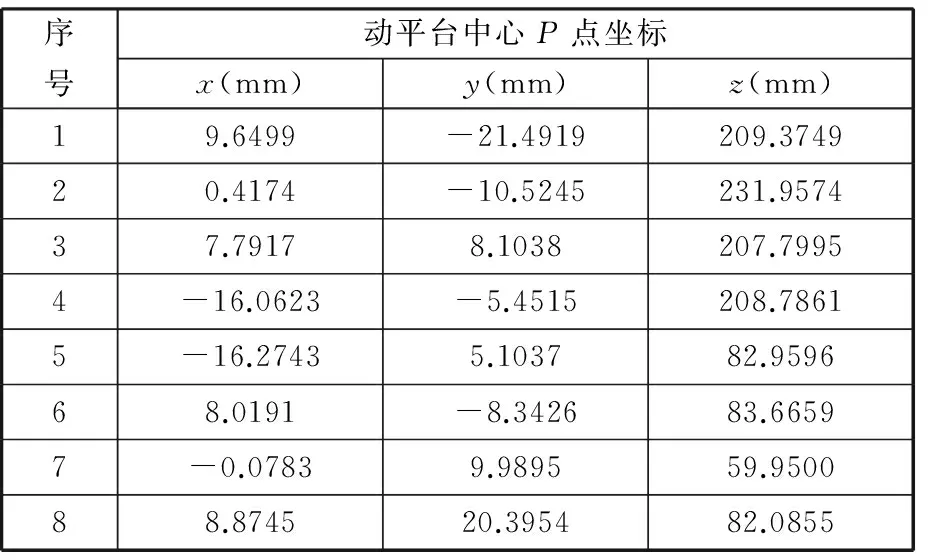
表1　8组实数解对应的动平台中心P点坐标

表1中的8组解即为动平台的位姿。可以看出，第7组解与动平台的初始位姿比较，有微小误差,这主要是由计算的累积误差引起的，总体上是相互吻合的，从而验证了正解的正确性。这8组解对应的机构装配模式如图3所示。其中，经过验证发现，除了第7组解外，其他的动平台位姿均受到球副转角的限制，不符合实际情况。

3　结论

(1)对于应用于虚拟轴并联机床的新型3-PRRS并联机构,本文利用封闭矢量法系统地分析了其运动学求解问题，给出了解析形式的运动学反解。

(2)对于运动学正解，因机构有2个转动副而使机构的分析变得复杂，本文分析支链上2个转动副对动平台的影响,通过坐标变换和引入角度变量φi,推导出动平台三点坐标，建立约束方程，得到只含有3个变量的超越方程，利用消元法并用MATLAB软件编程求解得到全部位置正解，简化了计算步骤，提高了运算速度。

(3)经算例验证，本文解析法是正确且有效的,从而为采用转动副驱动的并联机构提供了一种较为有效的正解解析方法,对于六自由度虚拟轴并联机床的进一步的理论研究及应用都有重要意义。

[1]BechiF.KinematicAnalysisforaSix-DOF3-PRPSParallelMechanism[J].IEEEJournalofRoboticsandAutomation,1988,4(5):561-565.

[2]AlizadeRI,TagiyevNR.AClassofParallelManipulatorsBasedonKinematicallySimpleBranches[J].MechanismandMachineTheory,1994,29(1):115-124.

(a)第1组解(b)第2组解

(c)第3组解(d)第4组解

(e)第5组解(f)第6组解

(g)第7组解(h)第8组解图3　8组解对应的机构装配图

[3]ByunYK,ChoHS.AnalysisofaNovel6-DOF3-PPSPParallelManipulator[J].InternationalJournalofRoboticsResearch,1997,16(6):859-872.

[4]JaimeGD,JerkAR.AnalysisofaSix-degrees-of-FreedomThree-leggedParallelManipulator[J].RoboticsandComputer-IntegratedManufacturing,2012,28(2):220-226.

[5]彭凯.六自由度3-PRPS并联机构的特性理论研究与仿真[D].合肥:中国科学技术大学,2011.[6]冯祥文,金振林,高峰,等.3-URS并联机器人位置分析[J].机械传动,2008,32(5):30-32.

FengXiangwen,JinZhenlin,GaoFeng,etal.PositionAnalysisof3-URSParallelRobot[J].JournalofMechanicalTransmission,2008,32(5):30-32.

[7]MerletJP.ParallelRobots[M].Dordrecht:Springer,2006.

[8]黄真,孔令富,方跃法.并联机器人机构学理论及控制[M].北京:机械工业出版社,1997.

[9]张英,廖启征,魏世民.一般6-4台体型并联机构位置正解分析[J].机械工程学报,2012,48(9):26-32.

ZhangYing,LiaoQizheng,WeiShimin.ForwardDisplacementAnalysisofaGeneral6-4In-parallelPlatform[J].JournalofMechanicalEngineering,2012,48(9):26-32.

[10]黄昔光,廖启征,魏世民,等.一般6-6型平台并联机构位置正解代数消元法[J].机械工程学报,2009,45(1):56-61.

HuangXiguang,LiaoQizheng,WeiShimin,etal.ForwardKinematicsAnalysisoftheGeneral6-6PlatformParallelMechanismBasedonAlgebraicElimination[J].JournalofMechanicalEngineering,2009,45(1):56-61.

[11]王超群,吴洪涛.6-PUS并联机构的运动学正解分析[J].中国机械工程,2013,24(7):853-856.

WangChaoqun,WuHongtao.KinematicsAnalysisof6-PUSParallelMechanism[J].ChinaMechanicalEngineering,2013,24(7):853-856.

[12]何兵,车林仙.载波混沌Newton法在并联机构位置正解中的应用[J].机械传动,2010,34(1):11-15.

HeBing,CheLinxian.ApplicationsofNewtonIterativeMethodofCarrierChaoticMapinForwardPositionalAnalysisofParallelManipulators[J].JournalofMechanicalTransmission,2010,34(1):11-15.

[13]郭宗和,崔荣江,杨启志,等.一种基于PR驱动的6自由度并联机构设计与仿真[J].机床与液压,2012,40(15):105-110.GuoZonghe,CuiRongjiang,YangQizhi,etal.DesignandSimulationofa6-DOFParallelMechanismsBasedonPRDrive[J].HydromechatronicsEngineering,2012,40(15):105-110.

(编辑苏卫国)

Forward and Inverse Position Kinematics Analysis of a New 3-PRRS Parallel Mechanism

Guo Zonghe1Du Qingqing1Yang Qizhi2

1.Shandong University of Technology,Zibo,Shandong,255049 2.Jiangsu University,Zhenjiang,Jiangsu,212013

Kinematics based on a new 6-DOF 3-PRRS parallel mechanism were studied,the analytical form of inverse kinematics was got and closed analytic method was used to study all the forward position solutions.According to the effects of two different revolute pairs on the moving platform,coordinate transformation was used and the angle variablesφiwere introduced to obtain the coordinates of three points on the moving platform.And the constant length between the three points on the moving platform was regarded as the restrict condition to obtain the constrained equations.Then three transcendental equations withφias variables were obtained,and 16 times linear algebraic equation was obtained by elimination method.MATLAB software was used to solve all the forward position solutions.Finally,a numerical example was used to verify the validity of the theories and conclusions.Thus the foundation for dimensional synthesis,singularity analysis,output error analysis and trajectory control of the new 3-PRRS parallel mechanism applied on the virtual-axis hexapod machine was laid.

parallel mechanism;closed analytic method;inverse and forward position kinematics;6-DOF

2013-11-22

国家自然科学基金资助项目(50905077);山东省自然科学基金资助项目(ZR2012EEL05)

TH112DOI：10.3969/j.issn.1004-132X.2015.04.005

郭宗和,男,1961年生。山东理工大学机械工程学院教授、博士研究生导师。主要研究方向为机构学、机器人机构学、变胞机构学。杜晴晴，女，1989年生。山东理工大学机械工程学院硕士研究生。杨启志，男，1974年生。江苏大学机械工程学院教授。