基于滑模的混联仿人空间机械臂轨迹跟踪控制
2015-10-28刘福才梁利环金振林
秦 利 刘福才 梁利环 金振林
燕山大学工业计算机控制工程河北省重点实验室,秦皇岛,066004
基于滑模的混联仿人空间机械臂轨迹跟踪控制
秦利刘福才梁利环金振林
燕山大学工业计算机控制工程河北省重点实验室,秦皇岛,066004
针对空间高速目标抓取任务中对手臂伸出定位基本动作的要求,提出一种4-DOF串并混联仿人机械臂。重点设计了以球面并联机构为机构原型的高承载力肩关节以及轻量化的驱动装置与低惯量的布置形式。考虑混联的结构特点,利用李群李代数法并结合虚功原理推导了机械臂的动力学方程,该方法可避免约束反力的处理与逻辑开链的划分以及大量的微分运算。在此基础上,针对混联结构的强非线性和强耦合性,使用滑模控制器对机械臂进行轨迹跟踪控制,验证了所提滑模控制器的有效性。
混联仿人机械臂;球面并联机构;动力学建模;李群李代数法;滑模控制
0 引言
仿人机器人具有效仿人类的运动机理以及感知协调、思维决策等方面的能力,其应用需求已从传统的工业延伸至航天、军事、医疗等领域。仿人机器人研究的最终目标之一是辅助或替代人类完成诸如外科手术、太空作业、日常服务等复杂、精密、繁重的操作任务。目前,具有代表性的研究成果可大致分为三类[1-3]:ASIMO、HUBO、汇童等仿人机器人,研究重点在于行走能力,臂部操作是辅助研究;HRP-2、Justin等仿人机器人实现了多传感器配合下的臂部基本操作;Cog、DAV等仿人机器人实现了具有自主思维与学习能力的臂部协调操作。上述仿人机器人臂部均为串联结构,执行的操作对机械臂运动精度、速度以及承载能力要求不高。然而,当操作任务具有快速、大负载、高精度等特点时,机械臂的性能则显得十分重要。串联结构具有较大的工作空间,但自由度的增加往往造成关节承载能力的下降和位置累积误差的增大。并联机构具有刚度高、速度快、精度好等优点,但工作空间上难以满足操作要求。相比之下,混联结构可以兼容串并联结构的特点[4],更适应仿人机械臂操作能力方面的要求。现有典型混联仿人机械臂主要有清华大学刘辛军等[5]提出的7-DOF仿人机械臂,燕山大学金振林等[6]设计的6-DOF仿人机械臂,以及上海交通大学SJTU-HR1仿人机器人的臂部[7],研究的侧重点多集中于机构综合与位置分析,动力学分析与控制研究较少[8]。
与串联或并联机械臂不同,串并混联仿人机械臂传动链的结构复杂,具有强耦合性,给其动力学和运动学的分析建模以及轨迹跟踪控制带来很大困难。基于计算力矩的前馈控制方法是实时性较强的一种基本控制方法,但因其鲁棒性不强,往往在存在扰动的情况下难以对机械臂进行有效的控制。而滑模变结构控制作为常用的鲁棒控制方法,对系统的内部及外部扰动均具有很强的鲁棒性,这对于机械臂的控制非常有利,它可以削弱由于随机干扰或负载变化对系统控制性能的影响。所以,机器人控制是近年来滑模变结构控制理论的主要应用环境之一。文献[9]根据控制任务的要求采用基于滑模的控制方法完成了机器人的跟踪任务。文献[10]针对轮式移动机器人的输出跟踪问题,设计了输出跟踪的动态滑模控制器,仿真结果验证了该控制器的良好性能。然而,以上研究只针对串联或并联机械臂,对于串并混联机械臂轨迹跟踪控制的研究较少。
本文针对空间高速目标抓取任务中对手臂伸出定位基本动作的要求,提出一种4-DOF混联仿人机械臂。为解决混联仿人机械臂拓扑结构复杂、动力学求解与控制比较困难的问题,利用虚功原理结合李群李代数的相关运算公式,建立了形式简洁、便于工程实现的动力学方程,针对动力学方程的强非线性的特点,使用滑模控制器对其动力学进行了轨迹跟踪控制的仿真和分析,为混联仿人机械臂的动力学分析与控制提供了新方法。
1 机构描述
1.1结构布局说明
人类手臂具有高度的灵活性与冗余性。对于手臂自由度的分布,Mark[11]认为肩部3个自由度、肘部1个自由度、腕部3个自由度,这是目前仿人手臂采用较多的构型。神经生理学研究结论表明臂部与手部姿态相互独立,腕部位置是由肩、肘两关节确定的[12]。因此,对于高速目标抓取任务中手臂伸出定位基本动作的研究,重点是肩、肘部的设计。故而选择本文所提混联仿人机械臂的自由度布局为:肩部3个自由度,肘部1个自由度,暂不涉及腕关节。
肩部为典型的球窝关节,需承载悬臂的自重及外部负载,是手臂中最灵活且受力最大的部位。而球形关节在构件结构与驱动方式的实现上都比较复杂,多以串联形式将3个自由度分开实现,关节负载能力非常有限。观察人类肩部结构,肩部内收/外展的运动范围最大,直接限制臂部的工作空间。而承载最大的是与重力指向相同的伸/屈方向运动。
基于以上生理结构、承载能力与工作空间的综合分析,选择该机械臂传动链结构为:以转动副实现肩部内收/外展(即偏航方向)运动,以一种5个转动副构成的2-DOF球面并联机构(以下简称5R 2-DOF SPM)实现伸/屈(即俯仰方向)和内/外旋(即横滚方向)两个方向的运动,肘部采用一转动低副,肩部、大臂、肘部、小臂串接。图1是该机械臂的Solidworks装配图。5R 2-DOF SPM的装配图见图2。5R 2-DOF SPM包含2个主动杆、2个从动杆和5个转动副。如图2所示,该机构各转动副轴线相交于机构转动中心o2且每条运动支链上相邻转动副轴线两两垂直。整个机构由两条运动支链构成,支链1(简称D1)为Rs1→L1→Rs3→L3→Rs4→L4,支链2(简称D2)为Rs2→L2→Rs5。
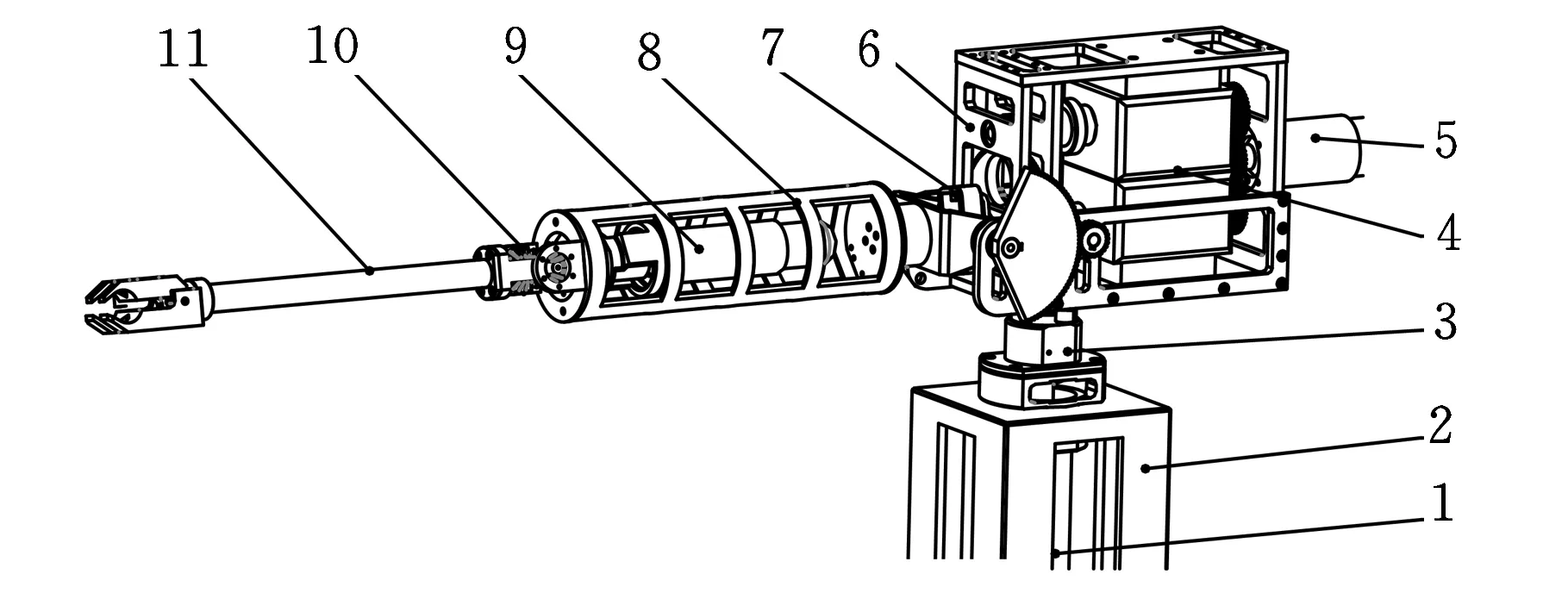
1.肩部驱动装置1 2.基座 3.机架及驱动装置连接件 4.上下离合器 5.肩部驱动装置2 6.肩部固件 7.5R 2-DOF SPM 8.大臂 9.肘部驱动装置 10.肘部 11.小臂图1 机械臂整体装配图

图2 5R 2-DOF SPM机构装配图
肩部驱动装置1驱动与基座连接的转动副,控制肩部在偏航(yaw)方向的转动;肩部驱动装置2经由上下离合器及齿轮啮合通过转动副Rs1和Rs2分别驱动主动杆L1和L2,通过支链1实现L4的横滚(roll)运动,支链2实现L2的俯仰(pitch)运动。大臂连接件穿过与L2固连的Rs5与L4固接,从而将5R 2-DOF SPM输出的俯仰和横滚两方向的旋转运动传递给大臂;小臂经由肘部转动副与大臂相串联,由肘部驱动装置控制实现俯仰方向的运动。
该混联仿人机械臂在设计上有以下几个优点:①并联结构使累计误差更小,精度更高;②两组驱动装置经由并联结构共同承载悬臂及末端负载,使肩部承载能力提高;③肩部驱动装置放置于肩部固件上,减小了运动构件的质量和驱动装置的自重载荷;④肘部驱动装置内嵌于中空的大臂中,避免置于杆件外部,从而降低了运动惯性,提高了机械臂的动态特性;⑤5R 2-DOF SPM为正交并联机构,加工精度更高。
1.2坐标系建立及位置分析
设系统的广义坐标为q=(q1,q2,q3,q4)T,各关节坐标系设置如图3所示。系{0}-o0x0y0z0为基坐标系,系{2}-o2x2y2z2为5R 2-DOF SPM固定坐标系,系{3}-o3x3y3z3为5R 2-DOF SPM随动坐标系,系{4}-o4x4y4z4为肘关节坐标系,系{5}-o5x5y5z5为末端坐标系。系{2}与系{3}原点重合于5R 2-DOF SPM的转动中心,z3与Rs5轴线重合,x3与Rs4轴线重合,从而,5R 2-DOF SPM俯仰方向的输出是z3正向与y2负向的夹角,横滚方向的输出是x3正向与x2负向的夹角。
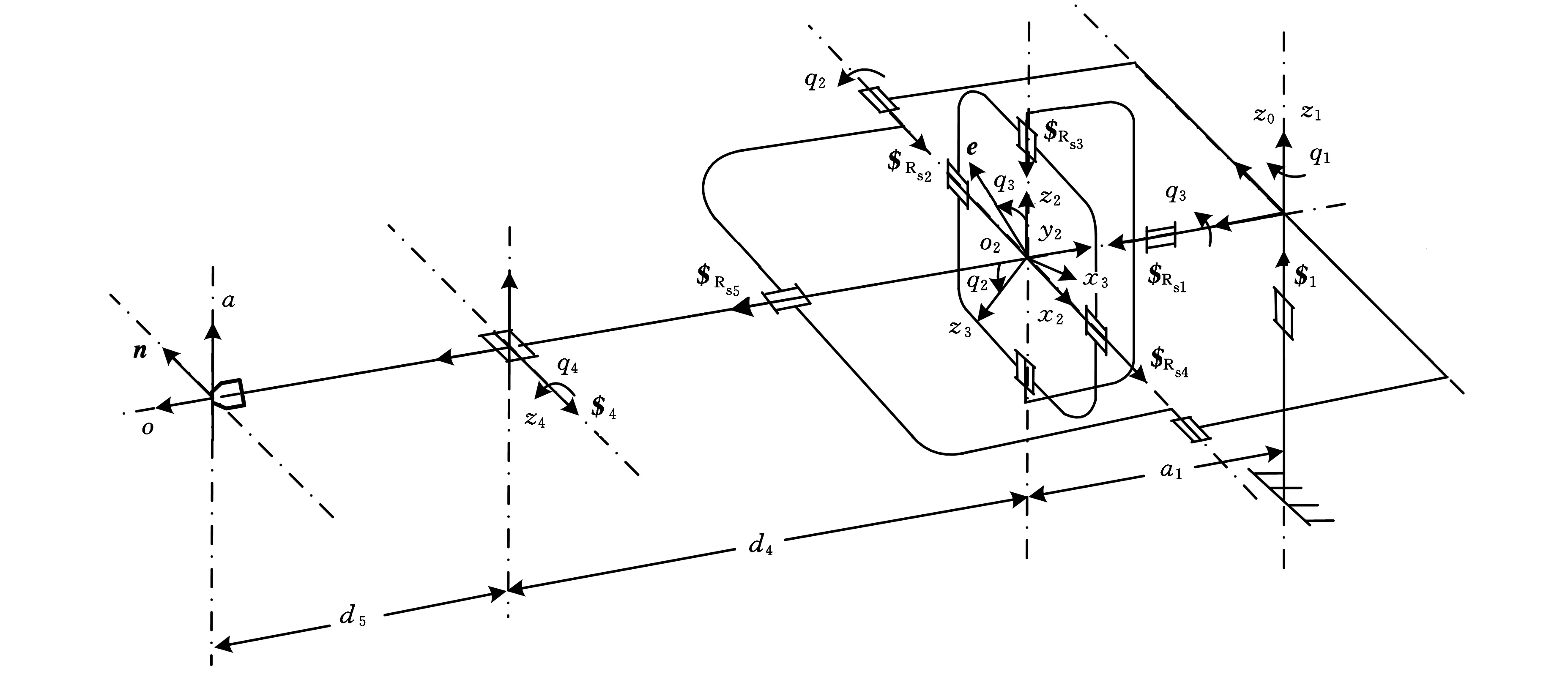
图3 机械臂坐标系示意图
设单位矢量e与Rs3轴线重合,根据5R 2-DOF SPM各传动链中相邻转动副轴线垂直的特点,容易得到几何关系:x3=e×z3,y3=z3×x3。从而求得系{3}的坐标轴单位矢量x3、y3、z3在系{2}中的表达式:
(1)

从而,可以得到系{3}到系{2}的变换矩阵A3=[x3y3z3]。使用D-H法可求得系{1}到系{0}的变换矩阵A1,系{2}到系{1}的变换矩阵A2,系{4}到系{3}的变换矩阵A4,末端到系{4}的变换矩阵A5,计算T=A1A2A3A4A5,可得末端坐标系到基系的变换矩阵与正运动学模型的解析解。同理可求得各关节位置在基系中的解析解。
2 动力学分析及建模
混联仿人机械臂动力学分析的难点是闭环与被动关节的处理,目前主要的处理方法是,利用符号推导等方式将混联传动链的闭环切开等效为串联结构[13]。传统动力学建模方法主要有Lagrange法与Newton-Euler法,前者形式简单,但需大量微分运算,计算复杂度为O(N4);后者计算复杂度为O(N),但被动关节导致未知运动学参数的存在,令推导过程复杂。李群李代数法由于其物理意义明确、表达形式简洁而被应用于多体系统的分析中,以往的应用主要是利用伴随映射改进开链递推公式[14],以及利用驱动螺旋理论对并联机构建模[15]。本文的应用重点在于处理混联传动链中的被动关节,得到简洁的动力学解析解。求解思路如下:利用螺旋理论的结论公式将被动关节的运动学参数表示为驱动关节相关参数的组合,并应用李代数伴随算子和对偶伴随算子实现其不同坐标系中的变换,整理出连杆质心速度螺旋系数的计算式;然后应用Klein内积使开链和闭链中的连杆具有统一形式的动力学表达式;最后利用虚功理论推导出只包含连杆力螺旋与质心速度螺旋的表达式,从而得到计算复杂度低的动力学解析解。具体计算方法如下。
写出图3所示基座、肘关节转动副螺旋$i(i=1,4)以及5R 2-DOF SPM各转动副螺旋$Rsj(j=1,2,…,5)的Plücker坐标:
(2)
设ωRsj(j=1,2,…,5)为转动副Rsj(j=1,2,…,5)的角速度,利用开环速度螺旋递推公式[16]可分别列出并联机构输出速度VL4在支链D1及D2中的表达式,整理后可得关于ωRsj的非齐次线性方程组:
(3)
求解上式,便可得到用广义关节速度的线性组合表示的被动关节角速度:
(4)

基于式(4)进一步可得并联机构各连杆速度螺旋VL n:
(5)
进一步推导可得基系螺旋系数$*0与刚体坐标系螺旋系数$*的关系式:
(6)
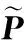
以及连杆Δ的质心速度螺旋系数$Δcm*与其开环速度螺旋系数$*0之间的关系式:
$Δcm*=[P($*0)P($*0)×rΔcm+D($*0)]T
(7)
式中,rΔcm为连杆质心位矢在基系中的表达。
利用式(5)~式(7)可得各杆件质心速度螺旋在基系中的表达:
(8)
式中,Vscm为肩部整体的速度螺旋;Vuacm为大臂的速度螺旋;Vfacm为小臂的速度螺旋;VLncm(n=1,2,3,4)为并联机构各连杆的速度螺旋。
刚体受到的力螺旋[16]对刚体做的功可由李代数的Klein内积计算得出,则系统总功W的表达式为
W=KL(Vscm,Fs)+KL(Vuacm,Fua)+KL(Vfacm,Ffa)+
KL(VL1cm,FL1)+KL(VL2cm,FL2)+
KL(VL3cm,FL3)+KL(VL4cm,FL4)+
(9)
式中,τi为关节驱动力矩;Fs为肩部整体受到的力螺旋;Fua为大臂受到的力螺旋;Ffa为小臂受到的力螺旋;FL i(i=1,2,3,4)为并联机构各连杆受到的力螺旋;KL(·)表示Klein内积运算。
假设机构处于平衡状态时驱动关节速度为0,根据虚功定理可得系统动力学方程:
(10)
进而可得驱动力矩表达式,写为矩阵形式为

(11)
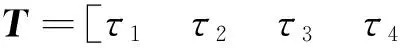
3 控制器设计
由于该混联仿人机械臂具有串并混联的结构特点,其动力学模型具有很强的非线性,当使用常规的PD或PID进行关节空间轨迹跟踪控制时,很难达到控制任务的要求,为此,设计滑模控制器。具体分析与设计如下。
变换系统动力学模型式(11),可得
(12)
若考虑系统的扰动则系统的动力学模型可写为
(13)
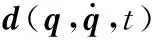
定义系统的跟踪误差为
e=qd-q
(14)
(15)
式中,qd和q分别为系统期望和实际的关节位置矢量。
选取滑模面如下:
(16)
式中,KP∈R4×4为正定比例增益矩阵;KI∈R4×4为正定积分增益矩阵;KD∈R4×4为正定微分增益矩阵。
对式(16)求导并将式(12)和式(13)代入得
(17)
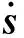
(18)
为抑制控制器输出抖动,使用饱和函数作为趋近率,则切换控制律设计为
Ts=Krsat(s/ki)
(19)
式中,Kr为正定对角矩阵;ki为正常数;sat(·)为饱和函数。则系统的控制律为
T=Teq+Ts
(20)
取李雅普诺夫函数为
(21)
对V(t)求导可得
(22)
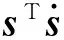
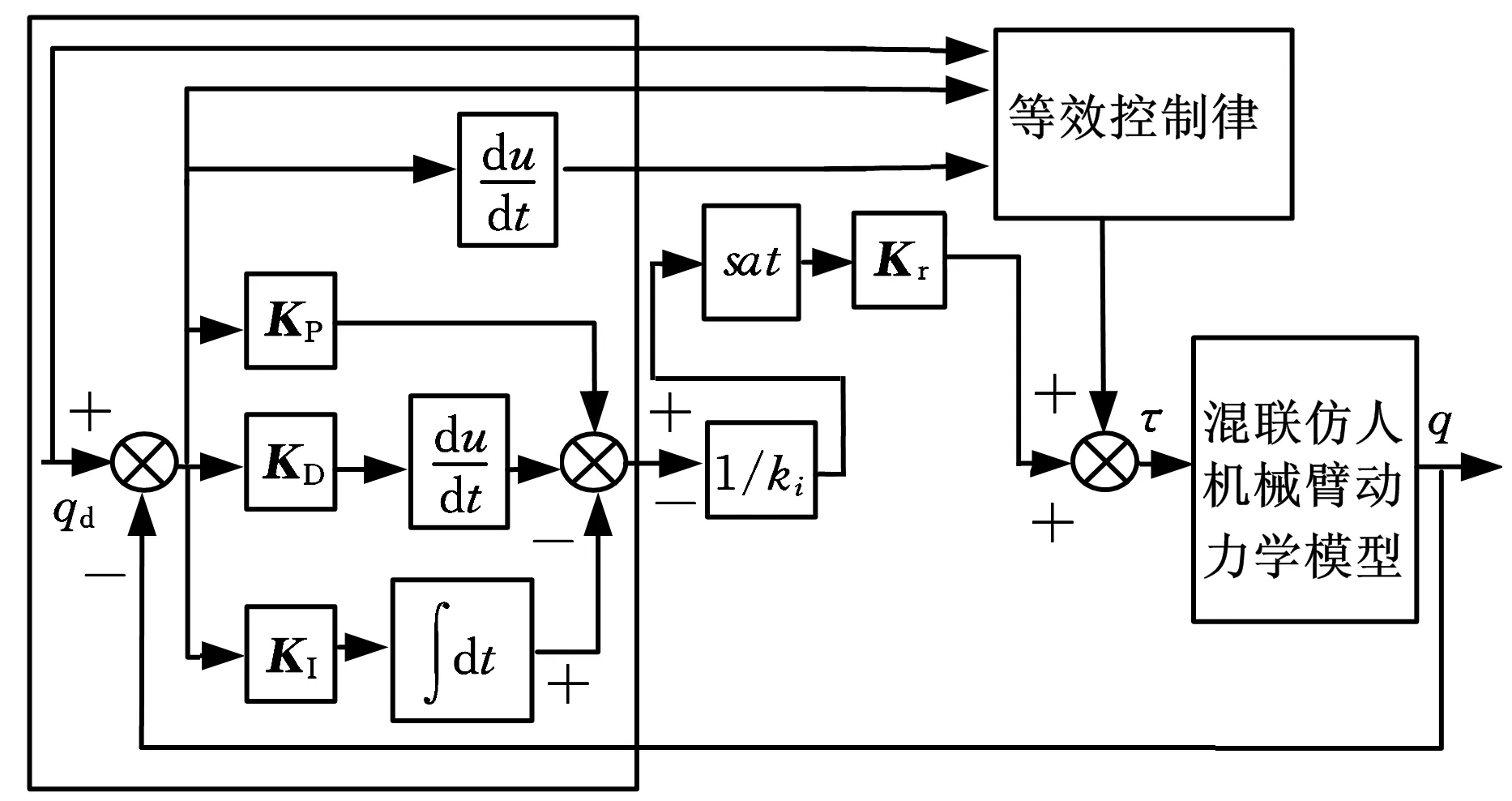
图4 混联仿人机械臂滑模控制系统框图
4 仿真研究
为了验证本文所设计控制方法的有效性,使用控制器式(20)对该混联仿人机械臂进行轨迹跟踪控制仿真研究。控制器参数为:KI=diag(1000,1200,1200,1200),KD=diag(4,4,4,4),ki=100,KP=diag(100,80,80,80),Kr=diag(1.5,1.5,1.5,1.5)。系统仿真参数如表1所示(表中,a1、d4、d5含义见图3)。仿真环境为MATLAB 7.0,仿真时间为10 s,仿真结果如图5、图6所示。

表1 仿真实验参数表

(a)关节空间期望轨迹与实际轨迹对比图
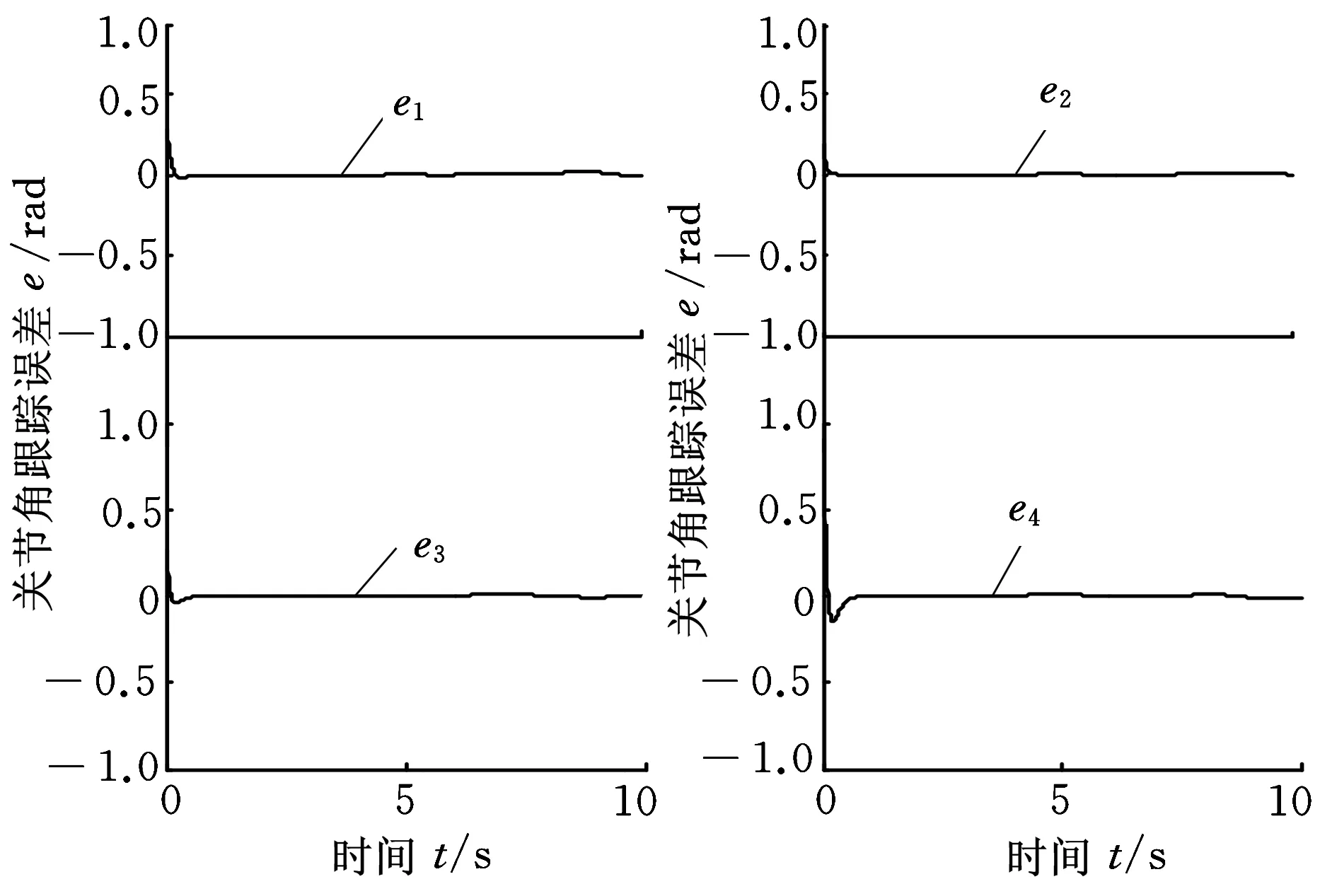
(b)关节空间跟踪误差

(c)工作空间期望轨迹与实际轨迹对比图
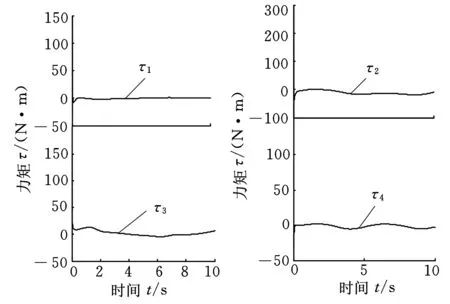
(d)关节驱动力矩图5 无扰动时滑模控制仿真结果

图6 有扰动时工作空间期望轨迹与实际轨迹对比
使用PD控制器对混联仿人机械臂进行轨迹跟踪控制时,即使无外界扰动,系统也最终发散,无法稳定运行,由此可以说明串并混联机械臂控制的复杂性及所提控制方案的优点。
5 结语
针对未来空间自主在轨服务的任务需求,在分析人类手臂结构及运动机理的基础上,提出了一种以2-DOF球面并联机构串联转动低副布置传动链的新型4-DOF串并混联仿人机械臂,该机械臂结构紧凑、位置分析简单、承载能力好,且不存在移动副,更便于控制与维护。在动力学建模方面,阐述了闭环与被动关节的处理方法,以及利用虚功原理与Klein算子的动力学推导过程,并给出质心速度螺旋系数的计算公式。最后应用该动力学解析解,设计了滑模控制器对其进行轨迹跟踪控制,通过与PD控制进行对比说明串并混联机械臂控制的复杂性且突出了滑模控制器的优越性。研究结果为同类型混联机构的设计、分析以及应用研究提供了经验。下一步的研究工作将分析该机械臂在不同重力环境下的动力学特性与控制问题。
[1]Park Ill-Woo,Kim Jung-Yup,Lee Jungho,et al.Mechanical Design of the Humanoid Robot Platform,HUBO[J].Advanced Robotics,2007,21(11):1305-1322.
[2]Wimbock T,Nenchev D,Albu-Schäffer A,et al.Experimental Study on Dynamic Reactionless Motions with DLR’s Humanoid Robot Justin[C]//IEEE/RSJ International Conference on Intelligent Robots and Systems. St. Louis:IEEE,2009:5481-5486.
[3]李允明. 国外仿人机器人发展概况[J]. 机器人, 2005, 27(6): 561-568.
Li Yunming.Foreign Status of Humanoid Robot[J].Robot,2005, 27(6): 561-568.
[4]高征,肖金壮,王洪瑞,等.一种三自由度串并联结构旋转台的动力学分析[J].中国机械工程,2012,23(1):18-21,38.
Gao Zheng,Xiao Jinzhuang,Wang Hongrui,et al. Dynamics Analysis on a 3-DOF Rotational Platform with Serial-Parallel Structure[J].China Mechanical Engineering, 2012,23(1):18-21,38.
[5]刘辛军,汪劲松,高峰,等.一种串并联结构拟人七自由度冗余手臂的设计[J]. 中国机械工程, 2002,13(2): 101-104.
Liu Xinjun,Wang Jingsong,Gao Feng,et al.Design of a Serial-Parallel 7-DOF Redundant Anthropomorphic Arm[J]. China Mechanical Engineering, 2002,13(2): 101-104.
[6]金振林, 李研彪, 王跃灵.一种新型6-DOF串并混联拟人机械臂及其位置分析[J]. 中国机械工程, 2009, 20(3): 280-284.
Jin Zhenlin,Li Yanbiao,Wang Yuelin.A Novel 6-DOF Hybrid Anthropopathic Mechanical Arm and Its Position Analysis[J]. China Mechanical Engineering, 2009, 20(3): 280-284.
[7]Yang J L,Gao F.Classification of Sitting States for the Humanoid Robot SJTU-HR1[J]. Journal of Bionic Engineering,2011, 8: 49-55
[8]Doina P,Andras S,Calin V,et al.Kinematics and Workspace Modeling of a New Hybrid Robot Used in Minimally Invasive Surgery[J].Robotics and Computer-Integrated Manufacturing,2013,29(2):463-474.
[9]Fabricio G,Luis G,Antonio S,et al.Sliding Mode Speed Auto-regulation Technique for Robotic Tracking[J].Robotics and Autonomous Systems,2011,59(7/8):519-529.
[10]晁红敏,胡跃明.动态滑模控制及其在移动机器人输出跟踪中的应用[J].控制与决策,2001,16(5):565-568.
Chao Hongmin,Hu Yueming.Dynamical Sliding Mode Control and Its Applications to Output Tracking of Mobile Robots[J].Control and Decision,2001,16(5):565-568.
[11]Mark E R.Robot Evolution:the Development of Anthrobotics[M]. Hoboken: John Wiley & Sons Inc, 1994.
[12]Asfour T,Azad P.Imitation Learning of Dual-arm Manipulation Tasks in Humanoid Robots[J].International Journal of Humanoid Robotics,2008,5(2):183-202.
[13]黄玉钏,曲道奎,徐方.基于自然正交补的真空机器人动力学建模[J].机器人,2012,34(6):730-736.
Huang Yuchuan,Qu Daokui,Xu Fang.Dynamic Modeling of Vacuum Robots Based on Natural Orthogonal Complement[J].Robot,2012,34(6):730-736.
[14]Ibrahim O,Khalil W.Inverse and Direct Dynamic Models of Hybrid Robots[J].Mechanism and Ma-
chine Theory,2010,45(4):627-640.
[15]邵兵,吴洪涛,程世利,等.基于李群李代数的主被动关节机器人动力学及控制[J].中国机械工程,2010,21(3):253-257.
Shao Bing,Wu Hongtao,Cheng Shili,et al.Dynamics and Control of Robot with Active and Passive Joints Using Lie Groups and Lie Algebras[J].China Mechanical Engineering,2010,21(3):253-257.
[16]Gallardo J,Rico J M,Frisoli A,et al.Dynamics of Parallel Manipulators by Means of Screw Theory[J].Mechanism and Machine Theory,2003,38(11):1113-1131.
(编辑苏卫国)
Hybrid Humanoid Space Mechanical Arm Trajectory Tracking Control Based on Sliding Mode
Qin Li Liu FucaiLiang LihuanJin Zhenlin
Key Lab of Industrial Computer Control Engineering of Hebei Province,Yanshan University,Qinhuangdao,Hebei,066004
To study the reaching motion of arm in high-speed target grasp tasks,a 4-DOF hybrid humanoid space mechanical arm was presented.The design of the shoulder joint with high bearing capacity which was based on spherical parallel manipulator,light weight device drivers and layout form with low moment of inertia were stressed on.Considering the structure characteristics of hybrid mechanism,the dynamics analyses were investigated using the principle of virtual work and Lie group and Lie algebra.This method can avoid the processing of constraint reaction and the division of logic open-chains and a lot of differential operations.The trajectory tracking task was completed by using the sliding mode control(SMC) which could cope with the high nonlinearity and couplings of the hybrid humanoid space mechanical arm. Simulation results show the effectiveness of the SMC.
hybrid humanoid mechanical arm;spherical parallel manipulator;dynamics modeling;Lie groups and Lie algebra;sliding mode control
2013-07-03
国家高技术研究发展计划(863计划)资助项目
TP242.2DOI:10.3969/j.issn.1004-132X.2015.04.002
秦利,女,1984年生。燕山大学电气工程学院博士研究生。主要研究方向为机器人技术、智能控制。刘福才(通信作者),男,1966年生。燕山大学电气工程学院教授、博士研究生导师。梁利环,女,1990年生。燕山大学电气工程学院硕士研究生。金振林,男,1962年生。燕山大学机械工程学院教授、博士研究生导师。
