分布式天基雷达动目标检测性能分析

李延 张庆君 刘亚东 刘久利

（北京空间飞行器总体设计部，北京 100094）

分布式天基雷达动目标检测性能分析

李延 张庆君 刘亚东 刘久利

（北京空间飞行器总体设计部，北京 100094）

针对多部天基雷达采用分布式工作体制检测运动目标面临的杂波抑制困难问题，分析了沿航迹基线长度、有效基线长度、地面坡度、波束指向误差、图像配准误差、通道幅度和相位误差对杂波抑制和动目标检测性能的影响。仿真实验结果为以动目标检测为目的的卫星编队构形和雷达参数选择提供了一定依据。

天基雷达；卫星编队构形；杂波抑制；动目标检测

1 引言

多部天基雷达协同工作，具备多基线、多视角观测能力，在合成孔径雷达成像、高程测量等雷达成像遥感方面应用潜力巨大，是近年来的研究热点［1-2］。尤其在地面运动目标检测方面，多部天基雷达存在长的沿航迹基线，能克服传统单平台天基雷达天线口径难以做大的难题，有利于获得更好的最小可检测速度。不过，不同的雷达观测视角和通道响应特性导致回波相关性下降；长的沿航迹基线导致动目标速度估计高度模糊（盲速就是零速模糊），速度响应特性非常细碎［3］。只有在合理设计和保持编队构形和系统参数的基础上，多部天基雷达在地面运动目标检测方面的优势才能充分发挥。

众所周知，运动目标检测的最优构形是多部天基雷达沿航向直线排列。但是，地球自转和卫星轨道摄动等实际因素导致多部天基雷达严格地沿航向分布很难实现，不可避免地存在与雷达观测视线垂直的分量（称为有效基线）。有效基线一方面导致雷达观测视角存在差异，另一方面引入与地形有关的高程干涉相位，给杂波抑制和动目标参数估计带来困难。特别在有效基线较长或地面坡度较大情况下，抑制杂波和检测运动目标尤为困难。除去有效基线外，沿航迹基线、波束指向误差、通道幅度和相位都影响回波相关性。回波相关性越低，抑制杂波后的剩余就越大，在相同判决门限下虚警概率会增大。图像配准误差不影响数据内在相关性，采用图像域多像素自适应处理方法可忽略它对杂波抑制性能的影响，但它导致无法正确匹配动目标信号，杂波抑制后的输出信杂噪比下降。

针对上述问题，本文通过仿真实验重点分析了沿航迹基线长度、有效基线长度、地面坡度、波束指向误差、图像配准误差、通道幅度和相位误差对杂波抑制和动目标检测性能的影响，该研究仿真结果已应用于我国后续规划的具有动目标监测功能卫星论证中，为系统编队构形和雷达参数的选择提供了有力支撑。

2 分析模型

对于动目标检测的基础是对杂波进行有效的抑制，按照最大似然准则，自适应匹配滤波器可以获得最大的信噪比（SNR）和信杂比（信号/杂波，SCR）。本文以自适应匹配滤波器为基础，在考虑各实际因素下对输出的信噪比和信杂比进行了仿真分析。基于线性约束最小方差准则的最优权矢量可以写为［4］

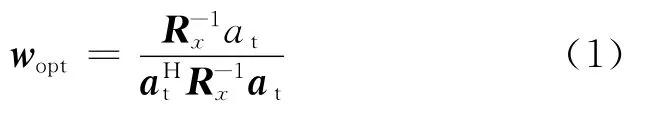
用最优权矢量作用于数据即可消去与动目标信号矢量正交的杂波成分，使其输出信杂噪比（（信号/杂波）/噪声）达到最大。自适应处理器性能可采用改善因子损失进行衡量。定义改善因子损失为：实际输出信杂噪比与高斯白噪声情况下采用匹配处理的输出信噪比之比。即

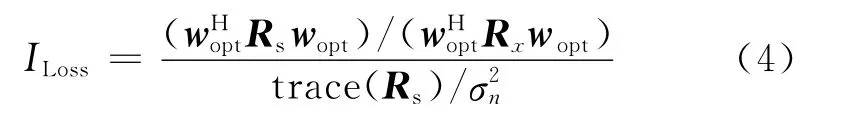
式中：Rs是动目标信号的相关矩阵。

对于天基预警雷达，由于相干处理时间短，可以假设相干积累时间内雷达阵列和散射体之间的几何关系不变，对于运动目标，方位-多普勒轨迹是一个点。当地面动目标仅有切向速度时，动目标回波信号多普勒调频斜率发生变化，从而导致动目标谱相对于杂波谱有一定角度的旋转；当地面动目标仅有径向速度时，动目标回波信号多普勒中心频率不为零，导致动目标谱相对于杂波谱在多普勒频率上有平移；而当动目标具有切向速度和径向速度时，其动目标谱具有旋转和平移的特性。

3 影响因素

多部天基雷达构成的系统可视为多通道系统，影响杂波抑制性能的主要因素是雷达回波数据之间的相关性。就分布式天基雷达系统而言，去相干源可以大致分为以下几类：信噪比去相干γSNR、空间基线去相干γspa、配准去相干γreg、通道失配去相干γm、体散射去相干γvol和时间去相干γt。最后，总的相干系数可表示为γ=γSNR·γspa·γreg·γm·γvol·γt（信噪比即为杂噪比）［5-6］（杂噪比为杂波/噪声，CNR）。

体散射去相干通常存在于复杂场景中，例如城市或城郊结合部。杂波时间去相干通常对单星双航过影响较大，而分布式天基雷达采用多星单航过方式且相距较近。因此我们可以暂不考虑体散射去相干和时间去相干的影响［7-8］。

假设两部分布式星载雷达的信噪比相同，信噪比去相干可表示为

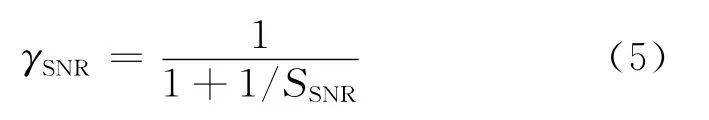
式中：SSNR为信噪比。

空间基线去相干主要由沿航迹基线去相干和有效基线去相干两部分构成，即γspa=γat·γct。沿航迹基线去相干（方位向去相干）可表示为

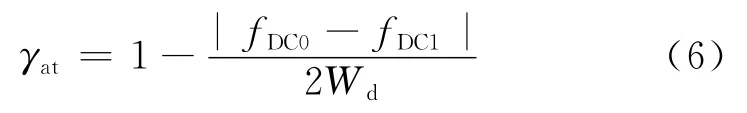
式中：fDC0和fDC1分别表示发射星和接收星接收信号的多普勒中心频率；Wd为多普勒带宽。

定义ρr为距离向分辨率；λ为波长；θ1为发射星的入射角；θ2为接收星的入射角；ψ1和ψ2分别为发射星和接收星的距离高度平面与轨道平面间的方位二面角，则有效基线去相干可表示为［9-10］

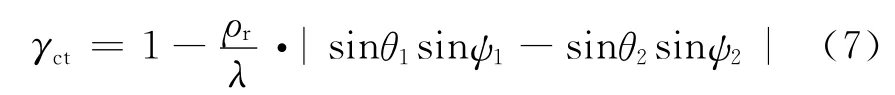
配准去相干包括图像方位配准去相干和距离配准去相干，即可表示为γreg=γrega·γregr。考虑方位向配准误差为Δx，距离向配准误差为Δr，方位向分辨率为ρa，则方位向配准去相干为

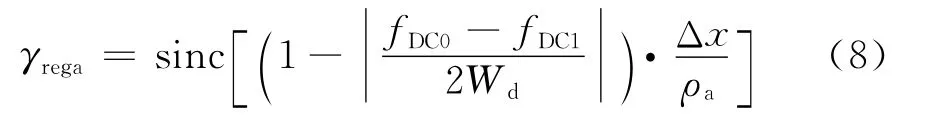
距离向配准去相干为

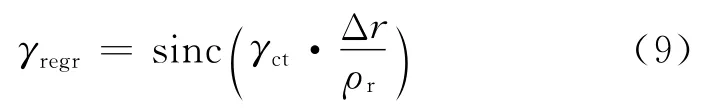
通道失配主要指不同通道存在随机响应误差。假设该误差能够采用随机幅度/相位误差模型表示，可以推导出由通道幅度和相位误差导致的去相干为

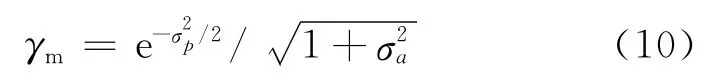
式中：σ2a表示幅度误差；σ2p表示相位误差。

除去上述导致回波相关性下降的因素外，Rx的估计误差和目标导向约束偏差都会影响自适应处理输出信杂噪比。其中Rx的估计误差主要受训练样本的一致性影响，目标导向约束偏差主要受通道失配和配准误差影响。特别在具有较长有效基线情况下，杂波导向矢量对地物的高程变化非常敏感，样本的一致性变差，难以获得有效的Rx估计值。

4 仿真实验

通过方位和距离预滤波补偿处理能够有效克服空间去相干影响，但距离预滤波要求整个观测场景平坦或满足相同坡度，并且方位预滤波潜在地会导致动目标丢失，因此，在杂波抑制性能仿真分析中可忽略垂直基线导致平坦场景去相干影响，但需要考虑垂直基线导致的坡地去相干影响和方位向去相干影响。仿真参数如下：雷达工作波长0.03 m，轨道高度500 km，下视角35°，距离分辨率5 m，方位分辨率5 m，输入信杂比为4 d B，杂噪比为8 dB。

下面首先分析有效基线和地面坡度对改善因子损失的影响。图1给出了地形为平坦地面以及一定坡度情况下运动目标检测输出信杂噪比损失情况。从图1中可以看出，5°以内的小斜坡，在有效基线小于245 m的情况下，有效基线引起的样本非均匀不明显，选择足够的距离向样本（60个左右）构造协方差矩阵进行杂波抑制，输出信杂噪比损失可控制在3 d B左右。但是选取过多的距离向样本则会造成杂波样本非均匀，输出信杂噪比下降。对于较大的坡度（例如20°），在有效基线80 m时，地面坡度造成的样本非均匀已经比较明显，导致无法正确估计杂波协方差矩阵，信杂噪比损失严重。需要指出的是，假如对地形情况有一定的先验知识，可以根据已有的先验知识对坡度进行补偿。

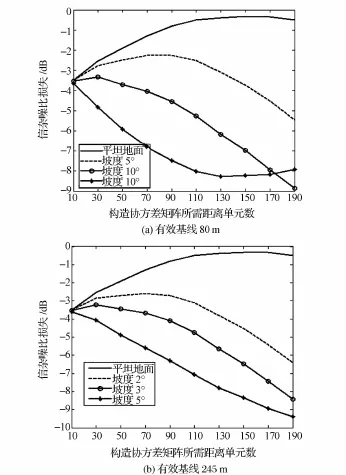
图1 有效基线及坡度对改善因子损失的影响Eig.1 Effect of effective baseline on improvement factor

就平坦或坡度连续变化的自然场景，在SAR图像域通过信号处理方法可平滑掉与高程有关的干涉相位。对于地面的那些高程起伏的孤立目标（例如房屋、树木、电线杆等）和坡度非连续变化区域，由于无法有效补偿其与高程有关的干涉相位而潜在地会误判别为运动目标，造成虚警［11-12］。图2给出了杂噪比14 dB情况下不同有效基线对高程起伏孤立杂波的抑制性能。可见发现：若要求对高程起伏孤立杂波抑制能力优于10 d B，在有效基线长度（B）大于50 m时孤立杂波高程起伏不能超过10 m；否则会因为无法有效抑制高程起伏杂波而增大虚警概率［13-14］。

图3给出了在坡度误差5°、通道幅度/相位均方根误差1 dB/0.2 rad、目标导向矢量与杂波导向矢量正交情况下的改善因子损失与沿航迹基线的变化关系。可以发现：沿航迹基线长度增加后，改善因子损失增大，原因在于沿航迹基线导致的方位去相干随着沿航迹基线长度的增加而增加［15-16］。

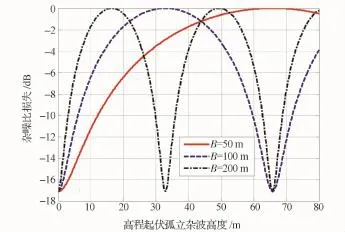
图2 杂噪比损失随着高度变化关系Eig.2 Relation of improvement factor loss and along track baseline

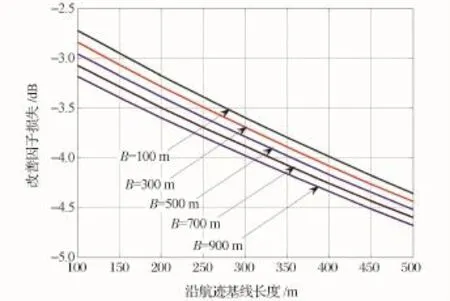
图3 改善因子损失与沿航迹基线长度的变化关系Eig.3 Relation of improvement factor loss and along track baseline

图4给出了沿航迹基线100 m、有效航迹基线100 m、坡度误差5°，目标导向矢量与杂波导向矢量正交情况下的改善因子损失与通道幅度/相位均方根误差的变化关系。可以发现：通道幅度误差从0.5 d B增大到1 d B对改善因子损失的影响不明显，主要原因是仿真分析中设定的杂波噪声功率比较低（只有8 d B）所致；相位误差对改善因子损失的影响更为显著。

不同卫星的波束指向误差同样会导致观察场景的多普勒谱发生移动，考虑地面运动目标检测不能够采用方位预滤波处理，因此波束指向误差导致的去相干影响是我们采用信号处理的方法所不能克服的［17-18］。图5给出了沿航迹基线100 m、坡度50、目标导向矢量与杂波导向矢量正交的改善因子损失与波束指向误差的变化关系。

通过采用自适应处理方式可以克服图像配准误差对杂波抑制性能的影响，但图像配准误差会导致无法正确约束目标导向矢量，即无法对目标进行匹配处理，因此图像配准误差会导致改善因子下降。图6给出了沿航迹基线100 m、坡度50、无波束指向误差、目标导向矢量与杂波导向矢量正交时图像配准误差对改善因子损失的影响［19-20］。

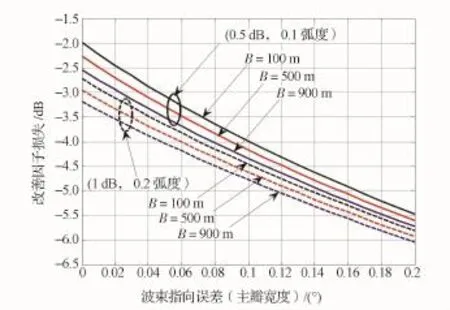
图5 改善因子损失与波束指向误差的变化关系Eig.5 Relation of improvement factor loss and beam-pointing error

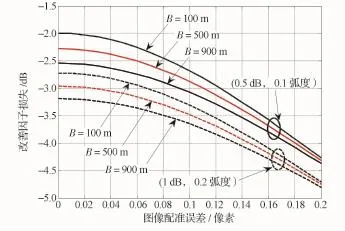
图6 改善因子损失与图像配准误差的变化关系Eig.6 Relation of improvement factor loss and image registration error

5 结束语

本文通过建立分布式天基雷达性能分析模型，仿真分析了沿航迹基线长度、有效基线长度、地面坡度、波束指向误差、图像配准误差、通道幅度和相位误差对杂波抑制和动目标检测性能的影响。仿真结果表明：对于连片近似平坦杂波背景，要求沿航迹基线长度小于200 m、有效基线长度小于100 m、通道幅度/相位均方根误差小于0.5 dB和0.1 rad、坡度小于5°、波束指向误差控制在1/20个主瓣宽度、图像配准误差控制在1/20个像素则改善因子损失小于4 dB；对于具有一定高程起伏的孤立杂波，有效基线长度大于50 m时，杂波高程起伏超过10 m就会造成虚警。

（

）

［1］Goodman N A，Lin SC，Rajakrishna D，et al.Processing of multiple-receiver spaceborne arrays for wide-area SAR［J］.IEEE Transactions on Geoscience and Remote Sensing，2002，40（4）：841-852

［2］Massonnet D.Capabilities and limitation of the interferometric cartwheel［J］.IEEE Transactions on Geoscience and Remote Sensing，2001，39（3）：506-520

［3］Lo M W.Satellite-constellation design［J］.Computing in Science&Engineering，1989（1）：58-66

［4］M V Dragosevi，W Burwash，S Chiu.Detection and estimation with RADASAT-2 moving-object detection experiment modes［J］.IEEE Trans.on GPS，2012，50（9）：3527-3543

［5］Zebker H A，Villasenor J.Decor relation in interferometric radar echoes［J］.IEEE Transactions on Geoscience and Remote Sensing，1992，30（5）：950-959

［6］Gatelli J，Guarnieri A M.The wave number shift in SAR interferometry［J］.IEEE Transactions on Geoscience and Remote Sensing，1994，32（4）：855-865

［7］J Mittermayer，G Krieger，A Moreira，et al.Interferometric performance estimation for the interferometric Cartwheel in combination with a transmitting SAR-satellite［C］//IEEE IGARSS′01.New York：IEEE，2001：2955-2957

［8］V Tollefson M，B K Preiss.Space based radar constellation optimization［C］//IEEE radar conference.New York：IEEE，1998：379-388

［9］G Krieger，A Moreira.Multistatic SAR satellite formations：potentials and challenges［C］//IEEE IGARSS′05.New York：IEEE，2005：2680-2684

［10］H Eiedler，G Krieger，E Jochim，et al.Analysis of bistatic configurations for spaceborne SAR interferometry［C］//EUSAR2002.New York：IEEE，2002：311-315

［11］Moccia A，G Rufino.Space borne along-track SAR interferometry：performance analysis and mission scenarios［J］.IEEE Trans on AES，2001.37（1）：199-213

［12］A Moreira，G Krieger，I Hajnsek，et al.TanDEM-X：a TanDEM-X add-on satellite for single-pass SAR interferometry［C］//IEEE IGARSS′04.New York：IEEE，2004：1000-1003

［13］D Massonnet.The interferometric Cartwheel：a constellation of passive satellites to produce radar images to be coherently combined［J］.INT.J.Remote Sensing，2001，22（12）：2413-2430

［14］E E Stockburger，D N Held.Interferometric moving ground target imaging［C］//IEEE international radar conference.New York：IEEE，1995：438-443

［15］C H Gierull.Ground moving target parameter estimation for two-channel SAR［J］.IEEE Pro.Radar Sonar Navig，2006，153（3）：224-233

［16］C E Livingstone，I Sikaneta，C H Gierull，et al.An airborne synthetic aperture radar（SAR）experiment to support RADARSAT-2 ground moving target indication（GMTI）［J］.Can.J.Remote sensing，2002，28（6）：794-813

［17］A O Kohlhase，R Kroes，S D Amico.Interferometric baseline performance estimations for multistatic synthetic aperture radar configurations derived from GRACE GPS observation［J］.Journal of Geodesy，2006：28-39

［18］T L Hacker，R J Sedwick.Space-based GMTI radar using separated spacecraft interferometry［R］.Cambridge：MIT Space Systems Laboratory，1999

［19］Sikaneta I，C Gierull.Parameter estimation for the phase statistics in interferometric SAR［C］//IEEE International Geoscience and Remote Sensing Symposium.New York：IEEE，2002：1735-1737

［20］H Gierll C.Statistical analysis of multilook SAR interferograms for CEAR detection of ground moving targets［J］.IEEE Trans on GRS，2004，42（4）：691-701

（编辑：张小琳）

Analysis of Moving Target Indication Based on Distributed Space Radar

LI Yan ZHANG Qingjun LIU Yadong LIU Jiuli
（Beijing Institute of Spacecraft System Engineering，Beijing 100094，China）

Eor distributed space radars，the difficuly is clutter suppression during detecting moving targets.This article analyses the effects on detecting performace of along track base line length，ground gradient，pointiing error of beam，and so on.The results provide a reference for satellite formation optimization and design of radar parameter for moving target detection.

space radar；formation configuration；clutter suppression；moving target indication（MTI）

TN959.74

A DOI：10.3969/j.issn.1673-8748.2015.03.011

2014-04-08；

2015-05-12

国家重大科技专项工程

李延，男，博士，研究员，从事微波遥感卫星总体设计工作。Email：gf3liyan@163.com。