敏捷卫星姿态对像移速度与偏流角的影响

黄敏 葛玉君 杨芳 黄群东

（航天东方红卫星有限公司，北京 100094）

敏捷卫星姿态对像移速度与偏流角的影响

黄敏 葛玉君 杨芳 黄群东

（航天东方红卫星有限公司，北京 100094）

针对敏捷卫星需要具备在复杂姿态下推扫成像的能力，建立了卫星在不同姿态下的像移速度和偏流角的数学模型，并进行了仿真分析，讨论了姿态改变对卫星成像带来的影响。仿真分析表明：姿态改变是影响像移速度和偏流角的最大因素，敏捷卫星从一个姿态变化到另一个姿态成像时，需要根据预期的姿态调整相机的积分时间以满足成像质量要求，同时偏流角也需要做相应调整以补偿姿态改变带来的偏流角变化。

像移速度；偏流角；积分时间；敏捷卫星；姿态控制

1 引言

许多先进的小卫星已经具备了快速姿态机动与稳定的敏捷能力，可以实现快速滚动成像、同轨多条带成像、同轨立体成像等，从而提高卫星对地观测的时间分辨率、扩大其观测区域并使其兼具侦察与测绘的能力［1-2］。敏捷卫星快速姿态机动以改变成像姿态，将使得像面的空间方位发生变化，像移速度与偏流角也将随着改变。根据TDI CCD成像原理，推扫方向应当与目标点的像移方向一致，像移速度大小必须与CCD相机的电荷行转移速度相匹配［3-4］，否则成像的调制传递函数（MTE）将下降，图像变得模糊［5］。高分辨率对地观测卫星对像移的要求则更高，需要对敏捷卫星不同姿态下的像移速度与偏流角进行分析。

目前，卫星姿态对像移速度与偏流角的影响分析主要有两种方法：一种是在物面上的计算，采用复杂的球面三角几何和速度合成进行计算［6-9］，不同卫星姿态下需要建立多个模型进行计算，并且计算的是目标点所在物面的像移速度和偏流角，难以满足真实像面像移的分析需要；另一种是在像面上的计算，即在相机坐标系下计算目标点相对于像面的像移速度和偏流角，给出像面上的像移速度和偏流角，更加符合TDI CCD的成像原理。第二种方法中，文献［10］提出了星下点成像的像移速度矢量计算模型，是像移速度和偏流角分析的基本方法；文献［11］给出了俯仰成像和滚动成像像移速度与偏流角计算方法，但是没有对姿态改变造成的影响进行分析，也没有讨论滚动角和俯仰角同时存在时的成像；文献［12］对滚动成像时不同滚动角的情况进行了仿真分析，讨论了滚动角的影响；文献［13］根据滚动角对成像的影响按照滚动角的变化对积分时间进行了分档，并给出了分档后的MTE。上述文献的论述中缺乏卫星姿态改变对像移速度与偏流角的影响分析，尤其是滚动角和俯仰角同时存在时产生的影响尚未有讨论分析，敏捷卫星姿态改变对成像的具体影响也需更加深入的分析。

本文针对以上的问题，首先建立了计算敏捷卫星的像移速度和偏流角的数学模型，在仿真分析的基础上讨论卫星姿态对像移速度与偏流角的影响，进一步分析了敏捷卫星成像的相机积分时间调整及偏流角补偿问题。

2 像移速度与偏流角计算数学模型

敏捷卫星通过姿态快速机动来改变成像姿态以实现对多目标的观测，成像时卫星姿态均保持稳定。根据TDI CCD成像的原理，可以建立如图1中成像几何模型：卫星运行在轨道高度为H的轨道上，卫星的轨道坐标为S-XYZ，坐标原点S为卫星质心，Z轴指向地心，X轴指向飞行方向，Y轴由右手定则确定，星下点为O；卫星的本体坐标系初始时与轨道坐标系重合，当有姿态机动时本体坐标系为由轨道坐标系先绕X轴转动φ角（滚动角），再绕本体Y轴转动θ角（俯仰角）得到，本文假设本体坐标系与相机坐标系重合，成像推扫条带如图1中所示。图中T点是仅有滚动角φ时光轴与地面的交点，卫星质心S到目标点D的矢量为L，地心Oe指向目标点的矢量为Re，α为卫星的下视角。va为地球自转导致的目标点D的绝对速度矢量，ve为卫星运动导致的牵连速度矢量。

图1 成像几何模型Eig.1 Imaging geometric model

目标点D相对于相机坐标系的运动速度矢量vr即为像移速度矢量，由于相对速度等于绝对速度减去牵连速度，得

式中：va=ωe×Re，ωe为地球自转角速度矢量；ve=ωs×Re，ωs为卫星沿轨道运行的角速度矢量。

基于像方的计算方法是将式（1）中所有速度矢量都表示在相机坐标系中，在相机坐标系下计算像移速度，可得像移速度矢量vr在相机坐标系中的三轴分量计算公式：

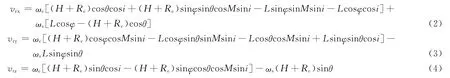
式中：vrx为沿垂直线阵方向像移速度（沿相机坐标系X轴）；vry为沿线阵方向像移速度速度（沿相机坐标系Y轴）；vrz为沿相机坐标系Z轴的分量；i为卫星轨道倾角；M为卫星的纬度幅角；卫星到目标点D的距离下视角α=arccos（cosθcosφ）。

假设相机的焦距为f，像面上的像移速度v1为

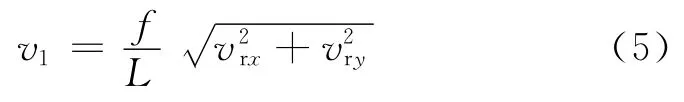
假设像元的大小为d，单个像元的积分时间为

偏流角指在相机坐标系下，像移速度方向与垂直TDI CCD线阵方向的夹角，未做偏航调整时，偏流角η的计算公式［10，14］为

3 仿真分析

根据式（2）和式（3），沿相机坐标系X轴和Y轴的像移分速度与卫星的位置参数和姿态参数相关。本节根据上述计算方法，在同一轨道参数下，对滚动成像、俯仰成像、滚动和俯仰成像的像移速度和偏流角进行仿真分析。TDICCD遥感卫星一般采用太阳同步轨道，因此可取仿真参数如下：轨道高度H为 700 km，地球半径（Re）为6371 km，轨道倾角i为98.193°，相机焦距f为10 m，像元大小d为10μm，卫星的纬度幅角M=0时卫星处于升轨段地球赤道上空。

3.1 像移速度仿真分析

不同姿态下像移速度随卫星纬度幅角M的变化如图2所示，可知：相比于卫星纬度幅角带来的影响，姿态改变会引起像移速度的较大改变。星下点成像时像移速度为0.097 7 m/s，俯仰30°成像时像移速度为0.069 1 m/s，滚动30°成像时像移速度为0.082 7 m/s，滚动角俯仰角均为30°时像移速度为0.058 1 m/s；当卫星姿态保持不变时，卫星运行一圈，像移速度随卫星纬度幅角M的改变在10-3m/s的量级，一景成像中造成的MTE下降可以忽略。

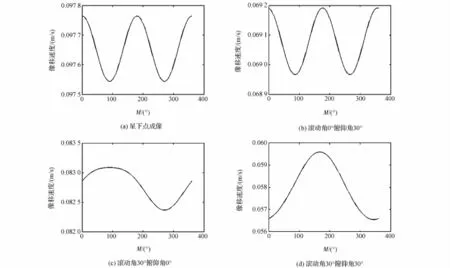
图2 不同姿态下像移速度的变化Eig.2 Image motion velocity in different satellite attitude

敏捷卫星根据成像任务的不同，在同一位置可能有多种姿态，图3为卫星在赤道上空即M=0时，滚动角和俯仰角在30°范围内的像移速度随姿态变化图。可知像移速度在0.055 1 m/s到0.098 2 m/s之间，最大值出现在星下点成像时，最小值出现在俯仰30°滚动30°成像，俯仰角或者滚动角越大时像移速度越小。

有姿态角时，像移速度会有不同程度的下降，这是因为有滚动角时，由于滚动角越大使得卫星到目标点的距离越大，由式（5）可知速高比减小，像移速度减小；有俯仰角时，随着俯仰角度的增大，卫星到目标点的距离变大，同时卫星运动引起的地面牵连速度与像平面有一个夹角，牵连速度投影到像面上使得像移速度减小。因此，姿态改变后卫星到目标点距离的改变以及目标点所在的地平面与像平面的夹角变化是引起像移速度变化的主要原因。

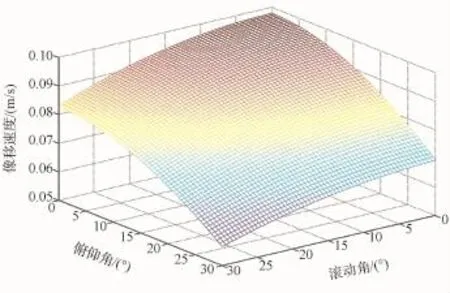
图3 敏捷成像的像移速度Eig.3 Image motion velocity for agile satellite

3.2 偏流角仿真分析

仅有滚动角或俯仰角时偏流角随卫星位置M的变化如图4，其中正负值表示偏流角的方向，可知：星下点成像时，偏流角最大值为3.85°，最小值为-3.85°，随着幅角M的变化而变化。仅有俯仰角时，偏流角的幅值变大，这主要因为俯仰角的存在使得卫星运动引起的牵连速度在像面上的投影随俯仰角变大而变小，即vrx变小，根据式（7），可知偏流角变大，30°俯仰角时偏流角最大为4.81°。仅有滚动角时，偏流角的幅值减小，30°滚动时最大偏流角为3.02°。这是因为随着滚动角变大，像平面与地平面的夹角变大，地球自转的地速投影在本体Y轴上越小，而轨道运动投影在X轴上的速度不变，因此偏流角变小。

图4 仅有滚动角或俯仰角的偏流角变化Eig.4 Drift angle when the pitch roll or yaw angle exists only

图5为滚动角与俯仰角都存在时的偏流角随幅角M的变化图，可知：沿着卫星运动方向，左前、左后、右前、右后方的4个区域，偏流角的变化不相同，需要区别对待。与图4不同，滚动和俯仰的同时存在使得偏流角的最大值与最小值的绝对值不相等，例如滚动30°俯仰30°时的最大值与最小值分别为6.34°和-1.24°。这是由于滚动和俯仰同时存在时，卫星运动造成的牵连速度在像面上的投影关系改变造成的。如图6所示，X轴沿推扫方向，观察某一目标点时，如没有俯仰角和滚转角，卫星运动引起的牵连速度ve在像面的投影沿X轴；当有滚动角时，相当于像面绕X轴转动φ角，此时ve在像面的投影在X与Z′轴上有分量，Y′轴上仍没有分量；当加入俯仰角时，相当于像面再绕Y′轴转动θ角，此时ve在像面上的投影不再沿X＂轴，在Y′轴上的分量出现，从而导致偏流角的变化，从式（3）可以看出，当俯仰角和滚转角同时不为0时，将使得含ωs项不为零，存在耦合作用。

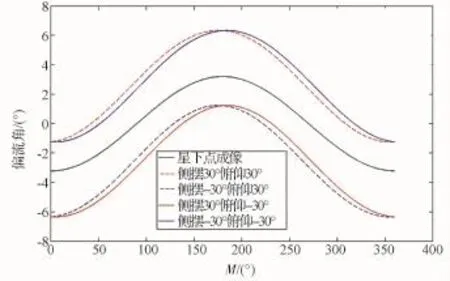
图5 敏捷成像的偏流角变化Eig.5 Drift angle for agile satellite

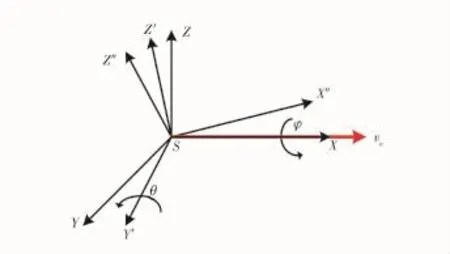
图6 ve在像面的投影关系Eig.6 Projection of veon image plane

4 敏捷卫星成像分析

4.1 TDI CCD积分时间调整

由上述仿真可知，在给定的姿态条件下完成一景成像时像移速度改变不大，TDI CCD的积分时间可以设定为某一恒定的值。当敏捷卫星通过姿态机动以改变成像状态时，例如滚动角和俯仰角均在0°～30°内变化时，像移速度的变化范围在0.055 1～0.098 2 m/s之间。根据式（6）可得积分时间在100～180μs内变化。像移速度的改变直接影响卫星成像质量，通过调整TDI CCD积分时间来实现像移速度与电荷行转移速度相匹配。因此，要实现敏捷卫星在各种复杂姿态下的成像，相机需要可以调节的积分时间，在某一给定姿态下需采用相应的积分时间。相机的积分时间不是连续可调的，可以根据需要设计成不同的分挡，成像时根据相应卫星姿态加以选取。在本文的仿真参数下，表1将敏捷卫星的积分时间划分为17挡以满足12级TDI CCD成像MTE下降不超过2%的要求。图7给出了对积分时间分挡调整后的成像MTE，12级TDI CCD能够满足成像要求，增加TDI CCD级数到24级时MTE下降最大达到了9%，不满足成像要求，此时需要更加细致的积分时间划分。

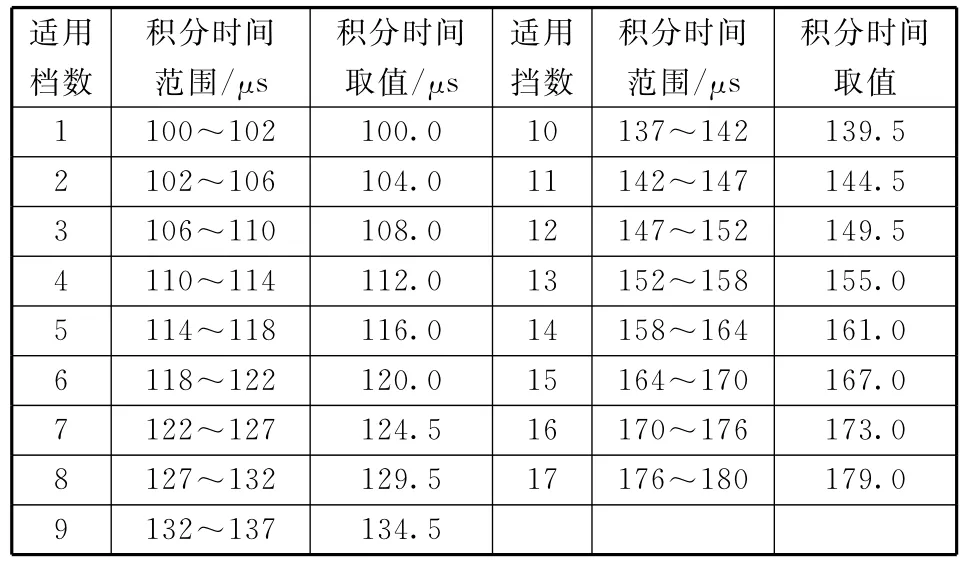
表1 积分时间分挡方案Table 1 Subsection of integration time

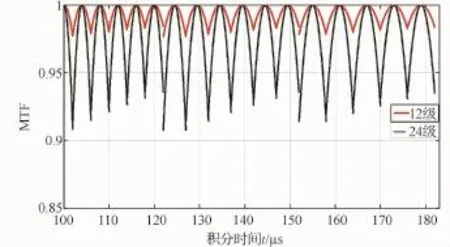
图7 积分时间调整后的MTEEig.7 MTE when the integration time was adjusted

4.2 偏流角补偿

偏流角的控制策略为：根据成像的总体指标得到速度匹配残差的取值范围，从而获得允许的偏流角误差，当偏流角变化量大于允许的偏流角误差时，进行姿态的偏航控制。敏捷成像时，不同姿态下偏流角有较大的改变，例如图5中卫星在M=180°时从滚动30°俯仰30°姿态改变成滚动30°俯仰-30°姿态时，偏流角从6.34°改变成1.21°，卫星姿态快速机动过程中除了绕滚动轴和俯仰轴做快速姿态机动外，偏航轴也需要进行姿态调整。此外，大角度成像时，例如俯仰30°滚动30°成像时最大偏流角可达6.34°，比星下点成像的最大偏流角（3.85°）大2.49°。

5 结束语

本文对不同姿态下的像移速度及偏流角进行了研究，分析了敏捷卫星成像的相机积分时间调整和偏流角补偿问题。下视角30°范围内成像时，像移速度在0.055 1～0.098 2 m/s之间变化，因此姿态改变是引起像面像移速度改变的主要因素，为满足不同姿态下的成像，敏捷卫星相机需要根据成像要求来设计积分时间分挡，在相应姿态下选择相应的积分时间进行成像。姿态改变将引起偏流角最大约5.13°的变化，卫星偏流角控制时需要做出快速响应以适应新的成像姿态。本文对不同姿态下成像的像移速度与偏流角的分析，可以为敏捷卫星在复杂姿态下的成像提供参考。

（

）

［1］Jean J，Eric J，Gerard L，et al.Attitude guidance technics developed in CNES for earth observation and scientific missions［C］//The 28thannual AAS Guidance and control Conference Breckenridge.San Diego，CA：AAS，2005：11-16

［2］郝会成，姜维，李一军，等.基于Multi-Agent敏捷卫星动态任务规划问题［J］.国防科技大学学报，2013，35（1）：53-59 Hao Huicheng，Jiang Wei，Li Yijun，et al.Research on agile satellite dynamic mission planning based on multiagent［J］.Journal of National University of Defense Technology，2013，35（1）：53-59（in Chinese）

［3］于涛，徐抒岩，韩诚山，等.空间相机偏流角的间歇式实时调整［J］.光学精密工程，2009，17（8）：1908-1914 Yu Tao，Xu Suyan，Han Chenshan，et al.Batch-type real-time adjustment for drift angle of space camera［J］.Optics and Precision Engineering，2009，17（8）：1908-1914（in Chinese）

［4］黄群东，杨芳，赵健.姿态对地指向不断变化成像时的偏流角分析［J］.宇航学报，2012，33（10）：1544-1551 Huang Qundong，Yang Eang，Zhao Jian.Drift angle analysis for agile satellite imaging when its attitude points to the earth changing continuously［J］.Journal ofAstronautics，2012，33（10）：1544-1551（in Chinese）

［5］杨秀彬，贺小军，张刘.偏流角误差对TDI CCD相机成像的影响与仿真［J］.光电工程，2008，35（11）：45-50 Yang Xiubin，He Xiaojun，Zhang Liu.Effect and simulation of the deviant angle error on TDI CCD cameras image［J］.Opto-Electronic Engineering，2008，35（11）：45-50（in Chinese）

［6］景泉.敏捷卫星偏流角计算模型研究［J］.航天器工程，2012，21（4）：16-20 Jing Quan.Research on computation model of bias angle for agile satellite［J］.Spacecraft Engineering，2012，21（4）：16-20（in Chinese）

［7］袁孝康.星载TDICCD推扫相机的偏流角计算与补偿［J］.上海航天，2006，23（6）：10-13.Yuan Xiaokang.Calculation and compensation for the deviant angle of satellite borne TDI-CCD push scan camera［J］.Aerospace Shanghai，2006，23（6）：10-13（in Chinese）

［8］樊超，梁义涛，李伟，等.偏流角对空间相机影响研究［J］.电光与控制，2008，15（11）：76-79 Ean Chao，Lang Yitao，Li Wei，et al.Study on influence of drift angle on the space camera［J］.Electronics Optics &Control，2008，15（11）：76-79（in Chinese）

［9］王志刚.高分辨率卫星遥感图像的偏流角及其补偿研究［J］.宇航学报，2002，23（5）：39-42 Wang Zhigang.Study on satellite remote sensing high resolution image bias angle and its compensation［J］.Journal of Astronautics，2002，23（5）：39-42（in Chinese）

［10］王家骐，于平，颜昌翔，等.航天光学遥感器像移速度矢计算数学模型［J］.光学学报，2004，24（12）：1585-1589 Wang Jiaqi，Yu Ping，Yan Changxiang，et al.Space optical remote sensor image motion velocity vector computational modeling［J］.Acta Optical Sinica，2004，24（12）：1585-1589（in Chinese）

［11］陈绍龙.侧摆摄影偏流角和速高比的计算模型［J］.航天器工程，2010，19（1）：36-40 Chen Shaolong.Computation model of veer angle and velocity height ratio for space camera in roll attitude［J］.Spacecraft Engineering，2010，19（1）：36-40（in Chinese）

［12］黄群东，杨芳，赵健.姿态对地指向不断变化成像时的像移速度计算［J］.光学精密工程，2012，20（12）：2812-2820 Huang Qundong，Yang Eang，Zhao Jian.Calculation of image motion velocity for agile satellite dynamic imaging to changed continuously attitude point［J］.Optics and Precision Engineering，2012，20（12）：2812-2820（in Chinese）

［13］胡永力，谭南征.TDICCD相机侧摆MTE的研究［J］.航天返回与遥感，2003，24（1）：33-37 Hu Yongli，Tan Nanzheng.Study on scroll MTE of TDICCD camera［J］.Spacecraft Recovery&Remote Sensing，2003，24（1）：33-37（in Chinese）

［14］李友一.空间相机中的偏流角控制［J］.光学精密工程，2002，10（4）：402-406 Li Youyi.Study of the drift angle control in a space camera［J］.Optics and Precision Engineering，2002，10（4）：402-406（in Chinese）

（编辑：张小琳）

Analysis on Image Motion Velocity and Drift Angle for Agile Satellite

HUANG Min GE Yujun YANG Eang HUANG Qundong
（DEH Satellite Co.Ltd.，Beijing 100094，China）

The agile satellite needs to have the capability to realize push-broom imaging in complex satellite attitude condition.In this paper，a mathematic model to calculate the image motion velocity and the drift angle of agile satellite is built，and the image motion velocity and the drift angle in different attitudes are simulated in order to analyze their influence on image acquisition.The simulation and analysis show that the various satellite attitudes affect the image motion velocity and the drift angle most.When the agile satellite changes its attitude from one to another，according to the expected attitude，its camera should adjust its integration time to attain high imaging quality，and at the same time，the yaw angle should be controlled to compensate the change of drift angle caused by the attitude change.

image motion velocity；drift angle；integration time；agile satellite；attitude control

V443.5

A DOI：10.3969/j.issn.1673-8748.2015.03.006

2014-10-09；

2015-04-28

黄敏，男，硕士，研究方向为航天器总体设计。Email：minmin677@163.com。