海上风机斜壁桶形基础承载特性研究

刘金龙，陈陆望，汪东林，王吉利

(1. 合肥学院 建筑工程系, 安徽 合肥 230601; 2. 合肥工业大学 资源与环境工程学院, 安徽 合肥 230009; 3. 安徽建筑大学 土木工程学院, 安徽 合肥 230601; 4. 中国科学院 武汉岩土力学研究所, 湖北 武汉 430071)

海上风机斜壁桶形基础承载特性研究

刘金龙1，陈陆望2，汪东林3，王吉利4

(1. 合肥学院 建筑工程系, 安徽 合肥 230601; 2. 合肥工业大学 资源与环境工程学院, 安徽 合肥 230009; 3. 安徽建筑大学 土木工程学院, 安徽 合肥 230601; 4. 中国科学院 武汉岩土力学研究所, 湖北 武汉 430071)

基于验证的三维有限元方法，考察了斜壁桶形基础的承载特性，得到了变形网格、位移增量分布、位移等值面分布等结果，探讨了斜壁倾角与各极限承载力之间的定量关系。计算表明，桶形基础发生竖向位移时，主要是桶体内部和桶基正下方的土体发生沉降，而桶侧的土体基本不发生沉降。桶形基础受到水平荷载发生转动时，转动中心轴大致位于桶基底面内，桶基水平承载力主要由桶内土体和桶基外侧中上部受压侧土体产生的抵抗反力构成。桶基因受到较大竖直向上荷载而失效时，桶内土体和桶基外侧靠近海床面附近土体产生了较大的向上位移。桶壁倾角β每增加1°，竖向抗压极限承载力、竖向抗拔极限承载力、水平极限承载力分别提高12%、17.4%及3.8%。

斜壁桶形基础; 三维有限元; 竖向抗压极限承载力; 水平极限承载力; 竖向抗拔极限承载力

我国近海风能资源具有巨大的开发潜力，然而由于海洋环境较为恶劣、地质条件异常复杂，导致海上风电工程建设的难度与投资风险大大增加。

目前海上风机基础部分采用重力混凝土和钢桩结构基础[1- 3]。但在浅海区域，由于大型施工船舶无法进入，不具备打桩的施工环境，传统的风电基础形式不再适用，需发展一种更加高效与经济的新型基础形式。

桶形基础就是为适应海洋地质条件而发展起来的一种基础形式，其上部封闭、底部开口，因像倒扣在土中的圆桶而得名，可用于海上风电工程、浅海石油与天然气资源开发、海上浮动式结构物的系泊工程等，被称为“导管架基础工程技术新时代的曙光”[4- 7]。已有多个海洋工程成功使用了直壁式桶形基础[8- 12]。

事实上，为了把应力扩散到更大面积的桶底土层上，可以采用斜壁形式的桶形基础。Zeinoddini M等[13]对斜壁桶形基础的抗拉承载特性进行了研究，并分析了土体黏聚力、内摩擦角、桶基直径、桶壁斜率等对抗拉承载特性的影响。徐文强等[14- 15]对斜壁桶形基础的承载力研究表明，随着桶壁斜率的增加，竖向承载力增加幅度较大，而水平承载力增加幅度相对较小。桶壁倾斜增加了桶基贯入海床的施工难度，故这类基础一般仅适用于土体强度较低、压缩性较大的淤泥与淤泥质土。总体上看，作为一种新型桶基基础，目前对斜壁桶形基础的研究较少，缺乏有效的试验数据，特别是对其竖向抗压、竖向抗拔、水平承载力的综合研究较少。

为此，本文基于三维有限元分析方法，对斜壁桶形基础的竖向抗压承载力、竖向抗拔承载力、水平承载力进行了系统研究，考察了斜壁倾角对各承载力的影响，对比分析了斜壁与直壁桶形基础的承载力差异，为桶形基础的设计与应用提供参考。

1 三维有限元计算模型

1.1计算模型的建立

传统的桶形基础为直壁式，如图1(a)所示。而斜壁式桶形基础是指桶壁向外倾斜某一角度，如图1(b)所示。现拟通过有限元对比计算，考察这两种构型桶基的承载力特性。

基于大型有限元计算软件Plaxis 3D建立斜壁桶形基础的有限元分析模型，如图2所示。为了减小边界条件的影响，计算模型的长、宽、高均大于10倍的桶基高度H。模型采用10节点的三维四面体单元进行网格剖分。桶体一般为钢结构制作可视为线弹性体，弹性模量取E=2.1×108kPa，泊松比取v=0.21。海床土采用莫尔-库仑理想弹塑性模型。桶体与海床土体之间的摩擦通过设置接触面单元来实现。接触面单元采用参数Rinter来反映两者相互作用的程度，Rinter=[0, 1.0]。Rinter的具体取值可通过与试验数据的拟合试算确定。

本文计算中，假定桶基已被施工、安置于海床土体中，施工扰动对海床土体的影响已结束，海床土体已恢复其原始物理力学参数，即暂不考虑施工过程对桶基承载力特性的影响。

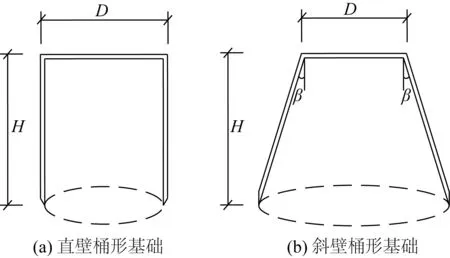
图1 常见桶形基础构型Fig. 1 Typical model of bucket foundation

图2 斜壁桶形基础三维有限元计算模型Fig. 2 3D FEM model of tapered bucket foundation

可采用位移控制法或荷载控制法进行加载。一般地，采用位移控制法能准确得到桶基的荷载- 位移曲线，当荷载- 位移曲线的斜率接近于零时，表明在荷载不变的情况下桶基位移持续增大，据此可认为此时的地基已达到极限状态，与此对应的荷载就是海床地基的极限承载力[15]。当然，采用荷载控制法时，当不同桶基承受相同的荷载时，海床土体发生的位移越小表明该类型的桶基承载力越大。

1.2计算模型的验证

张宏祥[16]对桶形基础开展了大规模试验，分析了桶形基础内外土压力的变化情况以及水平荷载下桶基的变位规律，得到了桶基加载过程中的P-S曲线。试验场地土的参数为[16]：黏聚力c=3 400 Pa，内摩擦角φ=4°，弹性模量E=7.3×105Pa，泊松比v=0.4。模型试验的直壁桶基直径D=300 mm，桶高H=500 mm。

基于上述原理建立有限元计算模型，计算得到竖向抗压结果与张宏祥的实测结果对比，见图3。计算过程中对Rinter的取值进行了大量试算，图3为Rinter=0.4的计算结果。

由图3可见，计算得到的P-S曲线与试验数据曲线较吻合。一般地，可将s=(0.03～0.06)D(D为桶基的直径)对应的荷载值作为承载力特征值。鉴于海床土通常为松散的淤泥质软黏土，不妨按s=0.06D对应的荷载值作为桶基的竖向承载力特征值。基于实验数据曲线得到的竖向承载力特征值为4.03 kPa，有限元计算得到的承载力特征值为4.30 kPa，两者误差为6.7%，其精度可以接受。

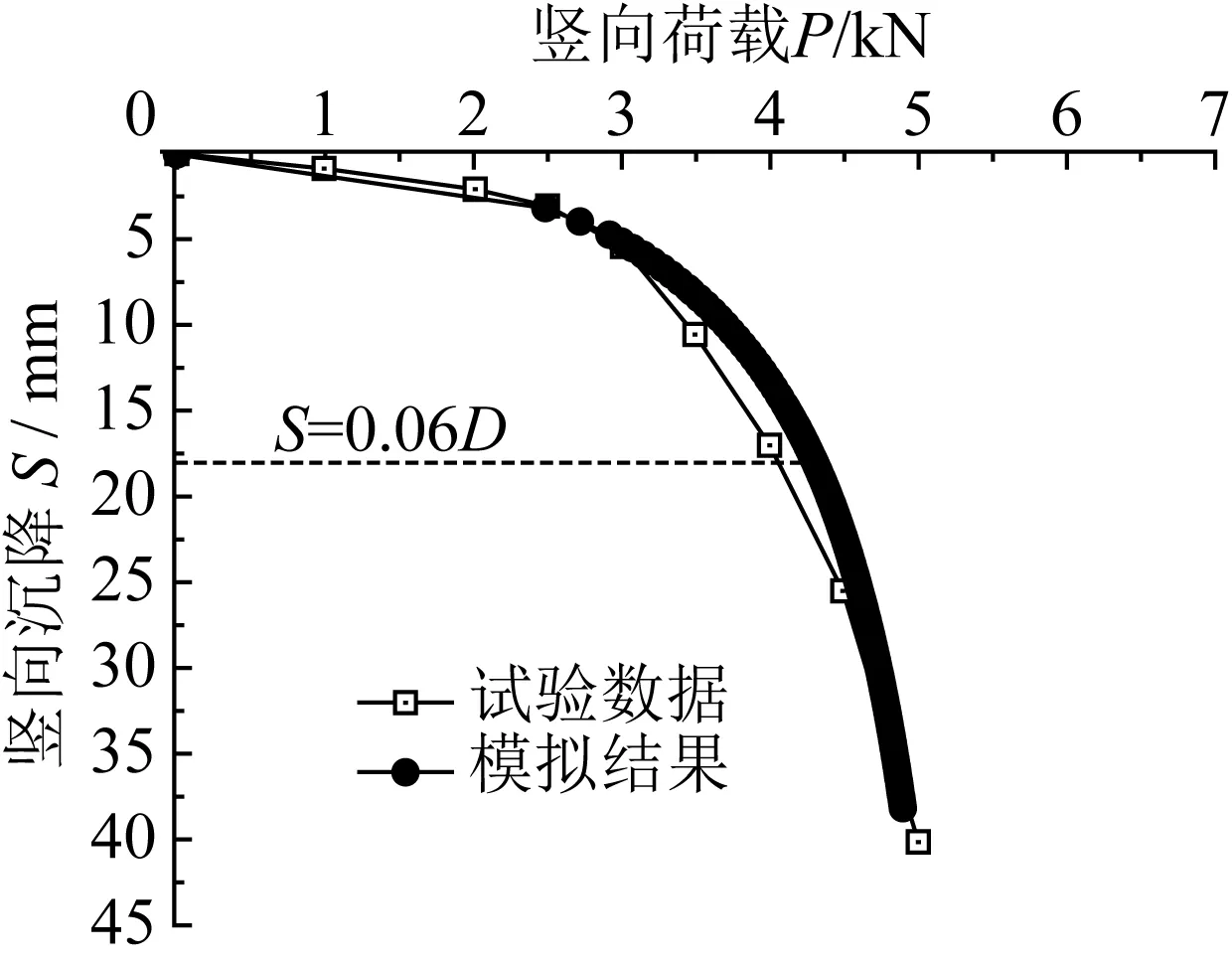
图3 直壁桶基竖向承载力计算值与实测值的对比Fig. 3 Comparison between computed and measured data of vertical bearing capacity of vertical bucket foundation

图4 桶形基础竖向受压变形示意Fig. 4 Deformation of bucket foundation by vertical compressive load

可见，本文建立的有限元计算模型是合理的。鉴于实验数据的有限性，本文假定基于上述有限元模型进行抗拔、水平承载力计算也是可行、有效的。现基于该计算模型开展斜壁桶形基础竖向抗压、竖向抗拔、水平承载力的对比计算。

2 竖向抗压承载力分析

采用位移控制法来确定桶形基础的竖向抗压极限承载力，即在桶基顶部中心施加一个位移值s，通过有限元计算即可得到桶形基础的P-S曲线。该位移值不能过小，通常应大于桶形基础的高度值，本处计算取s=2H(当s值过大时，有限元计算在未达到s值时出现计算不收敛而中断，但其对极限承载力的确定无影响)。

仍采用上述张宏祥模型试验的桶基参数，通过取不同的β值来考察斜壁桶形基础的承载特性。图4给出了桶基受压后的网格变形示意图，图5给出了桶基受压后海床土体的位移增量分布情况。

综合分析图4与图5可知，桶形基础发生竖向位移时，主要是桶体内部和桶基正下方的土体发生沉降，而桶侧的土体基本不发生沉降。桶体内部和桶基正下方的土体发生沉降，实际上是桶体内部土体进一步被压缩、挤密的过程。桶基沉降越大桶体内部的土体被挤压越密实，其产生的抵抗力也越大，这就是竖向承载力的形成过程。

图5 桶基竖向受压后土体位移增量分布 Fig. 5 Displacement increment of soil when vertical compressive load acts on bucket foundation

图6 桶基受竖向抗压荷载失效时土体位移为3 cm的等值面Fig. 6 Contour plane of 3 cm of soil displacement when vertical compressive load acts on bucket foundation

桶形基础受到竖向抗压荷载而达到极限状态时，海床地基土体内位移为3 cm的等值面分布如图6所示。可见，桶壁倾斜时，其相同位移的等值面明显比直壁桶形基础的要大。即斜壁桶形基础有更大、更多的土体来支撑、承担上部桶体位移，故其承载力更大。

为了进一步说明图6所反映的现象，不妨采用荷载控制法对桶基的位移进行考察。在桶基顶部中心施加竖向荷载4.0 kN，得到直壁与斜壁桶形基础土体中位移为5 mm的等值线分布情况，见图7。

由图7可见，承受相同竖向荷载时，斜壁桶形基础内相同位移的土体体积明显比直壁桶形基础小得多。即对于斜壁桶形基础，只需依靠体积较少的海床土体就能承受竖向荷载4.0 kN，而直壁桶形基础需要较大、较多的海床土体共同发挥作用才能承担该竖向荷载。

图7 竖向荷载为4.0 kN时土体位移为5 mm的等值线Fig. 7 Contour of 5 mm of soil displacement when vertical compressive load 4.0 kN act on bucket foundation

图8 桶壁倾角对竖向抗压极限承载力的影响Fig. 8 Influence of slope angle of bucket wall on ultimate vertical compressive load of bucket foundation

土体发生位移是土体受到附加应力后的宏观表现，土体位移越小表明该处的附加应力越小。从图7可以发现，对于相同的竖向荷载，斜壁桶形基础下方某点(任意点)处的土体位移比直壁桶形基础情况下的土体位移要小，即相同位置处斜壁桶形基础产生的附加应力更小。若以相同位移(如s=0.06D)对应的荷载值作为桶基的承载力特征值，显然斜壁桶形基础的承载力特征值更大。

基于位移控制法，计算得到了不同桶壁倾角β值对应的竖向抗压极限承载力Fvc(Vertical Compress)，如图8所示。可见，竖向抗压极限承载力随着桶壁倾角的增大而近似线性增大。

直壁桶形基础(β=0°)的竖向抗压极限承载力为4.89 kN，而β=8°时的竖向抗压极限承载力为9.44 kN，约为直壁桶形基础的2倍。桶壁倾角β每增加1°，桶基竖向抗压极限承载力约提高12%。可见，桶壁的倾斜对提高竖向抗压承载力有明显的效果。认识到这一点，对桶形基础的优化设计有重要的促进作用。

3 水平承载力分析

一般地，海上风机承受较大的水平风力荷载，其迫使风机叶轮转动而产生电能。特别是遇到罕见台风时，桶基有可能因受到较大的水平荷载而发生倾覆破坏。

图9给出了桶基受到水平荷载后的网格变形情况，图10给出了桶基受水平荷载后海床土体的位移增量分布情况。

图9 桶形基础受水平荷载变形示意Fig. 9 Deformation of bucket foundation by horizontal load

图10 桶基受水平荷载后土体位移增量分布Fig. 10 Displacement increment of soil when horizontal load acts on bucket foundation

综合分析图9与图10可知，桶形基础受到水平荷载时发生转动，转动中心轴大致位于桶基底面内。桶基因受到较大水平荷载发生转动、失效时，桶内土体和桶基外侧中上部受压侧土体产生了较大的位移，而其它部位(如桶基底部、桶基外侧受拉侧)的土体产生的位移较小。可见，桶基水平承载力主要由桶内土体和桶基外侧中上部受压侧土体产生的抵抗反力构成。

桶形基础受到水平荷载而达到极限状态时，海床地基土体内位移为2 cm的等值面分布如图11所示。可见，桶壁倾斜时，其相同位移的等值面比直壁桶形基础的要大。即斜壁桶形基础有更大更多的土体来支撑、承担桶体的水平位移，故其水平承载力更大。

为了进一步说明图11所反映的现象，采用荷载控制法对桶基的位移进行考察。在桶基顶部中心施加水平荷载1.0 kN，得到直壁与斜壁桶形基础地基土体中位移为2 mm的等值线分布情况，见图12。

图11 桶基受水平荷载失效时土体位移为2 cm的等值面Fig. 11 Contour plane of 2 cm of soil displacement when horizontal load acts on bucket foundation

图12 水平荷载为1.0 kN时土体位移为2 mm的等值面对比Fig. 12 Contour of 2 mm of soil displacement when horizontal load 1.0 kN acts on bucket foundation

图13 桶壁倾角对水平极限承载力的影响Fig. 13 Influence of slope angle of bucket wall on ultimate horizontal load of bucket foundation

由图12可见，承受相同的水平荷载时，斜壁桶形基础内相同位移的土体体积比直壁桶形基础的要小。即对于斜壁桶形基础，只需依靠体积较少的海床土体就能承受水平荷载1.0 kN，而直壁桶形基础需要较大、较多的海床土体共同发挥作用才能承受该水平荷载。因此斜壁桶形基础的水平承载力更高。

基于位移控制法，计算得到了不同桶壁倾角β值对应的水平极限承载力FH(Horizontal)，如图13所示。可见，水平极限承载力随着桶壁倾角的增大而近似线性增大。

直壁桶形基础(β=0°)的水平极限承载力为1.46 kN，β=6°时的水平极限承载力为1.79 kN。桶壁倾角β每增加1°，桶基水平极限承载力约提高3.8%。可见，桶壁的倾斜对提高水平承载力有一定的作用，但小于提高竖向抗压承载力的效果。

4 竖向抗拔承载力分析

图14 桶形基础受竖直向上荷载后变形示意Fig. 14 Deformation of bucket foundation by vertical uplift load

单桶基础受到较大的水平荷载时，一般表现为一侧受拉而另一侧受压。当多桶基础组成的海洋平台受到较大水平荷载时，可能表现出某个或某些桶基受到竖直向上的拉力，而其它桶基受到竖直向下的压力。可见，桶形基础经常受到较大的竖直向上拉力(即上拔力)，因此有必要探讨桶形基础的竖向抗拔承载力。

图14给出了桶基受到竖直向上荷载后的变形示意，图15给出了β=6°时的桶基受竖直向上荷载后海床土体与桶基之间的网格变形情况。可见，桶基受到的竖向拔力超过桶侧与土体摩擦力和桶内土体抗力之和时，桶基发生过大向上位移而导致失效。

图16给出了桶基受竖直向上荷载后海床土体的位移增量分布情况。可见，桶基因受到较大竖直向上荷载而发生失效时，桶内土体和桶基外侧靠近海床面附近土体产生了较大的向上位移，而其它部位(如桶基底部、远离桶基外侧部位)的土体产生的位移较小。因此，桶基竖向抗拔承载力主要由桶基外侧与土体的摩擦力和桶内土体抗力构成。

图15 β=6°时桶基受竖直向上荷载后网格变形情况(放大5倍)Fig.15 Mesh deformation of bucket foundation by vertical uplift load when β=6°(5 times magnified)

图16 桶基受竖直向上荷载后土体位移增量分布Fig. 16 Displacement increment of soil when vertical uplift load act on bucket foundation

一般桶基施工就位后，要求桶内土体与桶内壁完全接触、无空隙，且负压沉贯要求桶体处于密封状态。因此，当桶基受到较大上拔力而与桶内土体发生分离趋势时，桶内土体与桶基内腔之间不太可能形成真空，也不太可能形成空腔由空气来填充(海面以下的海床土体中的空气体积非常有限，可以忽略不计)。桶基与桶内土体发生分离趋势时，可能存在的是：① 桶内土体与桶基内腔之间产生的空腔由水填充，② 桶内土体与桶基内腔之间不发生相对位移而不形成空腔，即桶内土体与桶基一起同步产生向上位移。

而水能否由渗透作用进入桶内土体与桶基内腔之间的空腔，取决于海床土体的渗透性与抗拔作用时间。当海床土体渗透系数较小且桶基高度较大嵌入海床土体较深时，水也难以进入桶基内腔，此时桶内土体只能与桶基同步产生向上位移。由于本文计算不考虑渗流的作用与影响，故图16反映的是桶内土体与桶基同步产生向上位移的情况。

因受到上拔力而导致桶内土体与桶基同步产生向上位移时，土体的抗力一部分由其重力组成，另一部分来自土体的抗拔承载力。另外，桶基外侧与海床土体之间的摩擦力也会阻止桶基的向上移动。特别地，当桶壁倾斜时，桶壁与土体之间的接触力更大，从而使桶基外侧与海床土体之间的摩擦力也更大。

图17 桶壁倾角对竖向抗拔极限承载力的影响Fig. 17 Influence of slope angle of bucket wall on limited vertical uplift load of bucket foundation

基于位移控制法，计算得到了不同桶壁倾角β值对应的竖向抗拔极限承载力Fvu(Vertical Uplift)，如图17所示。可见，竖向抗拔极限承载力随着桶壁倾角的增大而近似线性增大。

直壁桶形基础(β=0°)的竖向抗拔极限承载力为1.17 kN，β=4°时的竖向抗拔极限承载力为2.03 kN。桶壁倾角β每增加1°，桶基竖向抗拔极限承载力约提高17.4%。可见，桶壁的倾斜对提高竖向抗拔承载力有较大的作用，大于提高竖向抗压承载力与水平承载力的效果。

鉴于问题的复杂性以及桶形基础的特殊性，本文上述研究成果还有待结合模型试验进行深入验证。或者说，模型试验可以在本文数值研究成果的基础上更好地设计与开展。

5 结 语

1) 桶形基础发生竖向位移时，主要是桶体内部和桶基正下方的土体发生沉降，而桶侧的土体基本不发生沉降。竖向抗压极限承载力随着桶壁倾角的增大而近似线性增大，桶壁倾角β每增加1°，桶基竖向抗压极限承载力约提高12%。

2) 桶形基础受到水平荷载时发生转动，转动中心轴大致位于桶基底面内。桶基水平承载力主要由桶内土体和桶基外侧中上部受压侧土体产生的抵抗反力构成。水平极限承载力随着桶壁倾角的增大而近似线性增大，桶壁倾角β每增加1°，桶基水平极限承载力约提高3.8%。

3) 桶基因受到较大竖直向上荷载而发生失效时，桶内土体和桶基外侧靠近海床面附近土体产生了较大的向上位移，而其它部位土体产生的位移较小。竖向抗拔极限承载力随着桶壁倾角的增大而近似线性增大，桶壁倾角β每增加1°，桶基竖向抗拔极限承载力约提高17.4%。

[1] 刘悦, 时志刚, 胡颖, 等. 海上风电技术特性对比分析[J]. 船舶工程, 2012, 34(1): 95- 99. (LIU Yue, SHI Zhigang, HU Ying, et al. Analysis on characteristic of offshore wind technology[J]. Ship Engineering, 2012, 34(1): 95- 99. (in Chinese))

[2] 黄维平, 李兵兵. 海上风电场基础结构设计综述[J]. 海洋工程, 2012, 30(2): 150- 156. (HUANG Weiping, LI Bingbing. Reviews and comments on the design for offshore wind structures[J]. The Ocean Engineering, 2012, 30(2): 150- 156. (in Chinese))

[3] 孙文, 刘超, 张平, 等. 国内外海上风电机组基础结构设计标准浅析[J]. 海洋工程, 2014, 32(6): 128- 136. (SUN Wen, LIU Chao, ZHANG Ping, et al. Reviews and comments on the design standards for offshore wind structures[J]. The Ocean Engineering, 2014, 32(6): 128- 136. (in Chinese))

[4] ISKANDER M, EI- GHARBAWY S. Performance of suction caissons in sand and clay[J]. Can Geotech, 2002, 39: 576- 584.

[5] LUKE A M, RAUCH R F, OLSON R E, et al. Components of suction caisson capacity measured in axial pullout tests[J]. Ocean Eng., 2005, 32(7): 878- 891.

[6] SAK M, HESHAM El- Naggar M. Centrifuge modeling of tapered piles in sand[J]. Geotechnical Testing Journal, 2003, 26(1):22- 35.

[7] ZIL'BERBERG S D, SHERSTNEV A D. Construction of compaction tapered pile foundations (from the experience of the Valdespetsstroi Trust)[J]. Soil Mechanics and Foundation Engineering, 1990, 27(3): 96- 101.

[8] ZDRAVKOVIC L, POTTS D M, JARDINE R J. A parametric study of the pull- out capacity of bucket foundations in soft clay[J]. Geotechnique, 2001, 51(1): 55- 67.

[9] AUBENY C P, HAN S W, MURFF J D. Inclined load capacity of suction caissons[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2003, 27(14): 1235- 1254.

[10] HOULSBY G T, BYRNE B W. Design procedures for installation of suction caissons in sand[J]. Geotechnical Engineering, 2005, 158(GE3): 135- 144.

[11] 王庚荪, 孔令伟, 杨家岭, 等. 水平载荷作用下土体与桶形基础的相互作用[J]. 工程力学, 2004, 21(2): 107- 113. (WANG Gengsun, KONG Lingwei, YANG Jialing, et al. Interaction of soil mass and bucket foundation under horizontal loads[J]. Engineering Mechanics, 2004, 21(2): 107- 113. (in Chinese))

[12] 武科, 栾茂田, 范庆来, 等. 复合加载模式下桶形基础破坏包络面弹塑性有限元数值分析[J]. 工程力学, 2008, 25(11): 156- 161. (WU Ke, LUAN Maotian, FAN Qinglai, et al. Numerical analysis of failure envelopes of bucket foundation subjected to combined loads beased on elasto- plastic FEM[J]. Engineering Mechanics, 2008, 25(11): 156- 161. (in Chinese))

[13] ZEINODDINI M, KEYVANI J, NABIPOUR M. Tapered suction caissons: A numerical investigation into their pull- out performance[J]. China Ocean Engineering, 2009, 23(4): 695- 707.

[14] 徐文强, 袁凡凡, 李火兵, 等. 斜壁桶形基础水平承载力的三维有限元分析[J]. 中国科学院研究生院学报, 2012, 29(2): 200- 205. (XU Wenqiang, YUAN Fanfan, LI Huobing, et al. Horizontal bearing capacity of tapered bucked foundations based on three- dimensional finite element numerical analysis[J]. Journal of Graduate University of Chinese Academy of Sciences, 2012, 29(2): 200- 205. (in Chinese))

[15] 徐文强, 袁凡凡, 韦昌富, 等. 斜壁桶形基础承载特性的三维有限元分析[J]. 岩土工程学报, 2011, 33(增刊1): 485- 490. (XU Wenqiang, YUAN Fanfan, WEI Changfu, et al. Bearing capacity of suction tapered bucked foundations based on three- dimensional finite element numerical analysis[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(S1): 485- 490. (in Chinese))

[16] 张宏祥. 软土地基中桶形基础的承载力研究与优化设计[D].吉林大学, 2007. (ZHANG Hongxiang. Study on bearing mechanism and optimization design of bucket foundation soft clay[D]. Jilin University, 2007. (in Chinese))

Bearing capacity of tapered bucket foundation for offshore wind turbine

LIU Jinlong1, CHEN Luwang2, WANG Donglin3, WANG Jili4

(1. Department of Civil Engineering, Hefei University, Hefei 230601, China; 2. School of Resource and Environmental Engineering, Hefei University of Technology, Hefei 230009, China; 3. School of Civil Engineering, Anhui Jianzhu University, Hefei 230601, China; 4. Institute of Rock and Soil Mechanics, Chinese Academy of Sciences, Wuhan 430071, China)

Based on verified three- dimensional FEM, the bearing capacity of tapered bucket foundation for offshore wind turbines has been studied, the deformed mesh, incremental displacement, contour plane of displacement got, and the relationship between slope angle of bucket wall and bearing capacity of tapered bucket foundation revealed. It is found that only soil inside and under bucket foundation would be settled when vertical compressive load acts on bucket foundation, while soil around bucket foundation would not be deformed obviously. Bucket foundation would be rotated with horizontal load, and the rotation center axis is approximately located in the basal plane of bucket foundation. The horizontal bearing capacity of bucket foundation essentially is the resistance of the soil inside and outside compressive upper side around bucket foundation. The soil inside and outside upper side around bucket foundation would get big upward displacement when vertical uplift load acts on bucket foundation. When the slope angle of bucked wallβincreases by 1°, the vertical compressive ultimate bearing capacity, vertical uplift ultimate bearing capacity and horizontal ultimate bearing capacity would be enhanced by 12%, 17.4%, 3.8% respectively.

tapered bucket foundation; three- dimensional FEM; vertical compressive ultimate bearing capacity; horizontal ultimate bearing capacity; vertical uplift ultimate bearing capacity

P754

A

10.16483/j.issn.1005- 9865.2015.05.009

1005- 9865(2015)05- 066- 07

2014- 12- 11

国家自然科学基金资助项目(41306088)；合肥学院土木工程重点建设学科资助项目(2014xk04)；合肥学院学科带头人培养对象资助项目(2014dtr01)

刘金龙(1979- ), 男, 江西宜丰人, 博士, 教授, 主要从事岩土工程教学与研究。 E- mail: alnile@163.com