考虑桩土相互作用的高桩码头体系等效阻尼比及Pushover分析

高树飞，贡金鑫，冯云芬

(1. 大连理工大学 海岸和近海工程国家重点实验室，辽宁 大连 116024； 2. 聊城大学 建筑工程学院， 山东 聊城 252059)

考虑桩土相互作用的高桩码头体系等效阻尼比及Pushover分析

高树飞1，贡金鑫1，冯云芬2

(1. 大连理工大学 海岸和近海工程国家重点实验室，辽宁 大连 116024； 2. 聊城大学 建筑工程学院， 山东 聊城 252059)

为考虑桩土相互作用的高桩码头体系等效阻尼比，将地震作用下高桩码头的滞回耗能定义为各桩塑性铰耗能和桩-土相互作用耗能之和，桩-土相互作用耗能根据p-y曲线和Masing准则定义的滞回环确定，码头结构的塑性铰总耗能为各桩塑性铰耗能的总和，按照正弦激励下一个振动循环内高桩码头体系与相应单自由度体系粘滞耗能相等的原则，推导得到了高桩码头体系等效阻尼比计算公式，并对两个高桩码头进行了Pushover分析。分析表明，土体耗能对高桩码头体系阻尼贡献较大，根据码头各桩塑性铰出现顺序和转动情况计算码头的等效阻尼比更符合实际情况。

高桩码头；抗震设计；等效阻尼比；桩-土相互作用；滞回阻尼；Pushover分析

静力非线性分析(Pushover分析方法)的能力谱法是国外基于位移高桩码头抗震设计标准和指南采用的确定位移的主要方法[1]，如美国《海洋油码头和维护标准》(简称MOTEMS)[2]、《长滩港码头设计标准》(简称POLB)[3]、《洛杉矶港集装箱码头抗震设计、升级和维修规范》(简称POLA)[4]和《顺岸式和突堤式高桩码头抗震设计》(ASCE/COPRI 61- 14)[5]。能力谱法也称为“替代结构法”，即用一个具有“等效刚度”和“等效阻尼比”的“等效弹性结构”代替原来的非线性结构，从而近似采用弹性反应谱理论计算结构的地震反应。能力谱法是通过增大结构阻尼比、降低弹性反应谱的值来考虑这种非线性地震反应的，准确确定高桩码头结构的等效阻尼比是准确计算地震下高桩码头最大位移的前提。

在现行标准中，MOTEMS和ASCE/COPRI 61- 14采用的等效阻尼比计算公式是Kowalsky[6]基于Takeda滞回模型提出的公式，而Takeda滞回模型是根据钢筋混凝土柱低周往复试验确定的[7]，将由构件滞回模型推得的等效阻尼比用于高桩码头体系上显然不尽合理。POLA和POLB采用的等效阻尼比的滞回阻尼部分是Grant等[8]利用时程分析得到的，针对的是建筑钢筋混凝土框架结构，建筑框架抗震设计通常是“强柱弱梁”，而高桩码头是“强梁弱柱”[3]，两种结构存在较大差异。另外，高桩码头是一种利用桩基将作用在上部结构的荷载传递到地基深处中的低矮建筑物，桩- 土作用不可忽视，土体的非线性变形加大了码头体系的柔性和阻尼，而前述标准采用的等效阻尼比计算公式均未考虑土体阻尼。目前有关桩- 土体系的等效阻尼比研究很少，仅Suarez等[9]针对桥梁结构利用时程分析确定了单桩体系在4种特定土体类型下(内摩擦角分别为30°和37°的砂土以及不排水抗剪强度为20和40 kPa的黏土)的体系等效阻尼比。由于高桩码头的岸坡通常是倾斜的，且土层类型较为复杂，另外高桩码头体系并不是单桩体系，因而将其用于高桩码头值得探究。

由于结构体系等效阻尼比对于结构目标位移的确定有较大影响，有必要对此进行深入分析和研究。本文将高桩码头体系的滞回耗能分为桩基塑性铰耗能和土体土弹簧耗能两部分，根据一个振动循环内“替代结构”的等效粘滞阻尼与高桩码头体系桩基塑性铰耗能和土弹簧耗能之和相等的原则，推导得到了高桩码头体系的等效阻尼比公式。通过两个高桩码头工程案例，采用本文等效阻尼比公式进行Pushover分析，并将采用本文等效阻尼比公式分析的码头目标位移与采用规范、标准及其他研究者的等效阻尼比公式计算的位移进行了比较。

1 码头体系等效粘滞阻尼

采用能力谱法进行结构Pushover分析时，结构的等效阻尼比ξeq为[10]：

式中：ξel为结构体系在弹性范围内的阻尼；ξhyst为滞回阻尼比，对应于结构体系非弹性变形时的能量耗散(滞回耗能)。

滞回阻尼比ξhyst可按下式确定[10]：

式中：ED为结构体系的滞回耗能；ES为结构体系的最大应变能。

对于按“能力保护”原则设计的高桩码头体系，桩和土体均对体系的阻尼有所贡献。图1所示为一双向等幅振动循环时码头结构面板处荷载- 变形滞回环，码头的变形Δm为桩的变形Δp和土体变形Δs之和。

图1 桩和土对体系滞回耗能的贡献Fig. 1 Contribution of piles and soil to the hysteresis energy of system

对于桩，其非线性变形主要发生于塑性铰，故桩对体系耗能的贡献为塑性铰的滞回耗能，如图2(a)所示，图中Mi,m和θi,m分别为第i个塑性铰的弯矩和转角。nP个塑性铰的总耗能为

式中：Ei,Dp为第i个塑性铰的滞回耗能；nP为码头桩形成塑性铰的总数目。

在高桩码头静/动力分析中，土体通常用非线性土弹簧表示[2- 5]，如图3(b)所示。土体对码头体系耗能的贡献为所有土弹簧的耗能之和，如图2(b)所示，图中fi,Sm和yi,m分别为第i个土弹簧的荷载和变形：

式中，Ei,Ds为第i个土弹簧的滞回耗能；nS为所有土弹簧的数目。

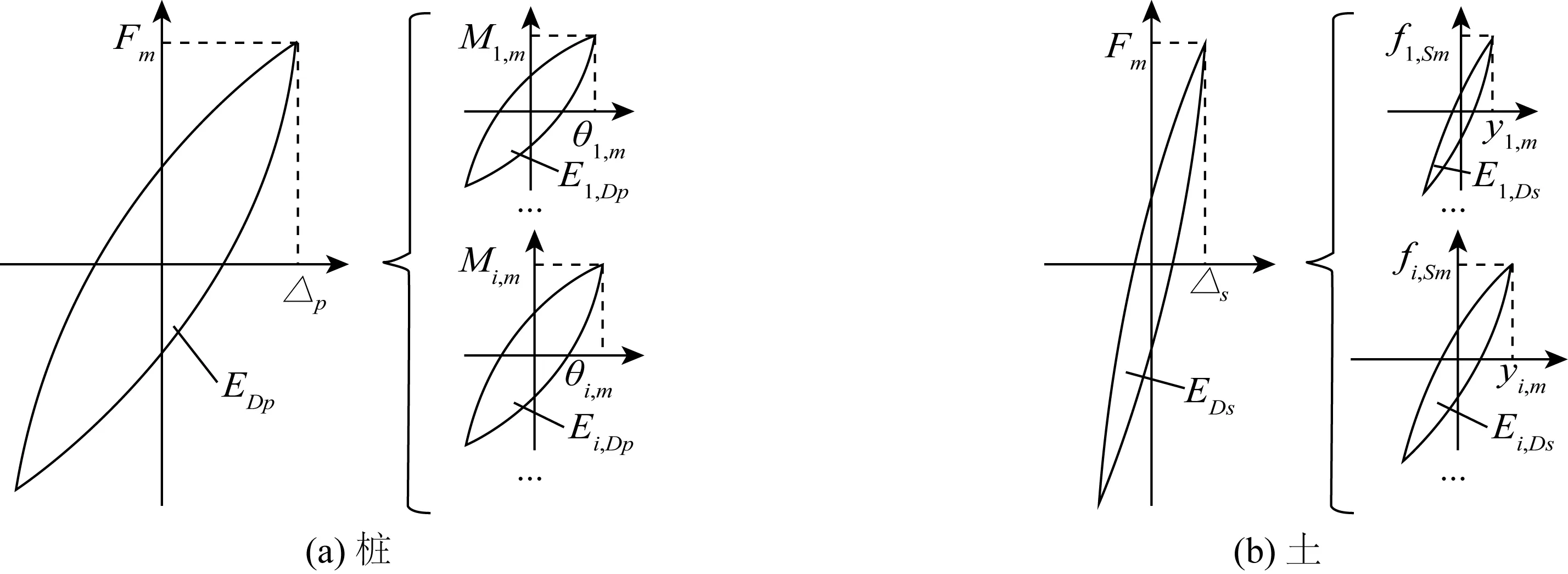
图2 桩和土的滞回耗能Fig. 2 Hysteresis energy of piles and soil

图3 高桩码头Pushover曲线和塑性铰形成顺序示例Fig. 3 Illustrative example of pushover curve and plastic hinges sequence for pile- supported wharf

对于倾斜岸坡上的高桩码头，在推覆过程中桩的塑性铰是依次形成的，如图3所示。当第j(0≤j≤nP)个塑性铰形成后(第j+1个塑性铰尚未形成)，码头体系的滞回耗能ED,j为j个塑性铰的滞回耗能与所有土弹簧的滞回耗能之和：

码头体系的应变能ES,j可按下式计算：

式中：Fj,m和Δj,m分别为第j个塑性铰形成后的水平力和面板位移。

由此，码头体系形成j个塑性铰时的滞回阻尼比ξhyst,j可按下式计算：

考虑弹性阻尼比ξel取0.05，高桩码头体系等效阻尼比的ξeq计算公式为：

式中：μnP,m为与ΔnP,m对应的位移延性系数，可按图4确定，μnP,m=ΔnP,m/Δy，图中K取Pushover曲线原点到曲线上桩首个塑性铰形成点连线的斜率，r为体系屈服后刚度与屈服前刚度之比。

2 桩和土弹簧的滞回耗能

按式(8)计算码头体系的等效阻尼比时，需要分别计算桩塑性铰和土弹簧的滞回耗能。下面分别给出两者的计算公式。

2.1塑性铰滞回耗能Ei,Dp

2.1.1 钢筋混凝土桩

桩塑性铰的特性可用弯矩-转角(M-θ)关系描述。图5为用Takeda滞回模型表示的第i个钢筋混凝土截面塑性铰的弯矩-转角关系。第i个塑性铰的等效阻尼比ξi,hyst,p可按下式计算[6]：

图4 码头体系位移延性系数的确定Fig. 4 Determination of displacement ductility factor for system

图5 Takeda 滞回准则Fig. 5 Takeda hysteresis rule

塑性铰弹性应变能Ei,Sp=Mi,mθi,m/2，根据式(2)，第i个塑性铰的滞回耗能为

如图6所示，M-θ曲线的理想化可按等能量法进行，初始刚度ki,p取曲线原点到钢筋首次屈服点的连线的斜率，并利用理想化的曲线计算塑性铰延性系数μi,p=θi,m/θi,y和第二刚度系数αi。

图6 弯矩-转角曲线的理想化Fig. 6 Idealization of moment- rotation curve

图7 双线性滞回规则 Fig. 7 Bilinear hysteresis rule

2.1.2 钢管桩

第i个钢管桩截面塑性铰的弯矩-转角(M-θ)滞回规则采用图7所示的双线性模型，等效阻尼比ξi,hyst,p按下式计算：

第i个钢管桩截面塑性铰的Ei,Dp按式(12)计算，M-θ曲线的理想化按图6进行。

2.2土弹簧滞回耗能Ei,Ds

2.2.1 土弹簧荷载-变形关系的计算

土弹簧荷载-变形(fS-y)关系按图8由P-y曲线(P为单位桩长土抗力)确定。

图8 土弹簧荷载-变形关系的确定Fig. 8 Determination of load- deformation relation for soil spring

图9 软黏土的p- y曲线Fig. 9 p- y curve for soft clay

2.2.2 软黏土

循环荷载下软黏土中桩的p-y曲线如图9所示[11]。图中p为桩侧单位面积水平土抗力(kPa)；y为桩的实际水平变形(m)；yC=2.5εCD(m)；εC为未扰动土样室内不排水压缩试验中最大主应力一半时的应变值；D为桩径(m)；XR为极限水平土抗力转折点的深度，按文献[11]确定。对于不排水抗剪强度为c≤96 kPa的软黏土，桩侧单位面积极限土抗力pu(kPa)按文献[11]确定。对于软黏土，第i个土弹簧恢复力fi,S=piDli，由此可以利用软黏土p-y曲线确定土弹簧荷载-位移关系的骨架曲线fi,S=g(yi)。由图9得：

采用Masing准则[12]确定土弹簧的加卸载荷载-位移关系曲线，如图10所示。根据图10和式(13)可得:

第i个土弹簧的滞回耗能Ei,Ds按滞回环包围的面积计算，即

令g1(yi)=0，g2(yi)=0，得yi,1=0.75yi,m，yi,2=-0.75yi,m，从而

以上推导针对yi≤3yi,C的情况，考虑到一般情况下土弹簧的变形不会超过3yi,C，对于yi>3yi,C的情况，为简化计算，直接取yi,m=3yi,C时的滞回耗能，故第i个土弹簧的滞回耗能为：

图10 软黏土中土弹簧骨架曲线和滞回环Fig. 10 Backbone curve and hysteretic loop of soil spring in soft soil

图11 砂土中土弹簧骨架曲线和滞回环Fig. 11 Backbone curve and hysteretic loop of soil spring in sand

2.2.3 砂土

循环荷载下砂土中桩的P-y曲线为[11]

式中：P为单位桩长的水平土抗力(kN/m)；A为系数，取0.9；Pu为单位桩长砂土的极限水平土抗力(kN/m)，按文献[11]确定；k为土抗力的初始模量(kN/m3)，根据内摩擦角φ按文献[11]确定；y为桩的水平变形(m)；H为深度(m)。对于砂土，第i个土弹簧恢复力fi,S=Pili，由此可利用砂土的P-y曲线确定土弹簧荷载-位移关系的骨架曲线fi,S=g(yi)。根据式(19)，可得

与软黏土相似，仍采用Masing准则确定土弹簧的加卸载荷载-位移关系曲线，如图11所示。采用前述的推导方法，得第i个土弹簧的滞回耗能Ei,Ds：

2.2.4 抛石

对于岸坡抛石，第i个土弹簧恢复力fi,S=Pili，其中单位桩长的土抗力Pi可根据文献[13]按图12确定，图中“GL”指地面，由此确定土弹簧荷载-位移关系的骨架曲线。

如图13所示，近似采用双线性滞回规则确定抛石中土弹簧的滞回环，其中近似认为在屈服点C(yi,t，fi,Sm)和C′(-yi,t，-fi,Sm)之间的加卸载路径相同，无能量耗散。第i个土弹簧的滞回耗能Ei,Ds可以用滞回环包围的面积计算，根据几何关系得：

图12 码头设计中常用的抛石P- y曲线Fig. 12 P- y curves of rockfill typically used for wharf design of soil spring in rockfill

图13 抛石中土弹簧骨架曲线和滞回环Fig. 13 Backbone curve and hysteretic loop

3 案例分析

3.1案例I

3.1.1 工程概况

某海外强震区高桩码头断面如图14所示，码头宽28.87 m，排架间距6.3 m，面板厚0.45 m。圆形实心混凝土桩直径0.8 m，横梁高1.9 m，宽1.5 m；前边梁高2.2 m，宽1.5 m；轨道梁高1.9 m，宽1.6m；中纵梁高1.9 m，宽1.5 m；后边梁高1.9 m，宽1.5 m，码头面堆载为40 kPa。当地平均海平面为1.2 m。C、D和F桩与上部结构的连接如图15所示，其它各桩类似。土层物理力学参数列于表1，基岩面高程为-34.5 m。

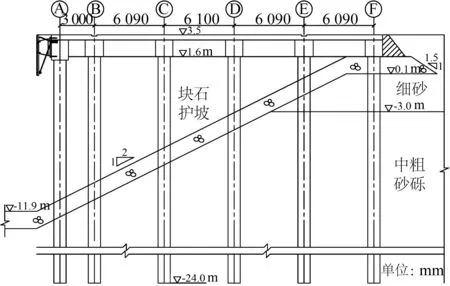
图14 码头断面Fig. 14 Section of wharf

图15 桩与上部结构连接Fig. 15 Pile- wharf connection

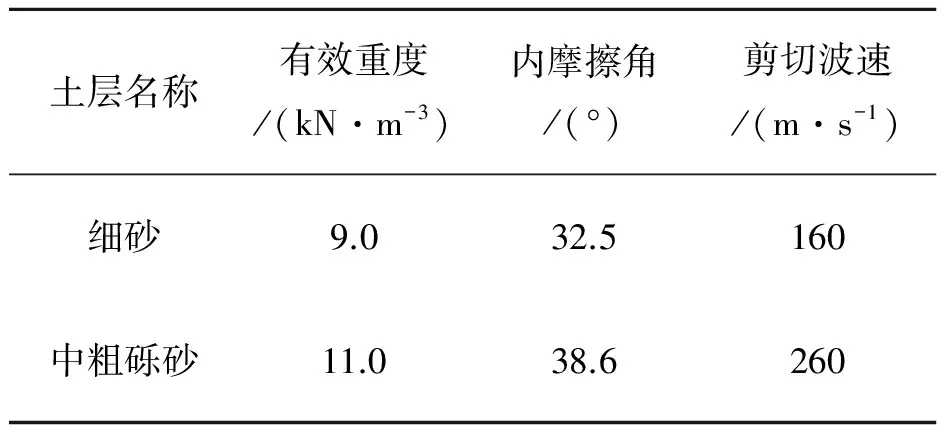
表1 土层物理力学参数Tab. 1 Physical and mechanical parameters of soil layers

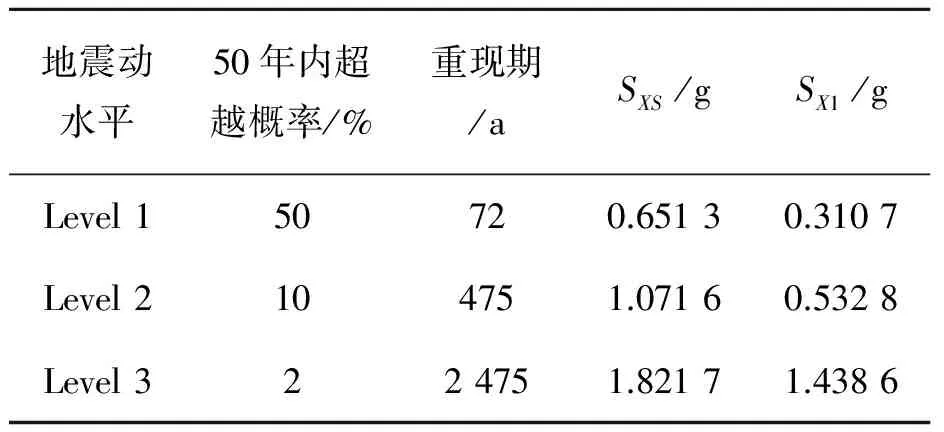
表2 设计地震动参数Tab. 2 Design ground motion parameters

3.1.2 设计地震动

参考美国POLB标准，确定3个设计地震水准，如表2所示，表中SXS和SX1分别为考虑场地类别的短周期和周期为1 s的谱加速度值。设计加速度反应谱按MOTEMS确定，如图16所示，图中BS和B1分别为修正短周期和1 s周期谱反应的粘滞阻尼系数，可根据阻尼比按MOTEMS确定；T为结构基本周期。

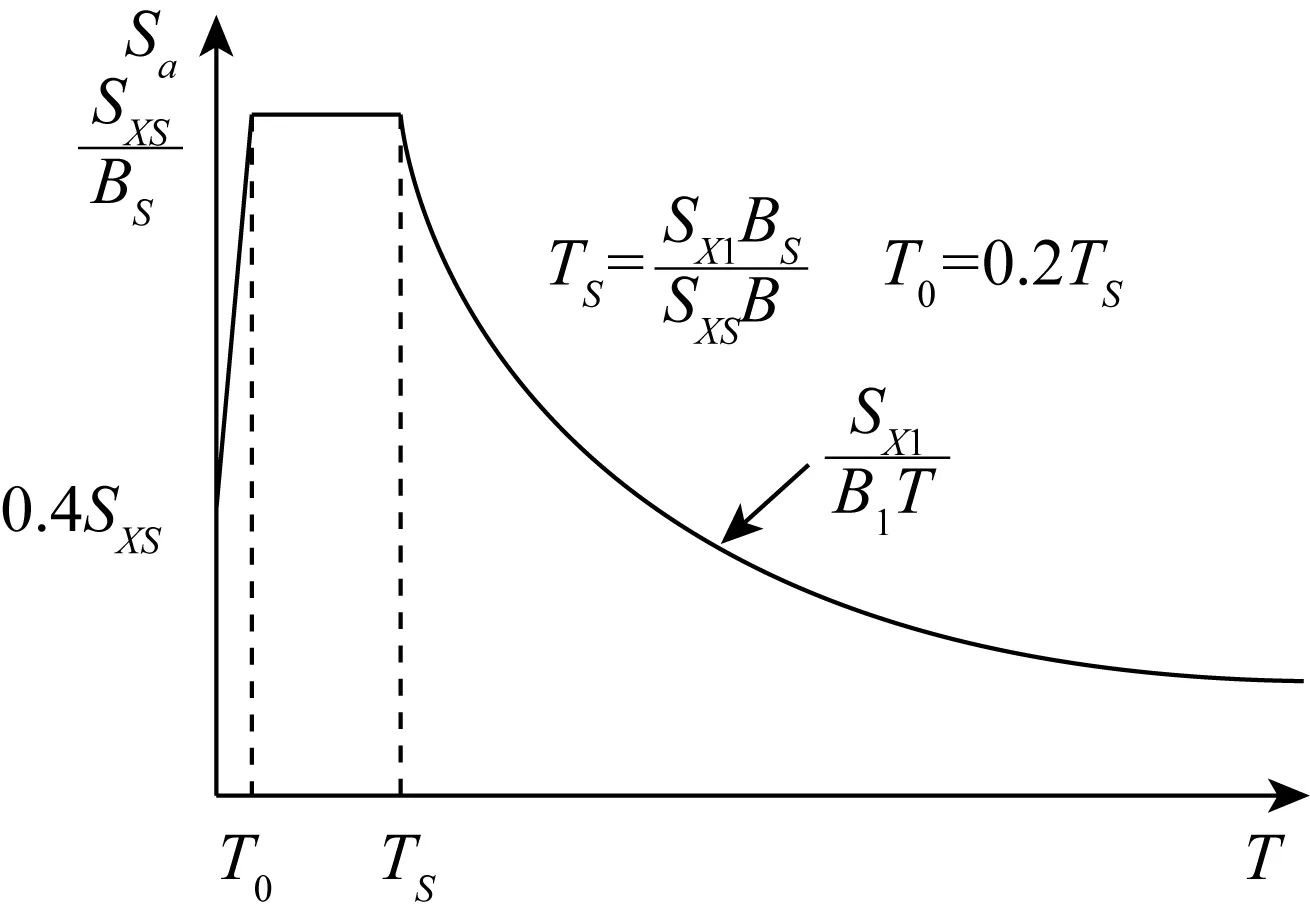
图16 设计加速度反应谱Fig. 16 Design acceleration response spectrum

图17 Pushover曲线和塑性铰形成顺序Fig.17 Pushover curve and plastic hinges sequence

3.1.3 Pushover曲线

3.1.4 码头体系等效阻尼比

利用软件的后处理功能，得到塑性铰弯矩-转角曲线和弹簧荷载-变形曲线。由于等效阻尼比通常表示为与位移延性系数的关系，可按图4计算不同面板位移对应的延性系数，如图18所示。选取一系列面板位移，得到与该位移对应的塑性铰弯矩和转角以及弹簧荷载和变形，然后根据式(10)计算塑性铰耗能，按式(21)和式(22)计算土弹簧耗能，如图19所示。根据土弹簧和塑性铰耗能按式(8)计算高桩码头体系的等效阻尼比，如图20所示。为分析桩-土相互作用对体系阻尼的影响，通过去除式(8)中土弹簧耗能部分得到了未考虑桩-土相互作用的等效阻尼比。另外，图20还给出了按ASCE/COPRI 61- 14、POLB和Suarez[9]计算的等效阻尼比，以与本文提出的等效阻尼比计算结果对比。其中，图20(a)为滞回阻尼比，图20(b)为体系等效阻尼比。

图18 面板位移与位移延性系数的关系Fig. 18 Relationship between deck displacements and displacement ductility factors

图19 塑性铰和土弹簧耗能Fig.19 Dissipated energy of plastic hinges and soil springs

图20 高桩码头体系等效阻尼比Fig. 20 Equivalent damping ratio of pile- supported wharf

由图19可以看出，土体耗能占体系总耗能的比例较大，而且在滞回阻尼比上也得到了体现，如图20(a)所示。由图20(a)可以看出，由于未考虑桩-土相互作用，抗震设计标准中等效阻尼比公式中的滞回阻尼比部分均小于本文提出的公式，而且在延性系数小于1时均为零；Suarez模型虽然考虑桩-土相互作用，但是其针对是单桩和水平土层，而且土的类型与本案例亦不十分契合，故其计算结果与本文相比亦有较大差异；另外，由于不同阻尼比计算公式采用的弹性阻尼比存在差异(ASCE/COPRI 61- 14取5%，POLB取10%，Suarez取2%～3%并根据文献[14]对弹性阻尼比进行修正)，故图20(b)中POLB的等效阻尼比计算结果在延性系数μ<6时与本文较为接近，但随着延性系数的增大，二者的差距逐渐变大。

3.1.5 目标位移

根据表2中的地震动参数，进行Pushover分析得到Level 1、Level 2和Level 3地震动下采用不同等效阻尼比计算公式的目标位移，如图21所示。

图21 设计地震动下的目标位移Fig. 21 Target displacements under design ground motion

从图21可以看出，在Level 1和Level 2地震动下，POLB和本文(考虑桩-土相互作用)提出的等效阻尼比模型的计算结果更为接近，在Level 3地震动下二者的差距变大，这正好与图20(b)中二者等效阻尼比的变化趋势相同；由于本文(考虑桩-土作用)计算模型的等效阻尼比计算结果较大，故相应地震下的耗能越大，位移反应越小，而其它模型则位移反应较大；将本文(未考虑桩-土相互作用)计算模型的计算结果与ASCE/COPRI 61- 14对比可以发现，将构件的阻尼比计算公式用在体系上会低估结构的位移反应，偏于不安全。

3.2案例II

3.2.1 工程概况

除土体参数外，码头的结构型式和材料参数与案例I相同。岸坡为均质黏土，黏土的有效重度为9.0 kN/m3，不排水抗剪强度标准值为48 kPa。

3.2.2 设计地震动

设计地震水准如表3所示，设计加速度反应谱按MOTEMS确定，如图16所示。

3.2.3 Pushover曲线

水平荷载作用下码头的荷载-变形曲线和塑性铰形成顺序如图22所示。

表3 设计地震动参数Tab.3 Design ground motion parameters

图22 Pushover曲线和塑性铰形成顺序Fig. 22 Pushover curve and plastic hinges sequence

3.2.4 码头体系等效阻尼比

计算不同面板位移对应的延性系数，如图23所示。采用案例I的方法，计算得到塑性铰和土弹簧耗能，如图24所示，并计算高桩码头体系的等效阻尼比，如图25所示。

由图24可以看出，相比于案例I，土体耗能占体系总耗能的比例更大，因为土质较软，土体变形更大，对体系变形的贡献更大。由图25可以看出，不同等效阻尼比计算模型的差异与案例I相似，不再赘述。

图23 面板位移与位移延性系数的关系 Fig. 23 Relationship between deck displacements and displacement ductility factors

图24 塑性铰和土弹簧耗能Fig. 24 Dissipated energy of plastic hinges and soil springs

图25 高桩码头体系等效阻尼比Fig. 25 Equivalent damping ratio of pile- supported wharf

3.2.5 目标位移

根据表3中的地震动参数，进行Pushover分析得到Level 1、Level 2和Level 3地震动下采用不同等效阻尼比计算公式的目标位移，如图26所示。

图26 设计地震动下的目标位移Fig. 26 Target displacements under design ground motion

从图26可以看出，在Level 2和Level 3地震动下，POLB和本文(考虑桩-土相互作用)提出的等效阻尼比模型的计算结果较为接近，而在Level 1地震动下二者的差距铰大，这正好与图25(b)中二者等效阻尼比的变化趋势相同；与案例I相同，将构件的阻尼比计算公式用在体系上会低估结构的位移反应，偏于不安全。通过对比图21和图26可以看出，土体类型的不同对体系等效阻尼比有较大影响，规范采用的公式并不能反映这一不同，而本文提出的公式可以很好地反映这一现象。

4 结 语

将高桩码头体系的滞回耗能分为塑性铰耗能和土弹簧耗能两部分，基于一个振动循环内高桩码头体系与“替代结构体系”耗能相等的原则，提出了考虑桩-土相互作用的高桩码头体系等效阻尼比计算公式。经研究得出如下结论：

1) 土体耗能对高桩码头体系阻尼贡献较大，在静力非线性分析中不可忽略；

2) 将由构件得出的等效阻尼比计算公式用在高桩码头体系上会低估结构在地震作用下的位移反应，偏于不安全；

3) 岸坡土体类型对高桩码头体系的耗能有较大影响，本文提出的公式可以较好地反映这一现象；

4) 根据码头各桩塑性铰出现顺序和转动情况计算码头体系的等效阻尼比更符合实际情况，可以更好地反映高桩码头的结构特点。

[1] 高树飞, 贡金鑫. 基于位移的高桩码头抗震设计方法[J]. 水运工程, 2014,(10):39- 46. (GAO Shufei, GONG Jinxin. Displacement- based seismic design method for pile- supported wharf [J]. Port & Waterway Engineering, 2014, (10):39- 46(in Chinese))

[2] California Building Code, Chapter 31F. Marine oil terminal engineering and maintenance standards (MOTEMS) [S].

[3] Port of Long Beach, Wharf design criteria (Version 3.0) [S]. 2012, Long Beach, CA.

[4] The Port of Los Angeles, Code for seismic design, repair, and upgrade of container wharves[S]. 2010,Los Angeles, CA.

[5] ASCE/COPRI 61- 14, Seismic design of piers and wharves[S].

[6] KOWALSKY M J. Displacement- based design—a methodology for seismic design applied to RC bridge columns [D]. La Jolla: University of California at San Diego, 1994.

[7] DWAIRI H M, KKOWALSKY M J, NAU J M. Equivalent damping in support of direct displacement- based design [J]. Journal of Earthquake Engineering, 2007, 11(4):512- 530.

[8] GRANT D N, BLANDON C A, PRIESTLEY M J N. Modeling inelastic response in direct displacement- based design[R]. Report No. ROSE 2004/02, European School of Advanced Studies in Reduction of Seismic Risk, Pavia, Italy.

[9] SUARE V, KOWALSKY M J. Displacement- based seismic design of drilled shaft bents with soil- structure interaction [J]. Journal of Earthquake Engineering, 2007, 11(6):1010- 1030.

[10] BLANDON C A, PRIESTLEY M J N. Equivalent viscous damping equations for direct displacement based design [J]. Journal of Earthquake Engineering, 2007, 9(2):257- 278.

[11] API RP 2A- WSD- 2005, Recommended practice for planning, designing and constructing fixed offshore platforms—working stress design[S].

[12] 陈国兴.岩土地震工程学[M].北京:科学出版社,2007. (CHEN Guoxing.Geotechical earthquake engineering[M].Beijing:Science Press,2007. (in Chinese))

[13] KAWAMATA Y. Seismic performance of a pile- supported container wharf structures in rockfill [D]. Oregon: Oregon State University, 2009.

[14] PRIESTELY M J N, CALVI G M, KOWALSKY M J. Displacement- based seismic design of structures [M]. IUSS Press, Pavia, ITALY, 2007.

[15] 程泽坤. 基于P- Y曲线法考虑桩土相互作用的高桩结构物分析[J]. 海洋工程, 1998, 16(2):73- 82. (CHENG Ze- kun. Analysis of high- pile structures based on P- Y curve method with consideration of interaction between pile and soil [J]. The Ocean Engineering, 1998, 16(2):73- 82. (in Chinese))

[16] 李颖，贡金鑫，吴澎. 高桩码头抗震性能的pushover分析[J]. 水利水运工程学报, 2010,(4):73- 80. (LI Ying, GONG Jinxin, WU Peng. Research on pushover analysis method for seismic performance of pile- supported wharf structure [J]. Journal of Hydro- Science and Engineering, 2010, (4): 73- 80. (in Chinese))

[17] 李颖，贡金鑫. 考虑桩土相互作用的高桩码头非线性地震反应分析[J].水利水运工程学报,2010,(2):92- 99. (LI Ying, GONG Jinxin. Nonlinear seismic response considering soil- pile analysis of wharf structure dynamic interaction [J]. Journal of Hydro- Science and Engineering, 2010, (2):92- 99. (in Chinese))

Equivalent damping ratio and pushover analysis for pile- supported wharf system
considering pile- soil interaction

GAO Shufei1，GONG Jinxin1, FENG Yunfen2

(1. The State Key Laboratory of Coastal and Offshore Engineering, Dalian University of Technology, Dalian 116024, China; 2. School of Architecture and Civil Engineering, Liaocheng University, Liaocheng 252059, China)

In order to determine the equivalent damping ratio for pile- supported wharf system considering pile- soil interaction, this paper features the incorporation of energy dissipated by soil and integration of energy dissipation of a single plastic hinge of piles in the pushover analysis of pile- supported wharf using capability spectrum method. The energy dissipated by soil is quantified based on the p- y curve of the soil springs and the Masing hysteretic rule, and the total energy dissipated by the structure is the sum of the energy dissipated by all the plastic hinges that appear in the piles corresponding to certain lateral displacement. The equivalent viscous damping ratio of pile- supported wharf system as a whole is derived through equating the energy dissipation of pile- supported wharf system with a corresponding viscous system in a complete cycle under sinusoidal excitation. In addition, two case studies are performed utilizing the proposed model. It indicates that it is more reasonable to account for the contribution of energy dissipation of pile- soil interaction and the energy dissipating mechanism of plastic hinge of piles for the response evaluation of pile- supported wharf by capacity spectrum method.

pile- supported wharf; seismic design; equivalent damping ratio; pile- soil interaction; hysteresis damping; pushover analysis

U656.1

A

10.16483/j.issn.1005- 9865.2015.05.004

1005- 9865(2015)05- 024- 11

2014- 11- 26

国家自然科学基金资助项目(51278081)；交通运输部项目“强震区港口工程结构抗震设计研究”资助项目(JTSBD 2013 02 130)

高树飞(1989- )，男，博士研究生，从事港口工程结构抗震设计方法研究。E- mail: gaosf1989@qq.com

贡金鑫。E- mail: gong_jx.vip@eyou. com