海底对系缆运动及张力影响研究

韦斯俊，戴愚志

(哈尔滨工业大学(威海) 船舶与海洋工程学院，山东 威海 264200)

海底对系缆运动及张力影响研究

韦斯俊，戴愚志

(哈尔滨工业大学(威海) 船舶与海洋工程学院，山东 威海 264200)

对系缆运动及张力进行分析，并考虑海底对系缆的影响。采用细长弹性杆单元模拟系缆微段，建立系缆运动控制方程，采用有限元法对其进行离散，将海底弹性和阻尼作用力添加到离散控制方程中。利用牛顿法和Newmark-β法对离散后的系缆非线性运动方程组进行数值求解。模拟长600 m的系缆顶端受到垂向正弦激励时的运动，分别求得考虑和不考虑海底作用时系缆运动响应和动态张力。通过对比系缆的运动、速度和动态张力结果，发现海底的弹性阻尼作用对系缆的运动及张力特性有极大影响。上述研究工作为计算海底对系缆的作用力提供了新方法。

动态张力；系缆运动；海底作用；弹性阻尼；运动响应；悬链线；系泊系统

对于深水悬链线系泊系统，在锚固点附近的系缆会与海底发生接触，二者的相互作用非常重要，在设计阶段必须考虑。因此模拟系缆与海底的相互作用是系泊系统数值计算非常重要的部分。

传统的悬链线法忽略了海底对系缆的影响[1]，认为系缆与海底接触的流线段是水平的且无相互作用。另外，传统悬链线法不适用于非线性材料及动态耦合问题[2- 3]。近年来，国内外学者对系缆与海底的相互作用进行了深入的研究。Gobat[4]在研究系缆与海底的相互作用时，将海底视为线弹性刚度和阻尼的弹簧层。唐友刚等[5]基于集中质量法，将海底当作弹性基础，研究了系缆与海底碰撞对系缆运动和张力的影响。但集中质量法不适合于求解系缆材料非线性问题。Ran[6]利用细长弹性杆单元模拟系缆微段，采用有限元法计算系缆的运动及张力，并考虑海底弹性作用；Arcandra[7]在此基础上，采用相同的方法研究了系泊系统的材料非线性问题。Chen[8]采用该方法研究浮式结构物系泊系统，并提出利用弹性基础来模拟海底的垂向作用。细长弹性杆有限元法方法能够很好地解决系泊系统中的非线性问题，但是目前国内还没有利用该方法对海底与系缆的相互作用进行深入的研究。

本文采用细长弹性杆单元模拟系缆微段，根据有限元法建立系缆运动方程。采用弹性地基来模拟海底的垂向作用，同时考虑海底土壤垂向及水平方向的阻尼作用，将海底作用力添加到系缆的有限元离散方程中，对系缆进行动态计算，分析了系缆在海底作用下的运动及张力特性。

1 系缆运动方程的推导

1.1细长弹性杆理论

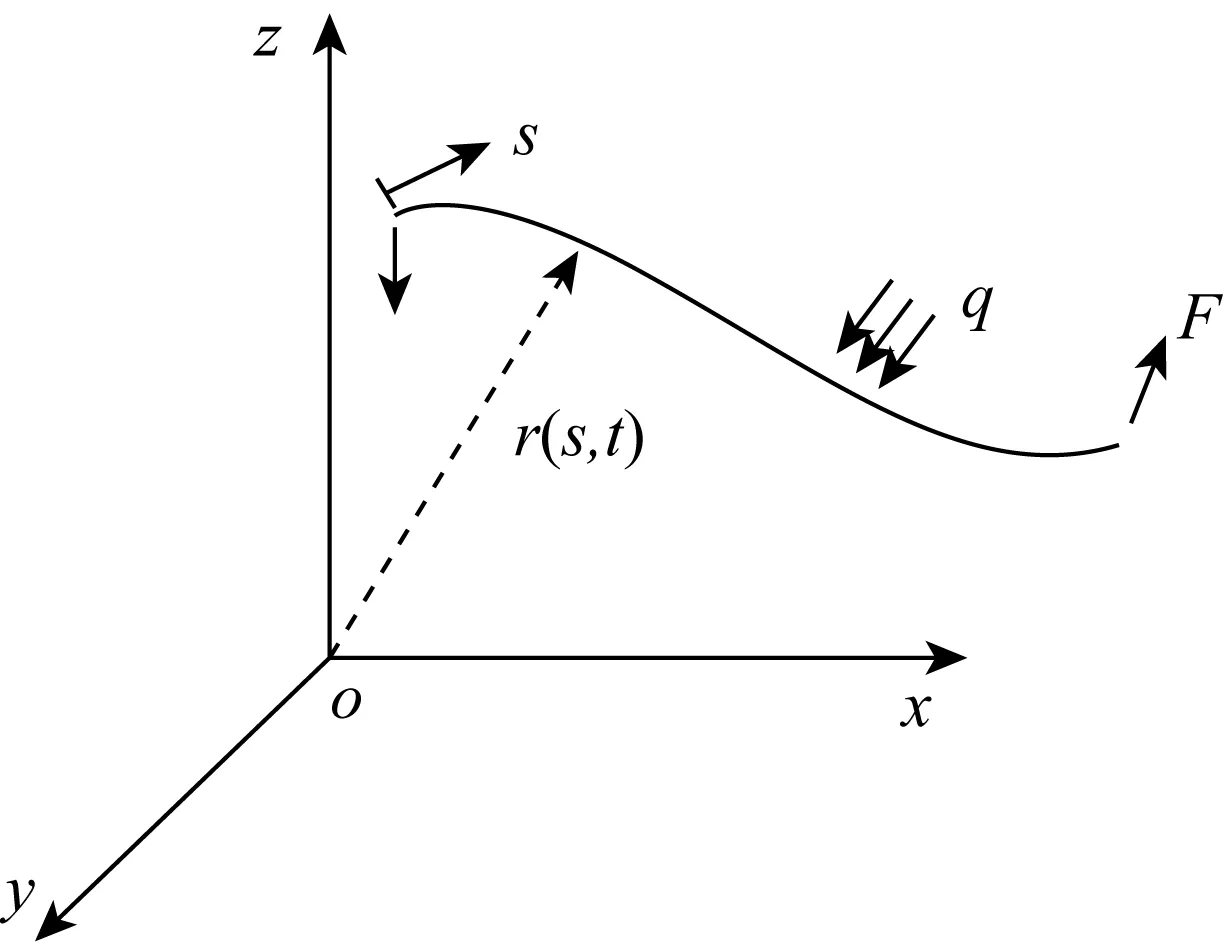
图1 细长弹性杆坐标系Fig. 1 The coordinate of slender rod

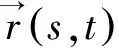
式中：EI表示弯曲刚度，H为扭矩。

将式(3)带入式(2)，可得

也可以写为：

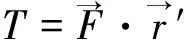
将方程(8)带入方程(1)，得到如下微分方程

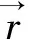
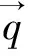
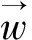
作用在杆件上的水动力载荷可由莫里森方程求得：

1.2有限元离散

将式(11)和式(13)写成张量的形式：

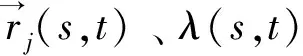
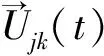
求解时不仅要求插值多项式Ak(s)和Pm(s)在插值基点处与函数数值相等，还要求在插值基点处导数相等，所以选用Hermite插值函数来求解。其中，Ak取三次Hermite形函数，Pm取二次Hermite形函数。

方程右端表示单元两端节点内力，在进行单元刚度阵总装时可消去。

同理，伸长条件为：

将式(25)中的每一项逐次积分，可得如下矩阵形式的运动微分方程：

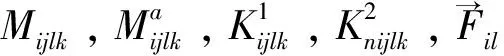
同理，对于可伸长条件式(26)有：

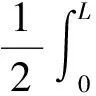
1.3静力问题

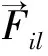
对非线性方程组式(29)、式(30)，可使用牛顿-辛普森法求解，当前迭代步n未知量的估计值假设为U(n)和λ(n)，应用泰勒级数在该值附近进行展开并忽略高阶项，写成矩阵的形式：

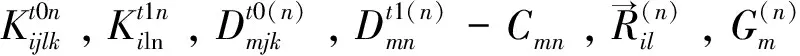
按照总体坐标系和参数Ujk和λn重新对方程中的量进行编号。重新编号以后，相应的系数阵中的元素排序也要改变，方程(31)可写为：

利用高斯法对此方程进行求解。要求解该方程，需要给出一个估计值作为迭代计算的初始值，从而求解得到Δy，然后通过y(n+1)=y(n)+Δy，得到新的y；重新计算切向刚度阵K和力向量F，再次求解Δy。迭代计算直到Δy小于设定好的误差限即可。

1.4动力问题

方程式(27)为单元的运动方程，将其与拉伸方程式(28)写为矩阵形式，如下：

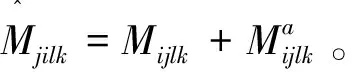
本文采用Newmark-β法对上述非线性微分方程进行求解。根据Newmark-β法，前后两个时间步的位移和加速度关系带入矩阵格式的细长弹性杆单元运动方程，并按照前述静力推导过程中的泰勒展开，最后可得到运动方程的增量形式：

2 海底作用

悬链线系泊系统在锚泊点处的系缆部分通常会与海底接触，发生相互作用。对于深水海洋平台悬链线系泊系统而言，随着水深的增加，海底作用力对系缆的影响变得更为重要。

将海底视为线弹性基础，系缆与海底接触，会发生碰撞，受到海底的弹性力fK；由于海底土壤松软，系缆会被海底土壤埋没，系缆在向上运动时，会受到海底土壤的抽吸作用，故在垂向上有阻尼力fD。系缆在垂直方向上的弹性力fK可以表示为[8]：

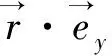
垂直方向的阻尼力fD可以表示为[10]：

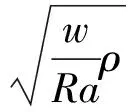
系缆在水平方向受到海底摩擦力，摩擦力fF的表达式如下[11]:

其中:系数Cf由下式求得：

式中：f为海底动态摩擦系数；vt为细长弹性杆单元切向速度；Cv为切向速度公差，Cv取值应足够小[12]。

将海底作用力添加到单元离散方程中，考虑到海底作用时，单元的运动方程可以写为：

式中：

海底对系缆的阻尼力和摩擦力只在动力计算时才需考虑，所以要对动力求解方程进行重构。

考虑到海底的动力作用，则有

3 算例分析

分析海底对系缆影响，对系缆进行动态计算。系缆长600 m，截面半径0.25 m，拉伸刚度为2.0×107N，弯曲刚度为3.125×105N·m2，单位长度湿重13.33 N/m，法向拖曳力系数为1.2，切向拖曳力系数为0.024，附加质量系数为2.0，初始预张力为3 600 N。本文研究的重点是系缆与海底的相互作用，故在计算时忽略流载荷的影响。假设系缆位于静水中，流速为0，初始时刻系缆处于静平衡状态，为了确保计算精度及保证系缆与海底接触部分存在单元节点，将系缆分为20段，节点编号从海底到海面为1到21。系缆的初始时刻位形如图2所示，节点1坐标为(0.0,0.0)，节点21的坐标为(430.0,365.0)。系缆顶点在垂向做受迫正弦运动z=5.0 sin(0.2πt)，幅值为5 m，周期为10 s。

采用Newmark-β法和牛顿法对海底的弹性阻尼作用进行二维X-Z数值计算。Newmark-β法的计算参数β取0.5,γ取0.75，动态计算模拟时间为120 s，时间步为0.1 s。

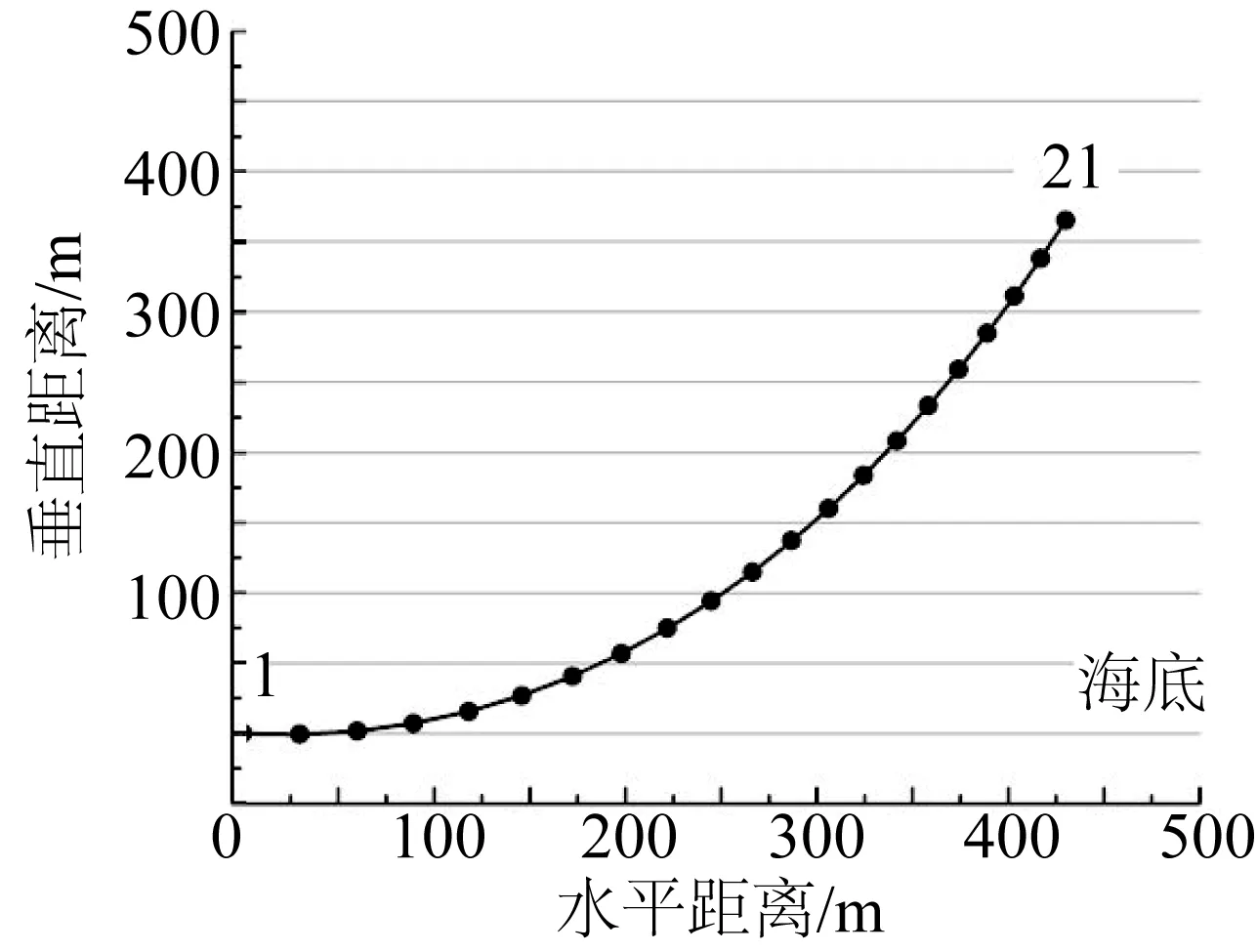
图2 系缆初始位形Fig. 2 Static line shape

图3 节点2垂向位移Fig. 3 Vertical displacement of node3

3.1海底作用对节点位移的影响

选取节点2和节点20作为观测对象，计算结果如图3至图5所示。图3为节点2的垂向位移随时间的变化，可以看到，考虑海底作用时，节点2与海底发生碰撞，其运动轨迹是无序的，不再呈现正弦规律，运动频率比不考虑海底作用时大，并且其坐标一直位于海底之上。

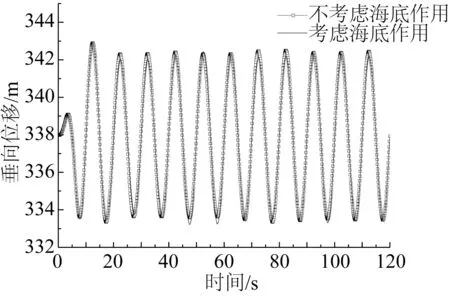
图4 节点20垂向位移Fig. 4 Vertical displacement of node 20

图5 节点2、3、4垂向位移Fig. 5 Vertical displacement of nodes 2,3,4

图4为节点20的垂向位移随时间的变化，由于节点20离海底较远，其受到海底作用的影响较小，其垂向运动和不考虑海底作用时基本一致。由图5可知，从海底到海面，随着与海底的距离变大，系缆的运动幅值逐渐变大，运动频率逐渐与顶部激励频率接近。

3.2海底对节点速度的影响

由于系缆顶点做垂向强迫运动，故系缆在垂直方向上的运动要比水平方向上的运动剧烈而明显。选取节点2和20垂直方向的速度为研究对象，如图6至图9。其中，图6和图7分别为不考虑海底作用和考虑海底作用时节点2的相图；图8和图9分别为不考虑海底作用和考虑海底作用时节点20的相图。

由图6和图7可以看到，不考虑海底作用时，节点2的运动很有规律，而考虑海底作用时系缆底部节点在运动过程中于海底有接触，受到海底的弹性碰撞、阻尼作用，运动变得随机混乱。节点20离海底较远，在顶部节点21周期运动的带动下，不管是否考虑海底作用，节点20的运动稳定且呈周期性。

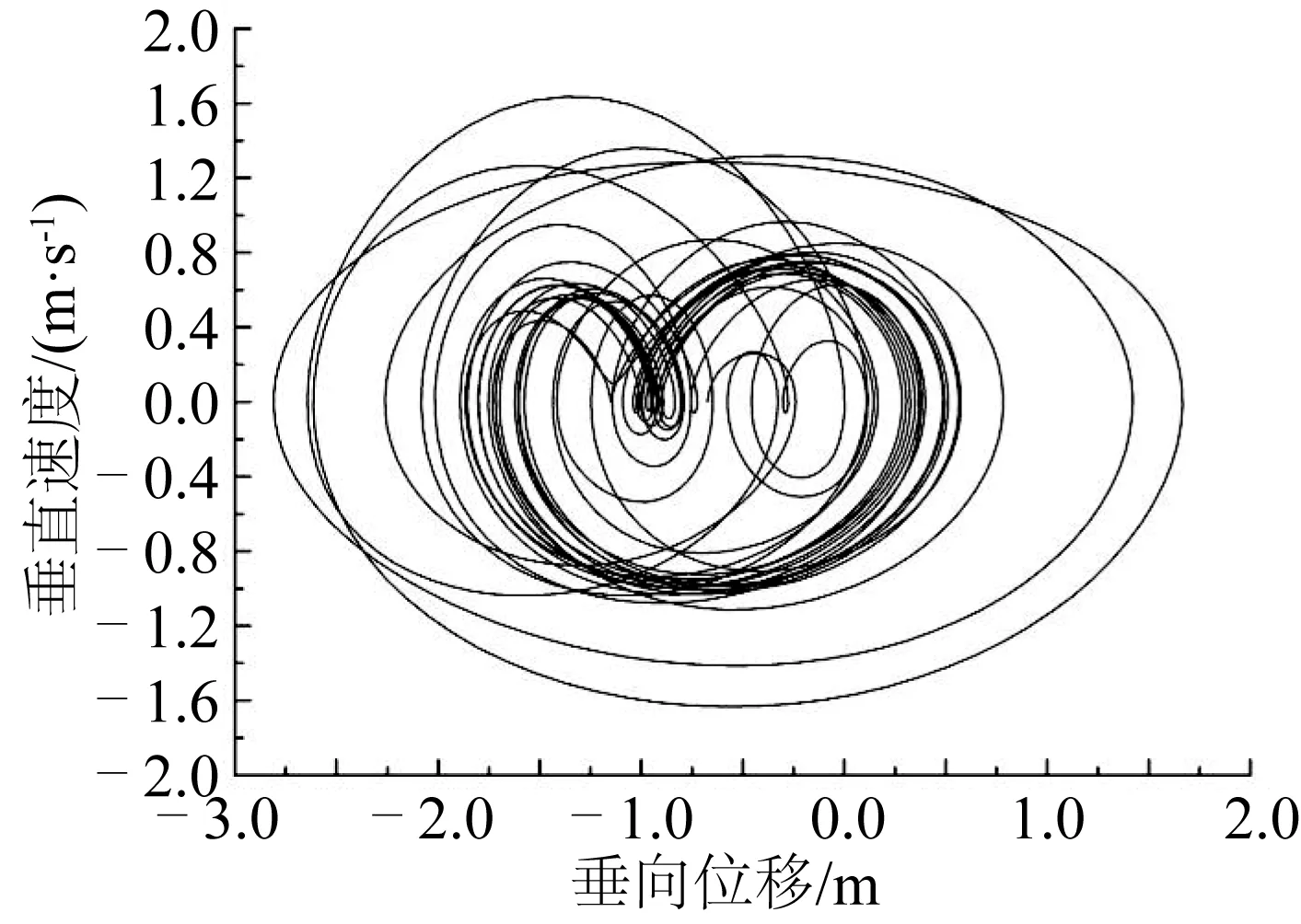
图6 不考虑海底作用节点2相图Fig. 6 Z velocity component of node 2 without seabed

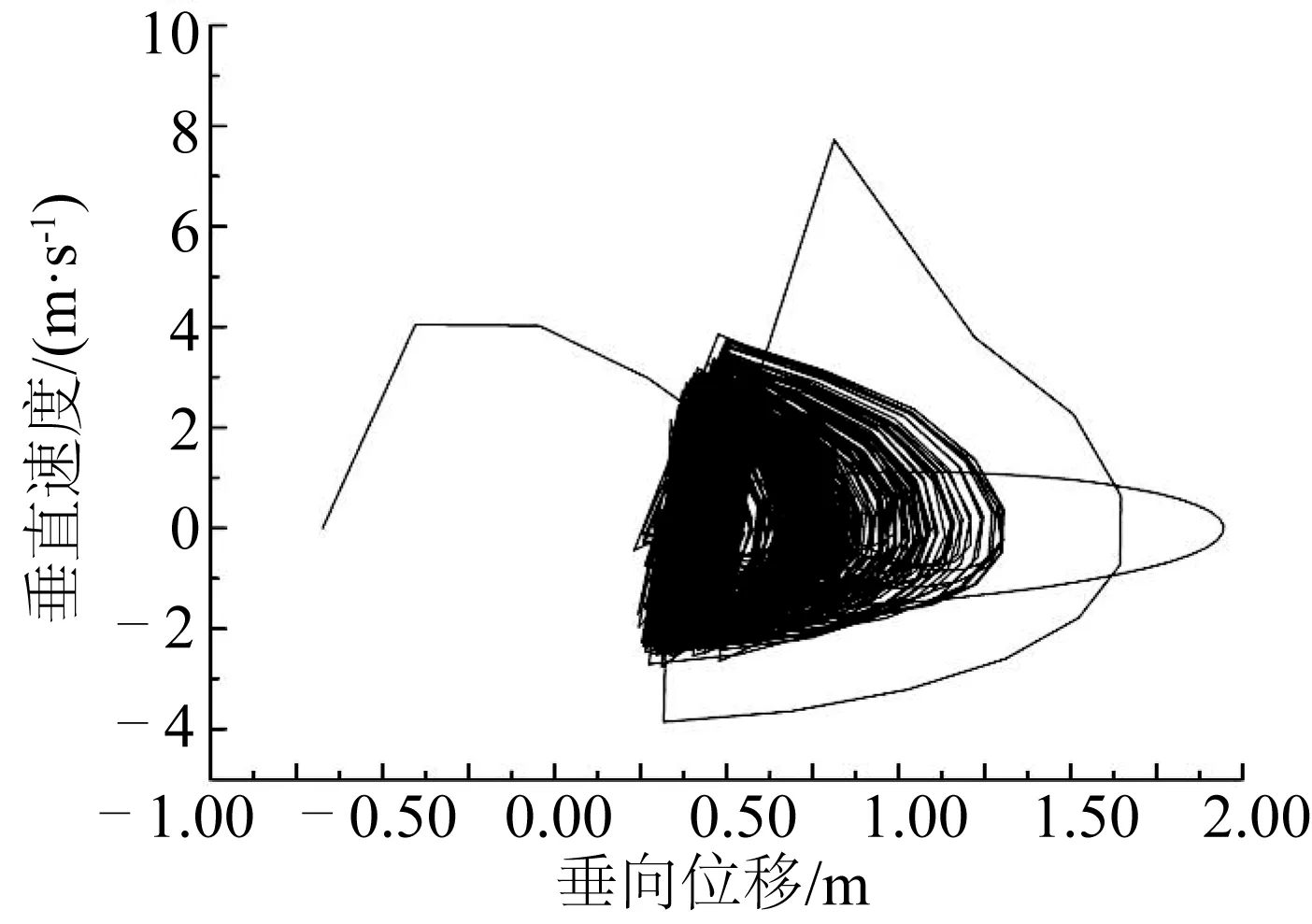
图7 考虑海底作用节点2相图Fig. 7 Z velocity component of node 2 with seabed

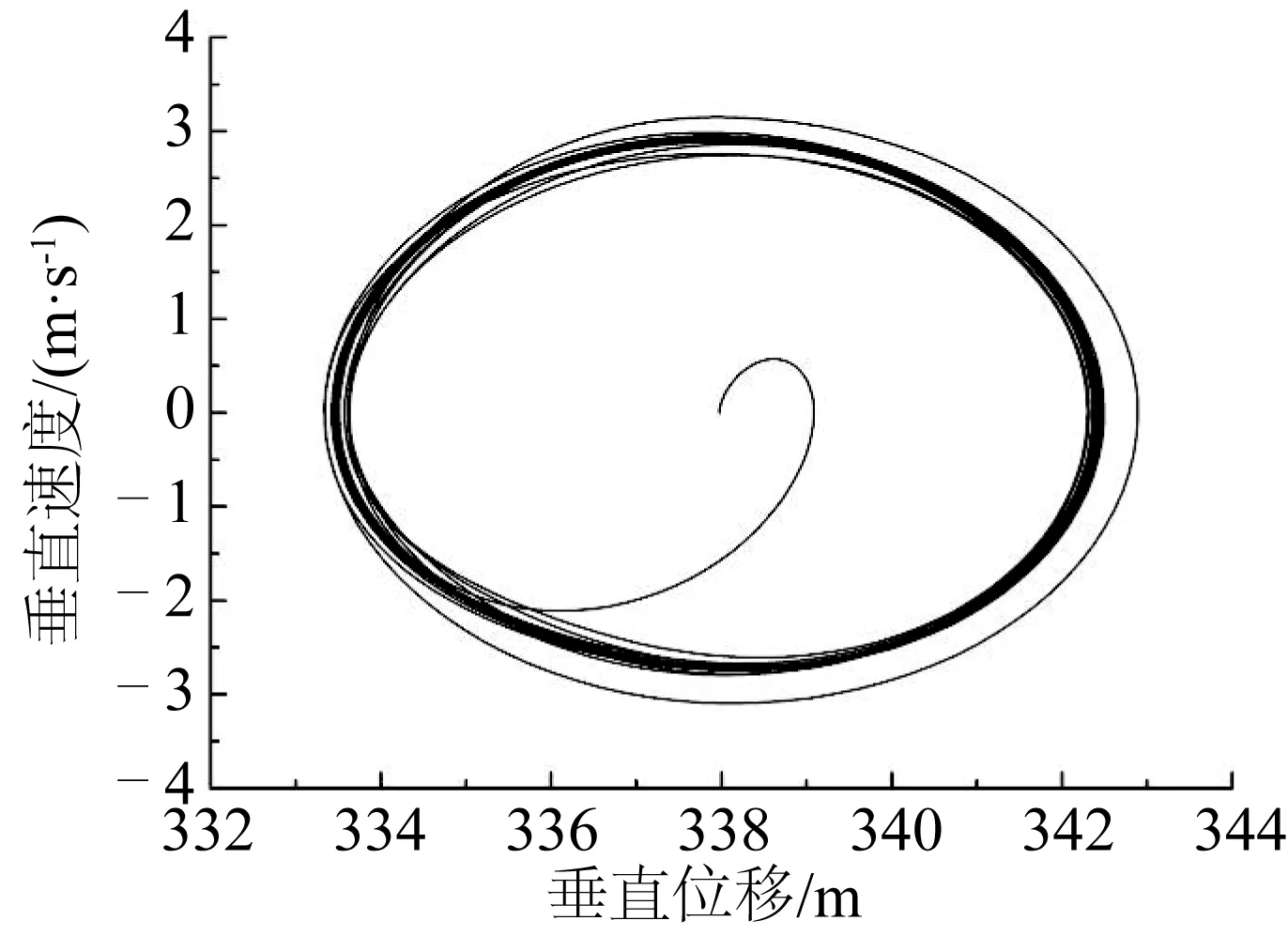
图8 不考虑海底作用节点20相图Fig. 8 Z velocity component of node 20 without seabed

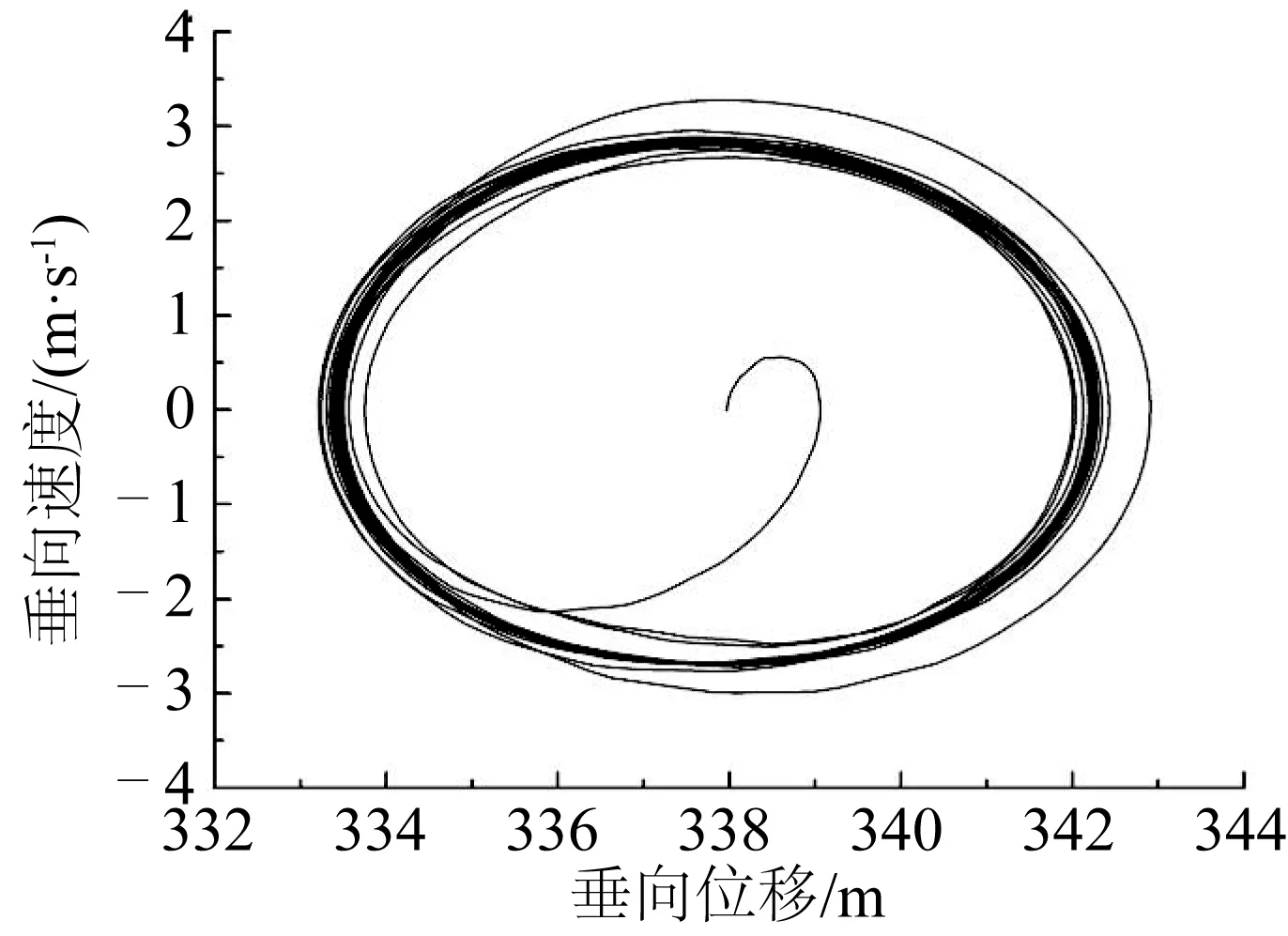
图9 考虑海底作用节点20相图Fig. 9 Z velocity component of node 20 with seabed

3.3海底对张力的影响

由于节点2与海底发生相互碰撞，故其动态张力与不考虑海底作用时差别很大，呈现非常不规则的震荡特性，见图10；而节点20由于距离海底较远，其动态张力受到的影响比节点2小，整体呈正弦趋势，在峰值处有小幅震荡，见图11。

由图12可知，系缆运动时会产生较大的动态张力；系缆底部与海底相互作用，使得系缆底部的动态张力显著增大，此时系缆中间部分的张力最小。

图10 节点2的动态张力Fig. 10 Dynamic tension at node 2

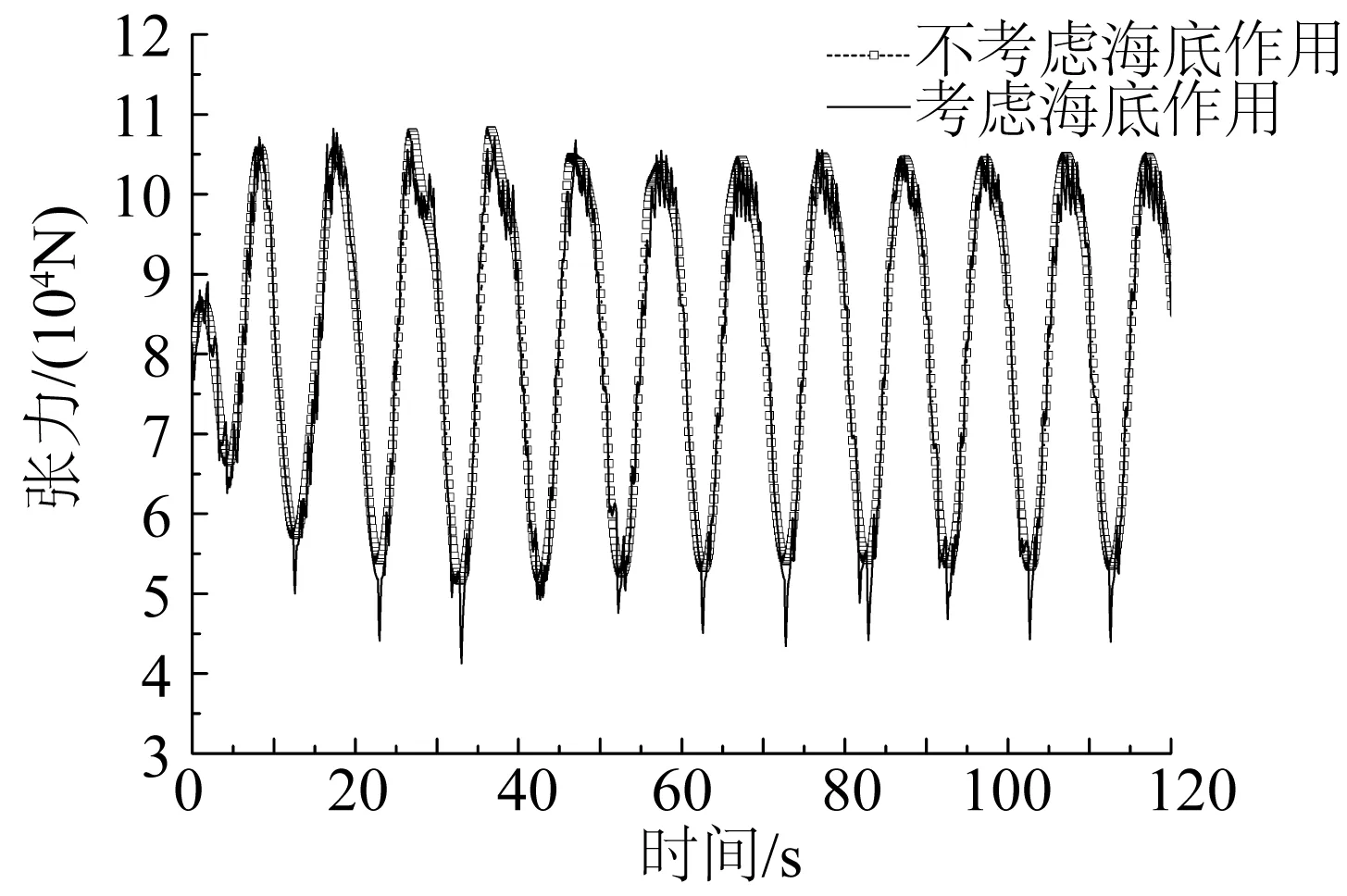
图11 节点20的动态张力Fig. 11 Dynamic tension at node 20

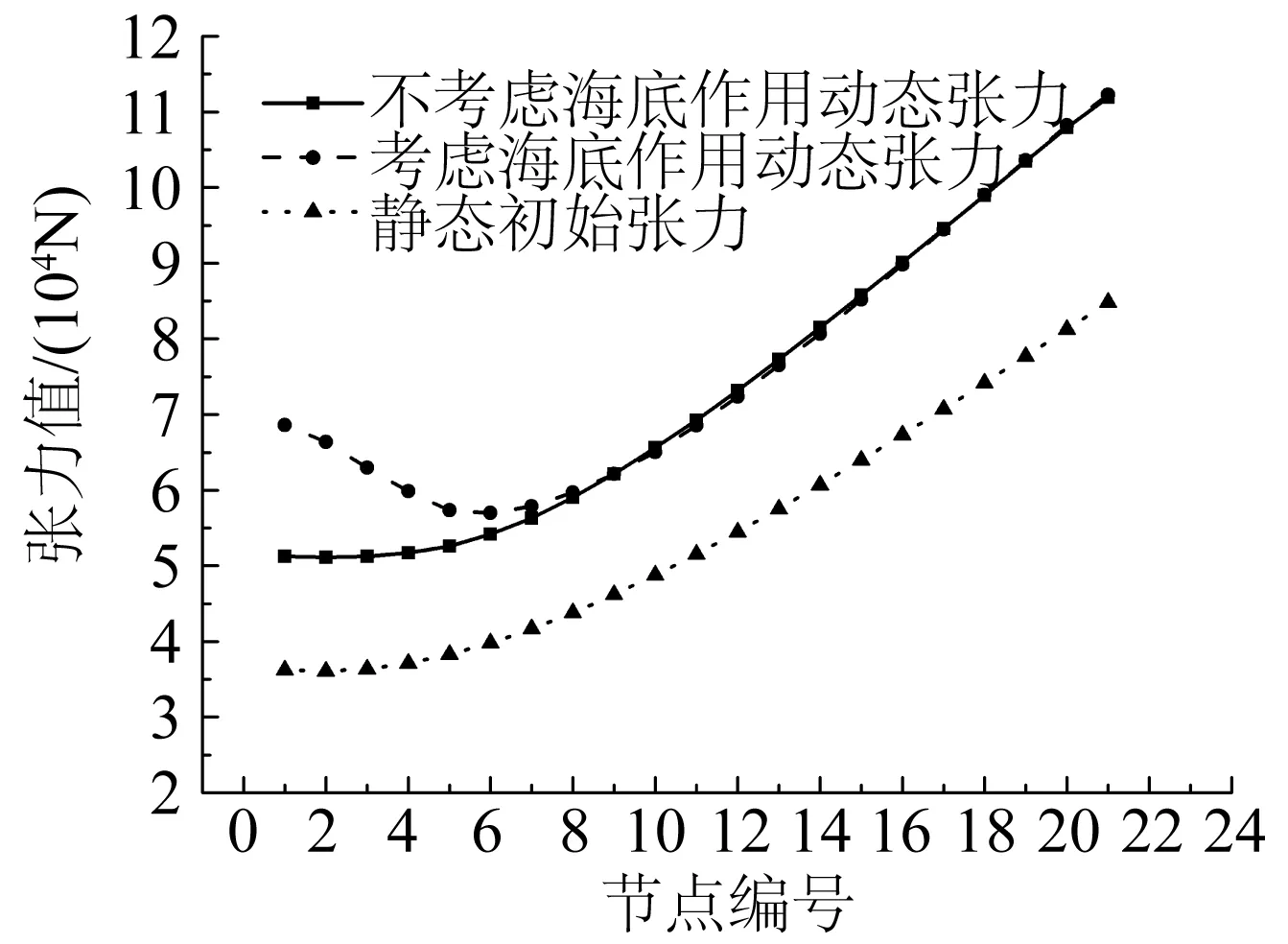
图12 系缆动态张力分布Fig. 12 Dynamic tension of mooring line

4 结 语

利用细长弹性杆单元模拟系缆微段，采用有限元法计算系缆的运动和张力。该方法能够直接在全局坐标系中处理系缆运动控制方程，不需要在不同的坐标系之间进行转换，而且能够很好地解决系缆研究中遇到的各种非线性问题。本文详细地给出了海底作用的有限元离散格式，并将其添加到系缆离散运动方程中，能够模拟海底土壤垂向弹性作用，以及海底土壤垂向和切向阻尼作用。由计算结果可知，海底对系缆的运动和张力有明显的影响。由于海底的作用，使得系缆触底部分的运动发生明显变化，运动频率变大，动态张力明显变大。所以，在研究深海结构物的系泊系统时，考虑海底对系缆的作用非常重要。

[1] 杨建民, 肖龙飞, 葛春花. 船舶与海洋工程环境载荷[M]. 上海：上海交通大学出版社，2008. (YANG Jianmin, XIAO Longfei, GE Chunhua. Sealoads on ships and offshore structures[M]. Shanghai：Shanghai Jiao Tong University Press, 2008. (in Chinese))

[2] 孟庆飞, 黄维平. 钢悬链线立管与海底相互作用弹性基础梁模拟方法研究[J]. 海洋工程, 2013, 31(4): 74- 78.( MENG Qingfei, HUANG Weiping. Simulation of SCR and seabed with elastic foundation beam model[J]. The Ocean Engineering, 2013, 31(4): 74- 78.(in Chinese))

[3] 乔东生, 欧进萍. 深水悬链锚泊线粘性阻尼计算[J]. 海洋工程, 2009, 28(4): 16- 22.(QIAO Dongshen, OU Jinping. Calculation on viscous damping of deepwater catenary mooring line[J]. The Ocean Engineering, 2009, 28(4): 16- 22. (in Chinese))

[4] GOBAT J I, GROSENBAUGH M A. Time- domain numerical simulation of ocean cable structures[J]. Ocean Engineering, 2006,33(10):1373- 1400.

[5] 唐友刚, 张若瑜, 易丛, 等. 考虑海底撞击力的系缆运动及张力分析[J]. 天津大学学报, 2008,40(11):1265- 1270. (TANG Yougang，ZHANG Ruoyu，YI Cong，et al. Analysis of motion and tension for cable considering the impact of seabed[J]. Journal of Tianjin University , 2008, 40(11):1265- 1270. (in Chinese))

[6] RAN Z. Coupled dynamic analysis of floating structures in waves and currents[D].Texas A&M University,2000.

[7] ARCANDRA. Hull/mooring/riser coupled dynamic analysis of a deepwater floating platform with polyester lines[D].Texas A & M University,2001.

[8] CHEN X. Studies on dynamic interaction between deep- water floating structures and their mooring/tendon systems[D].Texas A & M University,2002.

[9] 杨敏冬. 深水浮式结构与系泊/立管系统的全时域非线性耦合动态分析[D].大连：大连理工大学,2012. (YANG Mingdong. Full time- domain nonlinear coupled dynamic analysis of deepwater floating structures and Mooring/Riser Systems[D]. Dalian: Dalian University of Technology,2012. (in Chinese))

[10] NYGARD M K，SELE A，LUND K M. Design of a 25.5- in titanium catenary riser for the asgard B platform [C]//Proceedings of Offshore Technology Conference. Houston: OTC，2000: 343- 354.

[11] LINDAHL L，SJöBERG A. Dynamic analysis of mooring cables [C]//The Second International Symposium on Ocean Engineering and Ship and Handling. Gothenburg，1983: 281- 319.

[12] LIU Y, BERGDAHL L. Influence of current and seabed friction on mooring cable response: comparison between time- domain and frequency- domain analysis[J]. Engineering Structures, 1997,19(11): 945- 953.

Study on the effect of seabed on the motion and tension of the mooring line

WEI Sijun, DAI Yuzhi

(School of Naval Architecture and Ocean Engineering, Harbin Institute of Technology at Weihai, Weihai 264200, China)

In this paper, the motion and tension of mooring line are analyzed and the effect of seabed is considered. Slender elastic rod elements are used to model the segments of the mooring line. Governing equations of the motion of the mooring line are derived, discretized by finite element method. The stiffness and damping of seabed are included in the governing equations. Newton method and Newmark-βmethod are adopted to solve the discrete nonlinear equations of the mooring line. The motion of the mooring line of 600 meters length is simulated under the vertical sinusoidal excitation. The motion responses and dynamic tensions of mooring lines are obtained with or without the effect of seabed. By the comparison and analysis of the motion and velocity and dynamic tension, it can be found that the elastic damping of the seabed has much influence on the motion and tension of the mooring line. The present work provides a novel way for studying the effect of seabed on the mooring line.

dynamic tension; motion of mooring line; seabed impact; elastic damping; motion response; catenary; mooring system

P751

A

10.16483/j.issn.1005- 9865.2015.05.011

1005- 9865(2015)05- 081- 08

2014- 06- 05

韦斯俊(1988- )，男，广西人，硕士研究生，从事海洋结构物耐波性研究及系泊系统分析。E- mail:weisijunlz@gmail.com