弧形防波堤波浪力试验研究
2015-10-27赵利平朱亚州谢奥运邹俊飞
赵利平, 朱亚州 , 谢奥运, 邹俊飞
(1. 长沙理工大学 水利工程学院,湖南 长沙 410007; 2. 湖南省水沙科学与水灾害防治重点实验室,湖南 长沙 410004)
弧形防波堤波浪力试验研究
赵利平1,2, 朱亚州1,2, 谢奥运1,2, 邹俊飞1,2
(1. 长沙理工大学 水利工程学院,湖南 长沙 410007; 2. 湖南省水沙科学与水灾害防治重点实验室,湖南 长沙 410004)
在圆筒形防波堤和V形防波堤的基础上,结合离岸堤后形成V形和半圆形连续出现的韵律海岸的地貌平面形态特点,提出一种前墙为连续的半圆筒形防波堤形式。通过在波浪水槽内进行规则波物理模型试验,探究这一新型防波堤的波压力分布规律及波高、周期、水深等因素对波压力的影响。将试验结果与海港水文公式和合田良实公式计算的理论值对比分析,给出了以合田良实公式的折减系数来拟合新型弧形防波堤波浪总水平力的计算公式。结果表明:新型弧形防波堤上的波压力随波高、周期的增大而增大,其水平波浪总力比同等尺度直墙少10%左右。
圆筒防波堤;V形防波堤;半圆筒;波压力分布;波浪总水平力
随着水运事业的不断发展,船舶大型化的趋势越来越明显,港口建设必将向外海深水区发展。相应地,对作为主要港口水工建筑物的防波堤也提出了更高的要求。圆筒形结构由于能够适应外海水深浪大、地质条件复杂等要求得到了广泛的应用。圆筒结构所受的波压力为径向力,沿圆沉箱纵轴线波压力的水平分力将相互抵消,结构受力状态好。另外,圆筒结构还具有材料用量少、结构简单、预制安装方便等诸多优点。但是圆筒形防波堤也有其不足,由于迎浪面由多个半圆柱形曲面构成,波峰在接触到筒体后很快分向两侧推进。在两圆筒的接合处形成波峰汇集区,该区的波浪振幅要比筒前大很多,对底部护肩有严重的冲刷。对圆筒结构的强度计算也有很大影响[1]。因此,此种结构仍然有待改进。
1 模型设计
根据防波堤发展的历史和各国使用防波堤的经验,实体直立式防波堤的优化和改进一般通过以下四种方式以达到不同功能要求:改进堤的上部结构;改变墙面的几何形状;采用消波结构;在直立堤前建斜坡堤。总结前人研究成果,在各种结构优化思路的指引下,近年出现的V形浮式防波堤可以为防波堤的结构优化提供借鉴。该种防波堤俯视为V形,通过V形结构的尖端朝向波浪的来向,将来波展开和反射,使入射波在V形防波堤的内域中衰减,从而在防波堤内及防波堤的下风处“创造”一片静水。美国军方RIBS(Rapidly Installed Breakwater System)就是此种结构的典型范例,见图1。日本曾用类似装置作为油轮失事后防油污染的围栏[2- 3]。另外,在海岸防护中,为了防止海岸侵蚀,人们通过修建离岸堤来实现保滩促淤,离岸堤修建后,会在离岸堤和海岸之间形成V形和半圆形连续出现的类似韵律海岸的稳定岸线形态,能很好地适应波浪对海岸的冲击。由此种韵律海岸的地貌平面形态,从“遵循顺水之性,因势利导”的角度,可以在此基础上发展成一种稳定的护岸结构,这也符合对传统防波堤进行的改进。见图2。

图1 V式防波堤Fig. 1 V- shaped breakwater

图2 离岸堤后形成V形和半圆形的韵律海岸形态Fig. 2 Consecutive V- shape and semi circular coast

图3 新型防波堤结构Fig. 3 New type of breakwater structure
本文从V式防波堤和离岸堤后形成稳定的类似V形和半圆形连续出现的韵律海岸地貌平面形态特点出发,对圆筒形防波堤进行改进和优化,提出一种前墙为连续半圆筒形的防波堤结构(如图3所示)。此种防波堤前墙形式相当于两个四分之一圆筒背靠背,后面为普通的沉箱结构。当两个防波堤结构拼接时又可以构成一个半圆筒的结构形式。此种防波堤具有圆筒形防波堤的优点,能使平行于防波堤轴线的波压力相互抵消,另外,其向外开口的弧形设置能有效引导波浪水流的流动,有效降低圆筒形防波堤在衔接处的波压力强度。
本文对该新型防波堤进行物理模型试验,获得了新型弧形防波堤在各种试验工况下,承受波浪力的大量数据,通过对数据进行分析总结,得出了新型弧形防波堤波浪力的分布规律和水平波浪力的计算方法,旨在为今后工程设计应用该防波堤结构形式提供科学依据。
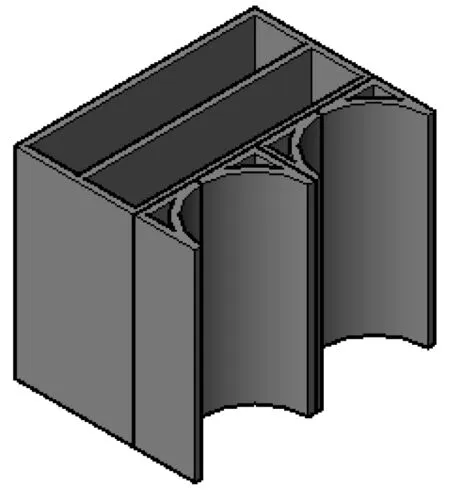
图4 新型弧形防波堤模型Fig. 4 Experiment model of the new breakwater
2 模型试验研究
2.1断面形式
由于此种形式防波堤没有工程应用资料,本次模型设计参考圆筒形防波堤的工程实例参数和圆筒形防波堤断面模型试验的方法,取防波堤中的一个单元和左右各半个单元组成模型的断面(如图4所示)。依据《波浪模型试验规程》JTJ/J234- 201中有关波浪模型试验的国内行业标准,本次试验中的物理模型采用正态模型,比尺为1∶20。模型高0.67 m,前段圆弧直径为0.4 m,后部沉箱宽0.4 m。试验过程中,沉箱内填充0.2 m高的块石,以保证模型的稳定。
2.2试验设备及仪器
试验在风-浪-流实验水槽内进行,水槽总长为45 m、宽0.8 m、深1.0 m,最低工作水深0.2 m,最高工作水深0.7 m。水槽的一端配有伺服电机驱动式造波机,在造波机后侧设有直立式消能网,水槽的另一端设有消能坡,以消除波浪反射影响。本次压强试验数据的测量和采集均使用成都泰斯特电子信息有限公司研制的CY200数字压力传感器测试系统,采集时间间隔为0.003 9 s。
模型试验时,取中间的四分之一圆弧面布置测点,共设3个测压断面,与来浪方向的夹角分别为0°、45°、75°,总计布置21个压力盒,用以测定水平波力沿防波堤环向和纵向的分布,波压力测点布置如图5所示。
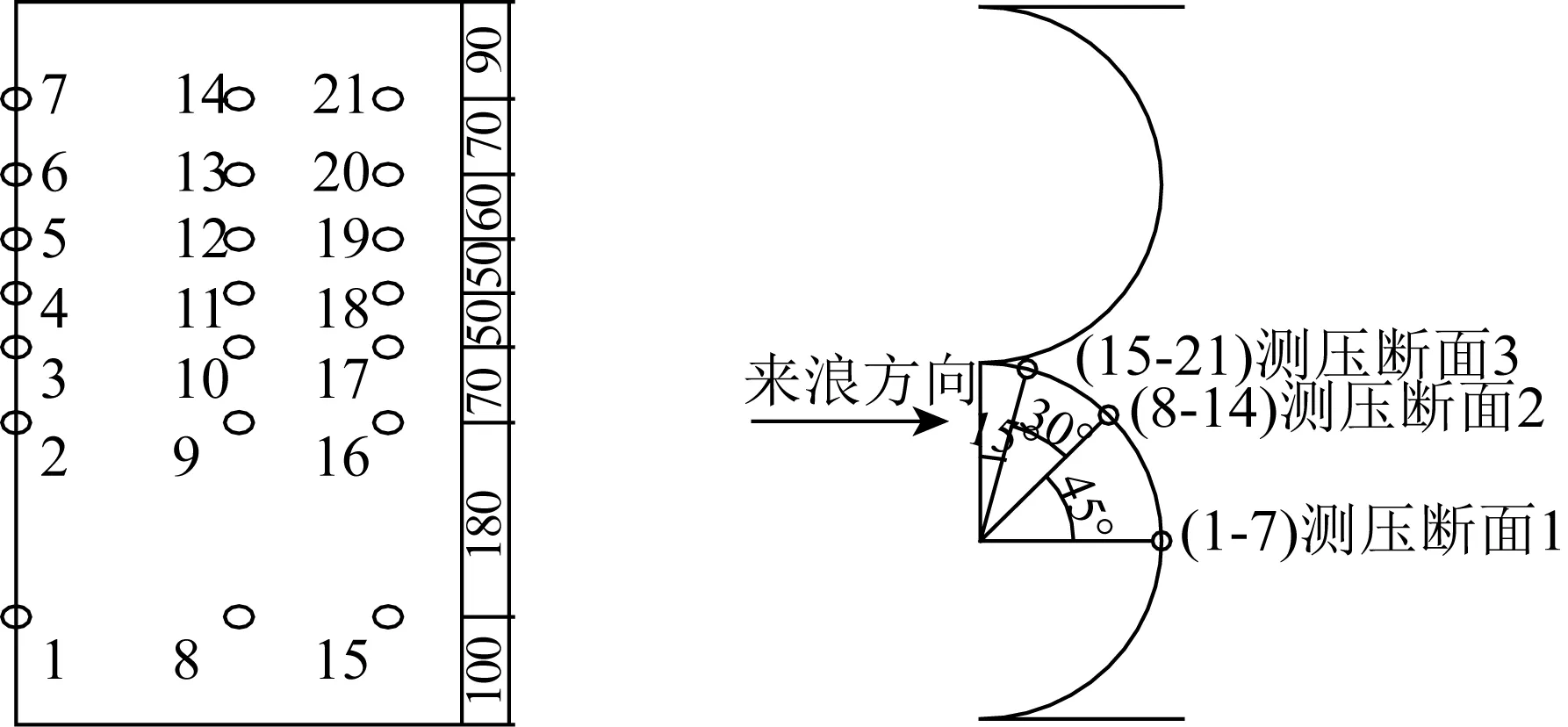
图5 弧形防波堤水平波压力测点布置Fig. 5 Arrangement of pressure sensors of the test model of curved breakwater
2.3试验参数
在三组不同水深情况下, 通过输入不同造波参数进行规则波造波,得到不同影响因素下防波堤所受波浪压力的大量数据。同一水深试验组次为20组,每组试验工况重复采集2次。
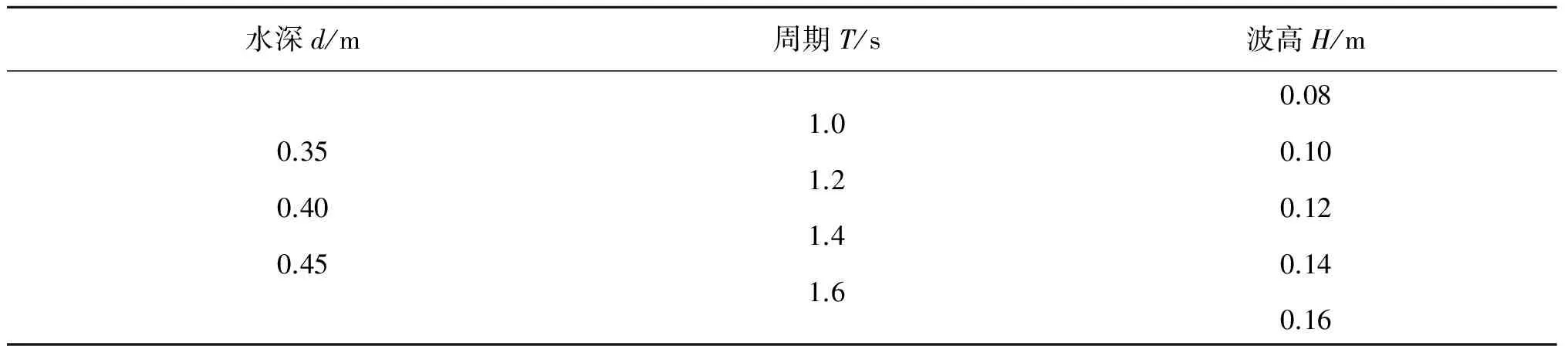
表1 试验水位及波浪要素Tab. 1 Test water levels and wave parameters
3 试验结果分析
3.1新型弧形防波堤波压力分布规律
波压力分布规律包括波压力垂向分布规律和波压力环向分布规律,由于此新型防波堤结构为直立堤式且其前墙形式与圆筒形防波堤类似,因此本文对其波压力分布规律的研究,借鉴了直墙和圆筒形防波堤的相关研究成果。
3.1.1 波压力垂向分布规律
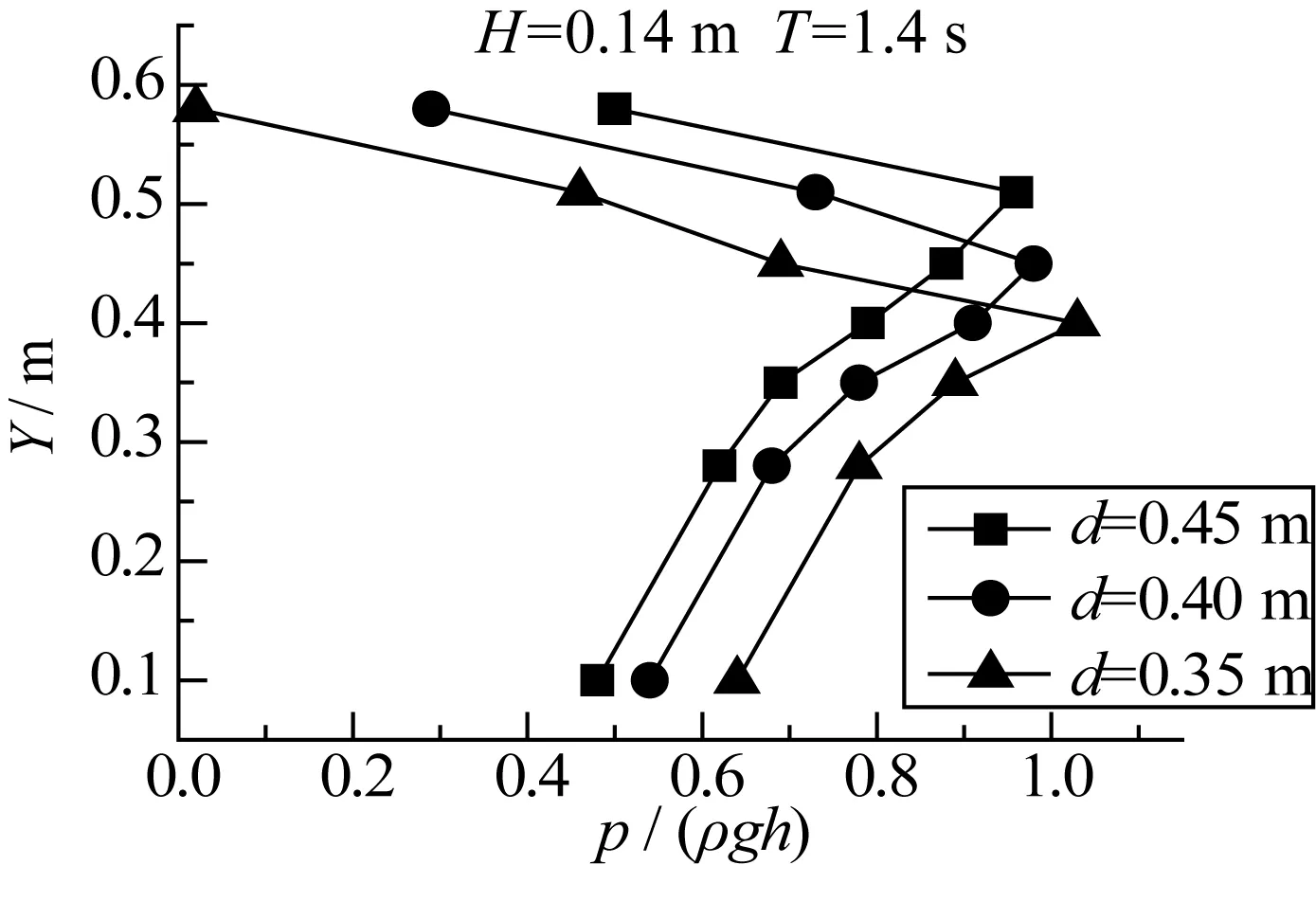
图6 相对压强垂向分布Fig. 6 The vertical distribution of relative wave pressure
在海港工程中,研究作用在建筑物上的波压力是经常要遇到的问题之一,为了得到波压力在建筑物上的作用力,必须知道压强沿水深的分布,本文研究的压强沿水深的分布为相对压强最大值沿水深的分布。目前大部分对直墙式建筑物波压力分布的研究都是以入射波高和水深作为控制参数,对其分布型式各家观点不尽一致。我国海港水文规范[4]认为对于不同的波态 (立波、近破波、远破波),应取不同的分布函数;合田良实[5]认为在静水位上下均服从线性分布;Minikin[6]认为动水压强在静水位上下服从抛物线分布;Kirkgoz[7]认为从墙体底部到静水位服从抛物线分布,而从静水位到水面上1.6d处服从线性分布, 其中d为直墙上发生最大冲击时的墙前水深。对于圆筒形防波堤波压力沿水深的分布,也有很多学者做过研究,如苏联的O.H.凡恰戈夫[8],中国海洋大学的夏运强[9]以及钟声杨[10]、柳玉良[11]、葛蓉[12]等。普遍的结论是:圆筒形防波堤波压力沿水深的分布与直立堤具有大致相同的趋势。图6为新型弧形面防波堤在波高H=0.14 m,周期T=1.4 s,不同水深情况下测压断面1的相对压强沿垂向的分布图。(Y代表距沉箱底部的距离,P/(ρgh)代表相对压强)
对图6以及对多种试验工况下得到的压力值垂向分布趋势进行充分分析后可以得出新型弧形防波堤波压力垂向分布情况:最大波压力出现在静水位附近,静水位以上近似符合三角形分布,静水位以下近似抛物线分布。与Kirkgoz[7]及葛蓉[12]的观点比较一致。
3.1.2 波压力环向分布规律
对于圆筒形防波堤波压力环向分布情况,钟声扬[10]通过对削角圆沉箱防波堤进行波压力试验,得出圆筒波压力环向分布为:圆筒沉箱左右两侧受压对称, 横截面上正负压强的最大值,几乎都发生在偏于正波向左右40°附近,而并非在左右死角80°处。柳玉良[11]通过在波浪水槽对顶部有反弧形胸墙的圆沉箱防波堤进行断面模型试验,波压力测点环向布置与来浪方向夹角分布为0°、18°、36°、54°、72°方向,通过实验测得圆沉箱同一高程各点承受平行于波浪方向的水平力,沿圆弧随角度的增大而减少。对于多个圆筒连续布置的情况,苏联的O.H.凡恰戈夫[8]认为,在同一深度处圆筒半圆顶处的波压强小而相邻凹入部分逐渐增大。夏运强和陈兆林[9]等人进行了圆沉箱波浪力的模型实验,分别给出了在波峰和波谷作用下圆沉箱上环向波压强的分布趋势:波峰作用时,正面与侧面波压强大小基本相同;波谷作用时,在某一深度以下,侧向波吸力变大,甚至大于同深度处的波峰时波压强。

图7 波峰作用时环向压强分布Fig. 7 Distribution of circumferential wave pressure during wave crest
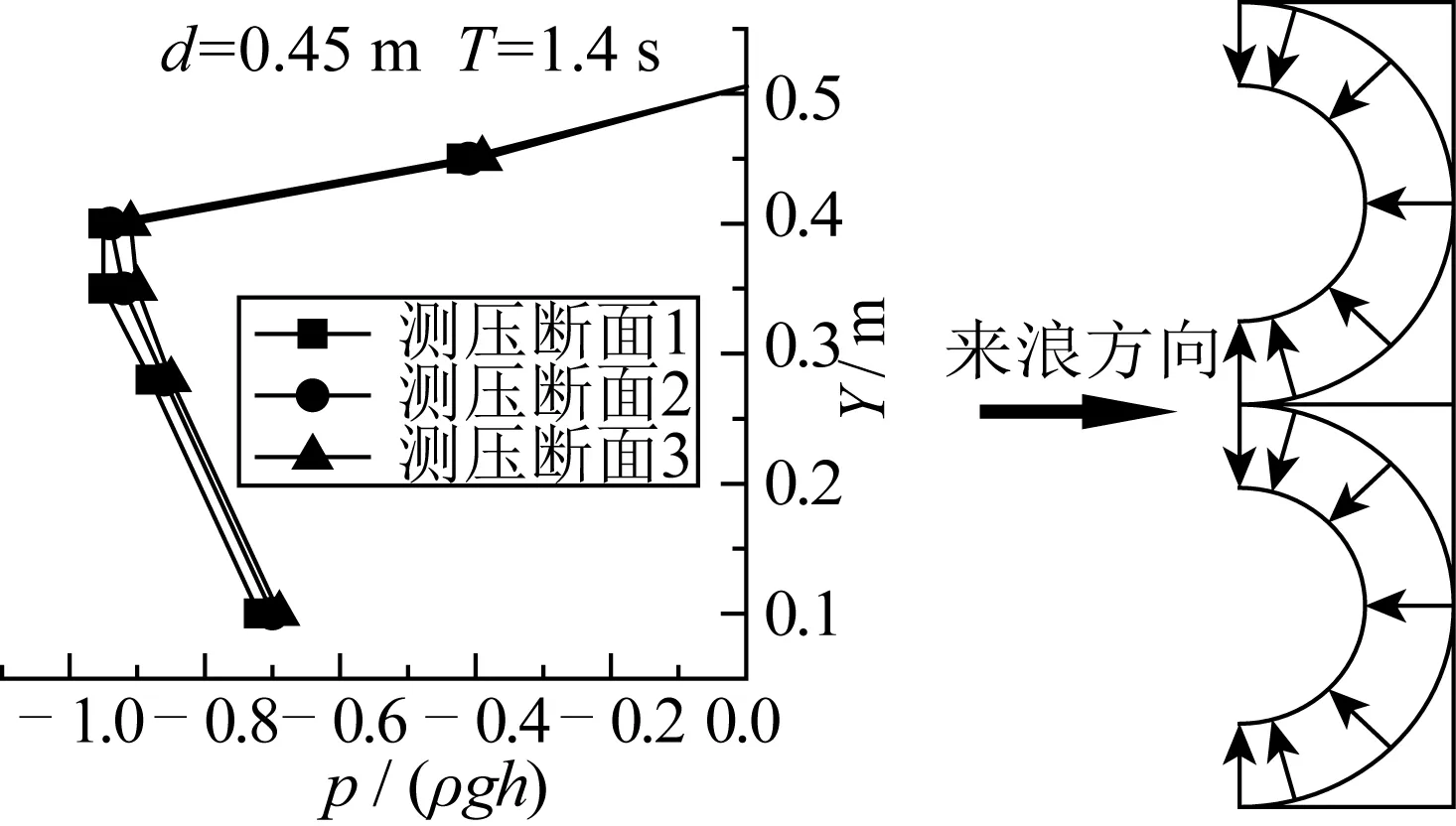
图8 波谷作用时环向压强分布Fig. 8 Distribution of circumferential wave pressure during wave hollow
图7和图 8分别为波峰和波谷作用时,新型弧形防波堤不同测压断面的波压力分布。从中可以看出,波峰作用时,同一高程下,波压力的大小为:测压断面1>测压断面2>测压断面3,即正面波压强最大,沿圆弧随角度增大而减少。但总体来看,各测压断面环向压力差值并不大,不超过12%,并没有出现像圆筒形防波堤那样在防波堤衔接处呈显著的增大现象。相比较而言,新型弧形防波堤受力状态更好。波谷作用时,同一高程下,各测压断面的波压力基本相等,即沿圆弧均匀分布。
3.2新型弧形防波堤波压力影响因素分析
3.2.1 波高的影响
图9(a)~9(c)为水深0.45 m,周期1.4 s,波高分别为0.08、0.10、0.12、0.14、0.16 m时,各测压断面上各测点波压力分布。由图可知,弧形防波堤上各测点的相对压强随波高的增大而增大。
3.2.2 周期的影响
图10(a)~10(c)为水深0.45 m,波高0.14 m,波周期分别为T=1.0、1.2、1.4、1.6 s时,各测压断面上不同测点的波压力分布。弧形防波堤上的各测点相对压强随周期的增大而增大,说明长波的波压力较大。
3.2.3 水深的影响
从图6波高、周期相同,水深不同时的垂向波压力分布图可以看出,随着水位的降低,静水位以上测点波压强随之减少,静水位以下各测点波压强随之增大。这是由于波浪的能量汇集区在静水位附近,随着水位的降低,能量汇集区域逐渐下移,水位以下各测点所受波动作用更为显著。
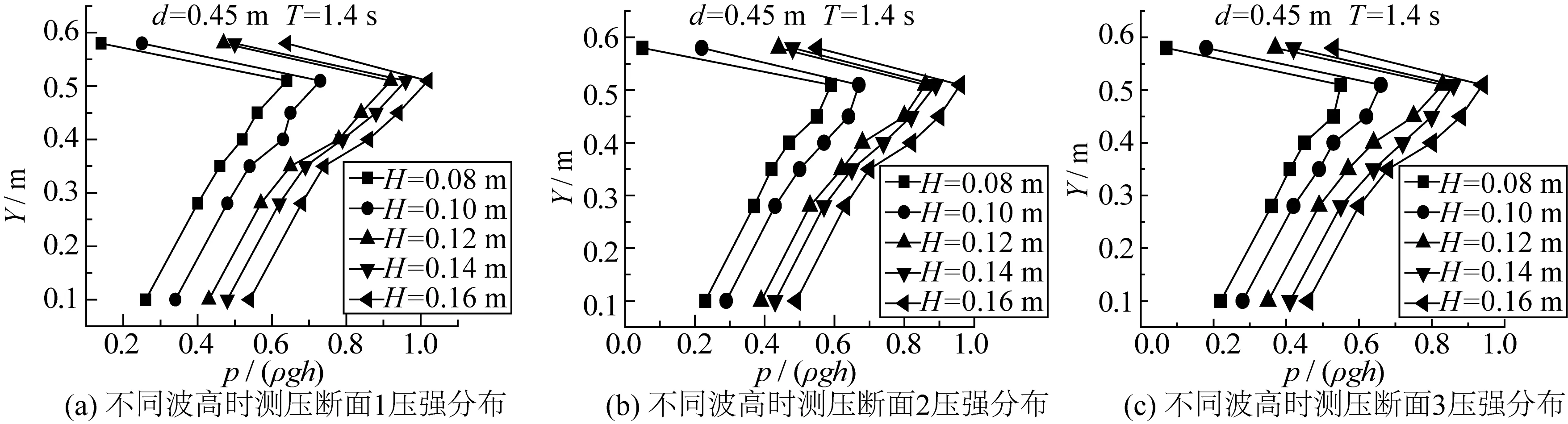
图9 不同波高时各测压断面的波压强分布Fig. 9 Pressure distribution of different measuring sections under different wave heights

图10 不同周期时各测压断面上的波压强分布Fig. 10 Pressure distribution of different measuring sections under different wave periods
3.3新型弧形防波堤与矩形沉箱波压力的比较
将波压力试验值分别与合田良实公式和海港水文规范公式进行比较分析(图11)。分析可知,最大波压力测点在静水位偏上5 cm处,最大波压力以上的测点压力实测值与海港水文规范和合田良实公式较为接近。静水位以下各测点波压力值普遍少于海港水文规范和合田良实公式理论值。且各测点与海港水文公式相差较大,为30%~40%。与合田良实公式比较,误差为8%~20%。相比较而言合田良实公式比较接近实测值。这是由于合田良实公式考虑了不完全反射,这符合试验观察到的不完全立波波态的现象。总体来看,弧形防波堤各断面波压力明显小于矩形沉箱波压力。

图11 波浪总水平力试验值与各家理论公式的比较Fig. 11 Comparison of different theoretical methods of wave forces and experimental results
3.4新型弧形防波堤所受水平总力分析
波浪力的研究通常分为三方面:一是理论研究,二是物理模型实验,三是数值模拟。理论研究作为物理模型实验和数值模拟的基础,可以为这两方面提供坚实的理论依据。MacCamy和Fuchs[13]于1954年得到了大直径圆柱体的线性绕射解析解,此后Hutington[14]和Raman[15]等学者基于此理论对圆柱体上的波浪荷载进行了研究。但由于圆沉箱结构的特殊性,影响因素众多,理论研究过程中进行了大量假设,公式推导复杂,实际应用性不强。目前大多数研究者采用的是基于物理模型试验的经验公式法,即在实验室内的水槽(水池)内对大圆筒模型在各种水深、周期、波高下的波浪力进行测试,然后用统计分析的办法确定经验公式中的经验系数。如苏联的O.H.凡恰戈夫[8]、天津大学张子樵[16]、夏运强[9]、柳玉良[11]、葛蓉[12]等。本文研究也采用类似方法。由试验数据分析可知,弧形防波堤上的波压力与合田良实公式计算值比较接近。因此,在合田良实公式的基础上,考虑修正系数,提出计算新型弧形防波堤波压力的计算公式:
P=KpPz

图12 拟合公式得到的计算值与实测值的对比Fig. 12 Comparison of values obtained by fitting formula and measured values
式中:Kp为修正系数,P和Pz分别为作用在弧形防波堤和合田良实直墙式的水平波浪力。
将试验值沿圆弧面积分(1/4圆弧面)并将其沿水平方向分解得到作用在弧形防波堤的总水平波浪力,表2为弧形防波堤总水平波浪力与合田良实公式计算值的比较。由表可知,取修正系数=0.91。
为验证修正系数Kp选取的可靠性,本文将在各工况下按拟合公式计算得到的波浪水平总力计算值与实测值进行对比,如图12所示。图中Y轴为按拟合公式得到的计算值,X轴为实测值。由图可知,数据点均匀分布于y=x的两侧,说明修正系数选取较为准确可靠。

表2 水平总力实测值与合田良实公式比较Tab. 2 Comparison of Goda fomula of horizontal total force and measured values
4 结 语
通过对前墙形式为连续半圆形的新型弧形防波堤进行规则波作用下的物理模型试验,研究了此种新型防波堤波压力的分布规律及其影响因素。通过将试验结果与海港水文规范和合田良实公式进行比较分析,提出了计算新型防波堤总水平波浪力的方法。试验分析结果表明:
1)弧形防波堤波压力垂向分布与直墙式防波堤类似,静水位附近为三角形分布,静水位以下为抛物线分布;弧形防波堤波压力环向分布为:波峰作用时,与波浪入射角相同的断面波压强最大,沿圆弧角度的增大,波压强减少;波谷作用时,波压强基本相等,呈均匀分布。值得指出的是,即便在波峰作用时,波压强沿断面分布不同,但其相差并不大,受力状态比圆筒形防波堤要好。
2)弧形防波堤波压强随波高、周期的增大而增大。
3)弧形防波堤总水平波浪力计算宜采用修正后的合田良实公式,计算分析表明,弧形防波堤水平波浪总力比同等尺度直墙式防波堤的波浪力小10%左右。
由于波浪与圆筒作用十分复杂,本次只是在物理模型试验的基础上对新型防波堤进行的初步研究,试验波况均为正向且不越浪,没有进行垂向波浪力研究,也没有考虑防波堤上部胸墙的影响,对防波堤水平波浪总力是通过波压力测点积分得到,有待以后进一步试验验证。建议在波浪水池里对此种弧形防波堤进行足尺试验,并和同尺度直立堤进行对比,对波浪斜向入射情况和波陡、相对水深、相对筒径、相对波高等影响波压力的因素进行深入研究。
[1] 周锡礽,王晖,韩桂军. 大直径薄壳圆筒结构的设计与计算[J].港工技术,1995,2:22- 30. (ZHOU Xireng, WANG Hui, HAN Guijun.Design and calculation of the large- diameter cylinder shell structure[J]. Port Engineering Technology,1995,2:22- 30(in Chinese))
[2] 程建生,缪国平,尤云祥,等.波浪在V形贯底式防波堤上绕射的解析研究[J].上海交通大学学报,2005,39(5):813- 816. (CHENG Jiansheng, MIAO Guoping, YOU Yunxiang, et al. Analytical research on the wave diffraction on V- type bottom- mounted breakwaters[J]. Journal of ShangHai Jiao Tong University,2005,39(5):813- 816.(in Chinese))
[3] Analytical and numerical models of the RIBSXM99 ocean- scale prototype[R]. Washington, DC: US Army Corps of Engineers, 2009.
[4] TJ/T 213- 1998. 海港水文规范[S]. 北京:人民交通出版社,1998,52- 104. (TJ/T 213- 1998. Code of hydrology for sea harbour[S]. Beijing: People's Communication Press,1998,52- 104.( in Chinese))
[5] GODA Y. Random seas and design of maritime structures[M].Tokyo:Tokyo Press,1985:107- 144.
[6] MINIKIN R R. Wind waves and maritime structures [M].1950:2- 36.
[7] KIRKGOZ M S.Influence of water depth on the breaking wave impact on vertical and sloping walls[J]. Coastal Eng., 1992, 18:297- 314.
[8] KASCACHEK G D,Wanzakov O M.Interaction between regular wave and circular breakwaters[J].ASCE,1971.
[9] 夏运强,陈兆林.圆筒形水工建筑物波浪荷载的试验研究[J].海洋工程,2002,20(3):81- 86. (XIA Yunqiang,CHEN Zhaolin. Experimental study of wave forces on the surface of cylinder structures[J].The Ocean Engineering,2002,20(3):81- 86.(in Chinese))
[10] 钟声杨.削角圆筒防波堤的波压力试验[J].水利水运科学研究,1980,4:104- 106. (ZHONG Shengyang. Experimental study of wave pressure on the surface of chamfered cylinder breakwaters[J].Hydro- Science and Engineering,1980,4:104- 106. (in Chinese))
[11] 柳玉良,杨洪旗, 王爱群,等.圆形沉箱防波堤波压力的试验分析[J].海岸工程,2004(23):8- 15. (LIU Yuliang,YANG Hongqi, WANG Aiqun, et al. Test and analysis of wave pressure on circular caission breakwater[J]. Coastal Engineering,2004(23):8- 15. (in Chinese))
[12] 葛蓉,陈国平,严士常. 圆沉箱护岸结构波浪力试验研究[J].水运工程,2013,9(483):31- 35. (GE Rong, CHEN Guoping, YAN Shichang. Experimental study on wave forces on circular caission revetment[J].Port and Waterway Engineering, 2013,9(483):31- 35. (in Chinese))
[13] MACCAMY R C,FUCHS R A.Wave forces on piles:a diffraction theory[Z]. Tech. Memo. No.69. US Army Coastal Engineering Research Center,1954.
[14] HUTINGTON S W. Wave loading on large cylinders in short crested seas [A]//SHAW. TL, Mechanics of Wave Induced Forces on Cylinders[R]. London:Pitam,1979: 636- 649.
[15] RAMAN H, Sambhu Venkata Rao P. Dynamic pressure distribution on large circular cylinders caused by wind generated random waves[J]. Ocean Engineering ,1983,10(4):235- 260.
[16] 张子樵. 圆筒防波堤立波波压力试验研究[J].天津大学学报,1991(S):103- 108. (ZHANG Ziqiao. Experimental studies on standing wave forces on circular cylinder breakwaters[J]. 1991(S):103- 108. (in Chinese))
Experimental study on wave forces on curved breakwater
ZHAO Liping1,2, ZHU Yazhou1,2, XIE Aoyun1,2, ZOU Junfei1,2
(1. School of Hydraulic Engineering, Changsha University of Science & Technology, Changsha 410007, China; 2. Key Laboratory of Water & Sediment Science and Water Hazard Prevention, Changsha 410004, China)
Based on the circular cylinder breakwater and the V- shaped breakwater, considering the coastal geomorphic plane morphology characteristics that consecutive V- shape and semi circular coast would be formed behind the offshore breakwater, a form of breakwater is proposed with a semi- cylindrical continuous front wall. Through the regular wave model experiment in a wave flume, the wave force distribution and the influence factors for wave forces on this new breakwater are studied, such as wave height, period, water depth, etc. The results are compared with theoretical values according to the Seaport hydrology standard formula and the Goda formula, and the modified Goda is given for total horizontal wave force on this new breakwater. The results show that the wave pressure on curved breakwater increases with the incease of wave height and wave period, and that the total horizontal wave forceis less than that of the same scale vertical breakwater by about 10%.
circular cylinder breakwater; V- shaped breakwater; semi- cylindrical; force distribution; total force
TV32
A
10.16483/j.issn.1005- 9865.2015.05.005
1005- 9865(2015)05- 035- 07
2015- 01- 20
国家自然科学基金资助项目(51109018)
赵利平(1961- ),男,浙江义乌人,教授,博士生导师,主要从事波浪水流与结构相互作用研究。E- mail:zhaolp@csust.edu.cn
