销售努力和风险厌恶下供应链的回购契约
2015-10-26代建生孟卫东
代建生,孟卫东
(重庆大学经济与工商管理学院,重庆400030)
销售努力和风险厌恶下供应链的回购契约
代建生,孟卫东
(重庆大学经济与工商管理学院,重庆400030)
运用CVaR方法研究了风险厌恶销售商实施促销努力下回购契约的协调问题.讨论了销售商的最优订购和促销决策,并分析了促销行为和风险厌恶对订购决策的影响.考察了两类回购与成本分担契约的渠道协调问题:一种有单边转移支付,一种无单边转移支付,研究表明:如果销售商非常厌恶风险(风险厌恶系数小于临界值),两种契约都不能协调供应链;否则,两者在市场需求信息对称下均能完成渠道协调,但只有前者在需求信息不对称下能够协调供应链.最后用数值分析考察了有效契约可行域、契约参数关系、以及渠道利润的分配.
供应链;回购契约;销售努力;风险厌恶
1 引 言
在供应链合约实践中,当产品的销售期比较短暂且市场需求不确定时,供应商往往采用回购契约来补偿零售商,引导零售商增大订购量.通过回购契约,因需求不确定产生的风险由供应商和零售商共同承担.回购契约常应用于易逝品销售渠道,如时尚用品市场、图书销售、化妆品专营等.
已有大量文献对回购契约的可协调性进行了研究[1−6].比如,文献[1]指出供应商采取的最优回购策略是允许销售商对剩余订货全部按批发价退货.文献[2]研究了一般的回购契约、基于差别定价的回购契约和销售回扣契约等三类回购契约,指出只有基于差别定价的回购契约可协调供应链.文献[5]表明回购契约将导致对零售商的过度激励,并提出利用数量折扣契约机制来修正回购契约.
上述研究都没有考虑销售努力对回购契约协调供应链的影响,而渠道成员的促销努力将影响市场对商品的需求[7],从而影响销售商的订购决策,并可能导致渠道协调不能实现[8].文献[8–12]考察了存在促销努力下回购契约的协调问题,他们的研究都表明对回购契约加以改进能够协调此类供应链.比如,文献[9]表明销售回扣契约和回购契约的组合可实现渠道协调.文献[10,11]提出了多个能协调具有促销努力供应链的回购契约安排.
上述研究都假定渠道成员风险中性,而近期的一些研究表明决策者的行为往往表现出某种风险厌恶的特性[13].风险厌恶的决策者在策略选择上更为保守,文献[14,15]研究指出:相对于风险中性者,风险厌恶的销售商趋向于更低的订购水平.当供应链的渠道成员厌恶风险时,上面提到的能完成渠道协调的契约安排或其组合还有效吗?文献[16–18]对此问题进行了研究,结论是回购契约并不能协调所有风险厌恶的供应链.文献[19]运用CVaR方法也讨论了这一问题,指出当销售商不是过于厌恶风险时,回购契约能够协调供应链.文献[20]提出了风险厌恶下协调供应链的帕累托有效标准,并在期望效用方法和均方分析方法下给出了能协调供应链的回购契约满足的条件.但文献[16–20]都没有探讨销售努力行为对契约协调的影响.
本文将在销售商风险厌恶且实施促销努力影响市场需求下考察供应链的契约协调问题,两种回购与成本分担契约被讨论:一种有单边转移支付,一种无单边转移支付.在销售商知晓市场需求分布信息且不过于厌恶风险下,研究表明:如果需求信息对称,两者均能协调供应链;如果需求信息不对称,前者能完成渠道协调但后者不能,这与销售商风险中性情形有所不同.在销售商风险中性下,无论市场需求信息对称与否,两者均能协调供应链,这是本文在理论上的主要边际贡献.
在分析技术上,由于测度风险的条件风险价值(CVaR)方法具有良好的结构和计算特性,且与二阶随机占优及高阶随机占优保持一致性[21,22],本文将采用这一方法来评价风险厌恶销售商的风险价值.
2 模型描述、基本假设和符号说明
考虑由供应商和销售商构成的双层供应链,该供应链经营报童类商品.商品的边际生产成本c及市场价格p是外生给定的,其市场需求是不确定的,用连续随机变量ξ来表示,06ξ6U,其分布函数和密度函数分别记为F(·)和f(·).销售商不清楚市场的最终需求,但知道其概率分布.
销售商的促销努力e能影响商品的市场需求,e越大,潜在的市场需求越大.将商品需求与销售努力的关系模型化为乘法关系eξ,其中e>1[9,10].销售努力必须在商品销售实现前进行,比如广告.销售努力给销售商带来的成本为C(e),成本函数C(·)关于e严格凸增、二阶可导,且C(1)=0,C′(1)=0.
销售商只有一次订购机会,设其订购量为y.如果市场需求小于这个订购量,需求得到满足,但剩余商品没有残余价值;如果市场需求大于这个订购量将不能得到满足,最终实现的销售量为min{y,eξ},但过度需求不会给供应链带来其它损失.
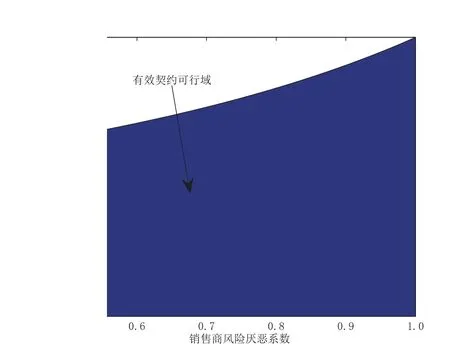
为了激励销售商增大订购量,供应商与销售商达成以下回购契约(w,b):供应商按批发价格w向销售商供给商品,并按每单位b的价格回购剩余商品,为了避免订货过度,要求b 此外,本文的研究基于以下假设: 假设1 供应商是风险中性的,销售商是风险规避的,其风险价值由CVaR方法来度量. 假设2 供应商是斯塔伯格领导者,设定回购契约;销售商是跟随者,确定订购和促销决策. 假设3 供应商知晓销售商的风险规避程度. 假设4 供应商和销售商的保留收益均为0. 给定回购契约(w,b),在策略组合(y,e)下,供应商和销售商的利润函数分别记为πS(y,e)和πR(y,e) 其中(x)+=max{x,0}. 在CVaR标准下,销售商的风险价值为[23] 其中E是期望算子,η∈(0,1]是对销售商风险厌恶程度的度量,η越小,销售商风险厌恶程度越大;η=1对应着销售商风险中性的情形. 分别用上标I、b和ϕ表示集权式决策系统、回购契约(w,b)下的分权式决策系统和回购与成本分担契约(w,b,ϕ)下的分权式决策系统;用下标SC、S和R分别表示供应链、供应商和销售商. 3.1 集权供应链的决策分析 根据式(1)和式(2),供应链整体的利润为 集权供应链面临的问题是:选择最优订购量和销售努力,实现渠道期望收益的最大化,即 EπSC(y,e)关于y,e是联合凹的,最优订购量yI∗和销售努力eI∗满足以下一阶条件 定义1 订购的商品不能实现完全销售的概率,称之为余货概率.订购的商品不能满足市场最终需求的概率,称之为缺货概率. 3.2 分权供应链的决策分析 在分散决策系统下,风险厌恶的销售商从策略可行集中选择最优策略来最大化自身风险价值(P1) 进而有 引理1 在P1中,g(v,y,e)关于v是单峰的,极大点为v∗(y,e)=(p−w)y−C(e). 引理1指出v∗(y,e)=(p−w)y−C(e),将其置入式(8),有 命题1 在CVaR标准下,销售商的最优订购量和最优销售努力满足以下一阶条件 销售商的订购决策是基于分权系统最优余货概率进行的,但在CVaR风险度量准则下,销售商仅在期望意义上最大化低于η分位数的那部分收益水平.订购的最后一单位商品如能实现销售,给销售商带来的边际净收益为p−w,实现销售的主观概率为η−r;但如果出现余货,在回购契约下的机会成本为w−b,概率为r.根据边际收益等于边际成本的原则,有(p−w)(η−r)=(w−b)r,它与式(10)等价. 3.3 销售努力和风险厌恶对订购决策的影响分析 命题2 无论是集权决策系统还是分权决策系统,销售商的促销努力都增大了最优订购量. 证明:略. 命题3 在分权供应链中,最优订购量和销售努力随销售商风险厌恶程度的上升而减小. 销售商的风险厌恶通过两条途径对最优订购量产生影响:一是直接改变最优余货概率,二是改变最优销售努力.重写式(10)如下:yb∗=eb∗F−1(r),当销售商更加厌恶风险时,最优销售努力和余货概率均减小,因而订购量减小.命题2和命题3联合表明,销售努力和风险厌恶都将影响其订购决策,从而对协调供应链的契约安排产生影响. 4.1 回购契约(w,b,ϕ)的协调问题 在回购契约(w,b)的基础上,由供应商分摊销售商部分促销成本,并设其分担比例为1−ϕ,后文提及为契约(w,b,ϕ).为了确保对销售商的促销激励,规定ϕ>0.在该契约下,销售商的利润函数为 销售商的最优订购量和销售努力满足以下一阶条件 比较式(5)、式(6)和式(12)、式(13)可以发现,要实现渠道协调,需要求 式(14)和式(15)包含三个内生变量,而只有两个方程,故其解有一个自由度.为了表述的方便,选择ϕ作为自由变量.对任意ϕ∈(0,1],联立求解式(14)和式(15),得 定义2 所有形如(w∗(ϕ),b∗(ϕ),ϕ)的契约,其中ϕ∈(0,1],w∗(ϕ)和b∗(ϕ)分别满足式(16)和式(17),称之为激励相容的回购契约. 由式(16)和式(17),将w∗(ϕ)和b∗(ϕ)分别对ϕ和η求偏导,可得下列结论. 命题4 在激励相容契约安排中,批发价格和回购价格随销售商成本分担比例增大而减小,且回购价格减小的速度更快;w∗(ϕ)与η无关,而b∗(ϕ)随η的上升而下降. 在激励相容契约(w∗(ϕ),b∗(ϕ),ϕ)中,b∗(ϕ)是η的减函数,销售商越是风险厌恶的,完成渠道协调的回购价格就应定得越高,销售商承担的需求波动风险就越小.但奇怪的是w∗(ϕ)与η无关,这与直觉相违背,因为w∗(ϕ)的大小会影响销售商的促销策略并最终影响其收益.w∗(ϕ)越小,销售商就越有激励去增大销售努力,反之亦然.运用式(14)重写式(13),有 注意到上式右侧不含变量η,且要使渠道实现协调,有eϕ∗=eI∗,因而w∗(ϕ)与η无关. 命题4表明对风险厌恶程度不同的销售商,可以制定统一的批发价格,但应设定不同的回购价格.而且销售商越厌恶风险,与之对应的回购价格就越高. 供应链及其成员在契约(w∗(ϕ),b∗(ϕ),ϕ)下的利润可表示为 销售商的风险价值为 其中E[yI∗−eI∗ξ,0]+是最优余货的期望值,而pE[yI∗−eI∗ξ,0]+是最优余货的期望市场价值. 比较式(19)和式(21)可知,式(19)中的第二项是为激励销售商采取最优订购和促销策略,供应商提供给销售商的额外风险补偿.特别地,当η=1,风险补偿价值为零. 命题5 在激励相容契约(w∗(ϕ),b∗(ϕ),ϕ)下,有下列结论:1)销售商分得的利润占比不小于ϕ,且随其成本分担比例和风险厌恶程度的增加而增大;供应商分得的利润占比不大于1−ϕ,且随销售商成本分担比例和风险厌恶程度的增加而下降.2)销售商的CVaR与成本分担比例成正比,与风险厌恶程度无关. 定义3 如果在某契约下所有渠道成员的收益不小于保留收益,则称该契约满足参与约束. 如果EπS(y,e)|w,b,ϕ>0且CVaRη(πR(y,e))|w,b,ϕ>0,那么(w,b,ϕ)满足参与约束. 定义4 所有满足参与约束且w>b的激励相容契约(w∗(ϕ),b∗(ϕ),ϕ)称之为有效契约. 根据定义4,所有能够协调供应链的回购契约都是有效契约.反之,有效契约能够完美协调供应链,既然它能最大化渠道利润,满足参与约束及条件w>b. 定理1表明只有当销售商不过于厌恶风险时,才存在能协调供应链的回购契约.在CVaR下,风险厌恶系数的临界值就是集权系统最优余货概率. 由式(19)和式(20)可知,风险补偿价值ϕ(1−η)pE[yI∗−eI∗ξ,0]+的大小不仅依赖于销售商的风险厌恶程度η,还依赖于市场需求分布信息F(·).因此,当销售商风险厌恶时,要判定一个契约安排是否有效,供应商必须了解市场需求的分布信息,并从中确定风险补偿价值的大小.这与销售商风险中性的情形明显不同.在销售商风险中性下,销售商是期望利润极大化者,只有市场需求的期望会影响销售商的收益,而需求的波动对其没有影响,在这种情形下,供应商不必对销售商的风险损失进行补偿,既然销售商不存在风险损失,供应商也就不必关注市场需求的分布信息. 如果供应商不知晓需求分布信息且销售商严格风险厌恶,所有激励相容契约(w∗(ϕ),b∗(ϕ),ϕ)都是无效的. 注意到b∗(ϕ)=(1−ηϕ)p,不等式(22)的左侧表示供应商回购商品余货需要支付的货币总额,而右侧是供应商从商品销售中分享的利润,这个不等式的意义是显然的. 4.2 回购契约(w,b,ϕ,t)的协调问题 前面分析表明要使回购契约更有效率,需要从供应商的信息不完美入手,解决办法之一是在回购契约(w,b,ϕ)的基础上,通过单边转移支付来确保供应商的参与约束得到满足,且转移支付的具体大小在事后通过谈判达成,从而消除信息不对称导致的问题.将带有转移支付的回购与成本分担契约记为(w,b,ϕ,t).由于转移支付没有激励效应,前面关于契约(w,b,ϕ)的讨论也适用于(w,b,ϕ,t),唯一不同的是需将式(19)、(20)和(21)修改为含有固定转移支付项. 定理3 当销售商风险厌恶系数小于集权系统最优余货概率时,不存在有效的回购契约(w,b,ϕ,t);当销售商风险厌恶系数大于集权系统最优余货概率时,一切激励相容的契约(w∗(ϕ),b∗(ϕ),ϕ,t)都是有效的. 在有效契约(w∗(ϕ),b∗(ϕ),ϕ,t)中,前三个变量的组合使得销售商的订购和促销决策实现了帕累托意义上的最优,而最后一个变量确保了渠道成员的参与激励,从而达到协调供应链的目的.特别地,前三个变量是事前确定的,而t是事后通过谈判确定的. 在信息不对称下,即使销售商不过于厌恶风险,无单边转移支付的回购契约也不能协调供应链,而有单边转移支付的回购契约则能完成渠道协调,这表明固定转移支付也具有一定的协调功能.在批发价格给定的情形下,调增回购价格能诱导销售商增大订购量,以至选择系统最优的订购量,但这一政策调整将减小供应商的利润,通过单边转移支付则可确保供应商获得某一确定的利润水平.上述讨论引出的管理洞见是:通过销售商向供应商转移固定支付,增大了供应商调整回购价格的范围,从而有助于完成渠道协调.这一合约实践已运用于图书及化妆品连锁经营模式中,其中加盟店(销售商)向总部(供应商)支付的加盟费和管理费等在本质就是固定转移支付. 由于刻度选择问题,市场价格和生产成本绝对数据的大小无关紧要,其相对大小(生产成本与市场价格之比)更为重要.尽管不同商品的生产成本与市场价格之比的差异较大,但多数集中在30%~70%之间.不损一般性,在数值分析中假定p=2,c=1.ξ服从均匀分布U(1,100),C(e)=50(e−1)2. 给定参数值p=2,c=1,由定理2可知,只有当η>0.5时,才存在能协调供应链的回购契约安排.定理2还表明,即使在信息对称下,有效契约(w,b,ϕ)的可行域也受到很大的限制,其中销售商风险厌恶程度对契约可行域有重要影响.图1模拟了不同η值下ϕ的取值范围.当η60.5时,不存在可行的契约(w,b,ϕ)能协调供应链.当η=1时,任意契约(w∗(ϕ),b∗(ϕ),ϕ),其中ϕ∈(0,1],都可协调供应链. 定理3表明,在契约(w,b,ϕ,t)下,总存在t,使得对任意ϕ∈(0,1],契约(w∗(ϕ),b∗(ϕ),ϕ,t)可协调供应链.在参数值η=0.7下,图2模拟了激励相容契约(有效契约)中批发价格与回购价格随销售商成本分担比例的变化情况:回购价格和批发价格都随销售商成本分担比例的上升而下降,且回购价格下降速度更快.不同于契约(w,b,ϕ,t),在契约(w,b,ϕ)下,并非所有激励相容的契约都是有效的.图2中AB线的左侧反映了信息完美下所有的有效契约(w∗(ϕ),b∗(ϕ),ϕ),其右侧的契约尽管也是激励相容的,但不满足供应商的参与约束. 图1 信息对称下有效契约的可行域Fig.1 Feasible domain of effcient contracts under symmetric information of demand 图2 激励相容契约参数之间的相互关系Fig.2 The relationships among parameters of incentive compatible contracts 在图2所示的有效契约中,不同契约安排下渠道成员所得利润是不同的,最终采用的契约将通过谈判达成.图3在参数η=0.7下模拟了不同契约(w∗(ϕ),b∗(ϕ),ϕ)下供应链整体及其成员的期望利润.从图3可知,存在销售努力下的渠道总利润大于无销售努力下的渠道利润;供应商的利润随ϕ的上升而减小,销售商的利润随ϕ的上升而增大;当ϕ>0.75时,供应商的期望利润小于零,与之对应的契约是不可行的. 图3 有效契约下供应链及其成员的期望利润Fig.3 The expected proft of the supply chain and channel members under effcient contracts 在销售商风险厌恶且其销售努力影响市场需求的背景下,假定销售商知晓市场需求的分布信息,运用CVaR方法研究了回购契约的协调问题.将最大化供应链利润的订购量出现剩余的概率定义为集权系统最优余货概率,并将能够协调供应链的回购契约称之为有效契约,研究指出有效契约必须同时满足激励相容和参与约束条件.通过研究得到以下结论:当销售商的风险厌恶系数小于集权系统最优余货概率时,不存在有效的回购与成本分担契约.当销售商的风险厌恶系数大于集权系统最优余货概率时,如果供应商也清楚市场需求的分布信息,回购契约能够协调供应链;否则,需要借助单边转移支付机制,回购与成本分担契约才能完成渠道协调.这与销售商风险中性的情形明显不同,在销售商风险中性下,无论市场需求信息对称与否,回购与成本分担契约均能协调供应链,而不必借助其它协调机制. 研究揭示了以下管理启示:第一、针对不同的销售商,供应商可制定统一的批发价格,但应根据销售商的风险厌恶情况制定不同的回购价格,销售商越厌恶风险,设定的回购价格就越高;第二、在有效回购契约中,销售商成本分担比例越大,批发价格和回购价格应设置得越低,且回购价格下调的速度更快;第三、单边转移支付具有一定的渠道协调功能,供应商可在需求信息不对称下借助这一机制来协调供应链. 本文是在假定供应商知晓销售商风险厌恶信息的基础上进行的研究,放松这一假设是未来的研究方向之一.另一个研究方向是考虑供应商也风险厌恶的情形. [1]肖玉明,汪贤裕.边际成本递增情况下供应链的协调研究[J].系统工程学报,2009,24(1):94–98. Xiao Yuming,Wang Xianyu.Research on coordination of supply chain with increasing marginal costs[J].Journal of Systems Engineering,2009,24(1):94–98.(in Chinese) [2]申成霖,张新鑫,卿志琼.服务水平约束下基于顾客策略性退货的供应链契约协调研究[J].中国管理科学,2010,18(4):56–64. Shen Chenglin,Zhang Xinxin,Qing Zhiqiong.Supply chain contracts coordination with consumer’s strategic returns policies under the service level constraint[J].Chinese Journal of Management Science,2010,18(4):56–64.(in Chinese) [3]刘家国,吴 冲.基于报童模型的两级供应链回购契约协调研究[J].中国管理科学,2010,18(4):73–78. Liu Jiaguo,Wu Chong.Study of a tow-level supply chain returns policy model based on the newsboy model[J].Chinese Journal of Management Science,2010,18(4):73–78.(in Chinese) [4]Su X.Consumer returns policies and supply chain performance[J].Manufacturing&Service Operations Management,2009,11(4): 595–612. [5]孙彩虹,于 辉.如何恰当激励零售商的过程创新行为[J].系统工程学报,2008,23(6):702–707. Sun Caihong,Yu Hui.How to stimulate the retailer’s process innovation decision properly[J].Journal of Systems Engineering,2008,23(6):702–707.(in Chinese) [6]杜少甫,杜 婵,梁 樑,等.考虑公平关切的供应链契约与协调[J].管理科学学报,2010,13(11):41–48. Du Shaofu,Du Chan,Liang Liang,et al.Supply chain coordination considering fairness concerns[J].Journal of Management Sciences in China,2010,13(11):41–48.(in Chinese) [7]代建生,孟卫东.基于RPM的供应链合作促销的协调问题[J].系统工程学报,2014,29(2):223–232. Dai Jiansheng,Meng Weidong.Coordination of supply chain collaborative promotion based on RPM[J].Journal of Systems Engineering,2014,29(2):223–232.(in Chinese) [8]Krishnan H,Kapuscinski R,Butz D A.Coordinating contracts for decentralized supply chains with retailer promotional effort[R].Working Paper,Ann Arbor:University of Michigan,2003. [9]Taylor T A.Supply chain coordination under channel rebates with sales effort effects[J].Management Science,2002,48(8):992–1007. [10]Krishnan H,Kapuscinski R,Butz D A.Coordinating contracts for decentralized supply chains with retailer promotional effort[J].Management Science,2004,50(1):48–63. [11]徐 最,朱道立,朱文贵.销售努力水平影响需求情况下的供应链回购契约[J].系统工程理论与实践,2008,28(4):1–11. Xu Zui,Zhu Daoli,Zhu Wengui.Supply chain coordination under buy-back contract with sales effort effects[J].Systems Engineering:Theory&Practice,2008,28(4):1–11.(in Chinese) [12]姚泽有.考虑努力及退货价格因素的易逝品供应链退货政策模型[J].预测,2010,29(6):48–51+56. Yao Zeyou.Return policy model with effect and return price in perishable product’s supply chain[J].Forecasting,2010,29(6):48–51+56.(in Chinese) [13]Schweitzer M E,Cachon G P.Decision bias in the newsvendor problem with a known demand distribution:Experimental evidence[J].Management Science,2000,46(3):404–420. [14]Dai J,Meng W.A risk-averse newsvendor model under marketing-dependency and price-dependency[J].International Journal of Production Economics,2015,160:220–229. [15]Chen F Y,Xu M,Zhang,Z G.A risk-averse newsvendor model under the CVaR decision criterion[J].Operations Research,2009,57(4):1040–1044. [16]Gan X H,Sethi S,Yan H.Supply chain coordination with a risk-averse retailer and a risk-neutral supplier[J].Production and Operations Management,2004,13(2):135–149. [17]Gan X H,Sethi S,Yan H.Channel coordination with a risk-neutral supplier and a downside-risk-averse retailer[J].Production and Operations Management,2005,14(1):80–89. [18]Choi T M,Li D,Yan H.Mean-variance analysis of a single supplier and retailer supply chain under a returns policy[J].European Journal of Operational Research,2008,184(1):356–376. [19]Yang L,Xu M,Yu G.Supply chain coordination with CVaR criterion[J].Asia-Pacifc Journal of Operational Research,2009,26(1):135–160. [20]Gan X,Sethi S P,Yan H.Coordination of supply chains with risk-averse agents[C]//Choi T M,Cheng T C E.ed.,Supply Chain Coordination under Uncertainty.Berlin:Springer-Verlag,2011:3–31. [21]Artzner P,Delbaen F,Eber J M,et al.Coherent measures of risk[J].Mathematical Finance,1999,9(3):203–228. [22]Pfug G C.Some remarks on the value-at-risk and the conditional value-at-risk[C]//Uryasev S.ed.,Probabilistic Constrained Optimization:Methodology and Applications.Dordrecht:Kluwer Academic Publishers,2000:1–11. [23]Rockafellar R T,Uryasev S.Conditional value-at-risk for general loss distributions[J].Journal of Banking and Finance,2002,26(7):1443–1471. 附录 文中定理的证明 引理1的证明 把v的定义域化分为三个区间,由式(8),有 将其置入式(8),有 命题1的证明 由式(9),g(v∗(y,e),y,e)关于y,e是凹函数,其一阶必要条件也是其取得极值的充分条件.对其求关于y和e的一阶偏导,得 命题3的证明 运用隐函数定理,对式(11)两边求关于η的导数,得到 第二部分的证明.由式(21),有CVaRη((ϕ))>0,∀ϕ;由式(19),又有E(0)=EC>0,因而一定存在ϕ∈(0,1]使得CVaRη((ϕ))>0和E(ϕ)>0同时成立,而确保了b∗(ϕ) 定理2的证明 第一部分的证明.根据定义4,有效契约必须满足参与约束和激励相容条件.注意到(w∗(ϕ),b∗(ϕ),ϕ)是激励相容的,而由式(20)可知,对任意契约安排(w∗(ϕ),b∗(ϕ),ϕ),恒有CVaRη((ϕ))>0,因而只需考虑供应商的参与约束.由式(20),有(1−ϕ)>ϕ(1−η)pE[yI∗−eI∗ξ,0]+,将式(18)代入上式,简单变形,可得式(22). 第二部分的证明.当供应商不清楚市场需求分布时,其设计的契约要适用于所有分布.将式(22)简单变形得 下证,只要ϕ>0,总存在某一需求分布函数,使上述条件不能成立. Buy-back contracts of a supply chain with a risk-averse retailer exerting sales effort Dai Jiansheng,Meng Weidong This paper investigated channel coordination via buy-back contracts for a supply chain with a riskaverse retailer exerting sales effort based on CVaR criterion.It discussed the retailer’s ordering and sales effort decision and explored how the retailer’s sales effort and risk aversion affect his optimal ordering quantity.It investigated two kinds of buy-back and cost-sharing contract,respectively,with unilateral transfer pay and without unilateral transfer pay.Neither of the two contracts can coordinate the supply chain,if the retailer is extremely risk averse,i.e.,the risk averse coeffcient of the retailer is smaller than the critical value.Otherwise, both of them can achieve channel coordination in the case of symmetric information on demand distribution. However,only the former can coordinate the supply chain under informational asymmetry.Finally,it examines the feasible region and parameters relationships of the optimal contracts,as well as the channel proft allocation by means of a numerical analysis. supply chain;buy-back contract;sales effort;risk aversion C94;F274 A 1000−5781(2015)04−0519−11 10.13383/j.cnki.jse.2015.04.009 2012−05−21; 2012−11−19. 国家自然科学基金资助项目(71462023;71461014;71162019);昆明理工大学管理与经济学院热点(前沿)领域科研支撑计划资助项目(QY2015046). 代建生(1978—),男,四川华蓥人,博士,研究方向:供应链协调等,E-mail:jiansheng.dai@163.com; 孟卫东(1964—),男,重庆人,教授,博士生导师,研究方向:战略管理、机制设计等,E-mail:mengweidong@cqu.edu.cn.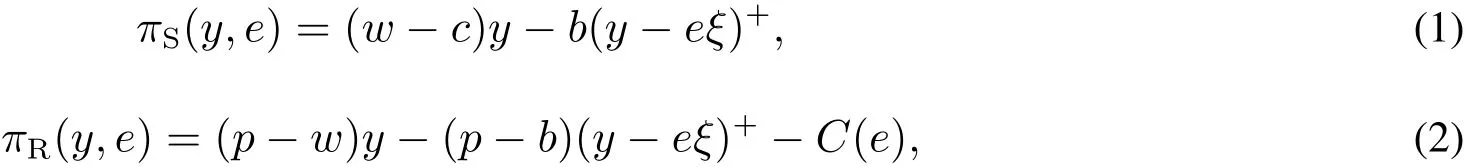
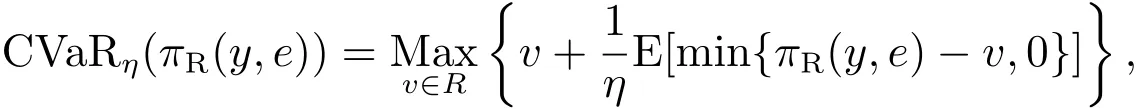
3 订购和促销决策分析

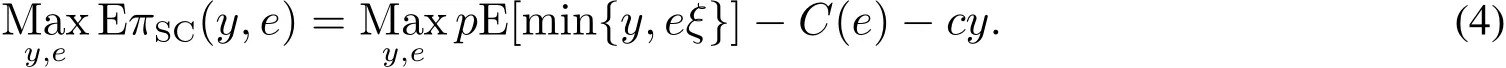
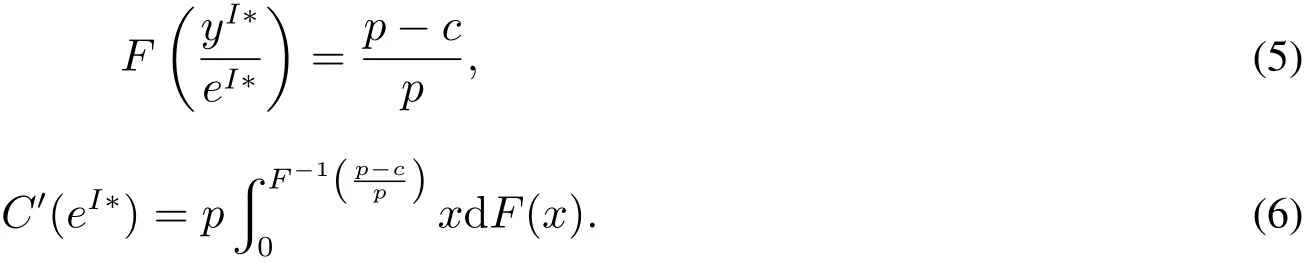

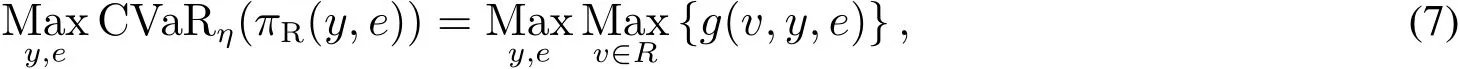


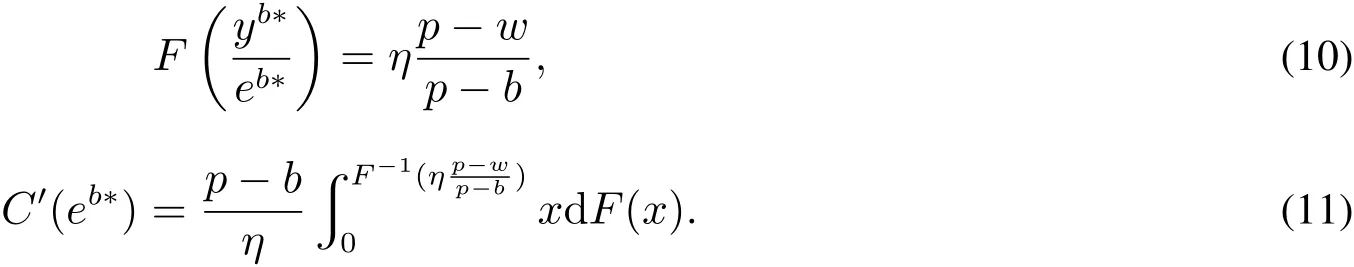
4 回购契约的协调

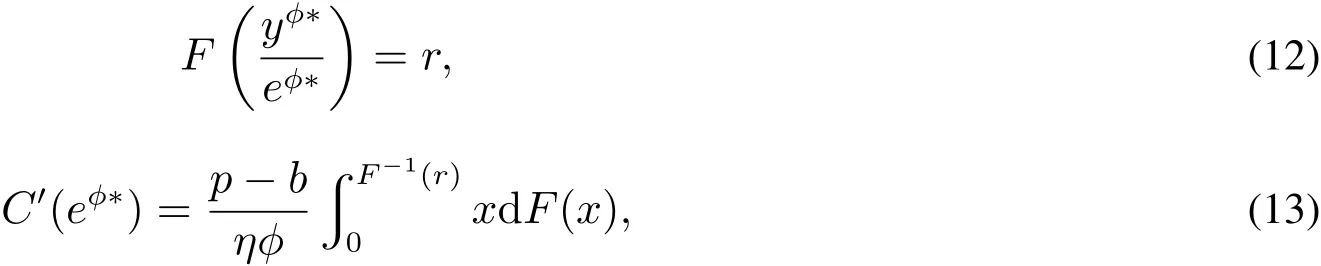
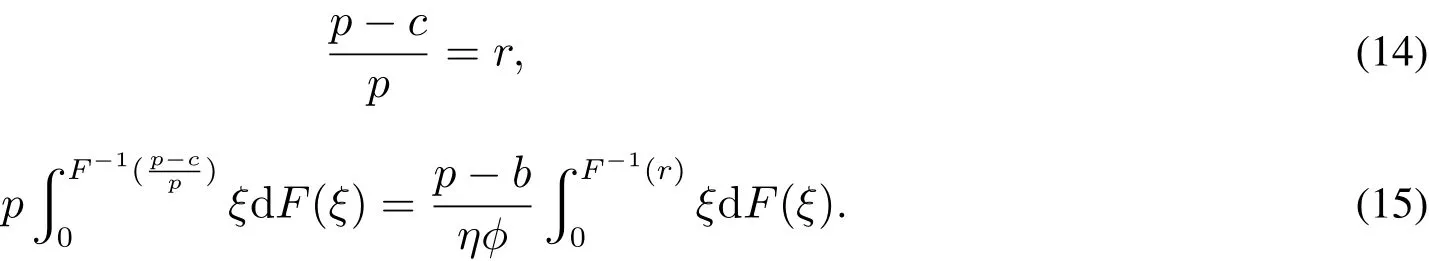


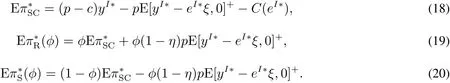

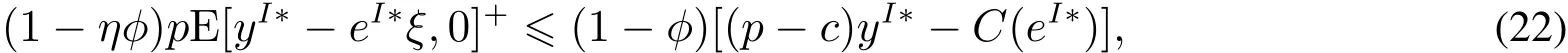
5 数值分析


6 结束语
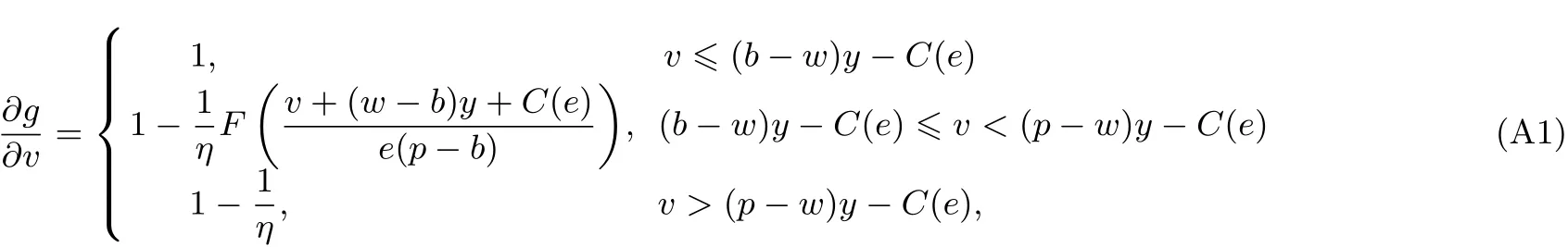
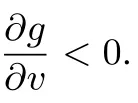
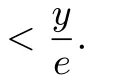

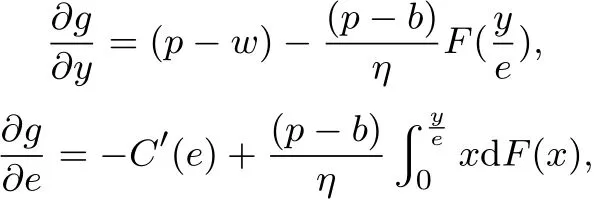


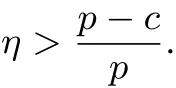

(College of Economics and Business Administration,Chongqing University,Chongqing 400030,China)
