多目标中间包计划模型及混合优化算法
2015-10-26马天牧罗小川柴天佑
马天牧,罗小川∗,柴天佑,2
(1.东北大学流程工业综合自动化国家重点实验室,辽宁沈阳110819; 2.东北大学自动化研究中心,辽宁沈阳110819)
多目标中间包计划模型及混合优化算法
马天牧1,罗小川1∗,柴天佑1,2
(1.东北大学流程工业综合自动化国家重点实验室,辽宁沈阳110819; 2.东北大学自动化研究中心,辽宁沈阳110819)
中间包计划是重要的炼钢–连铸批量计划之一,其功能是在给定的炉次计划中,根据炼钢–连铸生产能力及下游工序生产所需材料的数量,挑选出待生产的炉次并制定出合理的中间包使用数量及每个中间包内生产的炉次.在对中间包计划问题描述的基础上及现有文献中未考虑中间包利用率及中间包内炉次宽度差异性,建立了多目标中间包计划数学模型.为了求解模型将模型分解为两个子模型,并针对两个子模型设计了迭代局部搜索算法(iterated local search,ILS)及变邻域搜索算法(variable neighborhood search,VNS)相结合的双层混合算法,考虑到中间包利用率及多目标权重对解的影响,在算法中加入了可调整模型参数的方法,最后用实际生产数据对模型及算法进行验证.
中间包计划;多目标;迭代局部搜索;变邻域搜索;混合算法
1 引 言
炼钢–连铸工序是整个钢铁生产过程的瓶颈工序,其特点是生产前设备准备时间长,生产过程中要求高温连续,生产的产品必须能够充分供应后续工序生产需求.因此合理有效制定其生产计划可以充分提高设备利用率、减少设备因停机准备的时间,使前后工序协调生产.炼钢–连铸生产计划的管理分为批量计划和调度计划,其中批量计划的功能是确定每日或班组的生产任务,包括炉次计划、中间包计划、浇注计划,调度计划的功能是为生产任务确定设备及生产起止时间.本文主要讨论中间包计划.中间包计划是在炉次计划的基础上,负责考虑在满足本工序生产能力的同时,还要满足其下游生产工序正常生产所需原料的供给,其作用重于炉次计划.炼钢–连铸生产过程涉及的设备种类多、工艺路径复杂,其调度计划一直是国内外学者和工程技术人员研究的热点,对调度计划的研究从静态调度发展到动态调度、重调度和钢包调度[1−5].而对批量计划研究较少[6],目前对中间包计划研究较为深入的有文献[7,8].文献[7]提出了中间包批量计划,并将其归结为车辆路径问题(vehicle routing problem,VRP),以最少中间包数、未组入中间包炉次惩罚、下游工序需求为目标.文献[8]将中间包计划归结为能力受限的调度问题建立了多目标模型,其在目标中考虑了最少中间包数、下游工序需求,开发了新型的变邻域搜索方法.但两者没有考虑中间包利用率变化及炉次宽度区间相似性,且都仅采用一组实例数据验证.在工厂里中间包计划主要是由计划人员采用试凑的方法编制,计划的质量取决于人的经验,并且每次都需耗费大量的时间.
基于以上问题,本文以某大型钢铁企业实施制造执行系统(manufacturing execution system,MES)项目为背景,在描述该企业的中间包计划问题基础上,建立多目标的中间包批量计划数学模型.为了求解模型,首先将模型分解为两个子模型,然后设计了迭代局部搜索与变邻域搜索相结合的双层混合优化算法,由于中间包利用率是可变化的且对问题的解有影响,同时考虑到多目标转换为单目标时权重对解也有影响,因此在算法中加入了动态改变中间包利用率及权重的方法,最后采用现场中多组数据进行验证.
2 中间包计划问题描述及数学模型
2.1 问题描述
在炼钢–连铸生产中,中间包是连铸机上用来盛钢水的容器.中间包具有一定的使用寿命,根据所盛钢水的成本不同使用寿命不同,一般在4炉~6炉,且不论是否达到使用寿命都需要对其耐高温层维护,每次维护的成本是很可观的[7].使用同一中间包浇铸的钢水成份和相应板坯浇铸宽度必须相同或相近.当出现钢水成份或宽度调整(宽度每次调整幅度最大100 mm,最小50 mm)时,会分别出现叫做交接坯和梯形坯的两类板坯.这两类板坯在实际生产中都是需要减少或避免的。
在制定中间包计划时,其输入是炉次计划和生产指标,炉次计划给定了炉次的数量及每个炉次的属性,这些属性包括出钢记号,炉次所生产板坯的最大宽度、最小宽度,炉次是否为精炼炉,可用于下游工序使用的板坯重量(可能包含一个工序或几个工序的加工量)、所需要中间包的类型.生产指标中给定了下一个生产周期所要生产的总炉次数目标及上、下限,总精炼炉次数目标及上、下限,热轧工序所需要的烫辊材目标重量及上大下限,热轧工序下游各机组所需要加工板坯的目标重量及上、下限.中间包计划的任务就是满足生产约束的前提下使用最少的中间包数量在给定的炉次计划中挑选炉次以达到生产指标中给定的目标或范围.
2.2 数学模型
下面介绍本文使用的数学符号:炉次集合N={1,2,...,n},中间包集合M={1,2,...,m},下游生产工序集合F={1,2,...,f},i,j为炉次号,i∈N,j∈N.k为中间包号,k∈M.l为生产工序号,l∈F.炉次相关属性如下:炉次的宽度区间为Ii=[w,w],炉次的出钢记号为sgi,炉次未组入中间包的惩罚成本为bi,炉次宽度所对应的数值为vi,炉次i中所包含烫辊材的重量为hi,炉次i的精炼标志为ri,炉次i所使用的中间包类型号为tsgi,炉次i包含下游生产工序l所需要板坯重量为fil.中间包相关属性如下:中间包k的使用寿命为Tk,中间包k的使用成本为sk,中间包寿命使用系数为β.生产约束相关符号:宽度调整的最大幅度为△whMax,宽度调整次数为△n.生产指标相关符号:生产指标中规定的目标炉次数、上限、下限为CHG、CHU、CHL,生产指标中规定的可生产的精炼炉次数目标、上限、下限为RHG、RHU、RHL,生产指标中规定的热轧工序所需要的烫辊材(用来加热热轧轧辊的板坯)目标重量、上限、下限为HG、HU、HL,生产指标中规定的下游工序l所能生产的目标重量、上限、下限为、、.其它参数:炉次i与炉次j组入到同一中间包的惩罚系数为cij,根据以下三个式子计算得到,即

其中r1、r2、r3为常数,D为比较大的常数,式(3)中的vi是由炉次的宽度区间计算得到的,可以通过该数值来计算宽度区间的差异,vi的计算过程采用文献[9]计算区间数排序向量的步骤:
步骤1基于S函数的相对优势度公式(4)对区间数进行两两比较,将P(Ii≻Ij)简写为pij,则所建立的相对优势度矩阵为P=(pij)n×n.
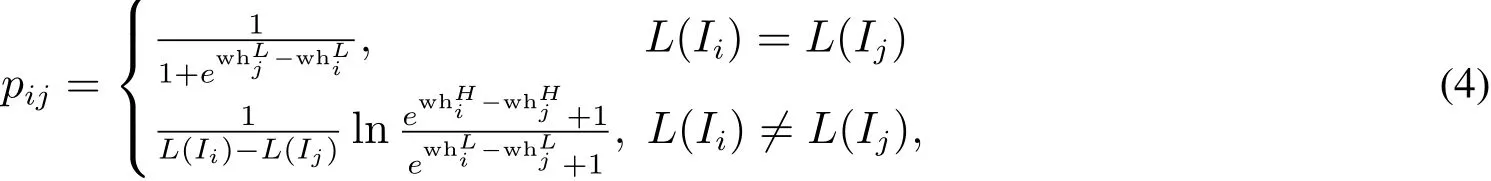
引入如下决策变量


中间包计划的数学模型为


其中目标函数式(5)第一项表示中间包使用成本,第二项表未组入中间包炉次惩罚成本,第三项表示中间包剩余使用寿命,第四项表示组入到同一中间包内炉次间差异.目标函数式(6)表示最小化组入中间包计划的炉次数与生产指标规定的目标炉次数的差.目标函数式(7)表示最小化组入中间包计划的精炼炉次数与生产指标规定的目标精炼炉次数的差.目标函数式(8)表示最小化组入中间包的烫辊材重量与生产指标规定的目标烫辊材重量的差.目标函数式(9)表示最小化组入中间包的各下游机所需加工板坯重量与生产指标规定的各下游机组所需加工板坯目标重量的差.约束式(10)确保炉次最多只能组入到一个中间包内.约束式(11)确保组入到中间包内的炉次必须满足中间包的使用寿命.约束式(12)~(15)是生产指标约束.约束式(16)、(17)分别为宽度调整幅度、次数约束.约束式(18)确保组入到同一梓里包内的炉次的中间包类型必须相同.式(19)、(20)是变量定义.
中间包计划模型实质是经典装箱的扩展.忽略目标式(6)~(9),及目标函数式(5)中的第二、三、四项时,及约束式(12)~(18)时,模型就成为变成本的装箱问题;在此基础上加入式(5)中的第二项,则模型是带有拒绝成本的装箱问题.而这两种装箱问题的求解在文献中都被证明是NP-hard,于是经典装箱问题是中间包计划模型的一个特例,且输入的炉次数一般在100炉~300炉之间,因此在实际应用中需要开发有效的启发式算法以快速求解.
3 可动态调整参数的双层ILSVND混合算法
3.1 模型分解
观察模型,可以看到式(5)含义是用最少的中间包生产给定的炉次,若将中间包看作箱、炉次看作物品,那么该问题可以归结为装箱问题;而式(6)~(9)及约束(12)~(15)是规定组入中间包的炉次必达到的目标和约束.约束(12)~(15)描述的是下游工序机组的能力,结合目标(6)~(9),将该子问题看作是背包问题.这样看来,中间包计划问题包含了装箱和背包两种问题在里面.由此可以想到两种策略达到上述目的.第一种策略是先考虑背包再装箱,即首先根据约束(12)~(15)先选择炉次,然后将炉次组成中间包,最后以炉次为单位进行局部优化.第二种策略是先考虑装箱主考虑背包,即先将炉次组成中间包,然后根据约束选择中间包,最后分别以中间包和炉次为单位进行局部优化.但第一种策略存在的问题是,由于缺少对“箱子”的约束而难以保证根据能力约束选择出的炉次所组成的中间包数的数量是最少的.因此选择第二种策略.根据第二种策略,将模型分解为两个模型,第一个模型的目的是将炉次组成中间包,将其叫做组中间包模型,用M1表示该模型;第二个模型的目的是选择中间包和炉次,将其叫做选中间包模型,用M2表示该模型.则这两个模型可以表示如下
M1:

M2:
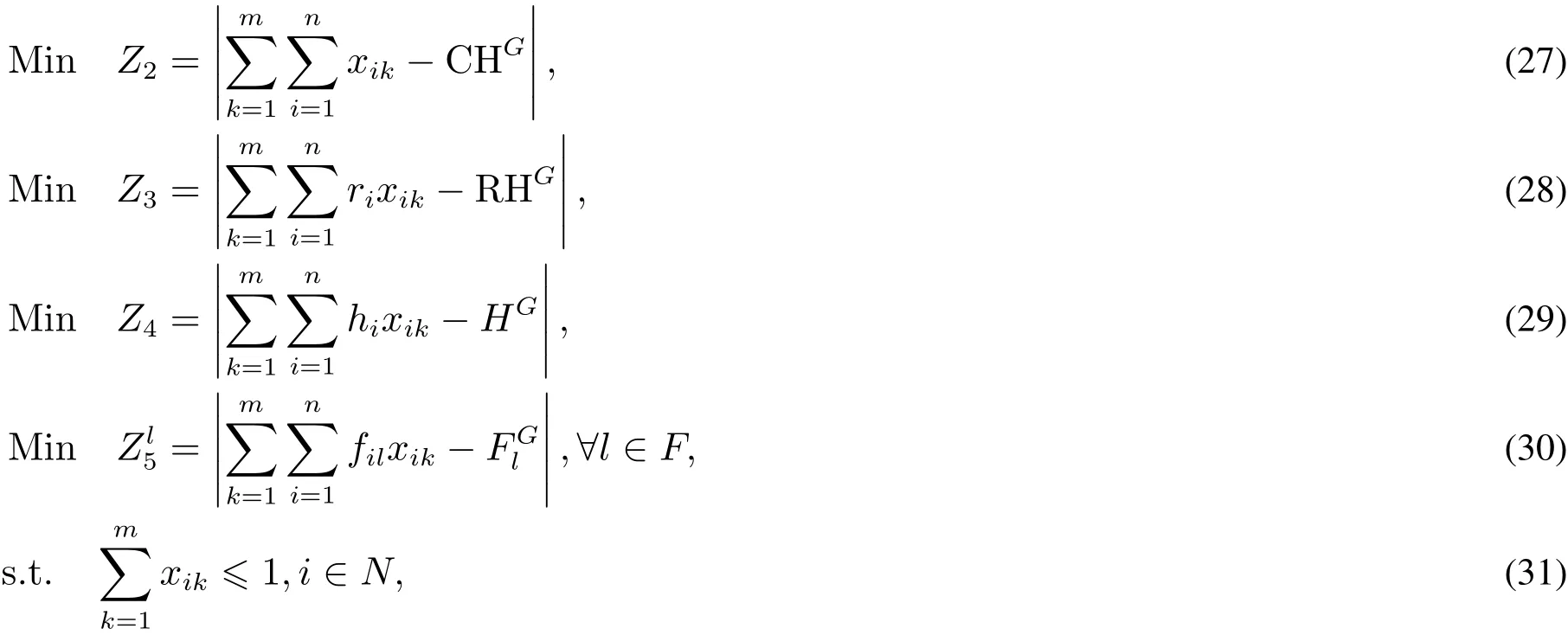



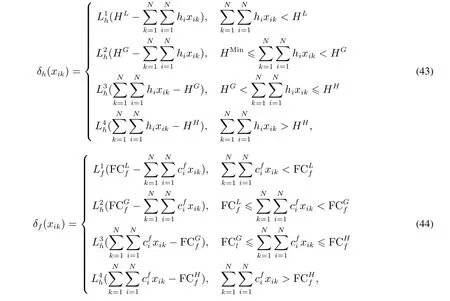
3.2 ILSVND混合优化算法
本文采用ILS与VND算法相结合的混合算法对中间包计划模型求解.ILS和VNS两种启发式算法提供了简洁而有力的局部搜索能力.两种算法在组合优化、调度[10]、车辆路径[11]、选址[12]等实际问题中得到了应用.ILS算法首先构造初始解,然后采用迭代机制通过内部的局部搜索方法(local search)和摄动方法(perturbation)构建一系列解,最后通过某些准则输出历史最好解.其中最重要的两个步骤是局部搜索和摄动,摄动步骤就是用来做局部搜索无法做到的一些对解的改动.VND(variable neighborhood descent)是VNS算法的一个扩展.该算法起始于一个初始解和邻域结构集合.在每步迭代中,算法寻找每个邻域结构中最小目标函数值的解,并与原来的解比较以选择邻域结构.最后输出最好的解[13,14].
前一节,将整个中间包计划模型分解为两个子模型.两个子模型中都含有参数,其中第一个子模型有三种参数:中间包使用成本、中间包剩余容量单位惩罚成本、中间包利用率三个参数,第二个子模型中的参数是加权系数.通常情况下,这些参数都是在算法求解模型之前根据经验确定的,在算法计算过程中这些参数不变.然而对于中间包计划模型,这样做存在两个问题:1)当第一个子模型的参数确定后得到的较好的解,不能够保证第二个子模型得到较好的解.2)第二个子模型的目的是在较充分使用中间包寿命的前提下,所选择的中间包及炉次尽量与生产指标中给定的目标值相近,而固定的权重值不能反映算法求解过程中得到的解与生产指标差异的大小.
为了解决以上两个问题,设计了如图1所示的具有动态调整模型参数的混合算法框架.在图1中,r表示生产指标给定值,y表示算法求解后得到的生产指标值.将两者进行比较得到差值e,利用这个差值及更新目标权重操作修改第二子模型中的权重值λ(包括λch、λrh、λh、λl).更新中间包利用率操作的目的是在算法求解过程中调整第一个子模型中的中间包利用率参数β.下面先介绍算法中的主要步骤:生成初始解、邻域操作、调整权重系数、调整中间包利用率,最后给出整个算法的步骤.
算法1中两个初始解操作都采用启发式算法.第一层ILSVND算法的初始解,首先按炉次的最小宽度降序排序,当炉次最小宽度相同时,按其最大宽度降序排序,对排好序的炉次集合利用求解装箱算法的最佳适应算法(best ft,BF)规则将炉次组成中间包,得到的初始解记为x0.第二层ILSVND算法的初始解采用贪婪算法.具有步骤为,对中间包按中间包内炉次数降序排序,根据约束(13)挑选精炼炉次,满足约束后再根据约束(12)挑选炉次,直到满足约束为,得到的解记为s0.
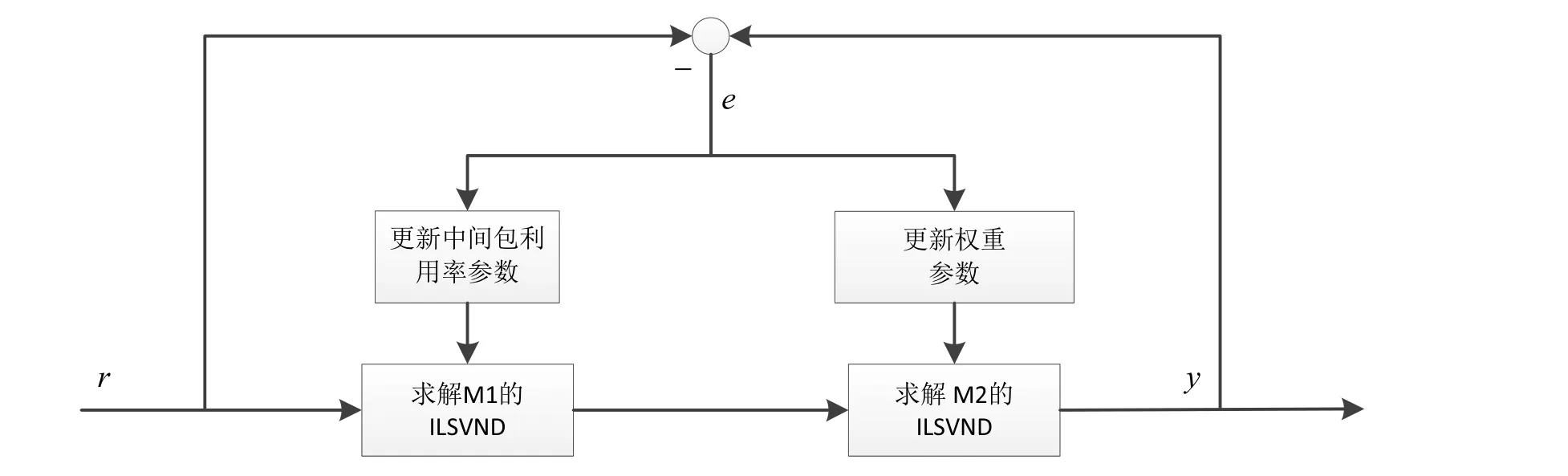
图1 具有参数动态调整的双层ILSVND混合算法框架Fig.1 Algorithm framework of double layers ILSVND with adjusting parameters dynamically
3.2.1 生成初始解
算法1中两个初始解操作都采用启发式算法.第一层ILSVND算法的初始解,首先按炉次的最小宽度降序排序,当炉次最小宽度相同时,按其最大宽度降序排序,对排好序的炉次集合利用求解装箱算法的最佳适应算法(best ft,BF)规则将炉次组成中间包,得到的初始解记为x0.第二层ILSVND算法的初始解采用贪婪算法.具有步骤为,对中间包按中间包内炉次数降序排序,根据约束(13)挑选精炼炉次,满足约束后再根据约束(12)挑选炉次,直到满足约束为,得到的解记为s0.
3.2.2 邻域操作
在使用VND算法中,设计了如下几种邻域操作,其中N1~N4针对第一层ILSVND算法,N5~N8针对第二层ILSVND算法.
N1–交换中间包炉次.在中间包数不变的前提下,该邻域操作通过交换已组入中间包的炉次来试图改善目标函数(5)中同一中间包内炉次间差异.首先在当前解中任意选择两个中间包,并在每个中间包内任意选择一个炉次,如果在满足停止条件前,这种交换能够满足约束并改善目标函数,则接受该交换.
N2–插入炉次.在中间包数不变的前提下,该邻域操作通过将未组入中间包的炉次插入到中间包中来改善目标函数(5)中中间包使用寿命、减少未组中间包的炉次及中间包内炉次间差异.首先在当前解中选择一个中间包及未组中间包的炉次,将该炉次插入到选择的中间包内,若在满足停止条件前该操作能够满足约束及改善目标函数,则将炉次插入到中间包内.
N3–移除炉次.在中间包数不变的前提下,该邻域操作通过移除炉次来改善目标函数(5)中中间包内炉次间差异.首先在当前解中任意选择一个中间包,将该中间包内的炉次分别移除,若在满足停止条件前,该操作能够改善目标函数的话,则接受该操作.
N4–交换中间包炉次与未组中间包炉次.在中间包数不变的前提下,该邻域操作试图将通过交换已组入中间包的炉次与未组入中间包的炉次来改善目标函数(5)中的未组中间包炉次惩罚成本及中间包内炉次间差异.首先在当前解中任意选择一个中间包,将该中间包内的炉次分别与未组中间包的炉次交换,若在满足停止条件前,这种交换能够改善目标函数,则接受该操作.
N5–交换已选中的中间包与未选中的中间包内炉次.在生成第二个子模型的初始解后,整个解包含三部分:选中的中间包、未选中的中间包、未组中间包的炉次.该操作针对目标函数(21),在炉次数不变的前提下,交换选中的中间包与未选中的中间包内炉次.首先任意选择一个已选中的中间包,在任意选择一个未选中的中间包,逐个交换两个中间包的炉次,若在满足停止条件前,这种交换操作能够改善目标函数(21),则接受该交换操作.
N6–交换选中的中间包炉次与未组中间包炉次.该操作针对目标函数(21),在炉次数不变的前提下,将选中的中间的炉次与未组中间包的炉次进行交换,若在满足停止条件前,该操作能够改善目标函数,则接受该操作.
N7–插入炉次.该操作针对目标函数(21),通过将未组中间包的炉次或未选中中间包内炉次插入到选中的中间包内来改善目标函数.在当前解中选择还有剩余容量的中间包,将未组中间包的炉次插入到该中间包内,若在满足停止条件前,这样的插入操作能够改善目标函数,则接受该操作.
N8–移除炉次.与N7相反,该操作针对目标函数(21),通过移除选中的中间包内的炉次来改善目标为数.在当前解中任意选择一个中间包,分别移除该中间包的炉次,若在满足停止条件前,该操作能够改善目标函数,则接受移除操作.
3.2.3 调整权重系数
算法中的更新目标权重操作用来对各目标权重系数进行调整,权重系数的调整如下
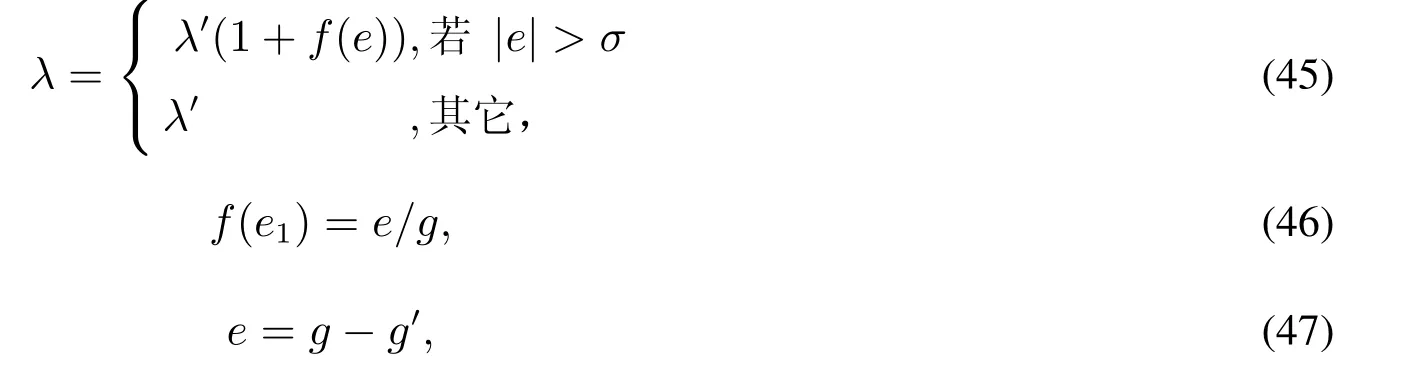
其中λ和λ′分别表示某一目标的权重系数的当前值及前值,σ表示一个给定的正数,e表示当前指标差异值,g表示指标的目标值,g′表示当前算法得到的实际值.
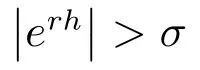

3.2.4 调整中间包利用率
算法中的更新中间包利用率操作用来对子模型M1中的中间包利用率系数进行调整.一般来说中间包成本及剩余容量的成本在一定时期内是固定不变的,即子式(5)中的sk和pk,中间包使用寿命的利用率是可变的.β对模型的影响表现在中间包空间的利用上.例如当β=0.5时,表示当中间包的使用寿命达到一半时就认为对该中间包使用寿命的利用是充分的,这种情况下就增加了中间包的数量.当β=1时,就要求中间包使用寿命必须全部利用上,不允许有剩余使用空间,这种情况下就减少了中间包的数量.而中间包数量的多与少,对子模型M2是有影响的.当中间包数少时,可能选择不出满足指标的炉次数,而当中间包数多的时候,中间包剩余的使用寿命又可能会太多.因此为改善这种情况采用如下策略:在某一固定的β下,通过求解模型M1及M2得到一个解,当该解在调整权重后仍没有改进时,通过式(51)改变β值,β′为当前循环周期内中间包利用率的值,当β′+0.1>1时取β=β′−0.1,当β′−0.1<0.6时,取β=β′+0.1,且规定中间包的利用率必须在一半以上,即β>0.6.

3.2.5 摄动
在第一层VND算法中,所有的邻域操作都是在中间包数目不变的前提下进行的.中间包数变化时,其影响到的炉次是邻域结构所不能描述的,但其对解确实有影响.因此将这种因中间包数变化对解的影响作为摄动操作.中间包数的变化是双向的,既可以增加其数量,又可以减少其数量.把这两个方向的变化都作为第一层算法的摄动操作.对于第二层算法,将随机选择选中的中间包内炉次与未选中中间内炉次及未组中间包炉次交换作为摄动操作.
下面给出整个算法的步骤,其中步骤1~步骤6是第一层ILSVND混合算法,步骤7~步骤14是第二层ILSVND混合算法.对于新解接受标准,本算法中采用接受较好解的方法,非支配排序负责对多个解进行非支配排序.
步骤1生成初始解x0;
步骤2对x0进行变邻域搜索得到x∗; /*即用变邻搜索搜索算法替换原算法中的局部搜索*/
步骤3对x∗进行摄动操作得到解x’;
步骤4对解x’进行变邻域操作得到解x∗’; /*即用变邻搜索搜索算法替换原算法中的局部搜索*/
步骤5根据接受标准对x∗、x∗’进行是否接受的判断并得到解x∗;
步骤6若未达到循环迭代次数最大值,则转步骤7,否则转步骤3;
步骤7根据x∗生产初始解s0;
步骤8对解s0进行变邻域搜索得到解s∗; /*即用变邻搜索搜索算法替换原算法中的局部搜索*/
步骤9对解s∗进行摄动操作得到解s’;
步骤10对解s’进行变邻域操作得到解s∗’; /*即用变邻搜索搜索算法替换原算法中的局部搜索*/
步骤11根据接受标准对解s∗,s∗’进行是否接受的判断并得到解s∗;
步骤12若达到循环迭代次数最大值,则转步骤13,否则转步骤9;
步骤13更新权重参数,转步骤9,否则转步骤;
步骤14若达到循环迭代次数最大值,转步骤15,否则转步骤9;
步骤15更新中间包利用率参数;
步骤16若未到循环迭代次数最大值,更新权重参数,转步骤17,否则转步骤7;
步骤17若未达到循环迭代次数最大值,更新权重参数,转步骤1,否则转步骤18;
步骤18对解进行非支配排序;
步骤19输出解s∗.
4 算例验证

表2中给出了ILSVND算法、标准ILS算法及人工编制的结果对比,其中β是模型中的中间包利用率系数,“定权重”表示固定多目标权重方法,“变权重”表示本文所提出的变化目标权重方法.从表中可以看出:1)各个实例出现的最好解所对应的β值是不同的,例如实例1在β=1,0.8,0.6出现比较好的解,这说明如果像常规求解模型时固定模型参数所得到的结果没有变化参数时的结果好.2)在相同β值下,变目标权重方法得到的结果大部分好于固定目标权重的方法,且变权重方法得到的解与目标值更加接近.3)同一组数据实例, ILSVND算法可以找到几个较好的解供计划员挑选.4)ILS算法同ILSVND算法对比,可以看出无论是变权重还是固定权下,ILS算法得到的结果都没有ILSVND算法好.例如实例2中当β=0.6时,ILS算法得到的总炉次数结果超出生产指标上限5炉,此外该算法得到的大多数结果中都无法均衡的满足生产指标中对烫辊材、各流向的要求.5)与人工计划结果对比,人工计划编制的中间包数普遍比模型得出的结果要多,中间包剩余寿命却比模型得到的结果多,在生产中使用中间包的个数越少说明生产成本越少,中间包剩余使用寿命越少说明中间包利用率越高.
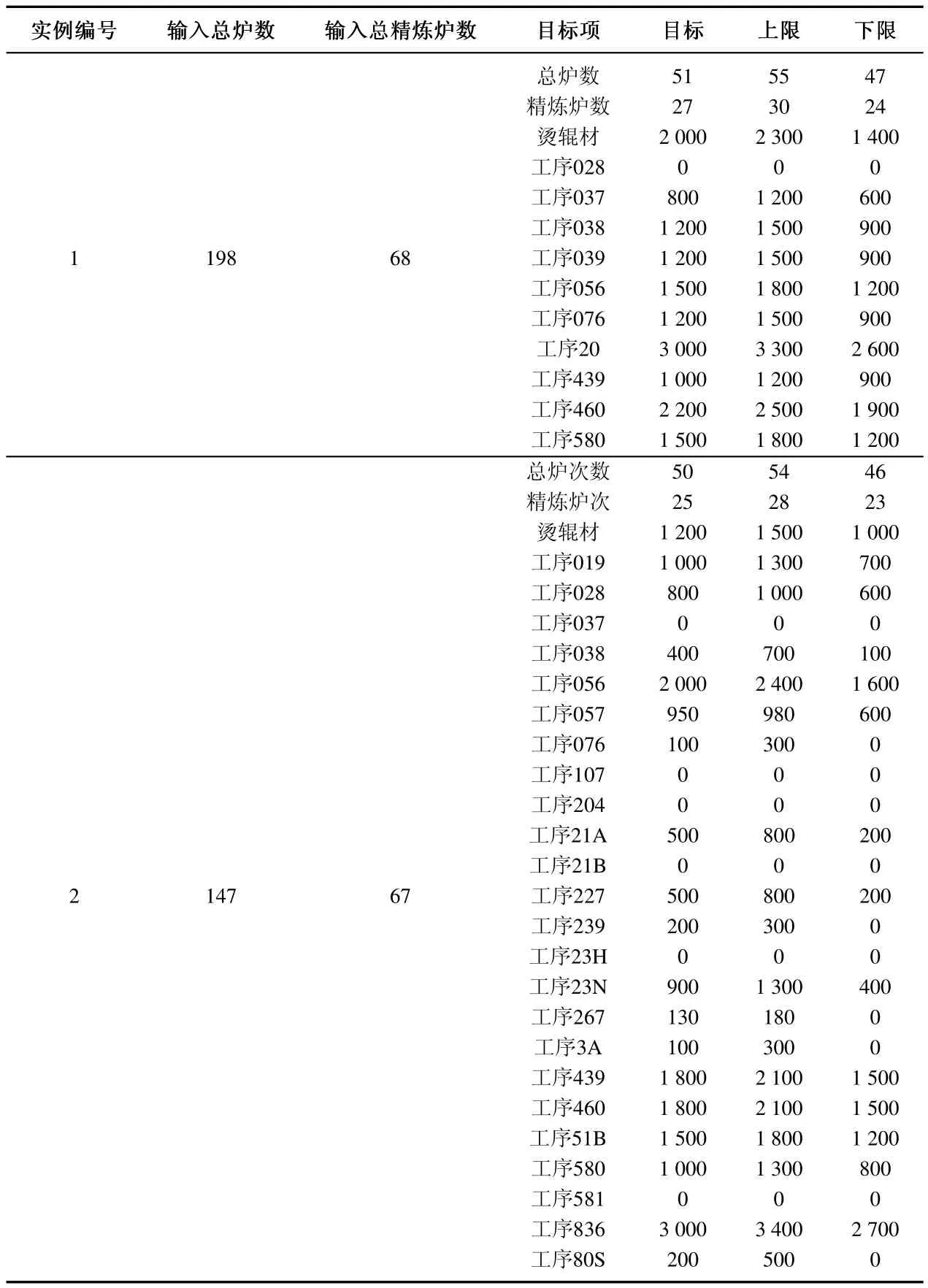
表1 实例数据信息Table 1 Information of problem instances
观察实例2得到的结果,没有完全符合企业给定的目标,例工序037、057等给定的目标值是0,而实际结果却不是0.为此作者对输入的炉次数据进行了分析,发现实例3所对应的炉次中,工序037所需要材料与工序038所需要材料大多数是在同一炉次中,而企业对工序038的目标是生产400 t,这说明要想满足工序038所需要的量,那么必然会有工序037的量在结果中.相同的情况也出现在工序204、工序21B中,这两个工序加工的材料与工序23N均出现在同一炉次中.由此可以看出,炉次计划编制时若考虑将同一工序所需要的材料放在同一炉次中有利于中间包计划的制定.

表2 实验结果Table 2 Experimental result
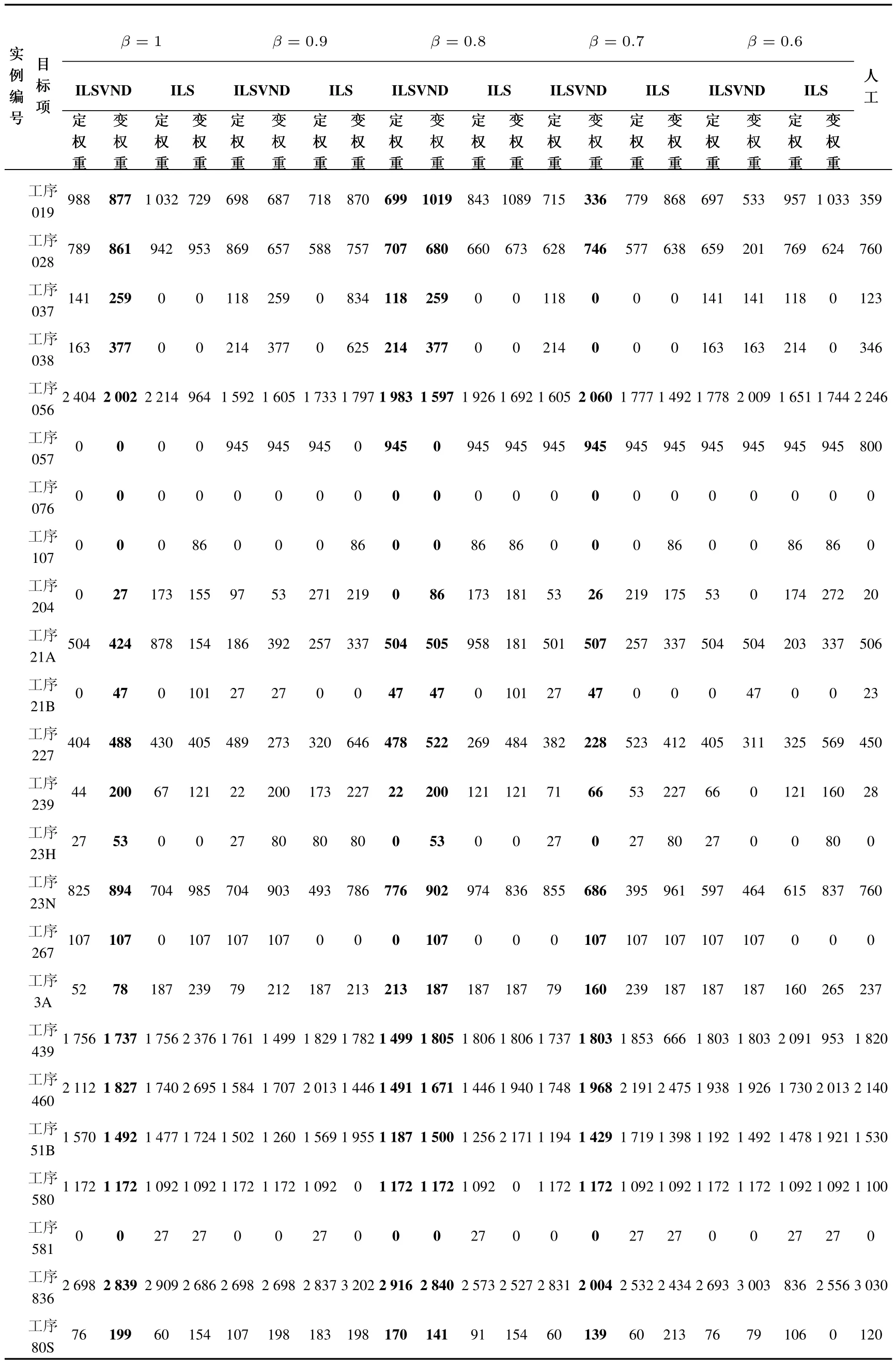
续表2Table 2 Continue
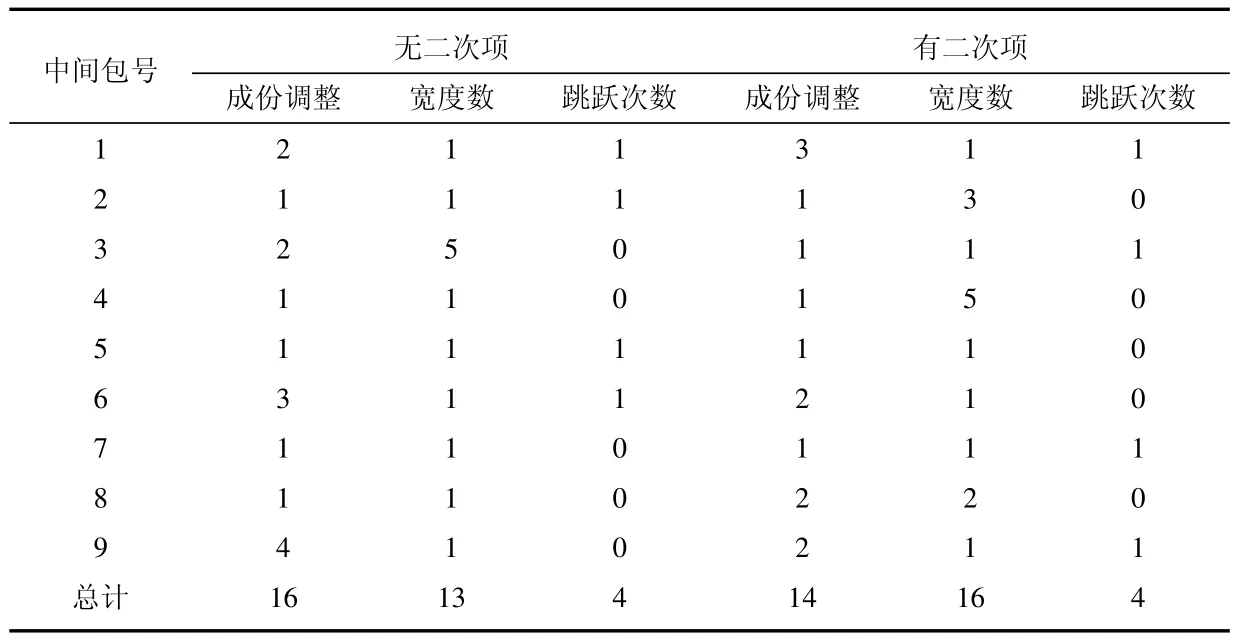
表3 中间包内炉次差异结果对比Table 3 The results of comparing the differences between the charges in tundish
由于模型中的二次项是用来优化中间包内炉次间差异的,因此在表3中给出了实例1中对模型中有二次项及去掉二次项的结果对比.表中成份调整指中间包内炉次出钢记号个数,宽度数表示中间包内炉次可取的宽度数,跳跃次数表示中间包是否进行了宽度调整.从结果中看出,有二次项时中间包内的成份调整次数比模型中无二次项时少2次,而宽度选择的个数多了3个.这说明考虑炉次间差异可以降低中间包内成份的调整次数和增加宽度选择个数,这些都是有利于连铸机连续生产的.
5 结束语
本文针对实际工程中遇到的中间包计划问题,建立了多目标数据模型,第一个目标中综合考虑中间包数、未组入中间包炉次惩罚、中间包利用率及中间包炉次间关系,其它目标则考虑生产能力及炼钢–连铸下游生产需求量.为了求解模型将问题分解为两个子模型,考虑到中间包利用率及多目标权重对解都有影响,在设计迭代局部搜索算法与变邻域搜索算法结合的混合算法中加入了变参数调整功能,最后采用现场实际数据对模型和算法的有效性进行了验证.在实际的验证中发现了炉次计划由于未将具有相同生产方向的材料放入一个炉次中而对中间包计划产生影响,因此下一步需要深入研究这两个计划之间的协调,同时也要研究中间包计划对浇铸计划是否有影响.
[1]Li J,Xiao X,Tang Q,et al.Production scheduling of a large-scale steelmaking continuous casting process via unit-specifc eventbased continuous-time models:Short-term and medium-term scheduling[J].Industrial&Engineering Chemistry Research,2012, 51(21):7300–7319.
[2]庞新富,俞胜平,张志宇,等.炼钢–连铸生产优化重调度方法[J].系统工程学报,2010,25(1):98–103.
Pang Xinfu,Yu Shengping,Zhang Zhiyu,et al.Optima rescheduling for steelmaking-continuous casting[J].Journal of Systems Engineering,2010,25(1):98–103.(in Chinese)
[3]俞胜平,柴天佑,郑秉霖.炼钢连铸混合智能优化调度方法及应用[J].系统工程学报,2010,25(3):379–386.
Yu Shengping,Chai Tianyou,Zheng Binglin.Hybrid intelligent optimal scheduling method for steelmaking and continuous casting and its application[J].Journal of Systems Engineering,2010,25(3):379–386.(in Chinese)
[4]王秀英,柴天佑,郑秉霖.炼钢–连铸调度模型参数优化设定方法[J].系统工程学报,2011,26(04):531–537.
Wang Xiuying,Chai Tianyou,Zheng Binglin.Parameter optimization setting and continuous casting scheduling model[J].Journal of Systems Engineering,2011,26(4):531–537.(in Chinese)
[5]谭圆圆,魏 震,王 森,等.基于VRPTW-AT模型的钢包优化调度方法[J].系统工程学报,2013,28(1):94–100.
Tan Yuanyuan,Wei Zhen,Wang Sen,et al.Optimization algorithm for ladle scheduling based on the VRPTW-AT model[J].Journal of Systems Engineering,2013,28(1):94–100.(in Chinese)
[6]马天牧,罗小川,柴天佑.基考虑转炉容量和宽度的炉次计划混合优化方法[J].系统工程学报,2013,28(5):694–701.
Ma Tianmu,Luo Xiaochuan,Chai Tianyou.Hybrid optimization for charge planning considering the leftover of charge and width[J]. Journal of Systems Engineering,2013,28(5):694–701.(in Chinese)
[7]Tang L X,Wang G S.Decision support system for the batching problems of steelmaking and continuous-casting production[J]. Omega:International Journal of Management Science,2008,36(6):976–991.
[8]Dong H Y,Huang M,Wang X W.Improved variable neighbourhood search for integrated tundish planning in primary steelmaking processes[J].International Journal of Production Research,2012,50(20):5747–5761.
[9]谢 海.基于改进的相对优势度的区间数排序[J].科学技术与工程,2007,8(22):5983–5987.
Xie Hai.Improved relative superiority method for ranking interval numbers[J].Science Technology and Engineering,2007, 8(22):5983–5987.(in Chinese)
[10]Della C,Garaix T,Grosso A.Iterated local search and very large neighborhoods for the parallel-machines total tardiness problem[J]. Computers&Operations Research,2012,39(6):1213–1217.
[11]Laurent B,Hao J K.Iterated local search for the multiple depot vehicle scheduling problem[J].Computers&Industrial Engineering, 2009,57(1):277–286.
[12]Lamb J D.Variable neighbourhood structures for cycle location problems[J].European Journal of Operational Research,2012, 223(1):15–26.
[13]Jarboui B,Derbel H,HanafS,et al.Variable neighborhood search for location routing[J].Computers&Operations Research,2013, 40(1):47–57.
[14]Xiao Y,Kaku I,Zhao Q.A variable neighborhood search based approach for uncapacitated multilevel lot-sizing problems[J].Computers&Industrial Engineering,2011,60(2):218–227.
Multi-objective tundish planning model and hybrid optimization algorithm
Ma Tianmu1,Luo Xiaochuan1∗,Chai Tianyou1,2
(1.State Key Laboratory of Synthetical Automation for Process Industries,Northeastern University,Shenyang 110819, China; 2.Research Center of Automation,Northeastern University,Shenyang 110819,China)
Tundishplanningisoneofthemostfundamentalbatchplanningproblemsinsteelmakingcontinuous casting.It determines how many tundishes are used to produce charges regarding the capacity of steelmaking and the quantity required by the downstream.Based on the description of the tundish planning problem and the shortcoming of existing tundish planning methods in the literature,a multi-objective mathematical model is built.The model was divided into two sub-models for solving,and a two-layer hybrid algorithm is presented by combining the iterated local search with variable neighborhood search.Considering the utilization of tundishes and the weights of multiple objectives,two methods for adjusting the parameters of the algorithm were introduced.Finally,real-world data are used to test the model and algorithm.The results show the effectiveness of the model and algorithm.
tundish planning;multi-objective;iterated local search;variable neighborhood search;hybrid algorithm
*通讯作者
TP273
A
1000−5781(2015)04−0451−15
10.13383/j.cnki.jse.2015.04.003
2013−04−08;
2014−04−03.
国家自然科学基金资助项目(71021061;60974091;61174187;61104174);国家973重点基金研究发展计划资助项目(2009CB320601);高校学科创新引智计划资助项目(B08015).
马天牧(1977—),辽宁阜新人,男,博士生,研究方向:流程工业计划调度,优化算法,Email:mtm309@163.com;
罗小川(1974—),四川西充人,男,博士,教授,博士生导师,研究方向:复杂工业过程运行优化与控制,Email:luoxch@mail.neu.edu.cn;
柴天佑(1947—),甘肃兰州人,男,博士,教授,中国工程院院士,研究方向:流程工业综合自动化,Email:tych@mail.neu.edu.cn.
