双渠道供应链中信息共享价值研究
2015-10-26李庆华
李 波,孙 鹏,李庆华
(天津大学管理与经济学部,天津300072)
双渠道供应链中信息共享价值研究
李 波,孙 鹏,李庆华
(天津大学管理与经济学部,天津300072)
研究了拥有直销渠道的供应链环境中信息共享对各成员定价与利润绩效影响的问题.考虑开设直销渠道的制造商和允许对产品附加增值服务的零售商组成的简单二级供应链,制造商和零售商各自持有部分市场预测信息,零售商还持有产品服务增值成本的私有信息.利用Stackelberg主从博弈模型建模,分析了市场预测信息和增值服务成本信息同时共享或不共享时对制造商和零售商定价和利润的影响.研究发现,信息共享总能使制造商获益,并给出了零售商自愿共享两种私有信息的条件.
供应链管理;双渠道;信息价值;Stackelberg博弈
1 引 言
电子商务的飞速发展,由传统零售商渠道和制造商直销渠道组成的双渠道运作模式成为流行趋势.在这种双渠道供应链管理中,一方面,信息共享是上下游之间实现协同运作的关键,高质量的信息传递与共享能够降低整个供应链的不确定性,改善供应链的服务并提高供应链的效率;另一方面,制造商开设直销渠道,引起“渠道冲突”问题[1].为了提高竞争力,越来越多的零售商开始提供产品的增值服务,如产品亲自体验、产品现场支持、产品保养服务等[2],很多实证分析[3,4]已经表明服务质量是顾客渠道选择决策的最主要影响因素之一.
信息共享是实现供应链管理的基础[5].关于信息共享问题对双渠道供应链绩效的影响已经有一些很好的成果.其中一大类是对需求预测信息的共享问题进行研究,此类均假设供应链上游和下游可以使用预测技术对市场需求进行预测,然后讨论信息共享前后的利润变化情况.如Yao等[6]以需求在直销和零售两个渠道的分配比例为预测信息,研究了双渠道下制造商如何为开设的直销渠道制定退款协议,以及预测信息共享对制定退款协议的影响.周永务等[7]研究了在不对称的需求信息情形下,如何通过数量折扣手段进行供应链协调定价的问题.Yue等[8]也研究了双渠道下“按订单生产”和“由库存发货”两种模式的需求信息共享或不共享时制造商和零售商各自的利润,求得信息的价值并讨论了零售商愿意共享其信息的条件.在Yue等[8]的研究基础上,艾兴政等[9]、陈忠等[10]均在不同情形下发展了信息共享对供应链影响的研究.进一步,Yan等[11−12]则假设制造商和零售商对顾客的保留价格进行预测,在双渠道结构下研究了多零售商之间的预测信息共享问题,讨论了信息共享对利润的影响.张菊亮等[13]在供应链纵向信息共享问题上得到了不同的结论,说明缺少相应的协调机制将使得信息共享不能增加供应链的利润.聂佳佳[14]针对预测信息分享对制造商开通直销渠道的影响进行研究,提出信息分享补偿机制可以激励零售商自愿分享其私有信息.
还有一些研究是关注零售商产品增值服务信息的共享问题.为了应对制造商开设直销渠道带来的负面影响,一些零售商对产品进行增值处理来提高其竞争力.有学者研究了其中产品增值过程中发生的成本信息共享对供应链各方利润的影响,如Yao等[15]研究了对称信息下考虑零售服务的双渠道定价问题.而Samar等[16]在Yao的基础上探讨了信息不对称的情况,并分析了服务增值信息对各方利润的影响,讨论了信息对供应链各方的价值.
目前在双渠道供应链的研究中大多数文献都假设信息是对称的,也有考虑信息不对称的情况,但研究的重点均是关注制造商是否应该开设直销渠道的问题,且一般共享的信息是顾客需求的预测信息,其余信息为共同知识.本文借鉴以上文献成果,考虑双渠道供应链中制造商已经开设了直销渠道,针对顾客需求预测信息和产品增值服务成本信息制造商和零售商同时共享和不共享两种情景,分别建立了Stackelberg博弈模型,分析了两种情景下各方定价和利润的变化情况,讨论了零售商愿意共享这两方面信息的条件.
2 问题描述

图1 混合传统渠道和电子渠道的双渠道供应链结构Fig.1 A mixed retail and direct channels of dual-channel supply chain
如图1所示,考虑含有一个开设直销渠道的制造商和一个允许对产品附加增值服务的零售商组成的双渠道供应链.制造商生产一种产品,顾客既可以通过制造商开设的直销渠道购买此产品,也可以从传统的零售渠道购买.根据文献[6,17]研究成果可知,无论零售商是强势还是弱势,制造商直销渠道的开设都会使得零售商的市场份额降低.零售商为了在渠道竞争的劣势中存活,开始为传统渠道售出的产品提供增值服务,如体验服务、产品包装服务、产品支持服务等,通过产品的增值服务来影响顾客的渠道选择.
假设制造商和零售商进行Stackelberg博弈,制造商较零售商更为强势,在决策博弈过程中占据主导位置,并有如下基本假设:1)双方策略都是对其推测对手行为的最好反应,即各决策方均为完全理性;2)双方均为风险中性;3)供应链由订单拉动需求,即各节点不考虑库存.下面分析基于以上假设的模型和基本市场结构.
2.1 需求函数和需求信息
借鉴Yue和Samar等[8,16]的研究,假设需求是关于价格的线性函数,直销渠道和传统渠道的需求函数分别表示如下:
电子渠道需求

零售渠道需求

其中Dd为制造商开设的直销渠道需求量,Dr为传统零售渠道的需求量;a是整个市场的基本需求量;θ反映了消费者偏好,表示选择在制造商直销渠道购买产品的消费者占总市场基本需求量的份额,而(1−θ)反映了偏好传统零售渠道购买产品的消费者份额,其中θ∈[0,1],θ越大表示在直销渠道购买该类型产品的消费者越多;pd、pr分别为产品在直销渠道和传统渠道的销售价格;v代表零售商提供增值服务后产品的增值; b1、b2分别为直销渠道和传统渠道的价格斜率,代表着需求对价格的敏感度;c1、c2分别为直销渠道和零售渠道的交叉价格弹性系数,表示一个渠道产品价格对另一个渠道需求影响的敏感度.假设bi>ci,i=1,2,即某一渠道价格对自身渠道需求的影响比另一渠道价格对需求的影响大.为方便分析,且不影响最后的结论,假设c1=c2=e.
考虑到市场需求受经济和商业的影响,具有不确定性.假设基本需求量a为随机变量,令a=+ξ,其中为市场需求a的均值,ξ服从均值为0、方差为的正态分布.制造商和零售商均利用市场信息收集技术对未知需求进行预测.定义制造商和零售商对基本需求a的预测值分别为fm和fr,并假设fm=a+ξm, fr=a+ξr.其中ξm和ξr是独立于a,且服从均值为0、方差分别为和的正态分布,其值变化越大说明预测精度越小.预测误差ξm和ξr是相关的,相关度的高低取决于双方在预测过程中采用的数据和方法.双方采用的数据和方法越相似,将越有可能导致预测值的高相关性.相关矩阵为

假设协方差不大于方差,即ρσmσr6,ρσmσr6.基于Winkler[18]的研究,在各预测值条件下a的期望及相关表达式如下

式(4)表示在fi预测值下,基本需求a的期望值,记aM=E[a|fm]为制造商基于自身预测值fm下a的期望值,同时记aR=E[a|fr]为零售商基于自身预测值fr下a的期望值.式(5)中,aI为信息共享后同时基于fm、fr预测值下a的期望值.式(6)的E[fr|fm]为制造商以预测值fm为条件对零售商的预测值fr进行推测得到的期望值.将E[fr|fm]代入式(5)可得式(7),aIM为信息共享前制造商以fm为条件模拟的信息共享情况下a的期望,化简式(7),容易得到aIM=aM,因此下文的模型中均以aM代替aIM.本文不考虑信息收集和预测过程中产生的成本.
2.2 产品附加增值服务的成本函数
这里考虑零售商对销售的产品进行附加增值服务.假设零售商为产品增值v单位的价值时,将产生c(v)的服务成本.基于Yao和Samar等[15,16],可以定义该服务成本为c(v)=ηv2/2,其中η表示零售商实施增值服务产生的成本效率参数,是零售商的私有信息.在产品增值成本信息共享情形下,制造商被告知η的精确值.在产品增值成本信息没有共享情形下,制造商不知道η的精确值,但已知随机变量η服从[−α,+α]区间内均值为的均匀分布.
假设所有参数均大于零,则制造商和零售商可共享的信息有需求预测信息和增值服务成本信息.模型中的所有参数,除了这两部分信息的预测值外,都是双方的共同知识.这里假设产品增值成本信息和市场需求信息的预测过程是不相关的,即Cov(ξi,)=0,i=r,m.博弈之前双方首先对是否共享这些信息达成协议,然后作为主方的制造商根据可以使用的信息制定批发价格和直销渠道价格,最后零售商根据制造商公开的定价策略,决策其自身的零售价格和服务增值价值.
3 模型建立和决策分析
基于前面定义的参数,制造商和零售商进行决策以使自己利润达到最大的定价策略,利润函数分别为
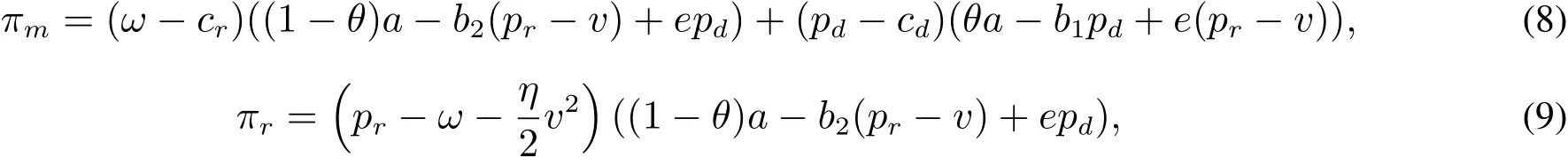
其中πm和πr分别代表制造商和零售商的利润;ω代表制造商制定的批发价格,为防止零售商以更低的价格从直销渠道购买产品,假设批发价ω不高于直销价格pd,即ω6pd;式中cr、cd分别为传统零售渠道和直销渠道中单位产品的边际成本.为区分以下分别出现的两种情形,本文用上标S、NS分别表示零售商共享、不共享其增值成本信息;下标I、NI分别表示零售商共享、不共享其需求预测信息.
由于制造商为Stackelberg博弈主方,先根据其预测信息制定批发价格,因此零售商完全可以根据批发价格推断出fm的值[5],进而同时利用双方预测值fm和fr制定其定价决策,这是从方相对主方滞后决策而获得的优势.以下分析均基于此信息优势,即零售商始终利用双方信息制定决策,而制造商也清楚这一点.
3.1 信息完全共享的情形
在信息完全共享的情形下,零售商将产品增值成本信息和市场需求预测信息同时与制造商分享,此时供应链双方的期望利润均基于双方共同的预测信息.在信息完全共享情形下,零售商和制造商的利润函数分别为
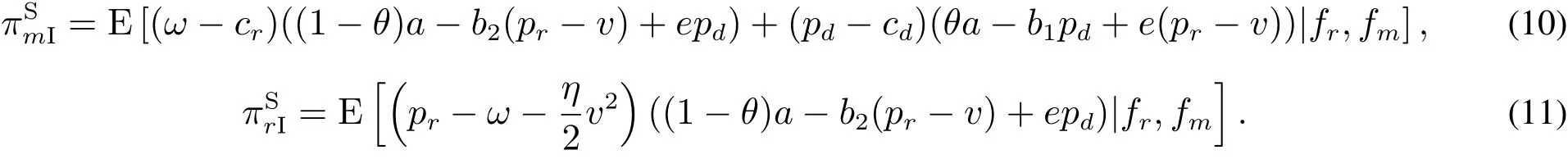
基于Stakelberg主从博弈模型,可得到下列结论.
命题1 需求预测信息和产品增值成本信息完全共享的情形下,制造商和零售商的最优策略如下
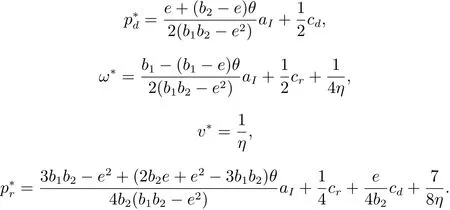
制造商和零售商各自的最大利润分别为
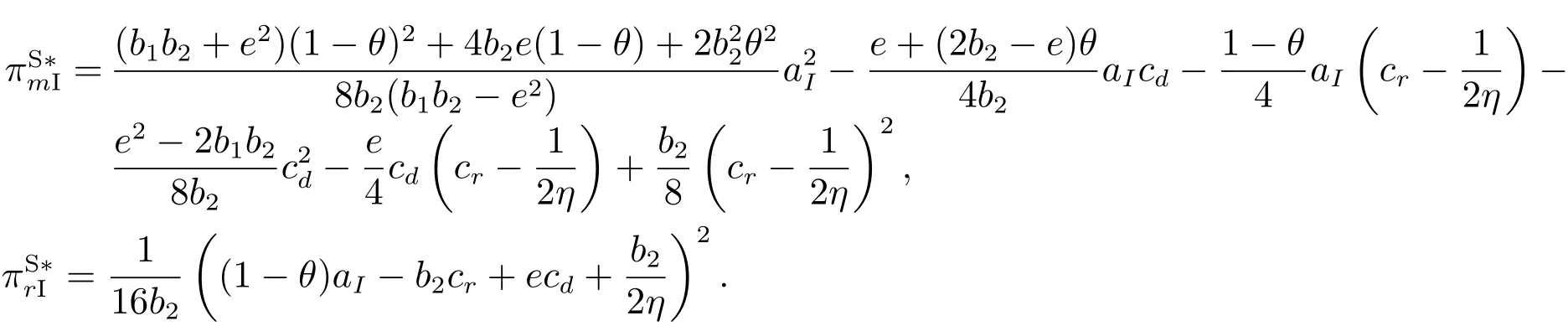
从命题1可以看出,pd、pr和ω均是市场基本需求量a的增函数,需求量越大,则制定的价格越高,而产品附加价值只和零售商增值成本系数η相关,不受其它参数影响,且直销渠道价格pd也不受传统渠道的服务增值价值v的影响.下面将进一步讨论信息完全不共享的情形.
3.2 信息完全不共享的情形
在信息完全不共享的情形下,零售商既没有同制造商分享其产品增值的成本信息,也没有共享其预测信息.根据前文的讨论,在预测信息不共享情形下零售商仍能够根据双方的预测信息制定决策,而制造商只能根据自身预测值fm制定批发价格和直销价格.而对于没有共享的产品增值的成本信息,制造商事先不知道η的精确值,但知道η是均匀分布在[−α,+α]内的随机变量.
此时,双方为了各自利润的最大化制定价格决策,制造商和零售商的利润函数分别为
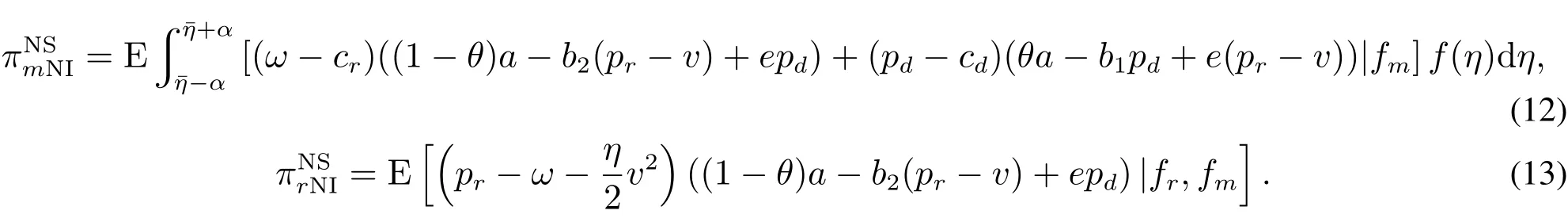
基于(12)、(13)两式,可得下列结论
命题2 产品增值成本信息和市场预测信息均没有共享的情形下,制造商和零售商的最优策略如下
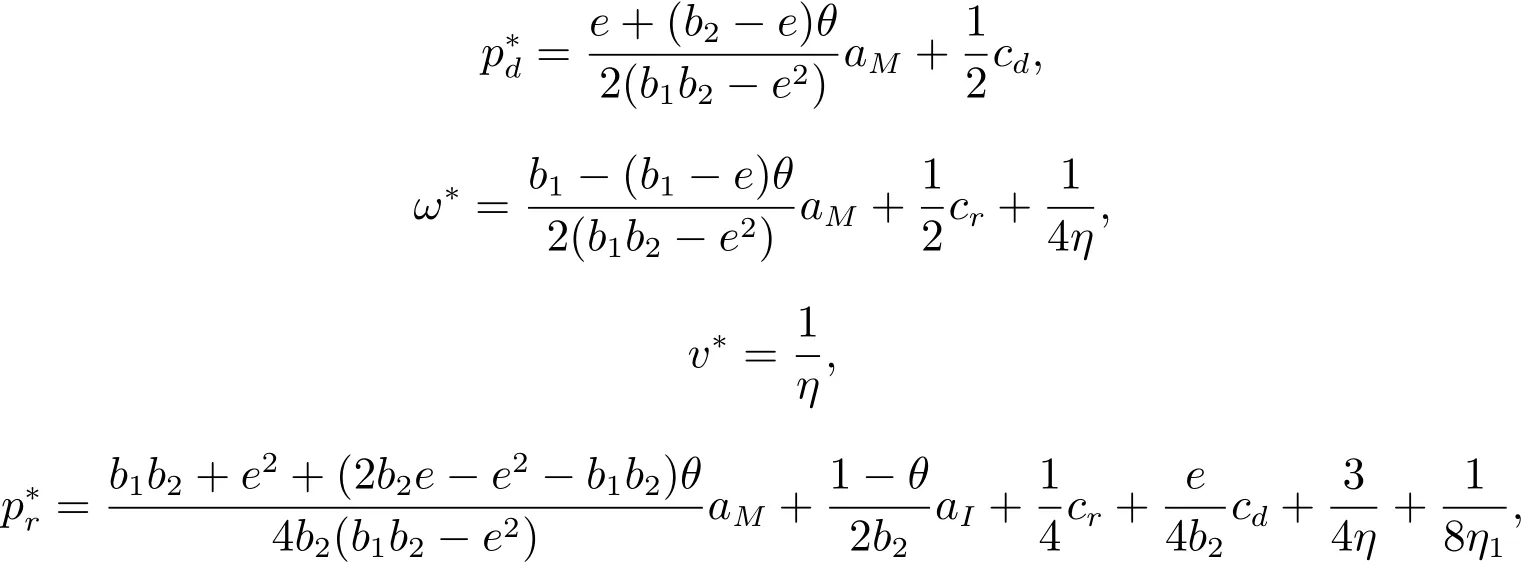
此时制造商和零售商的最大利润分别为
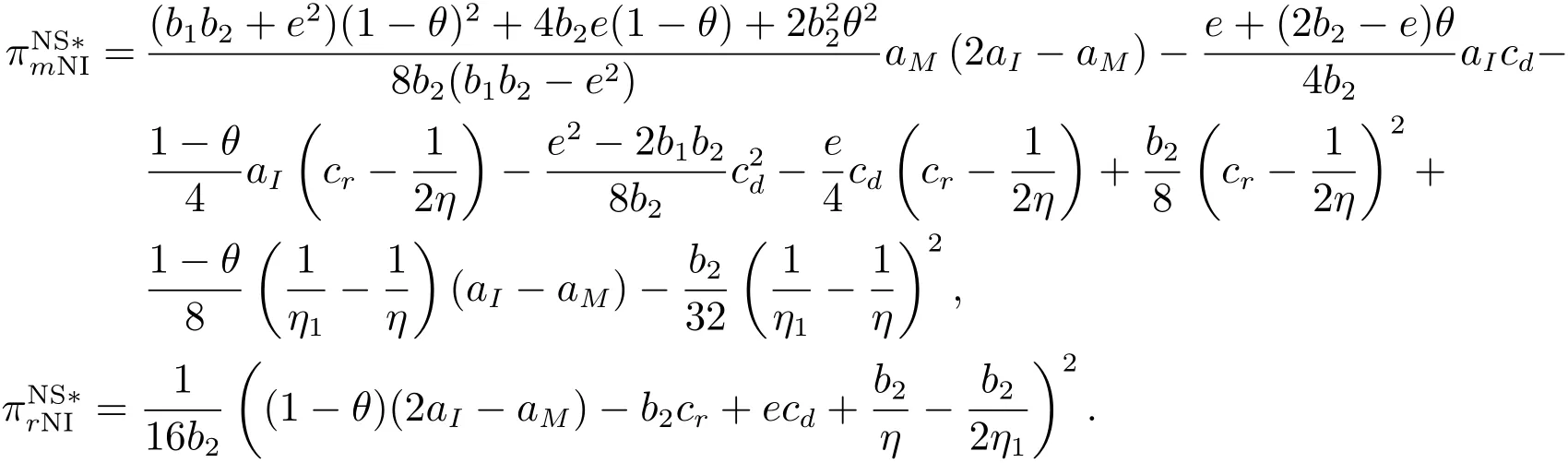
由命题2可以看出,零售渠道的增值成本信息共享与否不影响直销渠道的最优价格和产品附加价值,但预测信息的共享会影响制造商定价.此外,零售商自身制定的零售价格会随制造商对需求预测及成本估计的大小产生波动.
在命题2得到的结论中,存在两种特殊的情形:当aI=aM、时,制造商和零售商只共享了需求预测信息;当、η=η1时,制造商和零售商只共享了服务增值成本信息.这两种情形分别对应文献[8]和文献[16]中单一信息不对称的情形,而本文重点讨论与现实更相近的一般情形,即、的情况,是对以上文献研究的一般性扩展.
4 信息共享价值分析
由命题1和命题2容易比较得出两种情形定价和利润的不同.比较信息共享前后决策变量的差值,可得下列结论.
命题3 信息共享后批发价、直销价和零售价格等决策变量的增值分别为
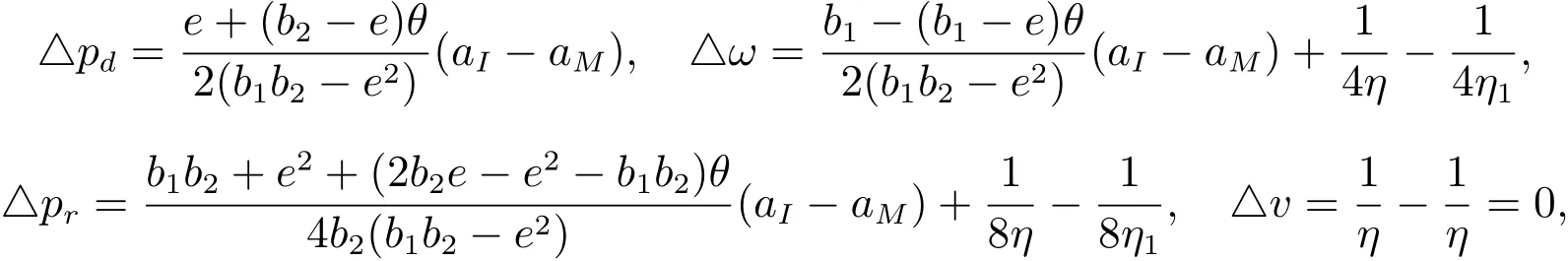
由△v=0可知信息共享对零售商的服务增值决策没有影响.
命题3可以看出:1)在直销渠道,制造商制定直销价不受零售商服务增值决策的影响,直销价格的变化由aI、aM(即fr和E[fr|fm]的大小决定;2)在零售渠道,批发价格和零售价格的变化同时由aI、aM和η、η1的大小决定,哪部分信息占更大的权重视系数取值而定.
比较两情形的利润可以得到完全共享两种信息对制造商的价值为
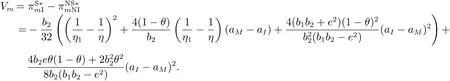
因为bi>e>0,i=1,2,因此b1b2+e2>b1b2−e2.可知只要或成立,则满足

由式(14)可以看出,只要制造商没有同时对零售商的两部分私有信息做出完美预测(E[fr|fm]= fr且η1=η),信息共享就会为制造商带来正的价值.
同理,完全共享两种信息对零售商的价值为

可知当且仅当满足

时,Vr>0,即完全共享信息会使零售商增加利润.因为容易证明

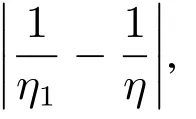
由命题1,2和式(11)、(13),可得结论
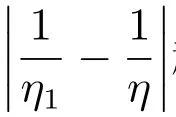
命题4的结论很直观,即估计值与实际值相差越远,信息的价值便愈加显现.这一点同其他信息共享的研究结论相一致.正如前文所述,信息不共享情形下零售商仍将持有完全的信息,因此对信息共享的积极性并不高,甚至会因信息的共享导致利润受损.这种情形下,制造商应该采取激励机制,转移部分利润以刺激零售商主动共享其信息.
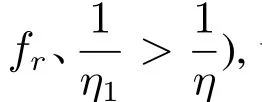
为了更直观的分析利润变化情况,本文利用Mathematica模拟数值算例,进行进一步分析验证,使研究成果更具管理意义.各参数取值为=250,θ=0.3,b1=b2=2,e=1,cr=cd=10,σ0=15,σm= 15(0−30),σr=15(0−30),=0.2,α=0.06.为简化计算的复杂性,令ρ=0.根据式(15)的条件利用Mathematica作图如下所示:
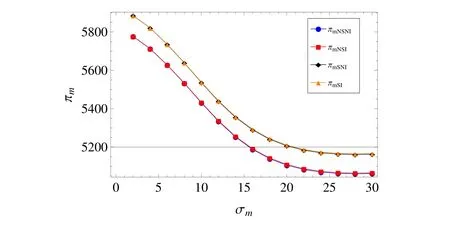
图2 制造商预测精度σm对制造商利润的影响Fig.2 Impact of manufacturer’s forecast accuracy σmon manufacturer’s proft

图3 制造商预测精度σm对零售商利润的影响Fig.3 Impact of manufacturer’s forecast accuracy σmon retailer’s proft
其中下标NSNI和NSI分别表示无服务时信息不共享、信息共享情况;下标SNI和SI分别表示考虑服务的供应链中信息不共享、信息共享情况.
由图2和图3可以看出,双渠道供应链下,随着制造商对市场信息预测精度降低,双方的利润均降低;考虑服务的供应链利润相对较高;同时,在满足不等式(15)的条件下,信息共享能够为制造商和零售商都带来收益.零售商的预测精度影响的实验结果与之类似,在此不再累述.
5 结束语
本文假设考虑的供应链由开设了直销渠道的制造商和允许对产品附加增值服务价值的零售商组成,其中需要共享的信息包括双方各自持有的市场预测信息和产品增值服务成本信息两部分,利用Stackelberg主从博弈理论建立了问题模型,分别求解了两种信息完全对称和完全不对称情形下制造商和零售商的最优定价决策和最大期望利润,并分析了两种信息的共享对制造商和零售商利润的影响和价值,同时也给出了双方自愿共享私有信息的条件,为供应链中的决策者进行信息共享决策问题提供了理论基础.本文还可以考虑制造商和多个零售商信息共享下的协调机制问题,这是进一步研究的方向.
[1]Chiang W K,Chhajed D,Hess D J.Direct marketing,indirect profts:A strategic analysis of dual-channel supply-chain design[J]. Management Science,2003,58(12):1–20.
[2]Hu Wei,Li Yongjian.Retail service for mixed retail and E-tail channels[J].Annals of Operations Research,2012,192(1):151–171.
[3]Devaraj S,Fan M,Kohli R.Antecedents of B2C channel satisfaction and preference:Validating E-commerce metrics[J].Information Systems Research,2002,13(3):316–333.
[4]Rohm A J,Swaminathan V.A typology of online shoppers based on shopping motivations[J].Journal of Business Research,2004, 57(7):748–757.
[5]陶文源,寇纪淞,李敏强.信息共享对供应链的影响[J].系统工程学报,2002,17(6):486–490.
Tao Wenyuan,Kou Jisong,Li Minqiang.Effect of information sharing on supply chain[J].Journal of Systems Engineering,2002, 17(6):486–490.(in Chinese)
[6]Yao Dongqing,Yue Xiaohang,Wang Xiaoyin,et al.The impact of information sharing on a return policy with the addition of a direct channel[J].International Journal of Production Economics,2005,97(2):196–209.
[7]周永务,杨善林.基于不对称需求信息的供应链协调定价[J].系统工程学报,2006,21(6):591–597.
Zhou Yongwu,Yang Shanlin.Pricing coordination in supply chain based on symmetric demand information[J].Journal of Systems Engineering,2006,21(6):591–597.(in Chinese)
[8]Yue Xiaohang,Liu John.Demand forecast sharing in a dual-channel supply chain[J].European Journal of Operational Research, 2006,174(1):646–667.
[9]艾兴政,唐小我,马永开.传统渠道与电子渠道预测信息分享的绩效研究[J].管理科学学报,2008,11(1),12–23.
Ai Xingzheng,Tang Xiaowo,Ma Yongkai.Performance of forecasting information sharing between traditional channel and E-channel[J].Journal of Management Sciences in China,2008,11(1):12–23.(in Chinese)
[10]陈 忠,艾兴政.双渠道信息共享与收益分享合同选择[J].系统工程理论与实践,2008,28(12):42–50.
Chen Zhong,Ai Xingzheng.Choice of forecasting information sharing and revenue sharing contract between dual-channel[J].Systems Engineering:Theory and Practice,2008,28(12):42–50.(in Chinese)
[11]Yan Ruiliang,Ghose S.Forecast information and traditional retailer performance in a dual-channel competitive market[J].Journal of Business Research,2010,63(1):77–83.
[12]Yan Ruiliang,Pei Zhi.Information asymmetry,pricing strategy and frm’s performance in the retailer-multi-channel manufacturer supply chain[J].Journal of Business Research,2011,64(4):377–384.
[13]张菊亮,章祥荪.供应商和销售商拥有部分信息的信息共享[J].中国管理科学,2012,20(1):109–116.
Zhang Juliang,Zhang Xiangsun.Information sharing in a supply chain with supplier and retailer’s partial information[J].Chinese Journal of Management Science,2012,20(1):109–116.(in Chinese)
[14]聂佳佳.预测信息分享对制造商开通直销渠道的影响[J].管理工程学报,2012,26(2):106–112.
Nie Jiajia.The effect of forecast information sharing on manufacturer’s launching direct channels[J].Journal of Industrial Engineering and Engineering Management,2012,26(2):106–112.(in Chinese)
[15]Yao Dongqing,Liu John J.Competitive pricing of mixed retail and e-tail distribution channels[J].Omega:International Journal of Management Sciences,2005,33(3):235–247.
[16]Samar K,Mukhopadhyay,Yao Dongqing,et al.Information sharing of value-adding retailer in a mixed channel hi-tech supply chain[J].Journal of Business Research,2008,61(9):950–958.
[17]浦徐进,石 琴,凌六一.直销模式对存在强势零售商零售渠道的影响[J].管理科学学报,2007,10(6):49–56.
Pu Xujin,Shi Qin,Ling Liuyi.Effect of direct marketing on retailing channels where large retailers exist[J].Journal of Management Sciences in China,2007,10(6):49–56.(in Chinese)
[18]Winkler R.Combining probability distributions from dependent information sources[J].Management Science,1981,27(4):479–488.
Information sharing value in dual-channel supply chain
Li Bo,Sun Peng,Li Qinghua
(College of Management&Economics,Tianjin University,Tianjin 300072,China)
This paper assesses the impact of sharing multi-information on pricing and performance when a direct channel is involved.We consider a manufacturer-retailer supply chain,which consists of a direct channel opened by the manufacturer and a traditional retail channel which is allowed to add value to the product.Both the manufacturer and the retailer perform their own forecasts based on the primary demand.The retailer holds the cost of adding value as private information.The manufacturer is assumed to be the Stackelberg leader,and two scenarios are analyzed:under the complete information and the completely unknown information on the demand forecast and value add services.The paper fnds that information sharing always has a positive impact on the manufacturer’s performance,and the retailer would be motivated to share its private information with the manufacturer under some conditions.
supply chain management;dual-channel;value of information;Stackelberg game
TP273
A
1000−5781(2015)04−0530−09
10.13383/j.cnki.jse.2015.04.010
2013−01−16;
2013−07−15.
高等学校博士学科点专项科研基金资助项目(20100032110034);教育部人文社会科学研究规划基金资助项目(12YJAZH052);国家自然科学基金资助项目(71472133).
book=538,ebook=109
李 波(1967—),女,山西长治人,博士,教授,博士生导师,研究方向:供应链协调与优化,E-mail:libo0410@tju.edu.cn;
孙 鹏(1987—),男,辽宁鞍山人,硕士生,研究方向:信息不对称下供应链协调研究,Email:sunpeng 871019@163.com;
李庆华(1987—),女,山东烟台人,博士生,研究方向:考虑行为影响的供应链协调与优化,Email:liqinghua@tju.edu.cn.
