中国商业财产保险欺诈损失度量实证研究

林 源,李连友

(1.湖南大学金融与统计学院,湖南长沙410082; 2.怀化学院经济系,湖南怀化418008)

中国商业财产保险欺诈损失度量实证研究

林 源1,2,李连友1

(1.湖南大学金融与统计学院,湖南长沙410082; 2.怀化学院经济系,湖南怀化418008)

应用贝叶斯马尔科夫链蒙特卡洛(MCMC)方法估计参数,采用分段定义损失强度的损失分布法(PSD-LDA),测算了财产保险欺诈风险潜在损失TailVaR、经济资本和纯保费,并同超阈值(POT)方法、单一损失分布法等度量结果进行了比较.研究发现,财产保险欺诈损失尾部风险很大,PSD-LDA方法度量财产保险欺诈损失较为合理,为我国保险产品定价和保险欺诈风险管理决策提供理论依据.

保险欺诈;广义Pareto分布;Gibbs抽样;经济资本

1 引 言

中国保险业经过30年多年的快速增长,已经成为国民经济的一个重要支柱.2013年全年实现保费收入1.72万亿元,同比增长11.2%,比上年提高3.2个百分点.其中,财产险保费收入6 212亿元,同比增长16.5%1数据来源于中国保监会网站统计数据,http://www.circ.gov.cn/web/site0/tab5201/..不过,随着保险业的快速发展,我国保险欺诈案件不断出现.2012年3月以来,保险欺诈报案1千余次,涉案金额1.6亿多元;全国保险诈骗立案1 300余件,破案近1 100起,处罚500余人.保险欺诈已引起监管部门的高度重视.《欧盟偿付能力II》和《中国第二代偿付能力监管制度体系建设规划》中明确要求建立以风险度量为基础的偿付能力监管体制,并要求计算操作风险资本需求.2012年8月6日保监会又发布了《关于加强反保险欺诈工作的指导意见》,要求对保险欺诈风险进行计量.因此,研究我国商业保险欺诈风险度量问题非常必要.

保险欺诈是指“保单持有人可能不如实报告他们损失的大小,或报告一个从未发生的事故;保单持有人签订保单时,没有如实告知相关信息也可能存在欺诈;或故意扩大损失,以扩大索赔.”[1]《欧盟偿付能力II》指出,欺诈是保险操作风险中的一种,包括内部欺诈和外部欺诈.内部欺诈主要指故意的不良行为(如雇员盗窃、虚构索赔等),外部欺诈指未授权的交易活动(如欺诈索赔、伪造索赔资料)等.我国保监会指出,保险欺诈是指利用或假借保险合同谋取不法利益的行为[2].

目前学界对于保险欺诈风险的度量研究还比较缺乏,保险操作风险度量的研究仍然处于起步阶段,主要借鉴银行操作风险度量方法来研究.Tripp等[3]探讨了极值理论(Extreme Value Theory)在非寿险行业操作风险度量的应用,认为模型的参数估计非常关键.Dexter等[4]在Tripp等的研究基础上,借鉴《巴塞尔II》,进一步研究了损失分布法等方法在寿险公司操作风险资本计量中的应用,并构建了操作风险资本评价框架.因数据缺乏,这些研究仅是理论探讨,缺乏实证分析.Paudel[5]采用损失分布法、贝叶斯方法度量保险公司的操作风险,并发现保险操作风险的厚尾特征.Lambrigger等[6]在《巴塞尔II》和《欧盟偿付能力II》的框架下,用贝叶斯方法计算保险操作风险VaR和ES.Perez[7]根据《欧盟偿付能力II》,应用极值理论和VaR方法估算了西班牙两家保险公司汽车责任保险偿付能力资本要求.Bolance等[8]以VaR为工具,采用非参数方法度量汽车保险外部欺诈损失.Morales等[9]用损失分布法和蒙特卡洛模拟法估算哥伦比亚保险行业汽车欺诈风险(盗窃)损失VaR值及偿付能力资本要求.另外,针对极值风险的度量,周孝华等[10]提出基于EVT-POT-SV-GED的动态VaR模型.由于EVT存在只能测量低频高损事件而忽略高频低损事件损失的缺陷,为了测度全面的风险资本,King[11]应用Delta-EVT法综合测量高频低损与低频高损事件的损失VaR,有效弥补了GPD的缺陷.Li[12]采用PSD-LDA法度量银行操作风险资本,与基本指标法比较,发现PSD-LDA法较优.针对保险巨额损失,王丽珍等[13]利用VaR等方法提出基于偿付能力的最优保险策略.前述文献对风险度量的研究主要以VaR方法为主,而VaR方法不满足风险度量一致性原则,而且未考虑超过VaR水平的尾部风险[14],因而存在一定的不足.目前国内对保险欺诈的定量研究主要集中在应用信息经济学理论分析保险欺诈行为[15,16],实证研究主要是利用数据挖掘技术识别保险欺诈索赔行为[17,18],尚未见到有关我国保险欺诈风险度量的研究.

本文在前述研究的基础上,运用分段定义损失强度分布的损失分布法(PSD-LDA)和满足风险度量一致性原则的TailVaR(以下简称TVaR)方法计量我国商业财产保险欺诈风险及其经济资本.考虑到样本较小,引入基于Gibbs抽样的Bayesian MCMC(Markov chain Monte Carlo)方法估计参数.

2 财产保险欺诈损失度量模型

首先假定:欺诈风险损失频率和损失强度相互独立;不同类型的欺诈风险损失强度相互独立,即高频低损欺诈损失与低频高损欺诈损失相互独立.

2.1 损失频率分布

在损失分布法中,通常假定操作风险事件发生频率服从Poisson分布、负二项分布或二项分布.由于不同的损失强度分布导致损失值产生较大差异,而不同损失频率分布对损失值的影响无显著差异[19].因此,假定财产保险欺诈风险损失事件发生频率服从Poisson分布.

如果每年欺诈风险发生次数N服从Poisson分布,则有Pr(N=n)=e−λλn/n!.其中λ可以通过每年发生次数的均值估计.Leadbetter等[20]证明,对于足够大的阈值u,超额数X序列逐渐收敛于一个强度为λu(λu>0)的泊松过程.因此假定高频低损的欺诈风险损失频率服从Po(λ1),低频高损欺诈风险损失频率服从Po(λ2),那么每年欺诈风险损失频率服从Po(λ1+λ2),即有

参数λ1、λ2可以分别通过阈值u之下和之上每年发生欺诈次数的均值获得.

2.2 损失强度分布

财产保险欺诈损失具有“高频低损”和“低频高损”的特征(见第3部分),因此采用两阶段分布模型拟合.即在选取合适的阈值后,阈值右侧的低频高损数据用广义Pareto分布(GPD)拟合,阈值左侧的高频低损数据用对数正态分布拟合.于是财产保险欺诈损失分布为

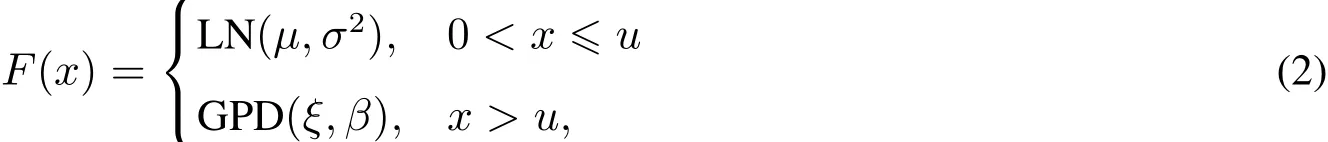
其中对数正态分布密度函数为

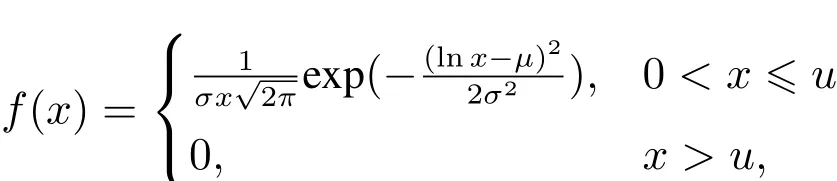
广义Pareto分布密度函数为

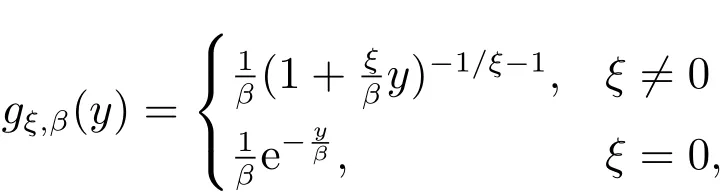
其分布函数为

这里y=x−u,β>0为尺度参数.当ξ>0时,y>0;当ξ<0时,06y6−β/ξ.ξ为形状参数,当ξ>0时,GPD是厚尾的;ξ=0时,为指数分布;ξ<0时为薄尾型的Pareto分布.

在式(2)中,阈值u的选取非常关键.选取过高,会导致超额数据过少,参数估计的方差很大;选取过低,则不能保证超额分布收敛,导致估计产生较大偏差.阈值u的选取采用超额均值函数(mean excess function, MEF)方法.

对于给定的样本,样本超额均值函数的定义为

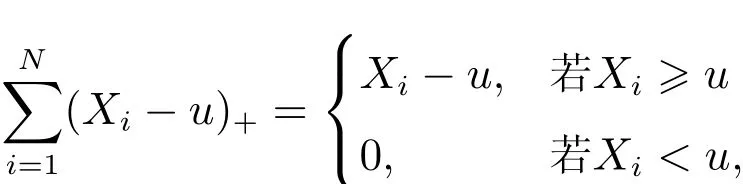
其中Nu表示超过阈值的样本个数.当阈值充分大时,点(u,e(u))构成的曲线e(u)近似线性.当x>u时, e(u)斜率为正,说明数据遵循形状参数为正的GPD.据此选取恰当的阈值,使得当x>u时,为近似线性函数且向上倾斜,说明数据遵循厚尾的GPD.

阈值选取后,对于阈值之上的低频高损数据,用广义Pareto分布拟合.为解决低频高损数据不足带来的误差,使用基于Gibbs抽样的贝叶斯MCMC方法估计GPD的参数(见文献[21]),本文采用Openbugs软件计算.因高频低损部分样本数据相对较多,故对数正态分布的参数估计采用极大似然方法.

2.3 财产保险欺诈损失的纯保费估计

理论上,纯保费等于期望年索赔额.设SN为某个时期内(年)总欺诈索赔额,N是该期内的欺诈索赔次数,Xi表示第i次欺诈索赔额,N,X1,X2,...,XN是相互独立的随机变量,且X1,X2,...,XN具有相同分布,则有

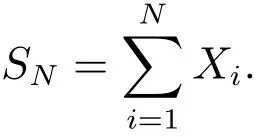
于是,财产保险欺诈损失纯保费为

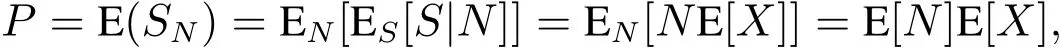
即保险欺诈损失纯保费等于年欺诈索赔次数的均值和欺诈索赔额均值的乘积.结合式(1)和式(2),有

2.4 财产保险欺诈损失度量

采用PSD-LDA方法度量财产保险欺诈损失.在得到财产保险欺诈损失频率和损失强度分布函数后,总损失分布通过蒙特卡洛模拟实现,具体步骤见文献[22].本文采用Matlab R2012b计算,模拟10 000次,得到各置信水平下的VaR、TVaR估计值,取其估计值的10次均值作为最终估计结果.

另外,根据PSD-LDA方法计算得到VaR、TVaR估计值后,可将其与极值理论的POT模型等的计算结果进行比较.根据文献[23],设X为一随机损失变量,u为一阈值(一般较大),则超额损失X−u近似服从广义帕累托分布.给定置信水平α,于是有

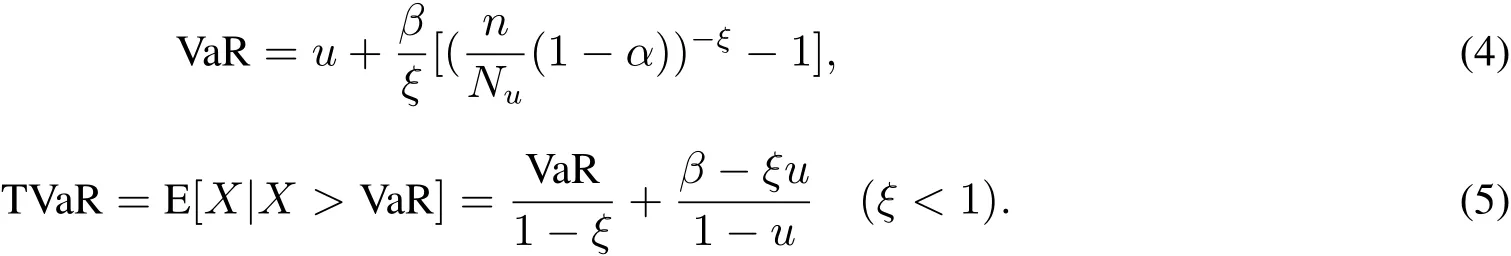
《欧盟偿付能力II》建议用置信水平99.5%、时间周期为1年的VaR值来计量保险操作风险偿付能力资本要求(SCR).考虑到VaR的不足及“欺诈暗数”的存在,为了稳健,选取置信水平99.9%、时间周期为1年的TVaR值来计提财产保险欺诈风险经济资本.

3 实证分析

3.1 数据描述分析

目前国内还没有保险欺诈损失数据库,因此,从“中国保险网”等媒体公开报道中收集保险欺诈损失事件1见:中国保险网-保险案例-保险与欺诈,http://www.china-insurance.com/case/..按照欺诈(案发)时间、涉案险种、损失金额、欺诈主体及类型等内容进行整理,得到1989–2012年间财产保险欺诈损失数据178个.通过对损失数据进行分析,可以了解目前我国财产保险欺诈现状:

1)从涉案险种来看:机动车保险占74.3%,货运险、企财险和责任险等占25.7%;

2)从欺诈类型来看:隐瞒标的信息占4.3%,夸大损失占4.8%,虚构保险事故占37.1%,故意制造保险事故占47.0%.可见,财产保险欺诈以故意制造保险事故和虚构保险事故为主;

3)从欺诈主体来看:投保方欺诈占51.6%,团伙职业性欺诈占34.8%,内部职员欺诈占10.1%;

4)从损失结果来看:车损险欺诈导致财险欺诈损失55.7%,企财险、货运险和责任险等共占44.3%.外部欺诈导致损失占84.5%(其中团伙职业性欺诈占63%(主要针对车损险),投保方欺诈占21.5%),内部欺诈(职员及代理人)致损15.5%.可见,财产保险欺诈损失主要是外部欺诈造成;

5)损失数据的特征:受保险金额的限制,每次欺诈造成的损失有限,欺诈呈现“低损失”的特点.由于职业性欺诈团伙通过故意制造或虚构大量保险事故骗取保险金,欺诈次数具有“高频”特点,因此保险欺诈损失

具有“高频低损”特征.另外,和保险相关的假机构、假保单、假赔案、贪污保费或退保费以及利用保险单证进行合同诈骗、非法集资等保险欺诈行为,由于脱离了保险公司核保、理赔环节的控管,不受保险金额的限制,尽管相对于前一种情况这些欺诈行为发生频率很低,但其造成的损失相当严重,损害巨大,因此财产保险欺诈又呈现“低频高损”的特征.

考虑到1989–2000年间欺诈损失数据较少(损失数据11个,共损失986.8万元),因此,应用模型分析时主要采用2001–2012年的数据共167个.财产保险欺诈损失数据及强度描述见表1、表2.

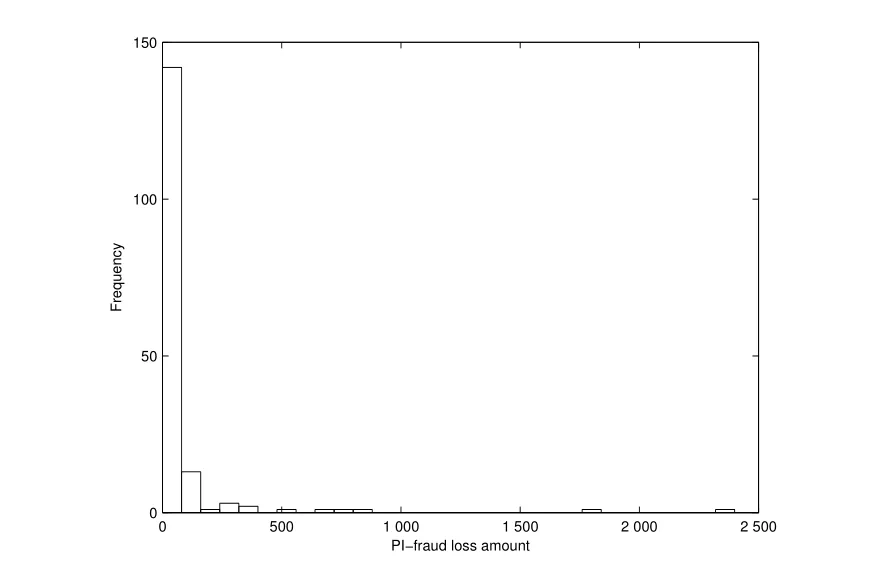
图1 欺诈损失金额直方图Fig.1 Histogram of fraud loss

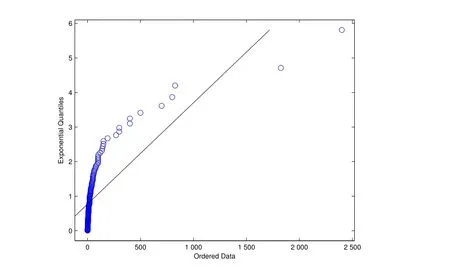
图2 Q-Q图Fig.2 Q-Q fgure

表1 财产保险欺诈损失数据1为了简化,没有考虑通货膨胀等因素,即未对数据进行折算,以当年报道的实际发生的金额为准.Table 1 Property insurance fraud loss data

表2 财产保险欺诈损失强度描述Table 2 Property insurance fraud losses severity description

由表2,偏度系数远大于0,峰度系数远大于3.可以初步判断,财产保险欺诈损失分布为尖峰厚尾分布.图1给出了损失金额直方图,图2是经验分布指数QQ图.从图1和图2可看出损失数据存在严重的厚尾现象.

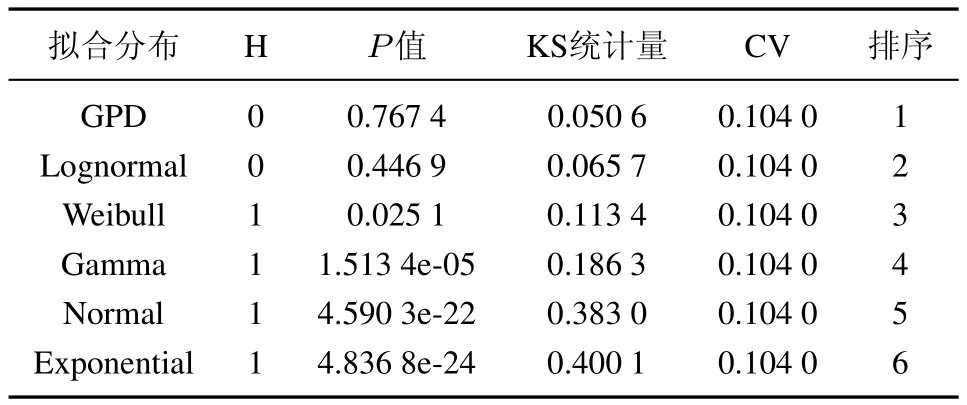
表3 财产保险欺诈损失强度分布拟合(显著性水平5%)Table 3 Property insurance fraud losses severity distribution ftting

遵循一般方法,用Lognormal、Weibull、Gamma、Exponential、广义Pareto等分布直接拟合财产保险欺诈损失数据,参数估计都采用极大似然方法,并用KS法对拟合效果进行检验(见表3).

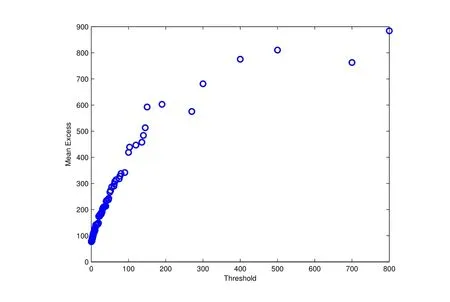
图3 超额均值函数图Fig.3 Mean Excess Function fgure

图4 Hill图Fig.4 Hill fgure

由表3可知,K-S检验拒绝了数据呈正态分布的假设,只有广义帕累托分布和对数正态分布的拟合通过检验.因此,采用分段定义来拟合欺诈损失分布,即用对数正态分布拟合高频低损数据,GPD拟合低频高损数据.

3.2 财产保险欺诈损失分布的拟合

首先,根据超额均值函数图结合Hill图来选取阈值.

从超额均值函数图(图3)可以看出,阈值在75以后图形近似线性并向上倾斜;Hill图(图4)显示在超额数27附近时Hill图开始稳定.结合来看,选择阈值u=75,对应超额数为27个.

其次,估计参数并检验.给定阈值,用基于Gibbs抽样的贝叶斯MCMC模拟法得到GPD参数估计,结果见表4.表4中还给出其他阈值及极大似然法参数估计(MLE)结果以进行比较.

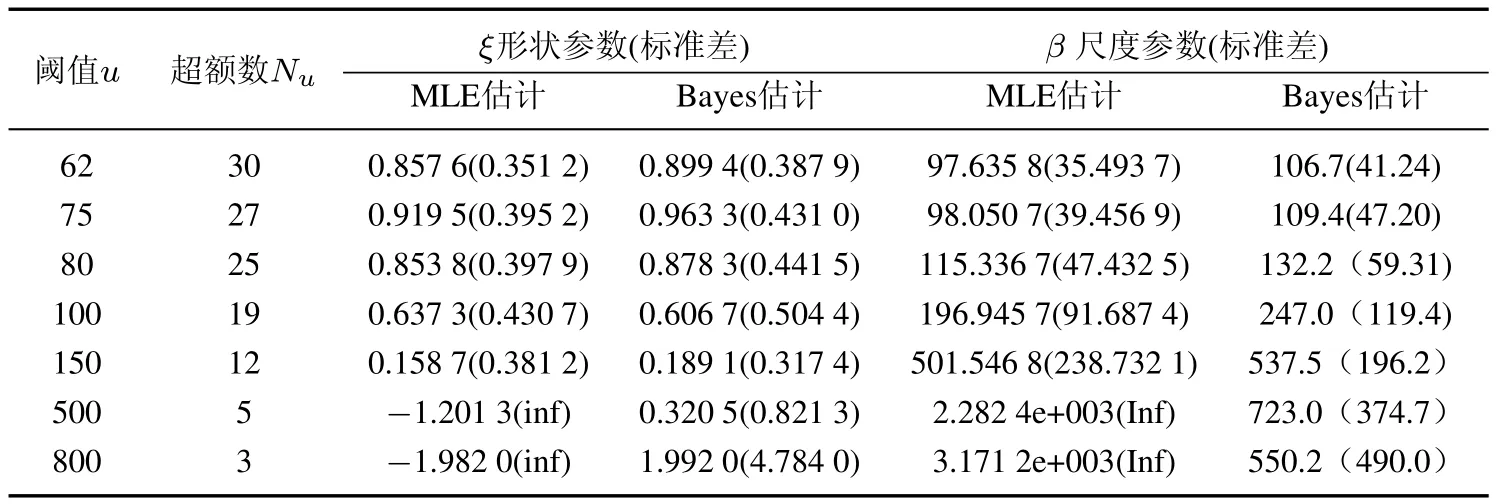
表4 GPD参数估计1说明:使用Openbugs软件进行10万次迭代,滤去前2万次,将剩下的8万次作为目标后验分布的样本,得到参数估计值.Table 4 GPD parameter estimation

由表4可知:第一,Bayes方法和MLE方法得到的参数估计值比较接近,但略大于MLE方法的结果,标准差也较大.这是由于Bayes方法中把参数看成了随机变量,增加了模型的不确定性的结果,因而更加符合实际情况[24];第二,当超额数小于5个时,形状参数的MLE估计值变为负数,已经背离了厚尾特性.说明在小样本的情况下,贝叶斯MCMC方法的估计结果明显优于MLE方法,因此选用贝叶斯方法估计GPD参数.

在得到GPD参数估计值后,对阈值u=62,u=75,u=80对应的低频高损数据是否服从广义Pareto分布进行KS检验,检验的P值分别为0.086 0,0.086 6,0.080 7,均大于0.05,其中u=75对应的P值0.086 6最大.综合考虑,选取u=75(对应超额数Nu=27)作为阈值.此时,超额数个数占样本总数的16.2%左右,满足阈值选取对应超额数占样本总数10%左右的要求[25].

另外,u=75时,从其GPD拟合图(图5)、残差的指数QQ图(图6)看,拟合的效果较好,进一步验证了阈值选取的正确性.

图5 GPD分布拟合图Fig.5 Generalized Pareto distribution ftting fgure

图6 残差指数Q-Q图Fig.6 Residuals Index Q-Q fgure

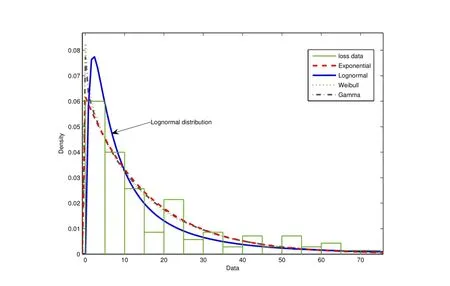
图7 欺诈风险损失拟合分布图Fig.7 Fraud loss distribution ftting fgure

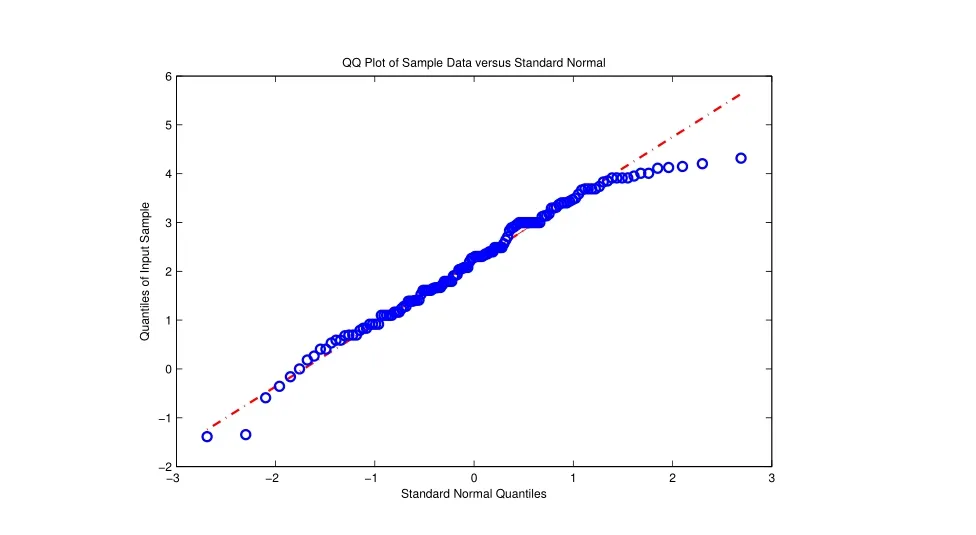
图8 Q-Q图Fig.8 Q-Q fgure

最后,拟合高频低损分布函数.针对高频低损序列,即阈值左侧x675的140个样本数据,用指数分布、伽马分布、对数正态分布、Weibull分布等进行拟合,拟合分布见图7,拟合检验结果见表5.

表5 拟合分布K-S检验结果Table 5 Results of K-S test of Fitting distributions

由表5可知,对数正态分布的拟合效果最优(p=0.323 3).图8Q-Q图（已取对数）显示对数正态分布拟合效果较好.因此,选择对数正态分布近似概率分布函数.由MLE法可得其参数µ=2.175 0,σ=1.213 4.

另外,给出了不同阈值对应的PSD-LDA模型的参数估计(见表6).

3.3 财产保险欺诈损失纯保费估计

u=75时,把表6中相关参数代入式(3)，可得保险欺诈风险损失的纯保费为E(SN)=7 028万元.事实上,由于“欺诈暗数”的存在,实际的欺诈损失纯保费值肯定高于该数值.Caron和Dionne[26]研究证实“保险人能发现的欺诈比例仅为三分之一”.可见,欺诈提高了保险产品的价格.

3.4 财产保险欺诈损失度量及经济资本的测定

u=75时,根据PSD-LDA方法和蒙特卡洛模拟步骤得到估计结果(见表7).把表6中相关参数分别代入式(4)和式(5),可得POT极值法估计的结果(表7).表7还给出了损失分布法中运用单一对数正态分布和单一GPD分布拟合损失强度的估计结果.表8给出了阈值u=62,80时PSD-LDA模型的度量结果.

表6 两阶段损失序列参数估计(n=167)Table 6 Parameter estimation of PSD-LAD(n=167)

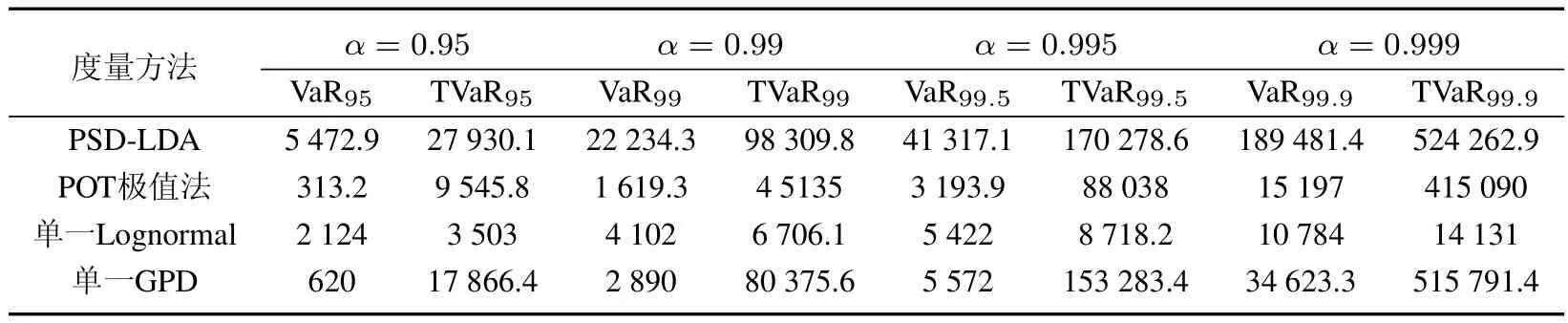
表7 不同度量方法下欺诈损失的VaR值与TVaR值(万元)Table 7 VaR value and TVaR value of fraud losses under different measurement methods

表8 贝叶斯估计下不同阈值的度量结果(万元)Table 8 Measurement results under different thresholds by Bayesian estimation

由表7可知:1)根据PSD-LDA方法的度量结果,给定置信水平99.5%,我国财产保险业在1年内欺诈风险最大损失值VaR为4.131 7亿元,损失超过该VaR值后的平均潜在损失为17.027 9亿元.给定置信水平99.9%,在1年内欺诈风险最大损失值为18.948 1亿元,损失超过18.948 1亿元后的平均潜在损失为52.426 3亿元;2)相同方法、同一置信水平下的TVaR值远大于VaR值,高置信水平(99.9%)下的TVaR值、VaR值明显高于低置信水平下(95%)下的TVaR值、VaR值,说明财产保险欺诈损失尾部风险很大;3)不同方法度量结果不同,比较而言,PSD-LDA方法最优.POT模型在置信水平较低时,相应的VaR、TVaR较低,如VaR95=313.2,TVaR95=9 545.8;当置信水平较高时,VaR,TVaR显著增高,如VaR99.9=15 197,TVaR99.9=415 090,表明POT模型只适用于度量尾部风险.另外,POT模型仅对少量超阈值数据拟合,造成大量的数据浪费,从而丢失许多有用的信息.单一对数正态分布法各置信水平下TVaR值、VaR值相差不大,在高置信水平下低估了欺诈风险损失,如TVaR99.9仅为14 131,与其他三种方法计算结果相差甚远.该法对拟合样本数据主体较好,但不能捕获欺诈风险厚尾特点,对尾部风险估计较低.单一GPD损失分布法,各置信水平下的TVaR值(如TVaR99.9=515 791.4)与PSD-LDA方法(如TVaR99.9=524 262.9)非常接近,不过该法估计的置信水平95%和99%的VaR值很低,如VaR95值仅为620,VaR99=2 890.该法对尾部估计较好,对样本数据的主体部分拟合效果较差.可见,在对财产保险欺诈风险损失的度量中,如果仅采用单一的传统损失分布法或单一的POT极值法,对损失分布的主体和尾部特征的捕捉会顾此失彼.PSD-LDA结合了对数正态分布和GPD分布的优点,并且是针对全部样本数据建模,同时考虑“低频高损”与“高频低损”风险,因而既能对损失数据主体有较好的拟合,又能很好地描述分布的厚尾特点,这可从表7中PSD-LDA方法度量的各置信水平下的TVaR和VaR值的结果得到反映.图9给出了表7中各种分布对原始数据经验分布的拟合情况,由图9可知,PSD-LDA方法对原始数据拟合最好.因此,采用PSD-LDA法对财产保险欺诈损失进行度量较其他方法更为合理精确.

另外,由表8可知,阈值选择不同对经济资本(TVaR99.9)的估计有一定影响.比如,阈值从62万元到75万元变化了21%,但欺诈风险经济资本变化了13.4%,阈值从75万元到80万元变化了6.7%,但欺诈风险经济资本变化了23.2%.因此,阈值的选择应当慎重.

采用置信水平为99.9%、时间为一年的TVaR值计提财产保险欺诈风险经济资本.假定财产保险公司对欺诈风险预期损失通过纯保费的方式在定价中已经体现,根据PSD-LDA方法,整个财产保险行业需要计提的欺诈风险经济资本EC=TVaR99.9−E(SN)=51.723 5亿元,能抵御千年一遇的巨额财产保险欺诈风险.2011年底,我国财产保险业总资产7 917.4亿元,因此需计提6.53‰的经济资本以抵御欺诈风险. 2004−2012年,财险年均保费收入2 871.941 9亿元,其中机动车保费收入1 820.34亿元,占63.4%,因此欺诈风险经济资本占年均保费收入的18‰,占机动车保费收入28.4‰.可见欺诈风险比较严重.

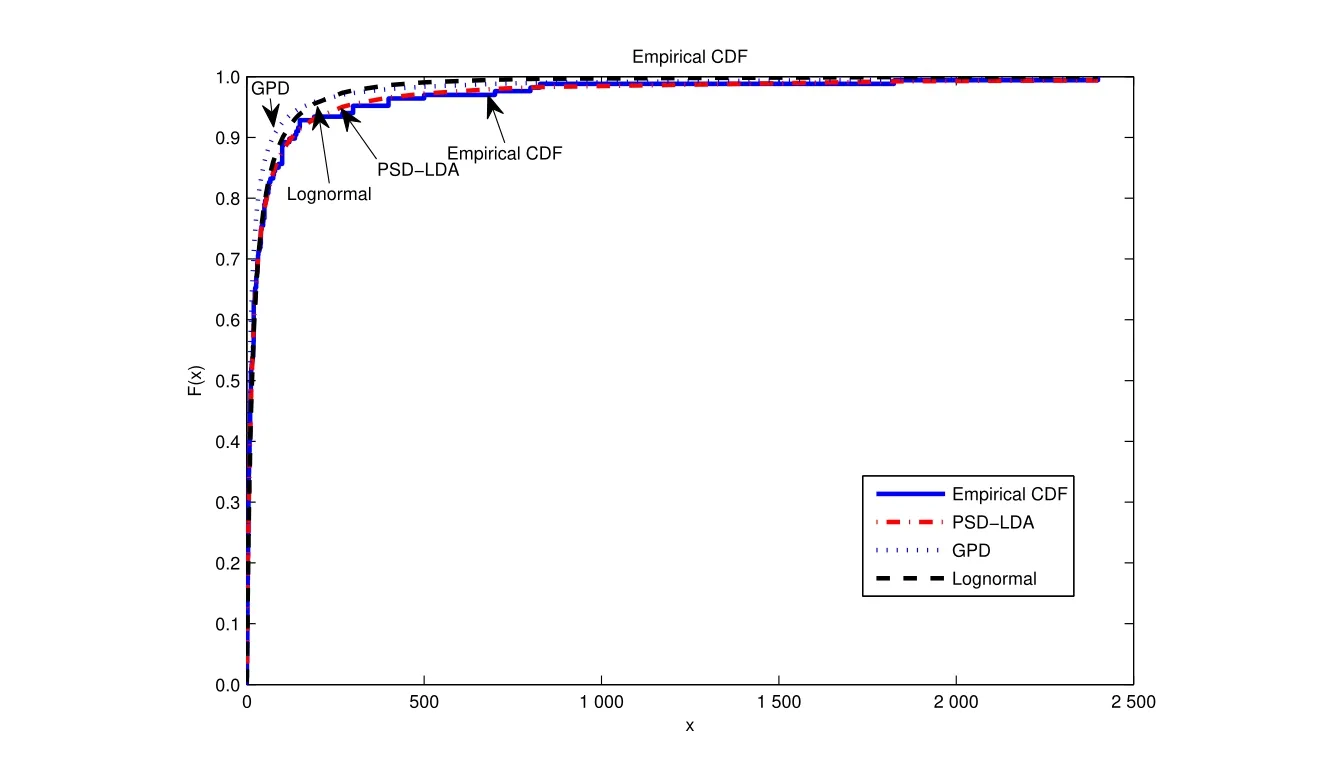
图9 不同度量方法对经验分布的拟合效果Fig.9 Different metrics ftting effect on the empirical distribution fgure

4 结束语

本文采用PSD-LDA方法，通过Monte Carlo模拟得到财产保险欺诈损失VaR和TVaR值,并测算了其经济资本和损失纯保费.研究结果表明:1)财产保险年欺诈纯保费为7 028万元,欺诈提高了保险产品价格;保险行业为应对欺诈风险,必须计提经济资本达52亿元,占总资产的6.53‰,占年均保费收入的18‰,严重影响了保险公司经营效率.因此,应加大对保险欺诈的防范与打击力度;2)财产保险欺诈风险损失具有严重的厚尾分布,尾部损失的风险很大,因此应重点防范尾部风险的发生;3)PSD-LDA方法克服了单一损失分布法或单独使用POT方法度量欺诈风险的缺陷,既能对损失主体有较好的拟合,又能对分布的“厚尾”特点给以很好的描述,因此采用这种方法度量欺诈风险比较合理.研究结果对于我国建立商业保险欺诈风险准备金制度、逐步建立以经济资本为核心的欺诈风险管理体系、欺诈风险监测预警机制以及完善保险产品定价机制具有重要的应用价值.

[1]Picard P.Economic analysis of insurance fraud[C]//Dionne G.Handbook of Insurance.New York:Springer,2013:315–316.

[2]中国保监会.关于加强反保险欺诈工作的指导意见[EB].http://www.circ.gov.cn/tabid/5171/InfoID/219312/frtid/5225/Default.aspx,2012-08-06/2013-05-08.

China Insurance Regulatory Commission.Guiding Opinions on Strengthening the Work of Anti-insurance Fraud[EB]. www.circ.gov.cn/tabid/5171/InfoID/219312/frtid/5225/Default.aspx,August 6,2012/May 8,2013.(in Chinese)

[3]Tripp M H,Bradley H L,Devitt R,et al.Quantifying operational risk in general insurance companies[J].British Actuarial Journal, 2004,10(5):919–1026.

[4]Dexter N,Ford C,Jakhria P,et al.Quantifying operational risk in life insurance companies[J].British Actuarial Journal,2007,13(2): 257–337.

[5]Paudel Y.Quantifying operational risk in insurance companies[J].Actuarial Sciences,2008,58(1):24–29.

[6]Lambrigger D D,Shevchenko P V,Wuthrich M V.Data combination under Basel II and Solvency II:Operational risk goes Bayesian[J].French Actuarial Bulletin,2008,8(16):4–13.

[7]Perez M J.Analyzing solvency with extreme value theory:An application to the Spanish motor liability insurance market[J].Journal of Innovar,2010,20(36):35–48.

[8]Bolance C,Ayuso M,Guillen M.A nonparametric approach to analyzing operational risk with an application to insurance fraud[J]. Journal of Operational Risk,2012,7(1):57–75.

[9]Morales R,Anibal J,Hurtado M.Estimation of operative risk for fraud in the car insurance industry[J].Global Journal of Business Research,2012,6(3):73–83.

[10]周孝华,董耀武,姜 婷.基于EVT-POT-SV-GED模型的极值风险度量研究[J].系统工程学报,2012,27(2):152–159.

Zhou Xiaohua,Dong Yaowu,Jiang Ting.Extreme risk measurement based on EVT-POT-SV-GED model[J].Journal of Systems Engineering,2012,27(2):152–159.(in Chinese)

[11]King J L.Operational Risk Measurement and Modeling[M].New York:Wiley,2001:87–113.

[12]Li Jianping,Feng Jichuang,Chen Jianmin.A piecewise-defned severity distribution-based loss distribution approach to estimate operational risk:Evidence from Chinese national commercial banks[J].International Journal of Information Technology and Decision Making,2009,8(4):727–747.

[13]王丽珍,李秀芳.基于偿付能力的最优再保险策略[J].系统工程学报,2012,27(1)：44–51.

Wang Lizhen,Li Xiufang.The optimal reinsurance strategy based on maximal possible claims principle[J].Journal of Systems Engineering,2012,27(1):44–51.(in Chinese)

[14]Basak S,Shapiro A.Value-at-Risk-based risk management:Optimal policies and asset prices[J].Review of Financial Studies,2001, 14(2):371–405.

[15]刘喜华,金加林.保险欺诈博弈与基于最优博弈策略的保险契约[J].系统工程理论与实践,2004,24(2):19–24.

LiuXihua,JinJialin.Insurancefraudgameandinsurancecontractbasedonoptimalgamestrategies[J].SystemsEngineering:Theory &Practice,2004,24(2):19–24.(in Chinese)

[16]边文霞.保险欺诈博弈研究[M].北京:首都经济贸易大学出版社,2006.

Bian Wenxia.Insurance Fraud Game Research[M].Beijing:Capital University of Economics and Business Press,2006.(in Chinese)

[17]叶明华.基于BP神经网络的保险欺诈识别研究:以中国机动车保险索赔为例[J].保险研究,2011(3):79–86.

Ye Minghua.Insurance fraud recognition based on BP Neural Networks:A case study in Chinese motor insurance claims[J].Insurance Studies,2011(3):79–86.(in Chinese)

[18]陈 亮.改进的贝叶斯网络模型在保险欺诈挖掘中的应用[J].河南城建学院学报,2012(1):50–53.

Chen Liang.Application of improved Bayesian network to discover insurance fraud[J].Journal of Henan University of Urban Construction,2012(1):50–53.(in Chinese)

[19]ValleD,Giudici P.A Bayesian approach to estimate themarginalloss distributions in operationalrisk management[J].Computational Statistics&Data Analysis,2008,52(10):3107–3127.

[20]Leadbetter M R.On a basis for‘Peaks over Threshold’modeling[J].Statistics&Probability Leters,1991,12(4):357–362.

[21]Bermudez P Z,Turkman M A.Bayesian approach to parameter estimation of the generalized pareto distribution[J].Test:An Offcial Journal of the Spanish Society of Statistics and Operations Research,2003,12(1):259–277.

[22]王宗润,汪武超,陈晓红.基于BS抽样与分阶段定义损失强度操作风险度量[J].管理科学学报,2012(12):58–69.

Wang Zongrun,Wang Wuchao,Chen Xiaohong.Application of LDA based on Bootstrap sampling and piecewise defned severity distribution in operational risk measuremen[J].Journal of Management Sciences in China,2012(12):58–69.(in Chinese)

[23]McNeil A J.Estimating the tails of loss severity distributions using extreme value theory[J].ASTIN Bulletin,1997,27(1):117–137.

[24]Bottolo L,Consonni G,Dellaportas P.A Bayesian analysis of extreme values by mixture modeling[J].Extremes,2003,6(1):25–48.

[25]DuMouchel W H.Estimating the stable indexαin order to measure tail thickness:A critique[J].Annals of Statist,1983,11(4): 1019–1031.

[26]Caron L,Dionne G.Insurance fraud estimation:More evidence from Quebec automobile insurance industry[C]//Laberge C,Dionne G.Automobile Insurance:Road Safety,New Drivers,Risks,Insurance Fraud and Regulation.Massachusetts:Kluwer,1999:175–182.

Empirical study of measuring property insurance fraud loss in China

Lin Yuan1,2,Li Lianyou1
(1.School of Finance and Statistics,Hunan University,Changsha 410082,China; 2.Huaihua University,Huaihua 418008,China)

Based on Bayesian Markov chain Monte Carlo(MCMC)method to estimate parameters,this paper proposes a loss distribution approach based on piecewise-defned severity distribution(PSD-LDA)to calculate the potential losses Tail VaR of property insurance fraud risk,its economic capital,and net premiums.We compare the results derived with other methods such as peaks over threshold(POT)method and single loss distribution approach.Empirical results show that property insurance fraud losses have fat tail risks,and the PSD-LDA model is more rational in measuring its fraud risk,which can provide a theoretical basis for the pricing of insurance products and the decisions of insurance fraud risk management.

insurance fraud;generalized Pareto distribution;Gibbs sampling;economical capital

G22;G32

A

1000−5781(2015)04−0509−10

10.13383/j.cnki.jse.2015.04.008

2013−11−22;

2014−06−16.

国家社会科学基金资助项目(12BGL091);教育部人文社科基金一般资助项目(12YJAZH069);湖南省软科学研究计划资助项目(2013ZK3049).

林 源(1968—),男,湖南沅陵人,博士,副教授,研究方向:风险管理与保险,E-mail:linyuan0011@126.com;

李连友(1965—),男,湖南安乡人,博士,教授,研究方向:风险管理与保险,E-mail:pkuyoully@263.net.