离散累积前景理论下的投资组合选择
2015-10-26林祥亮马成虎范龙振
林祥亮,马成虎,2,范龙振
(1.复旦大学管理学院,上海200433; 2.复旦金融研究中心,上海200433)
离散累积前景理论下的投资组合选择
林祥亮1,马成虎1,2,范龙振1
(1.复旦大学管理学院,上海200433; 2.复旦金融研究中心,上海200433)
提出了离散情形下的累积前景理论(CPT)模型,讨论了CPT价值函数的性质(包括连续可微性、一阶随机占优性、凹凸性等),给出了投资组合适定的一般条件及两种特殊情形下最优投资组合的解析解.研究发现,存在一个与投资者效用密切相关的临界点.当超过这个临界点时,投资于风险资产的额度为有限的;反之,投资于风险资产的额度是无限的.最后提供了连续分布情形下最优解依离散分布最优解收敛的定理.
离散分布;累积前景理论;投资组合;收敛性;适定性
1 引 言
实验经济学研究表明,人们在面临随机或不确定性决策时的行为模式可能不满足期望效用理论[1,2].经济学家试图改进期望效用理论以期获得更符合实际的结论.Kahneman等[3]提出的前景理论和Tversky等[4]提出的累积前景理论(简称CPT)是这方面工作的重要成就,此种理论主要通过修正最大主观期望效用理论发展而来.
累积前景理论的基本要点有:1)效用函数的正负依赖于参考点的选择,大于参考点的财富的效用函数是凹函数,小于参考点的财富的效用函数是凸函数,该行为特征称之为“参照依赖”.2)在参考点处,效用函数的右导数小于左导数,该类行为特征称之为“失望规避”[5]或者“损失规避”[6−8].3)权重函数是逆S型概率扭曲函数[3].也就是说,很多事件发生的概率很小,但人们总是夸大它的影响;同时,很多事情发生的概率很大,但人们总是贬低它的影响,该行为特征称之为“迷恋小概率事件”[9−17].
最近,很多学者对累积前景理论做了深入的探讨.Barberis等[18]证明了在风险资产收益率满足正态分布并且投资者满足同质偏好的条件下,存在CPT假定下的均衡CAPM.Bernard等[19]研究了满足幂效用函数的价值函数和Tversky等[4]中的权重函数的特殊情形的CPT模型,得到了模型的解析解以及解的各种性质. He等[20]提出了连续情形下的CPT模型,提出了模型的适定性和不定性的定义并解决了最优解的存在性问题.Ingersoll[21]回答了一些资产定价领域更为基本的问题,包括对CPT投资者来说何种条件下,市场组合满足市场有效性、二基金分离定理以及均值方差分析.国内文献中,邹高峰等[22]在中国资本市场环境下建立了资本资产定价模型(PTCAPM),并表明其所构建的PTCAPM模型比传统的CAPM具有更强的解释能力.
在CPT的应用方面,Hens[23]等表明前景理论不能解释处置效应.Pfffelmann[24]表明对概率权重函数做限制性的假定,CPT可以解释圣彼得堡悖论.Jin[25]等在CPT下量化了“贪心”的概念,发现其与杠杆和潜在损失之间的关系.解释了即使存在严重损失的风险,“贪心”行为投资者仍然进行投资.
本文在投资者满足参照依赖、损失规避以及迷恋小概率事件的假定下提出了离散情形下的CPT模型,给出了投资者的CPT价值函数的定义,讨论了CPT价值函数的各种性质,包括它的连续可微性、一阶随机占优性.本文发现,虽然超额收益率的分布是离散的,但投资者的价值函数是连续可微的.与之前很多学者的结论类似[4,20],本文的价值函数满足一阶随机占优性.本文给出了CPT模型下投资组合适定性的定义,证明了满足适定解存在的条件,并指出此条件的经济意义.另外,本文给出了两种特殊情况下的解析解.最后本文证明了CPT模型解的收敛性,也就是离散情形下CPT模型的最优解收敛到连续情形下CPT模型的最优解.对于超额收益率为连续分布的情形,在某些情形下利用连续CPT模型得到解析解较为困难,解析解的形式也很复杂[20],而利用离散CPT模型得到解析解较为容易(本文定理4),此种情况下可采用将分布函数离散化的方式进行处理,这为处理复杂投资组合问题提供了捷径,这也为实证研究提供了便利.另外,本文为探讨期望效用投资者和CPT投资者的投资行为的差异奠定了基础,并为下一步研究由CPT投资者构成的市场中一般分布下的均衡定价提供了准备条件.
2 模 型
考虑一个仅有一种风险资产和一种无风险资产的市场.设R为风险资产的净收益率,r为常数,表示无风险利率.R−r称为超额收益率,假设其分布函数为离散的,即
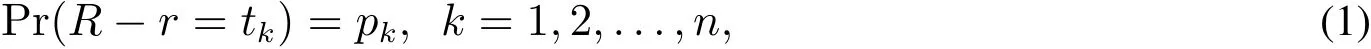
其中t1>t2>···>tm>0>tm+1>···>tn,m为超额收益率取值为正负的分界点.
考虑一个具有CPT偏好投资者的投资选择问题.投资者偏好包含如下三个组成部分:
1)投资者的参考点为B.当投资者的收益大于B时,投资给投资者带来正效用;当投资者的收益小于B时,投资给投资者带来负效用.
2)u+和u−分别代表定义于以B为参考点的财富区间上的正、负效用函数.
假定1 超额收益率满足0
假定2 u±:R+→R+为单增二次连续可微的凹函数,且u±(0)=0,u±(+∞)=+∞.
假定4 证券资产可以无限细分,风险资产不存在卖空限制.
设投资者的初始财富为W0,该投资者投资于风险资产的财富为θ,其余财富投资于无风险资产,则投资者的最终财富为

其中x0=(1+r)W0−B表示无风险收益与参考点的偏差.
令xk=x0+B+θtk,k=1,2,...,n.当θ>0时,得到x1>x2>···>xm>xm+1>···>xn.此时,离散形式的CPT价值函数为

其中m(θ)为满足xm(θ)>B>xm(θ)+1的正整数(当x0>0时,如果不存在m(θ)使得此式成立,则令m(θ)= n;当x0<0时,如果不存在m(θ)使得此式成立,则令m(θ)=0),w+(pk)(Pr(R−r>tk+1))−(Pr(R−r>tk)),w−(pk)(Pr(R−r 当θ<0时,有x1 其中m(θ)为满足xm(θ)+1>B>xm(θ)的整数(当x0>0时,如果不存在m(θ)使得此式成立,则令m(θ)=0;当x0<0时,如果不存在m(θ)使得此式成立,则令m(θ)=n),w+(pk)Pr(R−r>tk−1))−(Pr(R−r>tk)),w−(pk)(Pr(R−r 定义 注意 1)当x0=0时,对式(2)和式(3)中的m(θ),恒有m(θ)=m. 2)θ<0表示投资者卖空风险资产的情况,卖空的数量为|θ|,为简单计,本文没有假定投资者采用保证金制度卖空风险资产. 3)由式(4)容易得到,当x0>0时,U(0)>0;当x0<0时,U(0)<0,并且价值函数与概率权重函数无关,说明任何投资者只要其参考点相同,在不投资于风险资产时的价值函数是相同的. 引理1 1)当x0>0且θ>0时,m(θ)单减;当x0>0且θ<0时,m(θ)单减;当x0<0且θ>0时,m(θ)单增;当x0<0且θ<0时,m(θ)单增;当x0=0时,m(θ)=m. 2)当θ→∞时,m(θ)→m. 如果投资者的参考点低于无风险收益,那么当该投资者买入更多风险资产时,收益大于参考点的可能性降低;相反,如果投资者的参考点高于无风险收益,那么当该投资者买入更多风险资产时,收益大于参考点的可能性升高.如果投资者的参考点低于无风险收益,那么当该投资者卖空更多风险资产时,收益大于参考点的可能性升高;相反,如果投资者的参考点高于无风险收益,那么当该投资者卖空更多风险资产时,收益大于参考点的可能性降低.如果投资者的参考点为无风险收益,那么不论是买入资产还是卖空资产,收益大于参考点的可能性不变,只与风险资产的超额收益的分布有关.总而言之,投资者的收益与参考点之间的孰大孰小的概率不仅与参考点与无风险收益的大小有关,还与投资者买入还是卖空资产有关. 当投资者买入大量的风险资产或者卖空大量的风险资产时,投资者的收益大于参考点的可能性趋于不变,不变量只与风险资产的超额收益的分布有关. 命题1 以上定义的U(θ),∀θ∈R′,在x0固定时是连续可微的,并且在θ=0时,有 命题1说明给定参考点与无风险收益之间的差额,投资者的价值函数是连续变化的,不会出现跳跃,这与现实是相符的.但是如果投资者的参考点连续变化时,投资者的价值函数却在无风险收益处有跳跃,这从式(4)中可以容易得出,这说明无风险收益是投资者的重要的参考标准. 当x0>0时,记(R−r)=表示投资者对风险资产的超额收益率的主观期望.由于此期望必然大于零(否则投资者不会投资于此种资产),所以U′(0)>0.同理,当x0<0时,记(R−仍然表示投资者对风险资产的主观超额收益率的期望,因此U′(0)>0.这就是说,只要x00,投资于少量风险资产会增加投资者的价值.当x0=0时,记E+(R−r)(−tk)w−(pk)分别表示投资者对风险资产的超额收益率的正主观期望和负主观期望. 命题2 由式(2)–式(3)定义的CPT价值函数满足一阶随机占优性. 一阶随机占优性质成立表明投资者持有占优资产预期效用总是更高的,因此,投资者总会持有占优资产.一般情况下,由式(2)–式(3)定义的CPT价值函数不满足二阶随机占优单调性,这在Bernard等[19]一文中有反例. 投资者的最优投资组合问题是 定义1 如果极值可达,且在最优解处投资于风险资产的资金是有限的(即θ有限值),则称问题(P)为适定的;反之,则称问题(P)为不定的. 令 有如下结论. 定理1 当k=∞时,问题(P)为适定的;当k=0时,问题(P)为不定的. 直观上讲,从式(5)的定义中可以看出,k=∞说明投资于风险资产或者卖空风险资产的数额足够大时,对投资者来说负的效用远大于正的效用.因此投资者会选择投资有限数额于风险资产中.换一种说法, k=∞表明投资者非常规避看跌风险,因此不会在风险资产上投入太多金额,即使风险资产的平均收益很大.相反,当k=0时,投资于风险资产或者卖空风险资产的数额足够大时,负的效用远远小于正的效用,投资者会尽量投资更多数额的风险资产. 引理2 令 则有 且若0 令k0=max{a1/b1,a2/b2},有如下结论. 定理2 若0 直观地说,对投资者来说,存在一个与投资者效用的主观期望密切相关的临界点.当超过这个临界点时,投资于风险资产的额度为有限的;反之,投资于风险资产的额度是无限的.由引理2及k0的定义,有 同理,有 因此,k>k0等价于 k 这样,可以如下理解定理:当投资于风险资产的数额足够大或者卖空风险资产的数额足够大时,若投资者获得的正条件期望效用大于负条件期望效用,则投资者会买入或者卖空无限数额的风险资产;反之,投资者会投资有限数额的资金于风险资产. 这样,验证了对于部分效用函数,价值函数为非凸非凹函数,对求解优化问题在技术上产生困难. 由于问题(P)的复杂性,本文没有得到一般情形下它的解析解.以下本文就两种特殊情形推出问题(P)的解析解. 由于幂效用函数在经济和金融上都有广泛的应用,本文首先研究它的解析解.以下定理表明幂效用函数情形下最优解不仅与效用函数的相对系数(γ)有关,也与效用函数的相对风险规避系数有关. 定理3 如果效用函数的形式为u+(x)=xα,u−(x)=γxβ,γ>0,0<α,β<1,那么, 1)当α<β时或者当α=β并且γ>k0时,问题(P)是适定的;当α>β时或者当α=β并且γ 以下结果均假定x0=0. 其中a1,a2,b1,b2定义见引理2. 3)当α=β并且γ>k0时,问题(P)的最优解为θ∗=0. 4)当α=β并且γ=k0=a1/b1时,任意θ>0均为最优解. 5)当α=β并且γ=k0=a2/b2时,任意θ60均为最优解. 线性效用函数由于其性质简单并可作为很多效用函数的基准受到不少经济学家的关注[7],其本质上是投资者对参考点处的凹凸性不是很看重,也就是说,如果投资者趋于风险中性,可近似采用线性效用函数. 定理4 假设u+(x)=x,u−(x)=γx,则有 4)假设问题(P)是适定的,记 其中K=m,m+1,...,n.若x0>0,则价值函数的最大值为 本文进而探讨连续分布作为离散分布的极限情形下的最优投资组合选择问题.关于连续分布下CPT投资者的最优选择问题,在He等[20]的文章中有较为深入的讨论.由于任意给定的连续分布函数都可由有限支撑的离散分布逼近,自然要问:这两种情况下得到的结论是否一致?也就是说,本文讨论的离散情形的解是否收敛到连续情形的解? 令FT(t)为对应于超额收益率的连续分布函数,且满足He等[20]的文章中假定3的条件.此时有: 当θ>0时, 当θ<0时, 记Θ={θ∈R′|U(θ)在θ达到最大值},Θ(n)={θ∈R′|U(n)(θ)在θ达到最大值}分别为对应于连续分布和离散分布情形下最优解的解集.记θ∗,arg minθΘ;,arg minθΘ(n). 定理5 如果问题(P)是适定的,则当n→∞时,对任意有界的θ有U(n)(θ)→U(θ)并且→θ∗. 这个从现实中来看也是很有意义的,定理说明,如果超额风险的分布比较复杂,投资者可以采用将分布函数离散化的方法得到离散情形下的在风险资产上的最优投资额,以此来逼近原始连续分布问题的解.由于离散情形的最优投资额收敛于连续情形的最优投资额,这个近似是合理的,并且所取的离散化分布函数越接近,得到的结果近似程度越好. 本文提出了离散情形下的累积前景理论(CPT)模型,探讨了CPT偏好投资者的最优投资选择问题,并提供了离散分布情形下CPT投资者所对应的问题解的收敛性定理.研究发现,存在一个与投资者效用密切相关的临界点.当超过这个临界点时,投资于风险资产的额度为有限的;反之,投资于风险资产的额度是无限的.本文结论在多个风险证券投资且投资收益服从无限支撑离散分布的情况下也成立.后续研究主要包括多期CPT偏好特征的推广及动态投资选择问题,做空保证金对投资行为的影响问题以及参考点内生性对定对投资行为的影响问题. 感谢严加安院士、汤善健教授对文章进一步修改所提的意见以及王甜甜博士在本文写作过程中对作者的帮助. [1]Allais M.Le comportement de l′homme rationnel devant le risque:Critique des postulates et axioms de l′ecole Americans[J]. Econometrica,1953,21(4):503–546. [2]Ellsberg D.Risk,ambiguity,and the savage axioms[J].Quarterly Journal of Economics,1961,75(4):643–669. [3]Kahneman D,Tversky A.Prospect theory:An analysis of decision under risk[J].Econometrica,1979,47(2):263–291. [4]Tversky A,Kahneman D.Advances in prospect theory:Cumulative representation of uncertainty[J].Journal of Risk and Uncertainty, 1992,5(4):297–323. [5]Gul F.A theory of disappointment aversion[J].Econometrica,1991,59(3):667–686. [6]Tversky A,Kahneman D.Loss aversion in riskless choice:A reference-dependent model[J].Quarterly Journal of Economics,1991, 106(4):1039–1061. [7]Benartzi S,Thaler R H.Myopic loss aversion and the equity premium puzzle[J].Quarterly Journal of Economics,1995,110(1): 73–92. [8]Thaler R,Tversky A,Kahneman D,et al.The effect of myopia and loss aversion on risk taking:An experimental test[J].Quarterly Journal of Economics,1997,112(2):647–661. [9]Quiggin J.A theory of anticipated utility[J].Journal of Economic Behavior&Organization,1982,3(4):323–343. [10]Quiggin J.Comparative statics for rank-dependent expected utility theory[J].Journal of Risk and Uncertainty,1991,4(4):339–350. [11]Yaari M.The dual theory of choice under risk[J].Econometrica,1987,55(1):95–115. [12]Luce R D.Rank dependent,subjective expected utility representations[J].Journal of Risk and Uncertainty,1988,1(3):305–332. [13]Segal U.Non-expected utility risk premiums:The cases of probability ambiguity and outcome uncertainty[J].Journal of Risk and Uncertainty,1988,1(3):333–347. [14]Gonzalez R,Wu G.On the shape of the probability weighting function[J].Cognitive Psychology,1999,38(1):129–166. [15]Kliger D,Levy O.Theories of choice under risk:Insights from fnancial markets[J].Journal of Economic Behavior&Organization, 2009,71(2):330–346. [16]Polkovnichenko V,Zhao F.Probability weighting functions implied in options prices[J].Journal of Financial Economics,2013, 107(3):580–609. [17]Bernard C,He X D,Yan J A,et al.Optimal insurance design under rank-dependent expected utility[J].Mathematical Finance,doi: 10.1111/maf.12027. [18]Barberis N,Huang M.Stocks as lotteries:The implications of probability weighting for security prices[J].American Economic Review,2008,98(5):2066–2100. [19]Bernard C,Ghossoub M.Static portfolio choice under cumulative prospect theory[J].Mathematical Financial Economics,2010, 2(4):277–306. [20]He X D,Zhou X Y.Portfolio choice under cumulative prospect theory:An analytical treatment[J].Management Science,2011, 57(2):315–331. [21]Ingersoll J E.Cumulative prospect theory and the representative investor[R].Working Paper,2011.http://www-test.stern.nyu.edu /cons/groups/content/documents/webasset/con 032490.pdf. [22]邹高峰,张 维,张海峰,等.中国市场条件下的前景理论资本资产定价模型[J].系统工程学报,2013,28(3):355–361. Zou Gaofeng,Zhang Wei,Zhang Haifeng,et al.Prospect theory-based capital asset pricing model based on China security market[J]. Journal of Systems Engineering,2013,28(3):355–361.(in Chinese) [23]Hens T,Vlcek M.Does prospect theory explain the disposition effect[J].Journal of Behavioral Finance,2011,12(3):141–157. [24]Pfffelmann M.Solving the St.Petersburg Paradox in cumulative prospect theory:The right amount of probability weighting[J]. Theory and Decision,2011,71(3):325–341. [25]Jin H Q,Zhou X Y.Greed,leverage,and potential losses:A prospect theory perspective[J].Mathematical Finance,2013,23(1): 122–142. [26]Patrick B.Probability and Measures[M].2nd ed.New Jersey:John Wiley&Sons,1986:390. 附录 定理证明 引理1的证明 1)下面仅证x0>0并且θ>0的情况,其余情况类似可证.当x0=0时,结论显然. 当x0>0并且θ>0时,由m(θ)的定义,知道θtm(θ)+x0>0,θtm(θ)+1+x0<0,故有tm(θ)>−x0/θ>tm(θ)+1,所以当θ增加时,tm(θ)也增加,所以m(θ)减少;同理,当θ减少时,m(θ)增加.所以m(θ)单调递减. 2)由于m(θ)单调有界,所以必然有极限.设当θ→∞时,m(θ)→m′,则由(1)的证明易知tm′>0>tm′+1,再由m的定义得到m′=m. 证毕. 命题1的证明 1)连续性.下面仅证x0>0并且θ>0时的情况,其余情况类似.当x0=0时,由引理1,m(θ)=m,再由u±(x)的连续性假定,易知U(θ)连续. 当x0>0并且θ>0时,记Θ∗={θ|m(θ)在θ点产生跳跃},分如下两种情况讨论. (i)若θ/∈Θ∗,则在θ附近m(θ)为常数,由u±(x)的连续性假定,易知U(θ)是连续的. (ii)若θ∈Θ∗,即θtm(θ)+x0=0,则由于m(θ)为单调递减函数,因此m(θ)为左连续的.当θ′<θ且θ′在θ附近时, m(θ′)=m(θ).这时,显然有U(θ)是连续的.当θ′>θ时,m(θ′)=m(θ)−1.此时, 易知,当θ′→ θ时,I1→ 0并且I3→ 0.由于θ∈Θ∗,所以I2=0.当θ′→ θ时,I4→ u−(θtm(θ)+x0)w−(pm(θ))= u−(0)w−(pm(θ))=0.因此,综上所述,当θ′→θ时,U(θ′)−U(θ)→0. 最后,鉴于U(0)为自行定义,证明U(θ)在0处的连续性是很有必要的.由于x0>0,所以当θ足够小时,θtk+x0>0对任意k恒成立,而由m(θ)的定义,m(θ)是满足θtk+x0>0成立的最大的值,因此m(θ)=n.显然,U(θ)在0处连续. 2)可微性.本文也仅证当x0>0并且θ>0时的情况,其余情况与之类似可证.此时,分如下两种情况讨论. (i)若θ/∈Θ∗,则在θ附近m(θ)为常数,由u±(x)的可微性假定,易知U(θ)是可微的. (ii)若θ∈Θ∗,当θ′<θ且θ′在θ附近时,可微性证明与连续性证明类似.当θ′>θ时,利用连续性的证明结果,有 由u±(x)的可微性以及θtm(θ)+x0=0的假定,易知 由以上四式得到U(θ)满足可微性. 对于U(θ)在0点的可微性以及U′(0)的值,由连续性部分的证明可知,当x0>0并且θ足够小时,可以证得m(θ)=n.因此,U(θ)在0点的可微性以及U′(0)的值是显然的. 证毕. 命题2的证明 假设有两个风险收益变量,分别为R1和R2,则超额收益率为R1−r和R2−r.记R1−r和R2−r的分布函数分别为F1(t)和F2(t).再假定R1−r一阶随机占优于R2−r,即F1(t)6F2(t),∀t∈(−∞,+∞).这样当θ>0时,式(2)规定的CPT价值函数为 因此,两个风险收益变量的CPT价值函数之差为 其中 由随机占优性的假定,上式两项均大于或等于零,因此K1>0.同理可得,K2>0.所以U1(θ)−U2(θ)>0.这样就证明了式(2)规定的CPT价值函数满足一阶随机占优条件.当θ<0时,证明类似. 证毕. 定理1的证明 1)当k=∞时,由He等[20]中定理1的证明得到:对于任意固定的x1,x2,以及t>0,均有 当θ>0时, 把价值函数写成如下形式 引理2的证明 下面仅证当x0>0并且θ>0的情况,其余类似.由引理1,当x0>0时,m(θ)>m.所以 若k有限,则 定理2的证明 下面仅证θ>0时的情况,θ<0时类似可证. 由引理2,当θ→+∞时,上式中花括号内的部分的极限为 命题3的证明下面仅证若U(+∞)=−∞和U′(+∞)=0同时成立,则U(θ)为非凹函数,其余类似. 仿照命题1的证明可得到,U(θ)的二阶导数在x0固定时是连续可微的.设U(θ)为凹函数,则U′′(θ)60,所以U′(θ)单调递减.再由U′(+∞)=0,得到U′(θ)>0,所以U(θ)单调递增.而U(+∞)=−∞,所以U(θ)=−∞,这是不可能的(因为由式(4),U(0)是有界的),因此U(θ)为非凹函数. 证毕. 定理3的证明 1)的证明由定理2得到. 2)因为x0=0,所以m(θ)=m.当θ>0时,令 得式(8)成立.经计算得 3)当θ>0时,U(θ)=θαb1(a1/b1−γ)<0,因此,当且仅当θ=0时,U(θ)达到最优解.当θ<0时,证明类似可得.因此,当且仅当θ=0时,U(θ)达到最优解. 4)当α=β并且γ=k0=a1/b1时,由U(θ)=θαb1(a1/b1−γ)=0易得任意θ>0均为最优解. 5)证明与4)类似.证毕. 定理4的证明 下面仅证θ>0时的情况,θ<0的情况类似可证.当θ>0时,由引理1,可以取θ足够大,使得m(θ)=m.此时 4)的证明仅需对x0>0并且θ>0时的情况进行论证.此时 同理,当θ<0时,价值函数的最大值为 由以上两式便可得到问题的结论.证毕. 定理5的证明 先证明第一部分.下面仅证θ>0时的情况,θ<0时的情况类似.由w+和w−的性质,以及(t)弱收敛到FT(t),得到w+(1−(t))→w+(1−FT(t)),以及w−((t))→w−(FT(t)).对任意有界的θ,u±有界,由基本定理[26]得到U(n)(θ)→U(θ). 第二部分的证明利用反证法.仅证θ∗>0的情况,其余类似.由于问题(P)是适定的,因此,θ∗取有界值的时候U(θ)达到最大值;取有界值的时候U(n)(θ)达到最大值.假定θ∗,则由维尔斯特拉斯定理,存在序列{},使得当j→+∞时,→θ∗.由U(·)的连续性,U(n,j)()→U()→U(.又因为当j→+∞时,U(n,j)()=maxU(n,j)(θ)→maxU(θ)=U(θ∗),所以U()=U(θ∗).由于θ∗为U(θ)取到最大值的情况下的最小值,所以>θ∗.所以对于δ=(−θ∗)/3,存在足够大J,使得当j>J时,>θ∗+2δ. 记{αn}为一列数,满足αn→θ∗.对于任意ϵ>0,存在非常大的数A,使得如下式子成立,即 因此,当n足够大时,有 下证当n足够大时,M1<4ϵ. Portfolios choices under cumulative prospect theory in the case of discrete distribution Lin Xiangliang1,Ma Chenghu1,2,Fan Longzhen1 The paper presents a cumulative prospect theory(CPT)model under discrete distributions.Some topological properties of the CPT value function,including differentiability,stochastic dominance and convexity,are discussed.General conditions for the well-pose of the portfolio choice problem with CPT value function are provided,in addition to analytical solutions obtained under two different sets of parametric model specifcations.The conclusion is that there is a critical point associated with the investor’s utility.When it exceeds this critical point,the amount invested in risky assets is limited;conversely,the amount is unlimited. As a separate contribution,this paper provides a convergence theorem for the CPT model under continuum distribution as a limit to the discrete counterparts. discrete distribution;prospect theory;portfolio;convergence;well-pose F830 A 1000−5781(2015)04−0494−15 10.13383/j.cnki.jse.2015.04.007 2013−06−16; 2014−05−09. 国家自然科学基金资助项目(71271058);复旦金融研究中心政策咨询团队资助项目(EZH43011021020). 林祥亮(1985—),男,江苏连云港人,博士生,研究方向:资产定价理论,Email:11110690009@fudan.edu.cn; 马成虎(1962—),男,山东威海人,博士,教授,博士生导师,研究方向:资产定价理论,Email:machenghu@fudan.edu.cn; 范龙振(1965—),男,河南虞城人,博士,教授,博士生导师,研究方向:资产定价理论,Email:lzfan@fudan.edu.cn.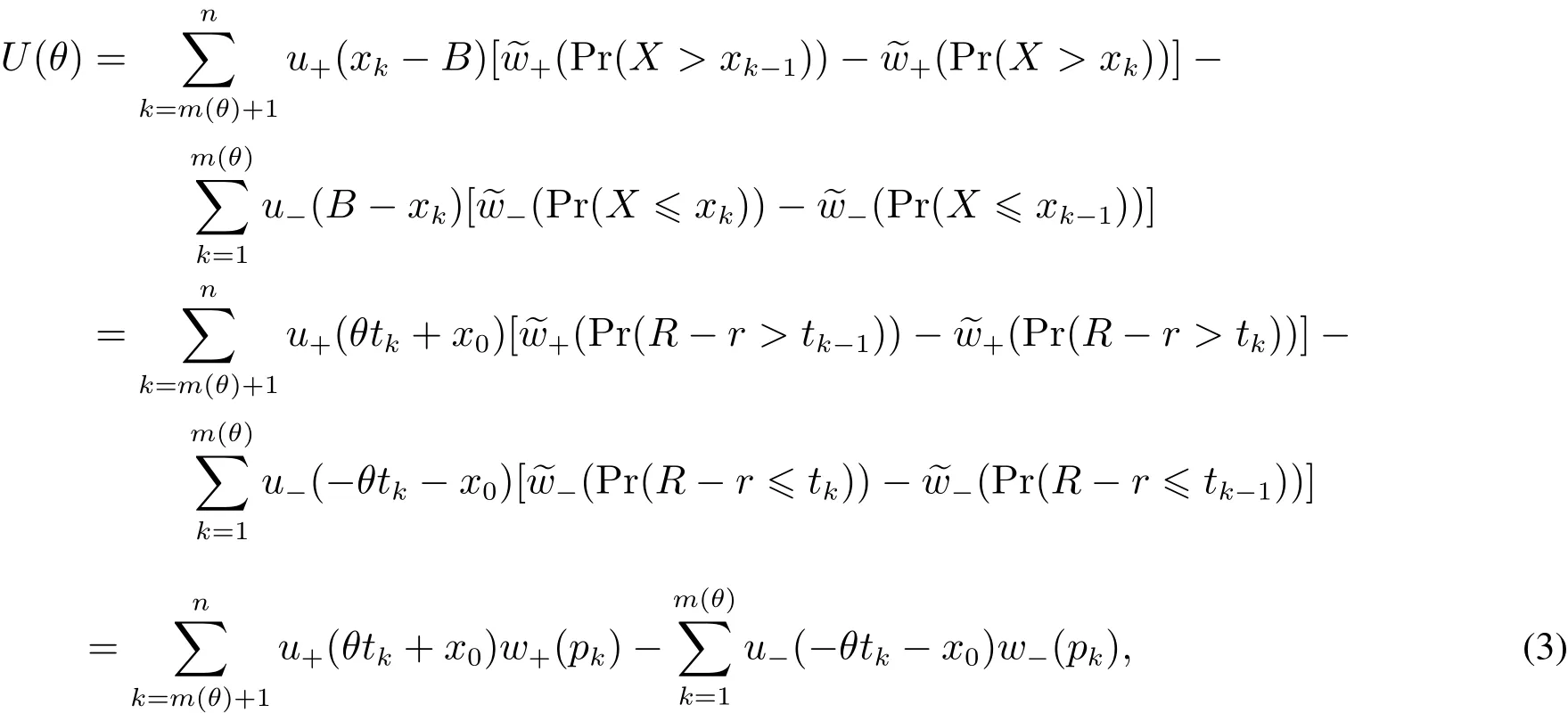
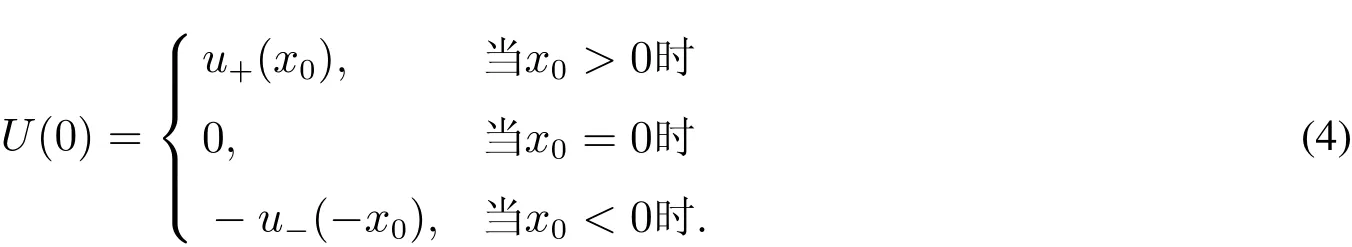
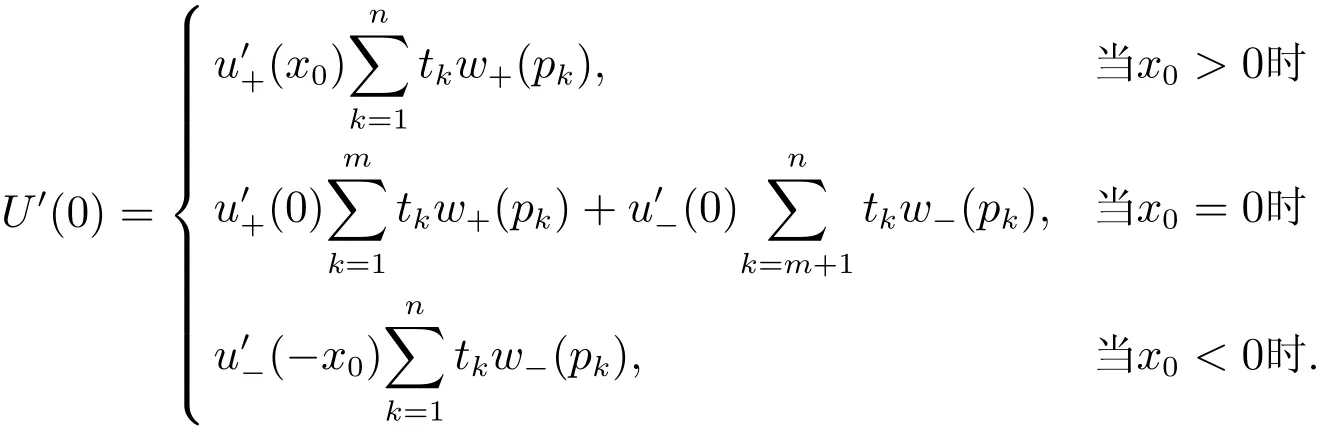
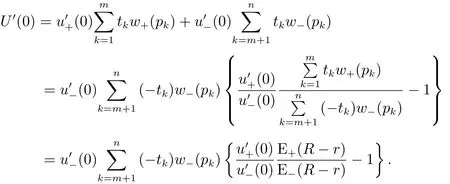
3 适定性与不定性


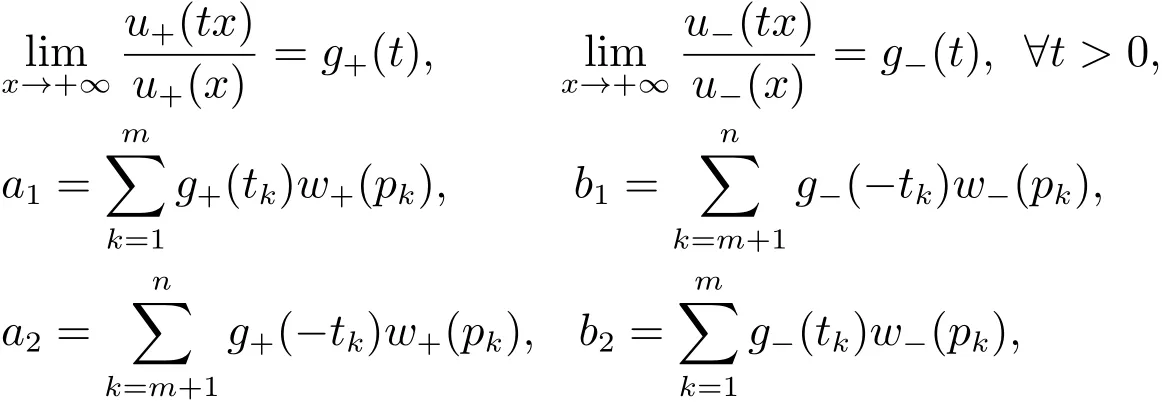
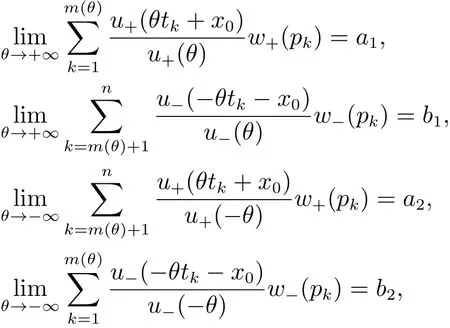



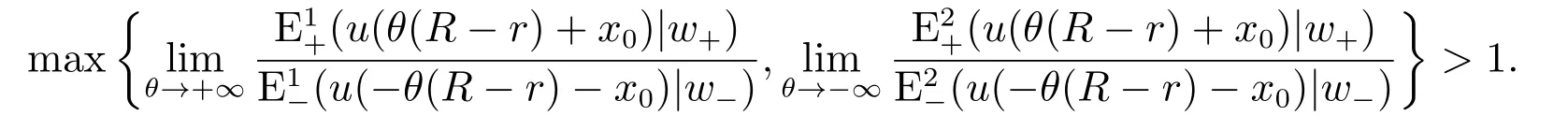
4 两种特殊情况的解析解
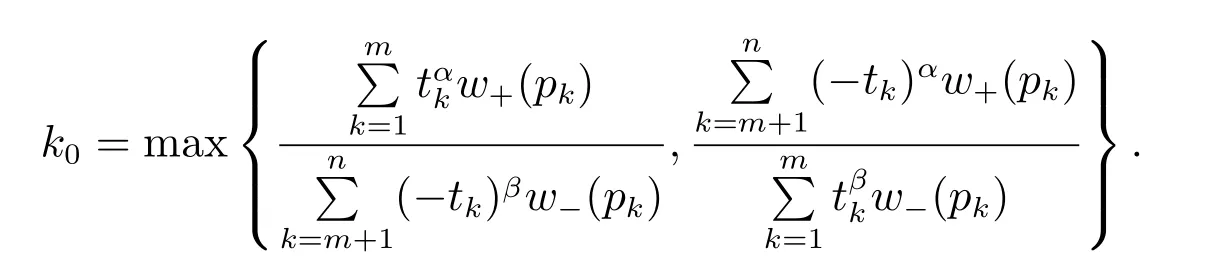


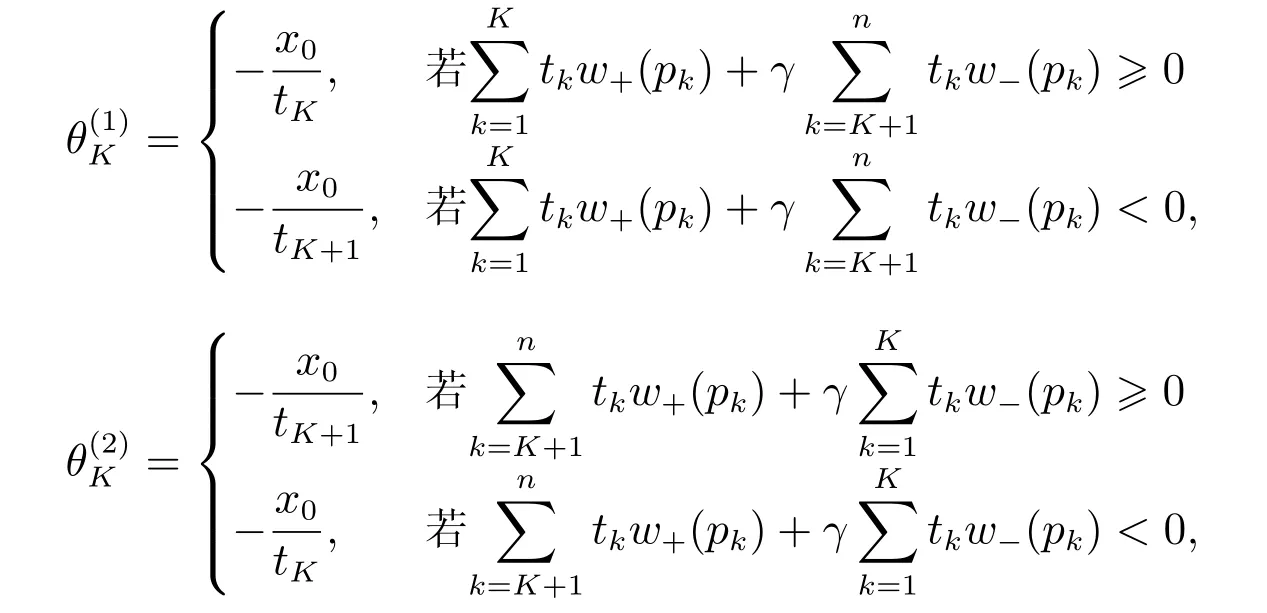

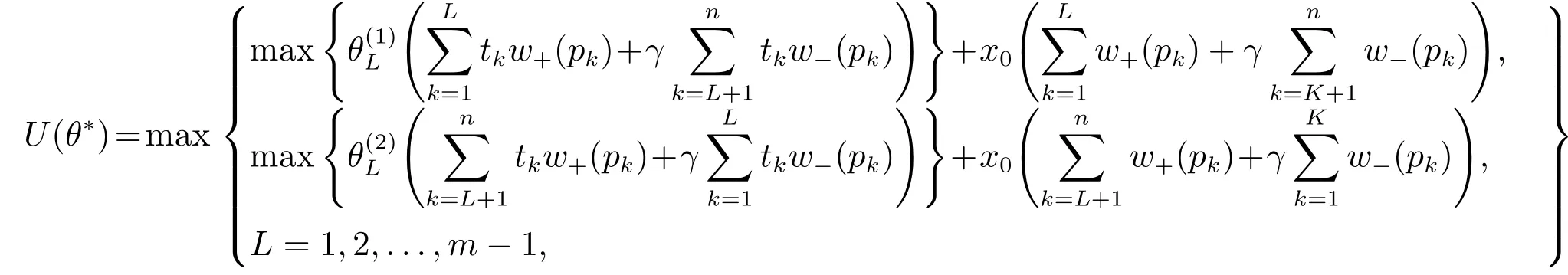

5 收敛性
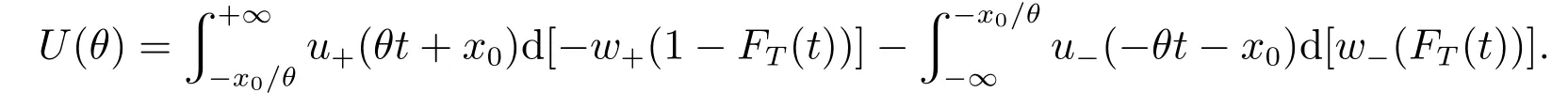
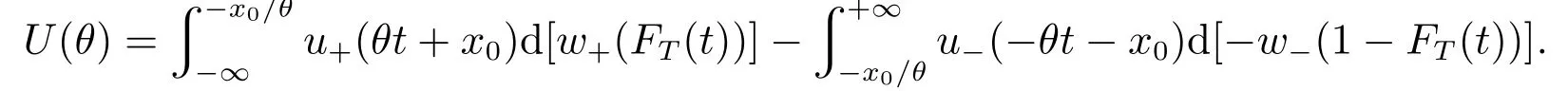

6 结束语
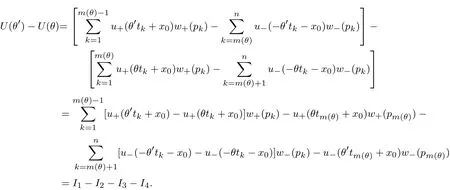
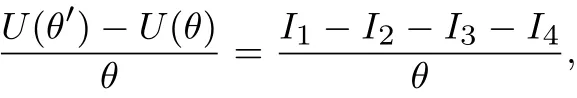
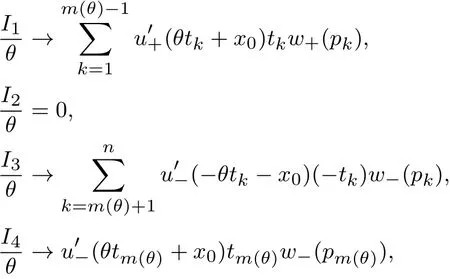
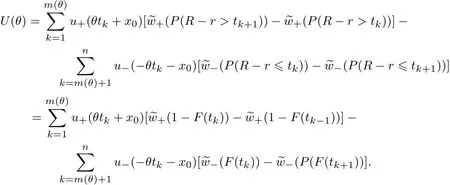







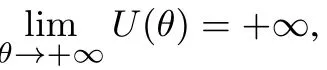

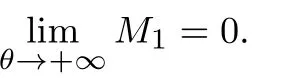


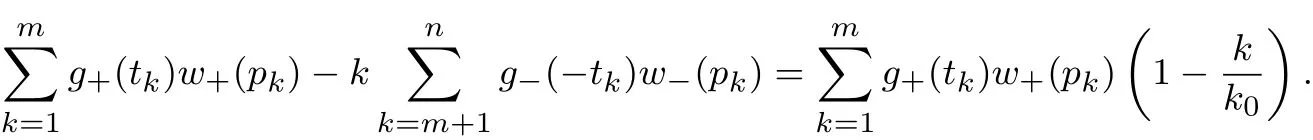

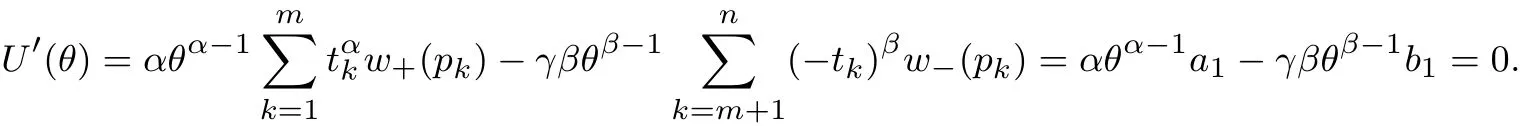
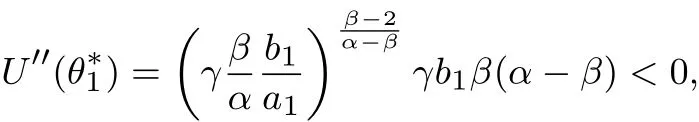


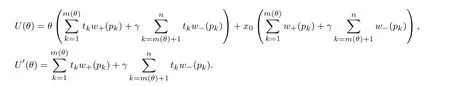
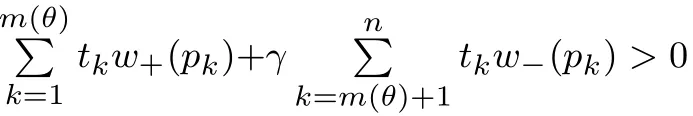
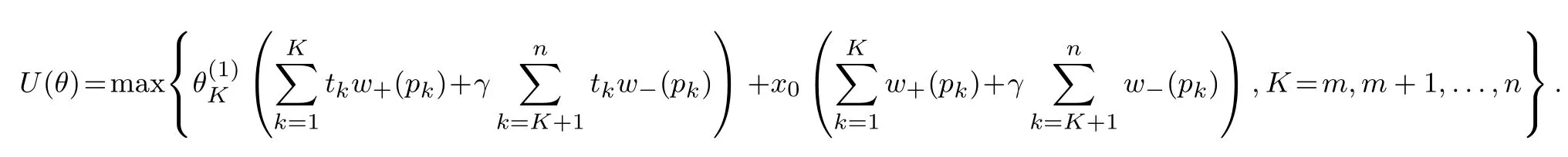
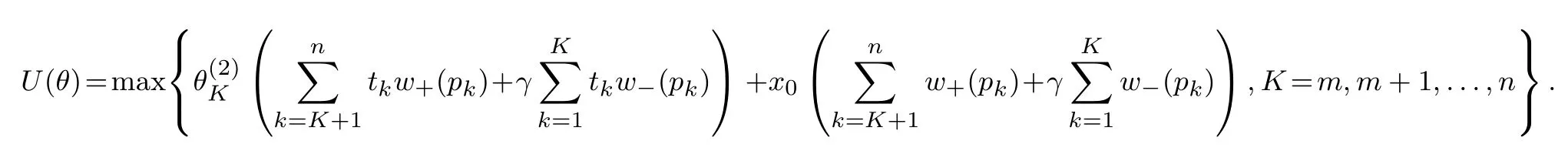

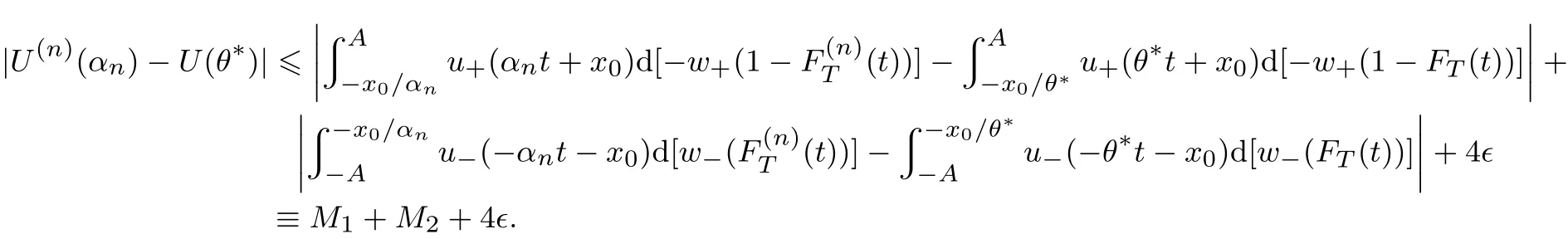
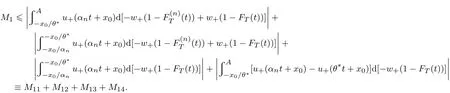
(1.School of Management,Fudan University,Shanghai 200433,China; 2.Financial Research Center,Fudan University,Shanghai 200433,China)
