基于多项式混沌理论的不确定度评定与分析
2015-10-25余学锋王亚梅赵婉丽
余学锋,于 杰,王亚梅,赵婉丽
(63870部队,陕西 华阴 714200)
基于多项式混沌理论的不确定度评定与分析
余学锋,于 杰,王亚梅,赵婉丽
(63870部队,陕西华阴714200)
针对基于ISO GUM提供的测量不确定度评估方法所存在的局限,提出了采用多项式混沌方法进行测量结果不确定度评估的新方法。分析了GUM测量不确定度评估方法所隐含的假设条件,给出了多项式混沌方法的测量不确定度评估原理。通过GUM与多项式混沌方法扩展不确定度包含因子估计误差的数值计算表明,当随机变量的PDF不满足高斯分布时,多项式混沌估计方法所获得的扩展不确定度更能反映实际情况。
计量学;多项式混沌;测量不确定度
1 引言
在许多高精度的专业测试中,存在着大量的不确定因素,会给测量结果带来不确定度。因此,在实际测量过程中除了要给出被测量的测量结果,还要给出测量结果不确定度,这就涉及到测量结果不确定度评定问题。关于测量不确定度评定的研究方向主要有两个方面:一是如何从已有可靠数据中,参数化地估计随机变量本身的不确定性,即随机变量是否服从某种分布;二是测量过程中的各个不确定度分量对最终测量结果的影响程度,即不确定度的传播。虽然大量的工程经验表明,测量过程中的随机变量往往是服从某种概率分布的,但是要确定其分布规律,则需要进行大量的辅助实验和统计处理,这需要慢慢积累。因此,目前的分析工作主要关注于第二方面,即认为含有随机变量的测量过程是随机过程,其随机变量是服从一定已知概率分布的。
目前,测量结果不确定度的评定一般是采用ISO GUM提供的方法[1]。对各不确定度分量,分别采用A类及B类方法进行评定。对获得的每个不确定度分量的标准偏差,再通过合成方差的方法得出合成不确定度,然后将合成不确定度乘以一个包含因子,得到扩展不确定度。根据GUM方法计算的测量结果不确定度,隐含了两个假设[2]:一是在不确定度合成时,采用的不确定度传播定律,其各不确定度分量是以一阶泰勒级数近似值为依据,如果不确定度传播关系的非线性明显,则泰勒级数展开式中的高阶项必须记入合成不确定度;二是扩展不确定度中的包含因子选择,是依据中心极限定律,认为即使所有的不确定度分量不都为正态分布,仍将合成不确定度的分布看成是正态分布。而如果某一不确定度分量为非正态分布,且其标准偏差较大时,合成不确定度的分布就不是正态分布。
对此,有学者提出了一些解决方法,如高阶矩(HOM)方法[3]。该方法在通常情况下,不确定度估计与GUM方法一致,在不满足GUM方法假设条件时,高阶矩方法将获得更高的估计精度。但高阶矩方法比较复杂,实际使用困难。
近年来,基于谱分析的测量不确定度评估方法开始引起人们的注意。多项式混沌方法(PCT,Polynomial Chaos Theory)便是其中之一。该方法最早由Wiener提出,在解决流体动力学、电路仿真、环境与声场等方面得到了较好的应用[4]。本文把多项式混沌方法引入测量结果不确定度评估中,通过构造多项式混沌空间以及数值计算分析,表明该方法可有效减少GUM近似假设而导致的评估误差。
2 测量不确定度与多项式混沌理论
2.1基于ISO GUM的测量不确定度描述
在多数情况下,测量结果可看作是一个随机变量,其与多个不确定分量有关,可描述为:Y=f(X1,X2,…,Xn),式中Y为测量结果的随机变量,通过与输入估计值Xi形成的关系式得到。Xi为具有一定概率分布的不确定分量,其分布参数可在现行的测量过程中直接确定,或通过外部信息(如技术手册)引入测量过程来确定。
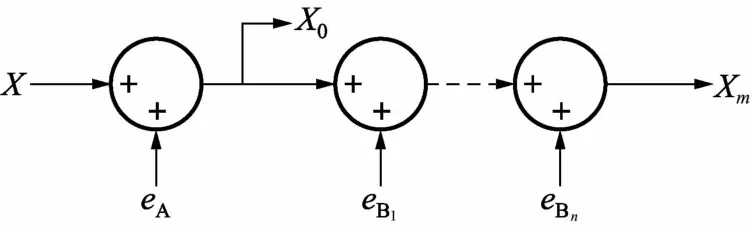
图1 不确定度的一般描述
在GUM中不确定度的一般描述如图1所示。把测量过程作为一个随机过程,变量eA和eB1,eB2,…,eBn均为不含系统误差相互独立具有各自的PDF分布函数的不确定度分量。eA为采用不确定度A类方法获得的测量不确定度,eB1,eB2,…,eBn为采用不确定度B类方法获得的测量不确定度。对于测量过程M而言,其合成标准不确定度为XM。由随机过程的测量不确定度传播定律可以得到:
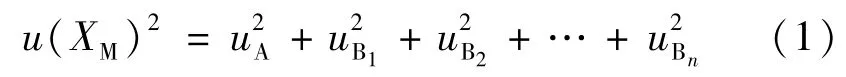
从式(1)可以看出,它是对测量过程的各项不确定度分量进行了简单的均方求和运算。式(1)及相关不确定度分量均以Y=f(X1,X2,…,Xn)的一阶泰勒级数近似值为依据,用来表示不确定度的传播。同时在计算扩展不确定度时,基于中心极限定律(CLT),用正态分布的标准偏差及对应的包含区间来描述。
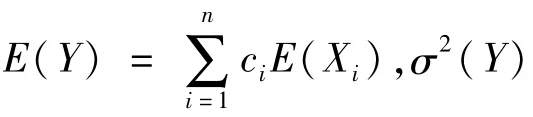
显然,有两种情况需要认真分析:一种情况是对于所描述的间接测量过程,当某些分量不是正态分布时,有可能出现σ2(Y)接近或不比其中某个分量的要大很多的情况;另一种情况是当间接测量不满足线性关系时,仍采用泰勒一阶展开多项式来描述不确定度传播规律就是不可接受的。
而对于上述两种情况,本文将尝试用PCT方法给予解决。结合实际工程应用,重点放在测量过程的不确定度分量为非正态分布,且不满足合成不确定度远大于任何一个不确定度分量条件时,其不确定度传播规律及相应的包含因子和包含概率关系。
2.2多项式混沌理论概述
多项式混沌理论是指采用多项式基所构成的随机空间来描述和传播(合成)具有PDF形式的随机变量的不确定度。其基本思想是用含独立随机变量的正交多项式混沌之和来近似表示随机过程,其关键步骤在于确定每个多项式的系数。对于很多复杂模型,多项式混沌展开的系数可以通过系统在某些配置点的输出来计算。配置点使用正交配点法来计算,与比多项式混沌展开阶次高一次的多项式之根相对应[5]。
在一个概率空间中,对于任意样本空间上的n个随机变量,采用多项式混沌展开逼近来描述该随机过程空间,其解析式为[6]:
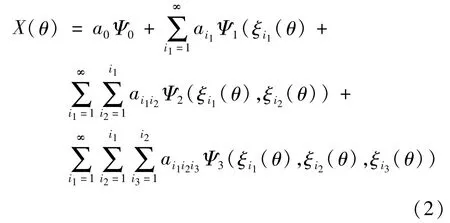
式中,X为待分析的随机过程,ai为展开多项式的系数,Ψi为所选择的多项式基,ξi1为不确定度分量的概率密度函数(PDF)所对应的多项式基展开式的随机变量。根据Askey法则,对应不同的概率密度函数,存在不同的最优多项式。对于概率密度函数为正态分布的随机变量,其最优多项式为埃尔米特(Hermite)多项式。对于概率密度函数为均匀分布的随机变量,其最优多项式为勒让德(Legendre)多项式[7]。
一般来说,任何一种概率密度函数都可以用完整的多项式混沌展开基构成的随机空间来描述。但在工程实际中,用多项式混沌逼近来描述式(2)所给出的随机(过程)空间中概率密度函数,其所形成的随机空间必须限制在有限的维数内,而这有限维数的选择不但与独立的不确定分量个数nv,即用于描述随机过程系统中随机空间独立变量ξ的个数有关,同时也与所选择的多项式基的最高阶数np有关。当给定nv和np的值后,则描述随机过程中每一个变量所需的多项式展开式的项数,可由下式来确定[8]:

式中,np为所选多项式基的最高阶数,nv为随机变量的个数。采用不高于p阶的多项式进行有限项截断并写成紧凑形式有:
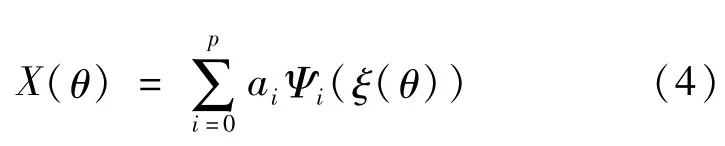
一般称式(4)为多项式混沌。其中,Ψi是根据nv个随机变量和np个最大阶数计算所得到的p个多项式基。ai是第i个多项式基所对应的系数,对于概率密度函数已知的随机变量,式中的系数为确定值。根据Askey法则,对应于不同的概率密度函数,存在不同的最优多项式,当权函数与概率密度函数相同时,展开式按指数收敛于随机变量[9]。
对于测量过程而言,测量不确定度分量的概率密度函数主要有两种,即正态分布和均匀分布。若随机变量ξ为具有零均值的标准正态分布,则展开的多项式基为埃尔米特(Hermite)多项式。若随机变量ξ为具有-1到+1的均匀分布,则展开的多项式基为勒让德(Legendre)多项式。根据Legendre多项式和Hermite多项式的递推关系,可以得到Hermite多项式基的前6级表达式为:H0(x)=1,H1(x)=x,H2(x)=x2-1,H3(x)=x3-3x,H4(x)=x4-6x2+3,H5(x)=x5-10x3+15x;勒让德(Legendre)多项式基前6项表达式为:P0(x)=1,P1(x)=x,P2(x)=1.5x2-0.5,P3(x)= 2.5x3-1.5x,P4(x)=4.375x4-3.75x2+0.375,P5(x)=7.875x5-8.75x3+1.875x。显然,采用多项式混沌方法进行测量不确定度表达,其关键就在于如何选择多项式基以及确定多项式的维数。
3 多项式混沌方法的测量不确定度表达
3.1不确定度分量的多项式混沌空间



事实上,对于分布函数或概率密度函数已知的随机变量,展开式的系数为确定值。随机变量的分布函数或概率密度函数由要求解的实际问题决定,其分布参数为已知。下面将用两个例子来说明多项式混沌理论如何表达测量不确定度以及如何弥补GUM方法的不足。
3.2GUM与PCT测量不确定度估计误差


根据前面的分析,PDF为均匀分布时,其多项式展开为采用Legendre多项式基的二阶单变量多项式,两个不确定度分量,按照Legendre多项式展开后就变为三项[10]。
显然,通过对两个为均匀分布的不确定度分量合成,可以得到其扩展不确定度包含因子与包含概率间的一系列对应关系。按照采用混沌多项式展开后进行计算,得到一组不同包含概率下对应的包含因子。同时按照GUM的方法,其合成不确定度的概率密度函数仍按照高斯分布处理,也可得到一组不同包含概率下对应的包含因子。将这些数据分别与理论分析结果(合成不确定度的PDF为三角分布)不同包含概率下对应的包含因子相比较,它们的相对误差分布情况如图2所示。从图中可以看出,当不确定度分量不满足高斯分布条件时,仍按照GUM方法进行不确定度合成,其扩展不确定度因子与理论值的偏差较大,除了在包含因子为2这个点。而采用多项式混沌展开方式得到的合成不确定度,其扩展不确定度包含因子与理论值的偏差较小。

图2 GUM和PCT计算扩展不确定度包含因子与理论值的相对误差
4 GUM与PCT方法的数值比较
前面分析了两个均匀分布随机变量不确定度的合成,对PCT与GUM方法得到的合成不确定度包含概率以及对应的包含因子通过图形给予了说明。下面将选择更复杂的一种情况,利用数值计算合成不确定度以及在不同包含概率下对应的包含因子,进一步了解PCT与GUM方法在描述扩展不确定度方面的效果。方法如下:
考虑有3个随机变量的不确定度合成,这3个随机变量的分布分别为一个正态分布,两个均匀分布。不确定度合成模型如图3所示。A1代表A类不确定度概率分布,其概率密度函数为正态分布,所对应的最优多项式逼近为Hermite多项式。B1、B2分别代表B类不确定度概率分布,其概率密度函数为均匀分布,所对应的最优多项式逼近为勒让德(Legendre)多项式,D1代表合成不确定度概率分布。

图3 GUM方法测量不确定度评估模型
此时,合成不确定度多项式混沌空间,用不高于p阶的多项式进行有限项截断所对应的多项式基的系数描述如下式:

从理论上分析上述不确定度模型,其合成不确定度的概率密度函数为近似三角形分布。对式(8)按照多项式混沌理论进行不确定度合成,其合成不确定度的概率密度函数也近似为三角分布。而按照GUM的理论,其合成不确定度的概率密度函数仍默认为正态分布。对于这些差异通过数值计算,可以有较为清晰的了解。
分别用GUM和PCT方法计算图3不确定度模型下的扩展不确定度的包含因子及对应的包含概率:
(1)首先对各个不确定度分量,按照GUM指南方法进行不确定度合成,获得方差(x)和标准偏差σt(x),根据GUM指南所假设条件,即合成不确定度的概率密度分布满足中心极限定律,计算扩展不确定度的包含因子以及对应的包含概率。
(2)然后对各个不确定度分量,按照多项式混沌展开方法对其PDF进行重构,计算合成不确定度的方差(x)和标准偏差σp(x),根据多项式混沌理论计算扩展不确定度的包含因子以及对应的包含概率。
设计两组数据,第1组数据为:设定A类不确定度分量的PDF为正态分布,分布参数,期望E= 1,标准偏差为0.3。B类不确定度分量的PDF为均匀分布,分布参数,期望E=0,标准偏差为1/,GUM和PCT方法计算结果见表1。而根据GUM指南方法计算获得的合成不确定度为:σt(x)=0.983 2。由于合成不确定度值要远大于B类不确定度分量的标准偏差,因此满足中心极限定律假设条件,其按照正态分布计算的扩展不确定度包含因子及对应的包含概率与理论值相近。而采用多项式混沌方法计算获得的合成不确定度为:σt(x)=0.864 3,扩展不确定度包含因子及对应的包含概率与理论值也表现出良好的一致性。
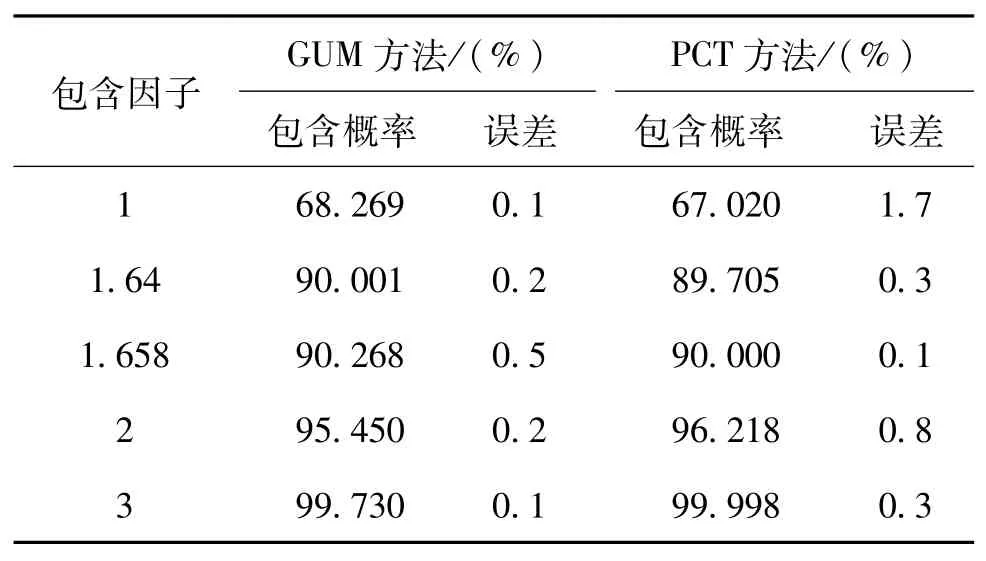
表1 第1组数据情况下计算结果
第2组数据:设定A类不确定度分量的PDF为正态分布,分布参数为:期望E=1,标准偏差为0.1。B类不确定度分量的PDF为均匀分布,分布参数为:期望E=0,标准偏差为0.2/,GUM和PCT方法计算结果见表2。而根据GUM指南方法计算获得的合成不确定度为:σt(x)=0.19148。由于合成不确定度值接近B类不确定度分量0.115 5,因此不能完全满足中心极限定律假设条件,但仍按照正态分布来计算扩展不确定度包含因子及对应的包含概率,可以看出与理论值出现较大偏差。同样的不确定度分量,采用多项式混沌方法计算扩展不确定度包含因子及对应的包含概率,与理论值比较接近,表现出良好的稳定性。

表2 第2组数据情况下计算结果
实际上,当合成不确定度值接近某一B类不确定度分量值情况下,合成不确定度的概率密度函数近似为三角分布,而不是GUM所假设的正态分布,因此,采用GUM方法进行不确定度合成,得到的扩展不确定度其包含因子所对应的包含概率就会出现较大的偏差。
5 结论
(1)在大多数情况下,基于多项式混沌的不确定度分析方法与采用ISO(GUM)分析方法得出的结果相一致,这也说明多项式混沌方法完全可以应用于测量不确定度评估中。相比而言,多项式混沌方法具有更好的灵活性和更强的适应性。
(2)当测量过程中随机变量PDF分布与理论假设不相符时,或不满足中心极限定律条件时,采用GUM方法进行不确定度合成并计算扩展不确定度时可能带来较大的偏差,而根据多项式混沌方法所获得的扩展不确定度更能反映实际情况。
(3)假如对不确定度分量的概率分布未知,按照GUM方法来处理,就有可能会出现扩展不确定度的计算误差跳动的现象。而按照PCT方法来处理,扩展不确定度的计算误差变化就相对平稳。显然当不确定度分量的概率分布难以确定时,采用PCT方法来处理,其扩展不确定度的估计更为稳健。
[1]ISO/IEC:Uncertainty of measurement—Part 3:Guide to the expression of uncertainty in measurement[S].2008.
[2]国家质量监督检验检疫总局.JJF 1059.1-2012测量不确定度评定与表示[S].2012.
[3]D'Antona G.Expanded uncertainty and coverage factor computation by higher order moments analysis[C]// IMTC 04.Proceedings of the 21st IEEE,Vol.1,234-238.
[4]王晓东,康顺.多项式混沌方法在随机方腔流动模拟中的应用[J].中国科学,2011,41(6):790-798.
[5]皮霆,张云清,吴景铼.基于多项式混沌方法的柔性多体系统不确定性分析[J].中国机械工程,2011,22 (19):2341-2343.
[6]Dongbin Xiu,Karniadakis G E.Modeling uncertainty in flow simulations via generalized polynomial chaos[J].Journal of Computational Physics,2003,187:137-167.
[7]Finette S.A stochastic representation of environmental uncertainty and its coupling to acoustic wave propagation in ocean waveguides[J].Journal of the Acoustical Society of America,2006,120(5):2567-2579.
[8]Lacor C,Smirnov S.Uncertainty propagation in the solution of compressible Navier-Stokes equations using polynomial chaos Decomposition[C]//NATO RTO AVF -147 Symposium on“Computational Uncertainty in Military Vehide Design”,Athens,Grecce,2007,1-13,48.
[9]H J威佛,中德·王(数学).离散和连续傅里叶分析理论[M].北京:北京邮电学院出版社,1991.216-219.
[10]薛毅.数值分析与科学计算[M].北京:科学出版社,2011.271-280.
Measurement Uncertainty Evaluation and Analysis Based on Polynomial Chaos Approach
YU Xue-feng,YU Jie,WANG Ya-mei,ZHAO Wan-li
(PLA 63870 Unit,Huayin,Shaanxi 714200,China)
Deal with the limitations of measurement uncertainty evaluation method based on ISO GUM,A new approach to the evaluation of measurement uncertainty based on the polynomial chaos theory is presented.The main assumptions behind the measurement uncertainty propagation based on the GUM is analyzed.The measurement uncertainty evaluation used the PCT approach is provided.By the GUM and PCT method,the relative absolute difference between the confidence obtained in the two cases and the true value is computed.It is show that in case of a distribution very different from the Gaussian,the polynomial approach leads to results very close to the ideal case.
Metrology;Polynomial chaos;Measurement uncertainty
TB9
A
1000-1158(2015)01-0107-06
10.3969/j.issn.1000-1158.2015.01.23
2013-06-14;
2013-11-27
余学锋(1963-),男,江苏南京人,63870部队高级工程师,主要研究方向为仪器仪表与计量测试。yxfyd@163.com
