基于LMD和局域时频熵的旋转机械故障诊断方法

孟 宗，李姗姗，王亚超

（1.燕山大学电气工程学院，河北　秦皇岛　066004；2.河北省测试计量技术及仪器重点实验室，河北　秦皇岛　066004）

基于LMD和局域时频熵的旋转机械故障诊断方法

孟 宗1，2，李姗姗1，2，王亚超1，2

（1.燕山大学电气工程学院，河北秦皇岛066004；2.河北省测试计量技术及仪器重点实验室，河北秦皇岛066004）

提出了一种基于局部均值分解和局域时频熵的旋转机械故障诊断方法。以旋转机械作为研究对象，利用LMD方法分解旋转机械振动信号，对分解得到的各乘积函数进行Hilbert变换，得到振动信号的时频分布。为了定量描述振动信号能量的时频分布情况，提出了局域时频熵的概念，根据旋转机械故障的频谱特征，将整个时频平面划分为若干时频段，计算时频段的局域时频熵，以局域时频熵作为旋转机械故障特征，实现旋转机械故障特征提取。基于局域时频熵进行故障特征提取可以细致地反映各时频区域能量分布的差别，同时可以减小计算量，提高运算速度。仿真与实验结果表明，该方法能有效地应用于旋转机械故障诊断中。

计量学；旋转机械；故障诊断；局域时频熵；局部均值分解

1　引言

旋转机械是应用非常广泛的一类机械设备，其应用覆盖了电力、石化、冶金、航空航天、机械制造等工程领域。随着科学技术和现代工业的飞速发展，旋转机械设备日益朝着大型化、连续化、自动化和大功率、大载荷等方向发展，其工况不仅影响该机械设备本身的安全运行，而且还会对后续生产和运行造成直接影响，故障严重时会造成巨大的经济损失，甚至会导致机毁人亡的事故。因此，对旋转机械工作状况进行实时监测和故障诊断的研究越来越受到人们的重视［1，2］。

旋转机械设备运行时，其振动信号多为非平稳非线性的多分量信号，特别是在出现故障的情况下，具有明显的非线性非平稳特性，传统的信号分析方法不再适用；时频分析技术的发展为振动信号分析提供了一些新的途径。常用的时频分析方法有短时傅里叶变换、Wigner分布、小波变换、经验模态分解等，然而它们均存在一定的局限性。经验模态分解是一种自适应的信号处理方法，该方法虽然在机械故障诊断等领域得到了广泛应用［3，4］，但仍存在过包络、欠包络、模态混叠、端点效应、计算瞬时频率时产生负频率等问题［5，6］。

2005年，Smith J S首次提出了一种新的自适应非平稳信号的分析方法——局部均值分解（Local Mean Decomposition，LMD）方法［7］。由于机械工程领域存在大量的非平稳信号，而这些非平稳信号大多是调制信号，对于这些信号，解调是一种有效的分析方法，采用LMD方法对机械故障振动信号进行分解，提取各个分量的瞬时幅值和瞬时频率，实际上就是对振动信号进行解调，能够得到信号完整的时频分布，从而可以有效地提取出振动信号的特征。目前，LMD方法在生物医学［7］、旋转机械故障诊断［8～10］等领域迅速得到应用。

信号的时频分布是描述信号在采样时间内各个频率处的能量变化，同一机械设备在不同的工作状态下的时频分布往往发生变化，为了定量描述这种变化程度，本文提出了一种基于LMD的局域时频熵旋转机械故障诊断方法。首先利用LMD方法分解机械振动信号，将得到的各乘积函数（Product Function，PF）分量进行Hilbert变换，以得到振动信号的时频分布，然后划分时频块计算局域时频熵，通过熵值判断机械的工作状态和故障类型。

2　LMD的基本原理

LMD方法可以从原始信号中分离出纯调频信号和包络信号，将纯调频信号和包络信号相乘即可得到一个瞬时频率具有物理意义的PF分量，重复该过程，直至所有的PF分量都被分离［10］。因此LMD方法可以自适应地将一个复杂的非平稳的多分量信号分解为若干个瞬时频率具有物理意义的乘积函数PF之和，其中每一个PF分量由一个包络信号和一个纯调频信号直接求出。包络信号是该PF分量的瞬时幅值，而PF分量的瞬时频率则可以由纯调频信号直接求出，进一步将所有PF分量的瞬时幅值和瞬时频率组合，便可以得到原始信号的完整的时频分布。LMD的分解过程见文献［11］。

3　局域时频熵

旋转机械发生故障时，振动信号会发生变化，这种变化主要表现在振动信号的能量随时间和频率的分布产生变化，时频分布是对信号能量的精确表示，从时频谱图中可以分析出故障振动信号的能量随时间和频率的分布情况，为了定量描述这种分布情况，将信息熵理论引入时频分布，提出了时频熵的概念［12，13］。

不同信号在时频分布上的差异表现为时频平面上不同的小块时频段的能量分布的差异，各时频区能量分布的均匀性则反映了机器运行状态的差别，信息熵是概率分布均匀程度的度量，将时频平面等分为n个面积相等的时频块，见图1，每块内的能量为Wk（k=1，…，n），整个时频平面的能量为A，对每块进行能量归一化，得到qk=Wk/A，于是就有，符合计算信息熵的初始归一化条件，仿照信息熵的计算公式，信号的时频熵的计算公式为

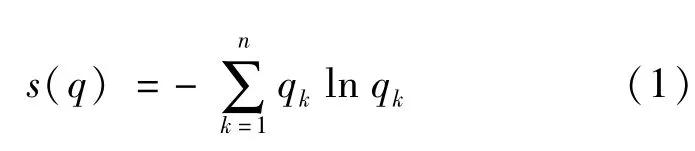
时频熵给不同状态下信号的时频分布提供了一个量的度量，通过计算信号的时频熵，可以判断出信号所代表的机械运行状态。然而，实际振动信号的频率成分比较多，得到的时频分布比较复杂，分析计算信号整体的时频熵值可能不足以细致地反映系统真实的运行状态。因此，本文提出了局域时频熵的概念，首先基于故障机理分析，根据不同类型故障的频谱特征，将整个时频平面划分为若干时频段，见图1，将每一个时频段的时频熵定义为局域时频熵。第h时频段的局域时频熵定义为

式中，i=1，…，K；j=1，…，L；K×L=n。

计算某时频段内的局域时频熵s1（q），s2（q），…，sk（q），以局域时频熵作为旋转机械故障特征，通过分析特定频段的局域时频熵的变化进行旋转机械故障诊断。本文提出的基于局域时频熵的旋转机械故障诊断方法的优势在于，一方面局域时频熵可以细致地反映了各时频区域能量分布的差别，从而提高旋转机械故障诊断准确率；另一方面可以减小计算量，降低运算时间，从而提高旋转机械故障诊断实时性。

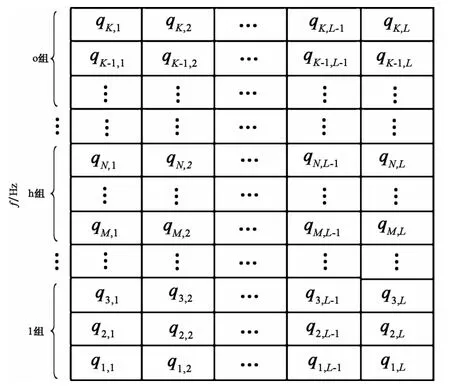
图1　时频平面等分示意图

4　仿真研究

构造一个模拟仿真信号，该信号是由调幅频率10 Hz，基频30 Hz，调频频率15 Hz的调频调幅信号和频率为150 Hz的正弦信号叠加，表达式为其时域波形图见图2。

图2　信号时域波形图

采用局部均值分解方法对振动信号进行分解，得到4个PF分量和1个余量，见图3，做出其时频谱，见图4，振动信号的能量集中在特征频率30 Hz 及150 Hz频段处。

将图4所示时频平面等分为16384个时频块，在能量比较集中的30 Hz及150 Hz附近划分时频段，分别命名为时频段1、2，计算局域时频熵值，见表1。时频段1和时频段2的熵值大小相近，说明在30 Hz及150 Hz附近的时频段能量分布比较均匀，这与图4所示的时频谱图相一致。信号局域时频熵值之和（为5.648 8）占总时频熵值的98.98％，几乎没有能量的损失。因此，本文提出的基于LMD的局域时频熵的故障特征提取方法是有效的。

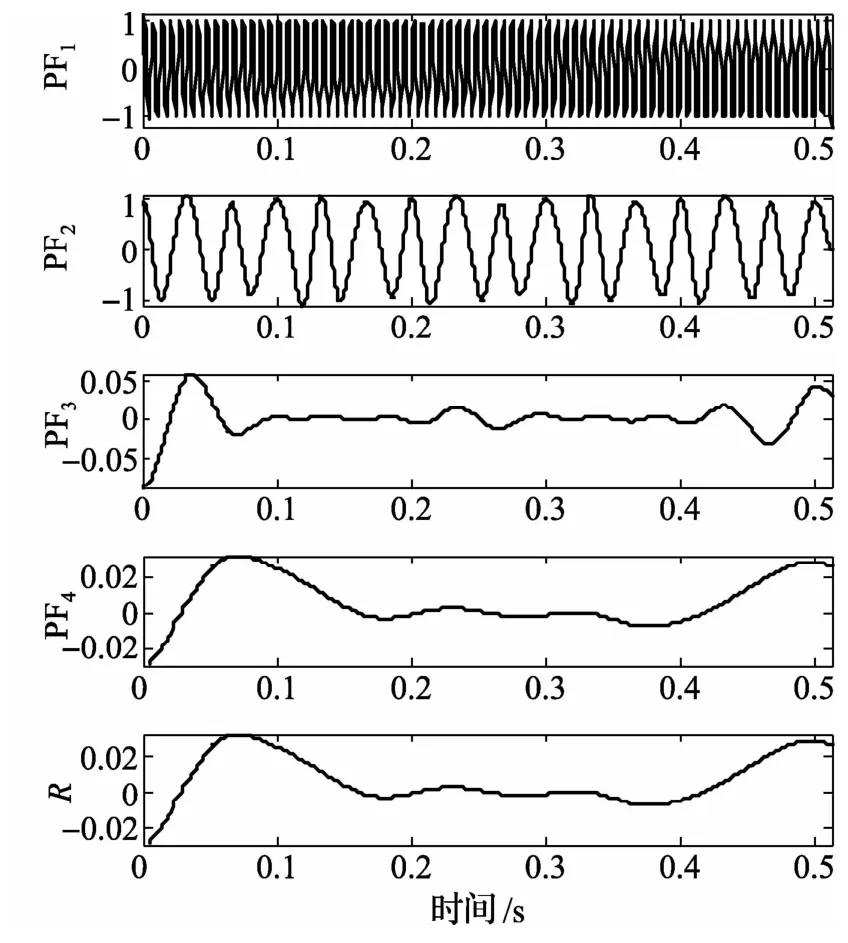
图3　LMD分解结果图

图4　时频谱图

表1　时频熵值

5　实验研究

设定轴承故障模拟试验台的转子转速为1 725 r/min，模拟轴承外圈单点电蚀故障，故障尺寸为0.007 inches，采样频率为2048 Hz，轴承外圈故障特征频率为103.3 Hz，转轴基频为28.75 Hz。采集一组正常轴承振动加速度信号和一组轴承外圈故障振动加速度信号，分别见图5、图8，可以看出故障信号振幅增大，且出现周期性冲击成分。

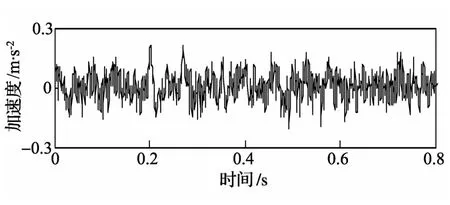
图5　正常轴承振动加速度信号时域波形图

本文中采用局部均值分解方法对正常轴承振动信号进行分解，得到4个PF分量和1个余量，见图6，做出其时频谱，见图7，振动信号的能量在整个时频平面内比较分散。将采集到的故障振动信号进行如上处理，得到5个PF分量和1个余量，见图9，做出其时频谱，见图10，振动信号的能量集中在故障特征频率（103.3 Hz）及其二倍频（206.6 Hz）、转轴基频的20倍频（575 Hz）频段处。

图6　正常轴承局部均值分解结果图

分别将图7、图10所示时频平面等分为262144个时频块，在能量比较集中的103.3 Hz、206.6 Hz 及575 Hz附近划分时频段，分别命名为时频段1～3，计算局域时频熵值。轴承正常工作状态和存在外圈故障状态下时频熵（称之为全局时频熵）变化情况及时频段1、2的局域时频熵的变化情况见表2。正常轴承的时频熵值比故障状态下振动信号的时频熵值大，与时频分析中能量分布相对应，这与最大熵原理是一致的；进一步，相比于正常状态，轴承的故障特征频率（时频段1）及其二倍频（时频段2）附近的局域时频熵值明显减小，可以判断轴承外圈发生了故障。由表2可以看出，虽然轴承出现外圈故障时全局时频熵也发生了变化，但是变化特征并不明显，而且通过全局时频熵不能判断出故障的类型。基于此，通过对比局域时频熵值的大小，可以判断轴承的工作状态。

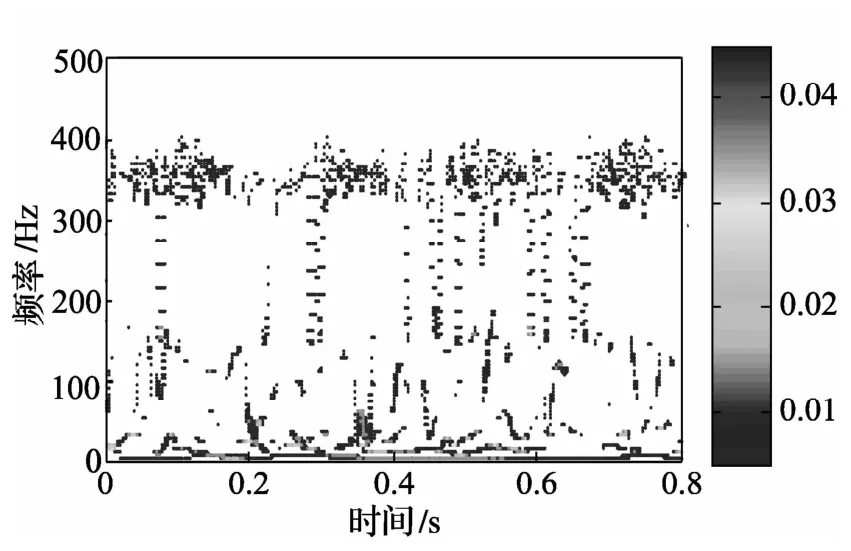
图7　正常轴承时频谱图

图8　外圈故障轴承振动加速度信号时域波形图

图9　外圈故障轴承局部均值分解结果图

图10　外圈故障轴承时频谱图

表2　外圈故障轴承时频熵值

6　结论

本文研究了一种基于局部均值分解和局域时频熵旋转机械故障诊断方法。利用局部均值分解方法处理旋转机械振动信号，对分解得到的各乘积函数进行Hilbert变换，得到振动信号的时频分布。针对不同故障状态振动信号在时频分布上能量分布的差异性，将时频熵理论应用到故障特征提取中，通过计算时频熵判断机械运行状态。由于实际振动信号时频分布比较复杂，分析全局时频熵值不仅增加计算量、影响计算时间，而且全局时频熵值不足以细致地反映机械设备的运行状态，基于此，本文研究了一种基于局域时频熵的旋转机械故障特征提取方法，并应用于轴承故障诊断中。数值仿真和轴承故障诊断实例的结果表明，基于LMD的局域时频熵特征提取方法能有效地应用于旋转机械故障诊断中。

［1］钟秉林，黄仁.机械故障诊断学［M］.3版.北京：机械工业出版社，2007.

［2］韩捷，张瑞林.旋转机械故障机理及诊断技术［M］.北京：机械工业出版社，1997.

［3］孟宗，顾海燕，刘利晖，等.基于EMD与AR谱的轧机主传动系统故障诊断研究［J］.计量学报，2011，32 （4）：338-342.

［4］谢平，王欢，杜义浩.基于EMD和Wigner-Ville分布的机械故障诊断方法研究［J］.计量学报，2010，31 （5）：390-394.

［5］汤宝平，董绍江，马靖华.基于独立分量分析的EMD模态混叠消除方法研究［J］.仪器仪表学报，2012，33 （7）：1477-1482.

［6］杜陈艳，张偷锋，杨平，等.经验模态分解边缘效应抑制方法综述［J］.仪器仪表学报，2009，30（1）：55-60.

［7］Smith J S.The local mean decomposition and its application to EEG perception data［J］.Journal of the Royal Society Interface，2005，2（5）：443-454.

［8］Yang Y，Cheng J S，Zhang K.An ensemble local means decomposition method and its application to local rubimpactfaultdiagnosisoftherotorsystems［J］.Measurement，2012，45（3）561-570.

［9］鞠萍华，秦树人，赵玲.基于LMD的能量算子解调方法及其在故障特征信号提取中的应用［J］.振动与冲击，2011，30（2）：1-4.

［10］程军圣，张亢，杨宇.局部均值分解方法及其在滚动轴承故障诊断中的应用［J］.中国机械工程，2009，20 （22）：2711-2717.

［11］孟宗，王亚超，王晓燕.基于局部均值分解和极值延拓的旋转机械故障特征提取方法［J］.计量学报，2014，35（5）：469-473.

［12］林京，屈梁生.信号时频熵及其在齿轮裂纹识别中的应用［J］.机械传动，1998，22（2）：37-39.

［13］于德介，张嵬，程军圣，等.基于EMD的时频熵在齿轮故障诊断中的应用［J］.振动与冲击，2005，24（5）：26-29.

Method of Rotating Machinery Fault Diagnosis Based on LMD and Local Time-frequency Entropy

MENG Zong1，2，LI Shan-shan1，2，WANG Ya-chao1，2
（1.Institute of Electrical Engineering，Yanshan University，Qinhuangdao，Heibei 066004，China；2.Key Laboratory of Measurement Technology and Instrumentation of Hebei Province，Qinhuangdao，Heibei 066004，China）

A method based on LMD（Local Mean Decomposition）and local time-frequency entropy in rotating machinery fault diagnosis is proposed.Aiming at bearing，the vibrating signal is decomposed into PFs（Product Functions）by LMD，and then Hilbert transformation is applied to every PF to get time-frequency distribution.The local time-frequency entropy is introduced to study the energy in time-frequency distribution quantitatively.In detail，according to the spectrum characteristic of bearing fault，the whole time-frequency plane is divided into some segments，and whose entropies are calculated to extract the fault feature of the bearing.By the method of fault feature extraction based on local time-frequency entropy，differences among the segments could be reflected in large.Also the computational complexity is reduced at the same time.The results of simulation and experiment are presented to verify the theory analysis.

Metrology；Rotatingmachinery；Faultdiagnosis；Localtime-frequencyentropy；Localmean decomposition

TB936

A

1000-1158（2015）01-0077-05

10.3969/j.issn.1000-1158.2015.01.17

2013-06-09；

2014-07-25

国家自然科学基金（51105323）

孟宗（1977-），河北保定人，燕山大学教授，博士，主要研究方向为信号分析与处理、旋转机械故障诊断。mzysu@ysu.edu.cn