导波式雷达物位计测量误差分析与软件修正

刘 铮， 魏 萌， 徐科军

（合肥工业大学电气与自动化工程学院，安徽 合肥 230009）

导波式雷达物位计测量误差分析与软件修正

刘 铮， 魏 萌， 徐科军

（合肥工业大学电气与自动化工程学院，安徽 合肥 230009）

分析了导波雷达物位计测量误差产生的原因，提出软件修正方法。在硬件方面分析了发射脉冲宽度和等效时间采样间隔的影响；在软件方面分析了信号处理过程产生的粗大误差、随机误差和系统误差。基于现有的硬件平台，提出一整套处理方法以减小测量误差，包括结合回波特征参数去判断物位回波，9点移动平均滤波预处理，选取最小斜率点作为回波定位点，对计算值进行中位值平均滤波。水位测量实验结果表明，在理论误差为2～4 cm情况下，实际测量误差小于1 cm，这验证了软件修正方法的有效性。

计量学；导波雷达物位计；测量误差分析；软件修正

1　引 言

导波式雷达物位计作为新型物位测量仪表，广泛应用于石油、化工领域中水类、油类和固料类等的接触式测量［1-3］。由于导波杆对发射脉冲的汇聚导向作用，使电磁波能量更大程度地导向测量介质，因此，具有适用于小介电常数液位测量、受粉尘和泡沫等影响小的特点。根据准确度要求，雷达物位计可划分为过程控制级和贸易结算级，导波式雷达物位计属于过程控制级。

目前，国内文献大都侧重于介绍导波雷达物位计的工作原理和实际应用，研究测量准确度问题的文献较少。国外某些文献提出了提高测量准确度方法，产品的测量误差最小可至1 mm，而国内产品测量误差最小为1 cm。例如，使用不完全外部介电传输探测器的特制导波杆［4］，结合参考曲线的熵滤波法［5］，安装反射器［6］等。然而，国外的方法需要加装反射器和特定的导波杆或需要空罐参考曲线。

本文首先从硬件和软件两方面分析导播雷达物位计测量误差的来源，然后，从信号处理方法角度，提出修正导波式雷达物位计测量误差的方法，以提高其测量准确度。

2　误差分析

2.1硬件误差

导波雷达物位计依据时域反射原理测量物位。雷达主机的时基电路产生脉冲波形。该信号分为两路。一路经前置触发电路放大整形，变成幅度较大、前沿较抖的脉冲信号送至脉冲发射器；脉冲发射器通过发射天线沿导波杆发送周期性窄脉冲电磁波；电磁波在不同介质的分界面上反射后形成一系列回波信号，由接收天线接收后送往等效时间采样电路。另一路到采样脉冲发生器，产生采样脉冲，以控制等效时间采样电路。等效时间采样电路对回波信号进行采样，再将其变成中低频信号，送至单片机［7］。

导波雷达物位计硬件由脉冲发射电路、等效时间采样电路和信号处理电路3个部分组成，如图1所示。下面分析脉冲发射电路和等效时间采样电路所产生的误差。

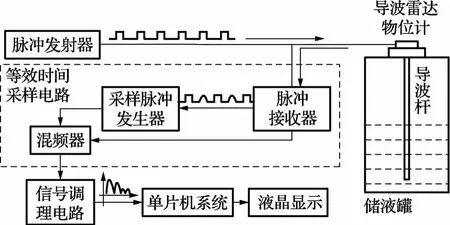
图1　硬件原理框图

（1）脉冲发射电路

根据雷达原理中雷达距离分辨率的定义可知，脉冲式雷达可分辨两目标间的最小距离为：

式中：ΔR为距离分辨率；c为电磁波在真空中的传播速度；τ为脉冲收发单元产生的发射脉冲的宽度。

可见，脉冲式雷达能分辨目标间的最小距离与发射脉冲的宽度有关。例如，某国产导波雷达物位计发射脉冲的宽度为15 ns，若空气中电磁波传播速度按光速计算，则ΔR=2.25 m。即在雷达脉冲波的传输途径中，间距小于2.25 m的两目标的反射回波将会产生混叠。接收的反射回波混叠程度越高，则对目标回波的分辨造成的影响也就越大，从而影响了测量的准确度。相关资料表明，德国E+H公司导波雷达物位计的发射脉冲宽度仅为0.8 ns。所以，发射脉冲的宽度会影响测量准确度［8］。通过减小发射脉冲宽度可提高距离分辨率，进而减弱回波信号的混叠程度，有利于测量准确度的提高。发射脉冲宽度越小，所包含的频率成分越多，因此反射回波波峰越陡，也有利于测量准确度的提高。

（2）等效时间采样电路

由于在测量过程中，脉冲信号的行程时间为ns量级，如果通过实时采样来直接测量时差，普通的单片机无法满足要求，所以，一般依据等效时间采样原理先对回波信号进行采样［9］，将高速信号在时域上放大，扩展成低速信号。等效时间采样方法的示意图如图2所示。

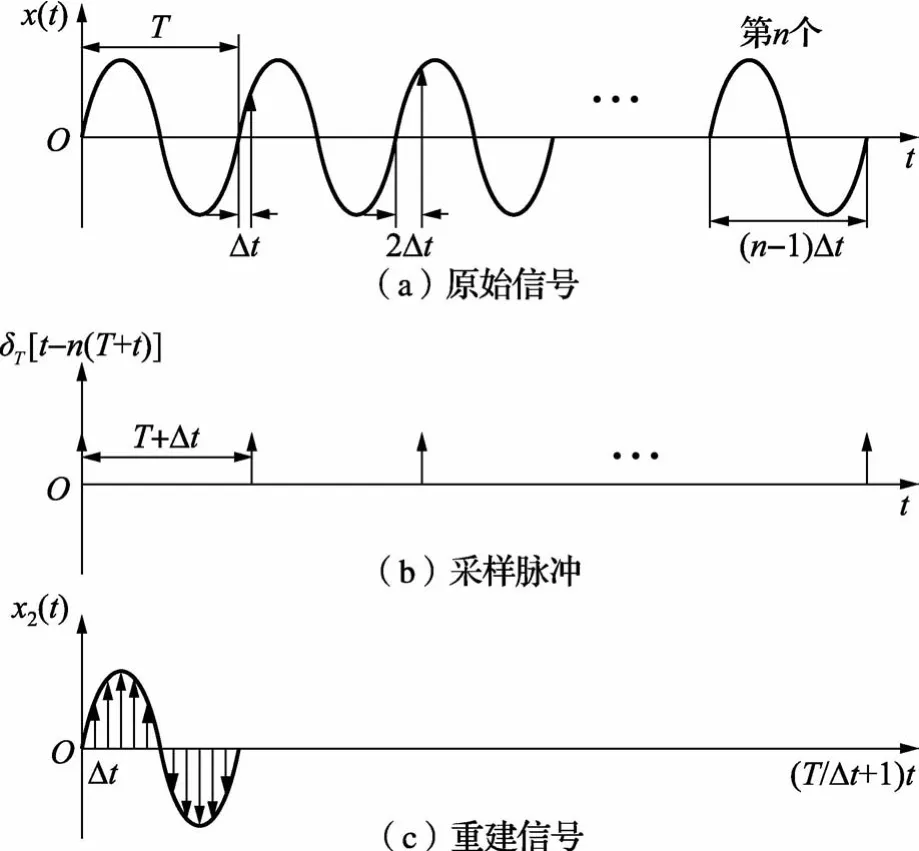
图2　等效时间采样原理示意图

设接收脉冲重复周期为T，两路脉冲间隔微小时间差为Δt，单片机采样频率为Fs，则等效时间采样放大倍数K为［10］：

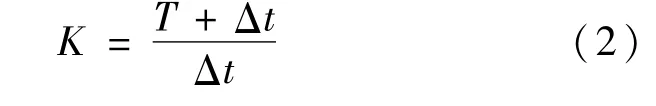
单片机采集经过等效时间采样电路转换和放大后的回波信号，其相邻采样点之间所对应的物位距离d为：

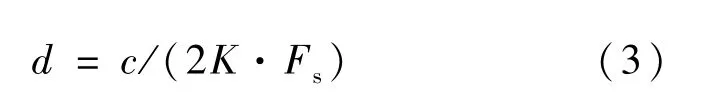
可见，提高等效时间采样电路的放大倍数K或者提高单片机采样频率Fs可以提高采样精度。由式（2）可知，要提高放大倍数K就要减小延迟时间Δt。例如，某国产导波雷达物位计采用447 kHz的发射脉冲频率，Δt为10 ps，Fs为50 kHz，所以，

另外，Δt的稳定性也会影响测量准确度。若Δt不够稳定，会导致等效放大倍数K的变化，从而导致在时域上拓展的回波波形的传播时间发生变化，这样会影响回波时间的计算准确度，从而影响测量准确度。

2.2软件误差

（1）粗大误差

信号处理中的粗大误差来源于物位回波判断错误和失波。前者主要是由信号处理方法造成，后者由硬件条件、环境等造成。

物位回波为介质表面反射回波。在采集的回波信号中，除物位回波外，还有由其它因素产生的反射回波，这些统称为噪声。以物位回波信号的频率作为参照，噪声可分为高频噪声和物位回波同频噪声两类。其中，高频噪声对应于白噪声的高频部分；因操作条件、电源干扰、仪器不稳定、障碍物产生的尖峰或突变信号等，被看成信号同频噪声。可见，若无法从各类噪声中区分物位回波，将造成对真实回波的误判，从而导致粗大误差。

传统方法以回波峰值点幅值最大［11，12］作为条件进行判断。然而，由于实际信号的复杂性，此方法条件单一，在出现干扰回波幅值较大的情况下会发生误判，造成粗大误差。

由于射频电路的不稳定、介质的强烈挥发或液面晃动等造成反射回波波形特别弱或消失，即所谓的“失波”，将导致无法确定物位回波或错误判断。

（2）随机误差

在导波雷达物位计的信号处理中可以看出，即使同一液位的测量值也并不稳定，呈现上下波动的特点，故存在随机误差。此外，在实验测量过程中，通过钢尺或米尺读取标准值，由于钢尺或米尺的精度限制，使读数中不可避免地存在随机误差。

（3）系统误差

信号处理中的系统误差主要存在于传播时间计算过程中。其中，回波定位点的选取是传播时间计算的关键。物位回波波形类似钟形曲线，具有一定的宽度，有峰值点、上升沿、下降沿。应当选择幅度相对稳定且随距离变化敏感的位置作为回波定位点。通常选择回波峰值点作为定位点。然而，由于信号本身分辨率不高，会导致即使是同一液位，峰值点也会出现1～2点的波动。根据式（5）可知，将导致1.34～2.68 cm的误差。此外，实际中会出现平顶峰波形情况，真实峰值点无法确定，导致在一段液位内确定的峰值点相同，也造成误差。

标准值若通过钢尺或米尺获得，则测量环境的温度会对尺子造成热胀冷缩，带来误差。此外，读数人员的读数习惯也会导致系统误差。

2.3其他因素误差

电路本身的设计和元器件的质量对输出高频信号的信噪比有直接影响。测量介质的介电常数直接影响回波波形。机械安装的影响主要在于障碍物干扰，障碍物产生反射信号，容易导致对被测介质反射信号的误判，从而增大错误测量的概率。

3　误差修正

从软件修正出发，研究合适的信号处理方法，来提高导波雷达物位计的测量准确度。

3.1信号预处理

回波信号中含有高频噪声，需要进行滤波预处理。去除高频噪声的滤波器有以巴特沃斯低通滤波为代表的频域滤波器和以数字平滑算法为代表的时域滤波器，例如：移动平均滤波器［13-14］、中值滤波器等。与频域滤波器相比，时域滤波具有算法简单、运行速度快的优点，因而，特别适合信号的实时处理。为此，选用时域滤波器进行预处理。对于移动平均滤波器，滤波结果是移动窗口内数据加权求和的结果，且所有数据分配了相同的加权因子。不同窗口宽度具有不同的效果：窗口越宽，平滑效果越好，但也会使波形变化率变小，信号幅值降低，信号畸变大，因此，应当合理选择移动窗口宽度。通常选择比半峰宽略小的宽度，由于物位回波的宽度不固定，从10点至20点都存在，因此，对5点、7点、9点移动平均滤波效果进行了对比。

随机选择若干个液位；随机保留各液位下的一组信号，用来计算传播时间。其中，传播时间的计算以传统方法的峰值点为准。对液位-传播时间数据进行最小二乘拟合，并用均方根误差评价其线性度，即作为滤波性能的评价指标。式中：σ为均方根误差；Xi为样本值；为样本均值；n为样本数。计算结果如表1所示。

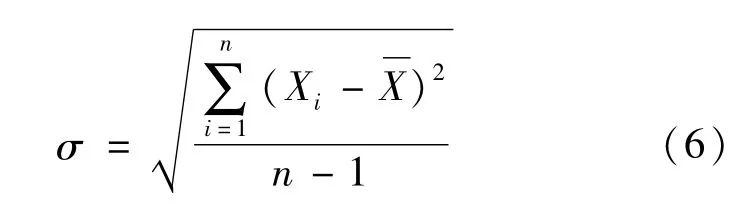
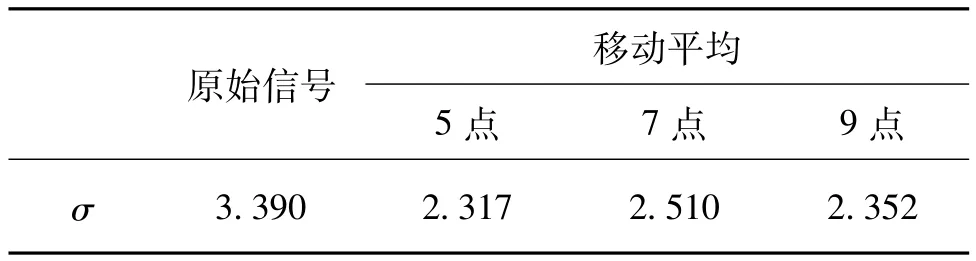
表1　不同窗宽移动平均滤波比较

经过移动平均处理后，均方根误差明显减小；5点移动平均与9点移动平均滤波效果相近，略低于7点移动平均。此外，考虑到越多点数的移动平均滤波改善平顶峰的效果越好，如图3和4所示，将有利于后续特征参数的计算、回波定位点的确定，因此，选择9点移动平均滤波。

3.2物位回波识别

为了避免粗大误差，对物位回波识别方法进行改进，提出基于多特征参数识别的物位回波处理方法，利用回波的多个参数，通过不同方式的结合构成多个判断条件，增强了回波判断的可靠性。

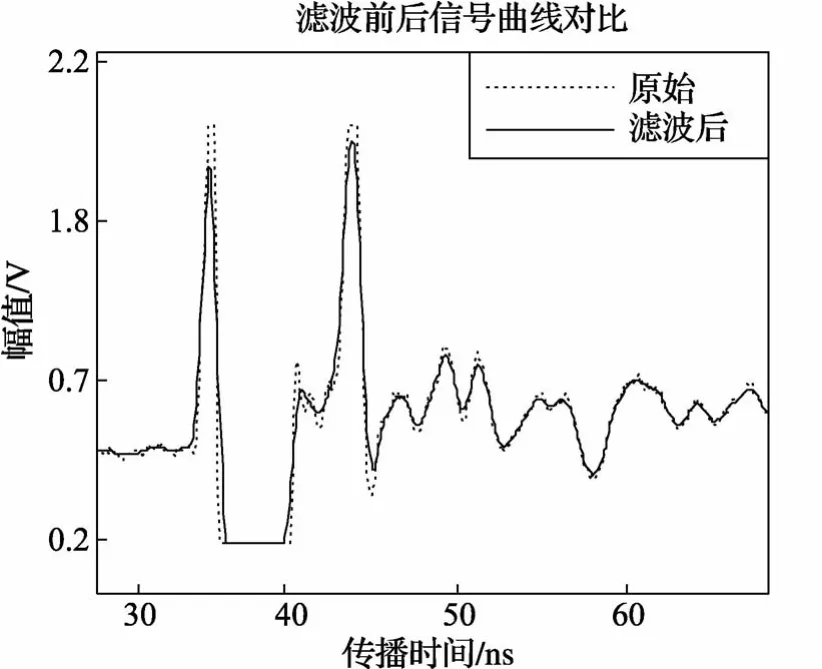
图3　9点移动平均滤波效果

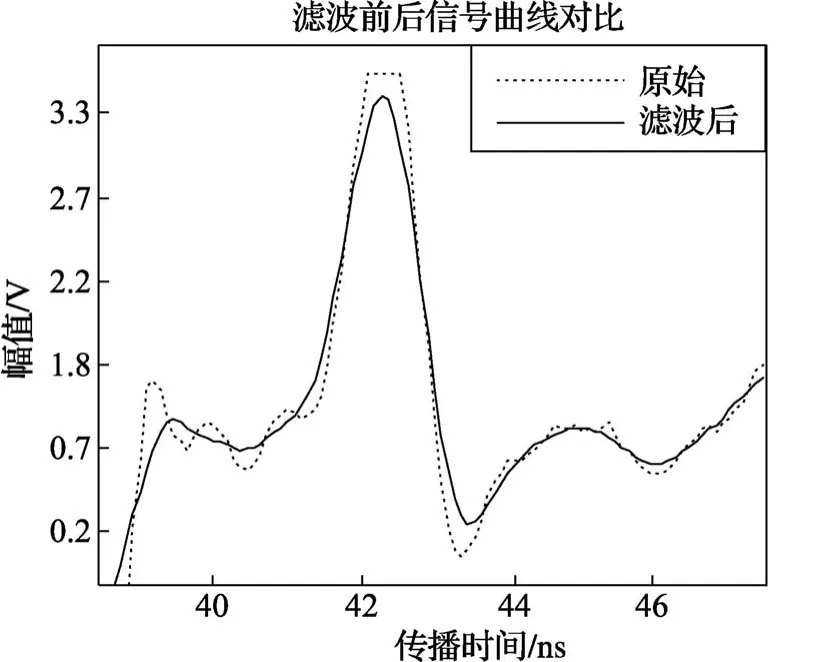
图4　平顶峰滤波后效果

基于在实验室条件下采集的数据，对表征回波特征的参数进行统计分析，包括峰值点幅值、宽度、变化率等，结果表明，多数情况下物位回波具有最大幅值，宽度基本稳定，但回波叠加会导致宽度变大；变化率较大，但随时间没有呈现规律性变化。不同干扰回波有不同特点，难以通过单一条件来确定物位回波。为此，根据干扰回波的特点将其分类，构成不同条件进行排除。

在回波判断时，第一步是通过设置回波宽度、变化率、下降比的下限来排除具有一个或多个参数与物位回波明显不同的虚假回波。这些回波称之为第一类回波，如电子干扰产生的随机窄尖峰脉冲、传感器本身结构反射回波和宽度幅值很小的噪声。第二步再采用综合多个特征参数计算置信度的方法予以排除一个或多个特征参数和物位回波较为接近的干扰波，如二次或多次回波、干扰物产生的回波及宽度较大的噪声。对特征与真实回波接近的干扰波特性进行统计分析可知：宽度越小、峰值点幅值越大，变化率越大的回波为物位回波的可能性越大。因此，根据变化率、峰值点幅值、宽度来设置一个置信度来确定真实回波，其经验公式为：置信度=0.6×变化率+0.1×峰值点幅值-0.3×宽度。其中的0.6、0.1和0.3是权值，可以根据实际情况进行调整。

该方法可以排除虚假回波，准确判断幅值较小的物位回波，分别以不同液位（15 cm和76 cm）的水的回波信号为例，说明该方法的有效性，如图5和6所示。图中，一组△和○对应一个经过去除第一类回波后的剩余回波。其中，△代表起点，○代表结束点；竖直虚线之间标记了经过置信度计算后最终确定的物位回波范围。在图5中，干扰波的特征与回波明显不同，通过判断回波宽度、变化率和下降比等特征就能将其排除，确定出真实物位回波。在图6中，经过第一步判断，可以找到3个波，即图中箭头所指的物位回波和两个干扰回波。其中，第一个干扰回波比物位回波幅值略高，变化率小，宽度大；第二个干扰回波比物位回波幅值低，变化率小，宽度大。将这3个波的特征参数（幅值、变化率、宽度）代入上述经验公式计算各自置信度，物位回波的置信度最大，从而确定其为真实回波。

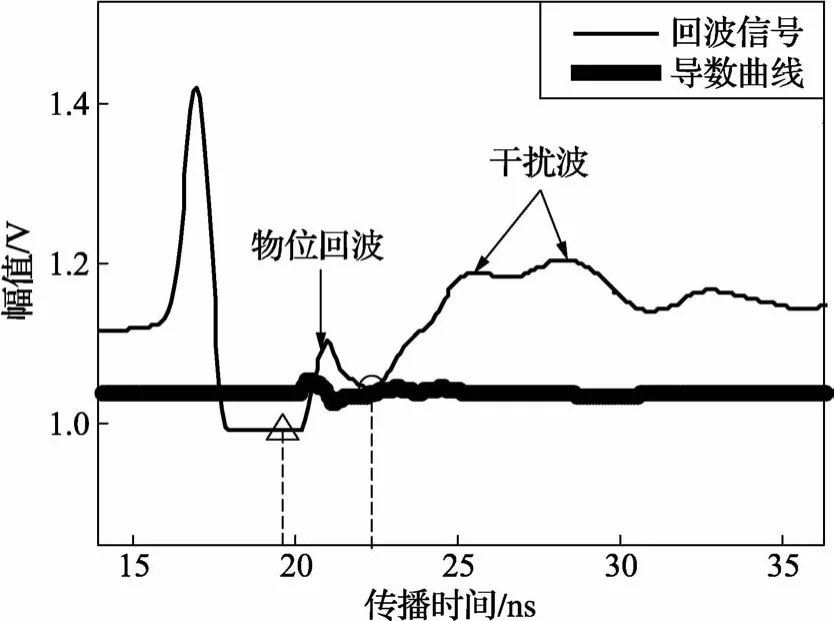
图5　15 cm水位回波信号

3.3回波定位点选择

经过研究，回波的特征点有峰值点、起点、终点、最大斜率点、最小斜率点等，其中，起点和终点往往变动较大，已经不能真实反映回波随液位变化情况，可不考虑。

在实验室条件下，选用5种回波定位点进行比较，分别是：峰值点［15］、经2阶Lagrange插值的峰值点、最大斜率点、最小斜率点，以及以这两点作为边界的区域中心点进行了比较。中心点计算公式为：

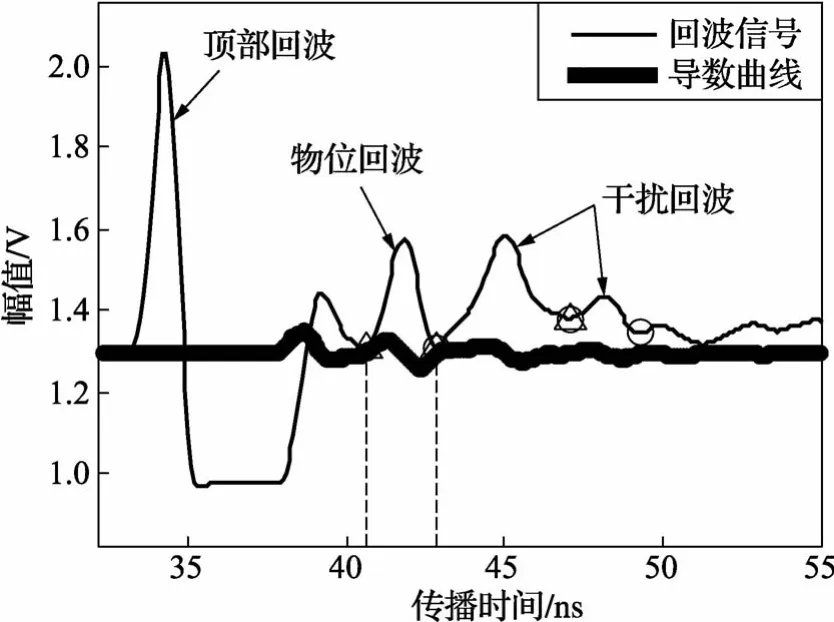
图6　76 cm水位回波信号

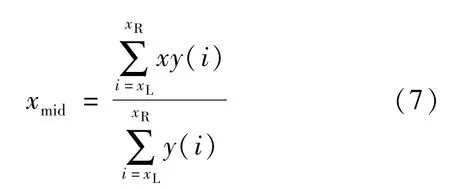
式中：xmid为区域中心点横坐标；xL为左边界点；xR为右边界点；y为回波曲线；x为横坐标。

先对20～100 cm液位范围内随机抽取了27个液位，并在各个液位分别采集一组信号，对信号进行9点移动平均滤波预处理后，分别用峰值点、峰值点2阶Lagrange插值点、最大斜率点、最小斜率点、中心点作为回波定位点，以各回波定位点确定的（物位-时间）线性模型均方根误差作为衡量指标，如表2所示。

表2　不同回波定位点比较

由表2数据可知，用最小斜率点作为回波定位点进行最小二乘拟合的均方根误差最小，即线性度最好，用于计算物位的准确度最高。

3.4计算结果后处理

在实际工作现场中，由于各种干扰的存在，即使物位恒定，传播时间计算值仍不断变化。在同一液位，连续采集5 000组的传播时间计算值，如图7所示。可得传播时间的波动区间为［233.441 9，234.605 9］，最大偏差为1.164 0 ns，对应换算成距离为1.560 9 cm，即同一物位测量值的最大偏差为1.560 9 cm。

根据概率密度的计算方法，将该液位下传播时间的样本波动区间分为30段，对样本进行排序后计算在区间上的概率密度，如图8所示。

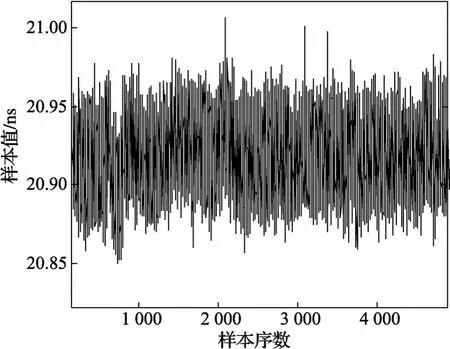
图7　传播时间样本序列

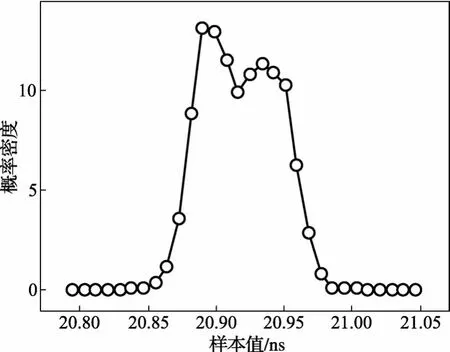
图8　传播时间样本概率密度函数

由图8可知，传播时间样本的概率密度函数不满足高斯分布。故对传播时间采用平均值滤波的方法不能有效减小噪声。为此，选择中值滤波［16］。对传播时间的样本序列进行中值滤波后再计算概率密度函数，并对其进行高斯拟合，其结果见图9。

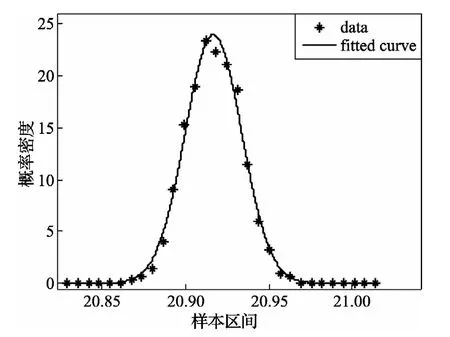
图9　传播时间样本概率密度函数高斯拟合

由图9可看出，经中值滤波后的样本概率密度符合高斯分布，将滤波后的样本再进行平均滤波，可以有效减小随机误差。随机选择30组液位记录液位和对应传播时间计算值，所得数据通过最小二乘拟合确定均方根误差，如表3所示。通过对比表2和表3可知，进行两级滤波有助于减小误差，提高计算准确度。

表3　两级滤波后物位-传播时间模型的均方根误差

4　实验验证

为了验证本文所提方法的有效性，在实验室进行了水位测量实验。导波杆长103 cm，采样频率为50 kHz。分别以峰值点的2阶Lagrange插值点和最小斜率点作为回波定位点进行对比实验。为了考核的严格性，选取能够反映最大测量误差的部分测量结果，如表4所示。

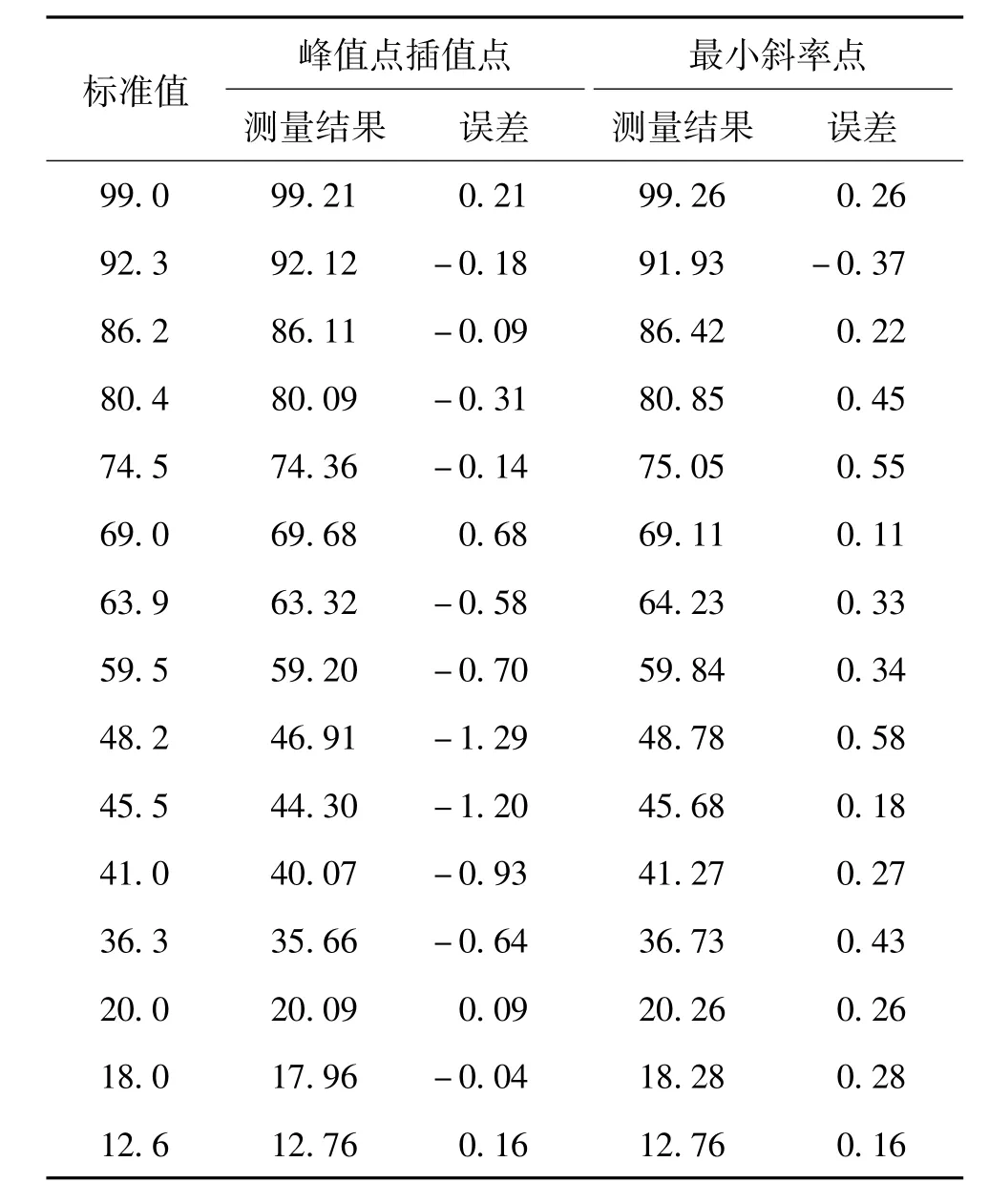
表4　测量结果比较cm

可见，以峰值点的2阶Lagrange插值点为回波定位点的测量误差大于1 cm，以最小斜率点为回波定位点的测量误差在1 cm以内，与理论误差相比均有较大减小。

5　结 论

为了提高导波雷达物位计测量准确度，从硬件和软件两方面对其误差来源进行分析，在信号处理方法上对影响准确度的因素进行修正。

（1）在硬件方面，发射脉冲宽度大、等效时间采样电路的时间间隔大、单片机的采样频率低是导致导波式雷达物位计测量准确度不高的原因。需要改进硬件平台，如减小发射脉冲宽度、提高采样频率、减小等效时间采样电路的时间间隔等，以提高测量的准确度。

（2）在信号处理过程中，仅根据最大峰值来判断有效回波信号是造成导波雷达物位计测量不可靠、测量盲区大的主要原因之一。为此，基于现有硬件条件的限制，提出结合回波特征参数，构成多个条件来排除虚假回波、确定物位回波的方法，提高物位回波判断的可靠性，有效地排除干扰，减小粗大误差。

（3）针对不可避免的噪声干扰导致信号抖动、毛刺现象等，提出采用9点移动平均滤波对信号进行预处理，以及将最小斜率点作为回波定位点进行传播时间计算；针对计算值的波动问题，根据其不符合高斯分布的特点，提出采用中位值平均滤波减小随机误差。实验结果表明，在理论误差为2～4 cm的情况下，实际测量误差小于1 cm，有效地提高了测量准确度。

［1］ Cataldo A，Tarricone L，Attivissimo F，et al.A TDR method for real-time monitoring of liquids［J］.IEEE Trans Instrum Meas，2007，56（5）：1616-1625.

［2］ 张宁，黄杨，李建双.关于物位计测量方法的研究［J］.计量学报，2008，29（z1）：104-106.

［3］ 张宁，黄杨.关于雷达物位计实际应用及其测量方法的探讨［J］.计量学报，2009，30（z1）：111-114.

［4］ 罗斯蒙特储罐雷达股份公司.通过多模式传播的具有介电常数补偿的导波雷达物位计系统：中国，CN201120366374.7［P］.2012-06-06.

［5］ Wall G D.Method for an entropy filter echo processing in time-of-flightorlevelmeasurementsystems：U.S，6935177B2［P］.2005.

［6］ Delin H，Edvardsson O.System and method for filling level determination：U.S，7525476 B1［P］.2009.

［7］ 兰茂亮，赵辉，刘伟佳.导波雷达液位回波信号处理电路的设计［J］.计量技术，2010，（10）：14-17.

［8］ 张龙浩，祝怀标，谯艳.CPLD和MSP430单片机在导波雷达物位计中的应用［J］.电子设计工程，2012，（21）：141-144.

［9］ 刘伟佳，赵辉，唐美芹.一种导波雷达液位计的设计与实现［J］.自动化与仪表，2009，（11）：14-17.

［10］ 姜波，阴丽娟，陈祥光，等.等效时间采样在雷达液位仪中的应用［J］.仪表技术与传感器，2005，（6）：50-54.

［11］ 赵建文，侯媛彬.信号距离度模型及其波形复杂信号辨识［J］.电子测量与仪器学报，2013，27（6）：485-491.

［12］ 李存龙，陈伟民，章鹏.正弦调制型微波测距系统的不确定度分析［J］.仪器仪表学报，2014，35（1）：23 -29.

［13］ 王颖，金志军.常用数字滤波算法［J］.中国计量，2012，（3）：99-100.

［14］ 李聚刚.雷达物位计的应用研究及算法改进［D］.上海：上海交通大学，2008.

［15］ 马远，魏萌，徐科军.基于反向回波的导波雷达物位计信号处理方法［J］.化工自动化及仪表，2013，（12）：1473-1476.

［16］ 李建安，杨学志，高隽，等.两类自适应非线性滤波器设计方法研究［J］.仪器仪表学报，2005，26（8）：374-377.

Measurement Error Analysis and Software Correction of Guided Wave Radar Level Gauge

LIU Zheng， WEI Meng， XU Ke-Jun
（School of Electrical and Automation Engineering，Hefei University of Technology，Hefei，Anhui 230009，China）

The causes of the error of the guided wave radar level gauge（GWRLG）are analyzed，and a software correction method is proposed.The impacts of transmit pulse width and equivalent time sampling interval are studied in hardware.The gross error，the random error and the systematic error generated in the signal processing are researched in software.Based on the existing hardware platform，a set of signal processing method is put forward to reduce the measurement error，i.e.，combining feature parameters to recognize the actual level echo，performing 9 point moving average to preprocess the signal，selecting the minimum slope point as the echo positing point，and conducting median average filtering for the calculated values.The experimental results of water level measurement show that the actual measurement error is reduced to within 1 cm when the theoretical error is 2～4 cm，which validates the effectiveness of the proposed software correction method.

metrology；guided wave radar level gauge；measurement error analysis；software correction

TB938.1

A

1000-1158（2015）05-0506-07

10.3969/j.issn.1000-1158.2015.05.13

2014-08-27；

2015-03-16

刘铮（1990-），男，陕西西安人，合肥工业大学硕士研究生，研究方向为嵌入式系统。292231698@qq.com徐科军为通讯作者。dsplab@hfut.edu.cn