考虑低频振荡的MMC有源阻尼环流抑制方法

徐千鸣　罗　安　马伏军　熊桥坡　王凌志

（1. 湖南大学国家电能变换与控制工程技术研究中心　长沙　410082

2. 国网湖南省电力公司长沙供电公司　长沙　410000）

考虑低频振荡的MMC有源阻尼环流抑制方法

徐千鸣1罗安1马伏军1熊桥坡1王凌志2

（1. 湖南大学国家电能变换与控制工程技术研究中心长沙410082

2. 国网湖南省电力公司长沙供电公司长沙410000）

以直接调制方式的开关函数为出发点，建立MMC每相桥臂电容电压之和与桥臂环流的暂态数学模型，揭示了系统在异常工况下会产生低频振荡环流，推导低频振荡环流的频率，指出无环流控制时，二倍频环流存在谐振点。为实现对低频振荡与二倍频环流的同时抑制，提出一种基于有源阻尼控制的环流抑制方法，简单实用，无需相间解耦与坐标变换。仿真与实验结果表明该方法能同时抑制对暂态时的低频振荡与稳态时的二倍频及以上频次环流，可增强系统稳定性。

模块化多电平低频振荡环流抑制有源阻尼

0　引言

由于具有模块化易扩展、输出电压畸变率低、公共直流母线和无需工频变压器等优点，模块化多电平换流器（Modular Multilevel Converter，MMC）自21世纪初被Rainer Marquardt等提出以来，在高压直流输电、电能质量治理以及中高压变频等领域得到了广泛的应用［1-6］。但MMC在工程应用中也存在子模块电容电压不平衡［7］、环流［8］等问题。

MMC的环流是指在直流母线正负极之间或者不同相之间流动的电流。MMC的分布式储能电容与桥臂电感相串联的特殊结构，使其三相之间以及与外部电网之间容易发生谐振，进而产生低频振荡环流；实际运行中，MMC的子模块电压的波动随调制反映在直流母线电压与输出电压上，导致桥臂电流中存在偶次谐波环流，其中高次谐波环流相比于二倍频环流很小，可以忽略；同时输出电流中含有3次频为主的奇次谐波电流分量，3次及其倍数次谐波电流会被三角形联结的变压器阻断。

现有文献对MMC环流的研究主要集中在二倍频环流产生机理及其抑制方法，对低频振荡环流的机理分析及抑制方法少有报道。文献［9］通过分析二倍频环流的影响因素，指出增大桥臂电抗可以减小二倍频环流，但这不仅增大了换流器成本与损耗，还会降低系统的响应速度；文献［10］通过外加LC滤波电路构成LCL滤波支路，以抑制桥臂的二倍频环流，但引入的LC支路会导致桥臂阻抗存在串联谐振问题；文献［11］建立MMC动态模型，分析了MMC存在的固有低频振荡频率及抑制方法，但没有考虑对二倍频环流的影响；文献［12］详细研究了MMC内部环流和输出电流谐波成分，并给出了二倍频环流的谐振频率；文献［13，14］提出基于坐标变换的二倍频环流抑制方法，但在电网不平衡时需用到多个同步旋转坐标；文献［15，16］提出了无需坐标变换的PI控制和PR控制的环流抑制策略，但增加了控制系统的难度。

针对上述问题，本文根据直接调制方式的开关函数，建立系统桥臂电容电压之和与桥臂环流的数学模型，指出系统低频振荡环流的原因及其频率和二倍频环流谐振问题，提出基于有源阻尼控制的环流抑制方法（Circulating Current Suppressing Method，CCSM），能同时实现低频振荡与二倍频环流的抑制，仿真和实验结果验证了本文提出的控制方法的有效性。

1　MMC环流分析

1.1MMC基本原理

单相MMC结构如图1所示，分为上、下两个桥臂，上、下桥臂相对于直流母线为串联结构，而相对于交流电网是并联结构。每个桥臂均由数目相同或者相近的子模块与一个桥臂电抗串联组成，子模块结构为半H桥。

根据图1，建立电路KVL与KCL方程

图1　MMC单相结构示意图Fig.1　Schematic configuration of single-phase MMC

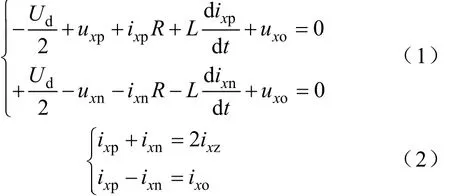
式中，ixz与ixo分别为x（x=a，b，c）相环流与输出电流；Ud为公共直流母线电压；uxp和uxn分别为上、下桥臂的实时投入电压；R、L和C分别为桥臂等效电阻、桥臂电感和子模块电容。

分别将上、下桥臂电压的差模部分与共模部分定义为

联立式（1）～式（3）可得

式（4）包含MMC系统的交流接口微分方程与直流接口微分方程，描述了MMC系统的外部特性与内部特性，可看出MMC输出电流与内部环流之间无耦合。

MMC子模块直流侧并不是理想的直流电源，而是有容值限制的电容。交、直流侧进行功率传输或者相间功率互换时，必然造成电容电压的波动。假设子模块电容电压波动一致，根据桥臂电容电压变化与流过电流的关系，上、下桥臂N个子模块电压之和的波动可以表示为

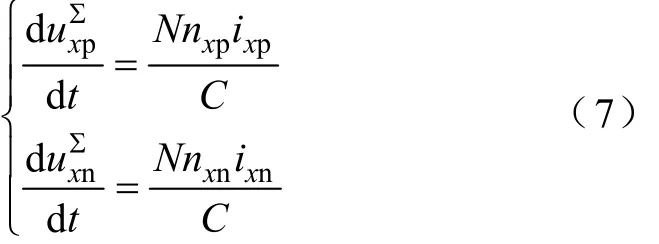
将式（2）、式（3）、式（5）和式（6）代入式（7），可得描述MMC系统上、下桥臂电容电压之和与桥臂环流的三元一阶微分方程组为

为简化分析，对微分方程组进行整理得

将式（9）代入式（8），微分方程组变为

式（10）描述了MMC桥臂电容电压之和及电压之差与环流的关系，设输出参考电压与输出电流为

则换流器单相平均功率P0、脉冲功率P~与瞬时功率P表示为［17］

式中，Uom为输出参考电压幅值；Iom为输出电流幅值；S为换流器单相视在功率；ω0为基波角频率；φ为输出参考电压与输出电流的相位差。

1.2MMC低频振荡环流

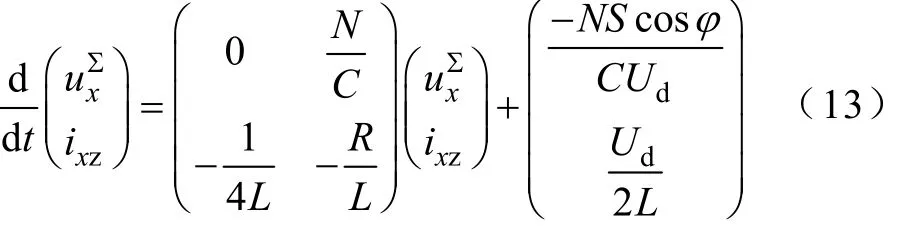
求得系统稳态工作点为

由式（13）的状态矩阵可以解得系统特征方程根为

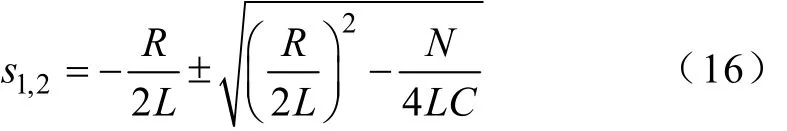
式中，α为振荡的衰减速度；ωlf为振荡的频率，一般低于基波频率，故称之为低频，其数值跟模块个数N、桥臂电抗L、等效电阻R及子模块电容C相关。低频振荡环流的本质是子模块电容经由桥臂电抗及电阻充放电产生的冲击电流。直流侧电压或传输功率的突变都可能导致低频环流的发生，文献［18］针对直流母线短路的工况进行了具体分析，本文不再赘述。

值得注意的是，电感L、电容C及模块数N选择不当时，ωlf可能处于MMC系统典型工作频率如二倍频和四倍频等，使系统发生谐振。进行参数L和C设计时，一般要求ωlf低于基频，忽略桥臂电阻R时，表示为

搭建基于PSIM9.0的三相MMC逆变模型验证推导的振荡环流频率，图2为ωlf与L、C关系三维图，可知ωlf随L和C的减小而增大，当L和C小至一定程度后，ωlf处于工频及以上频次的区域。图3为三电平与五电平模型下，子模块电容保持不变时，ωlf随L变化的曲线，仿真结果和理论分析基本一致，说明理论推导的正确。

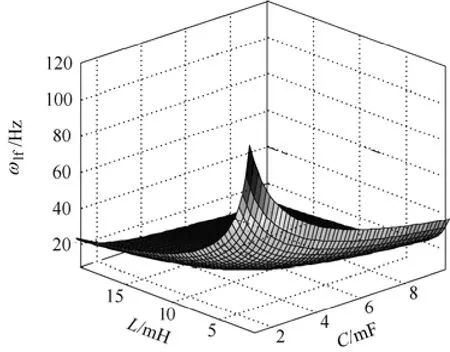
图2　低频振荡频率与桥臂电感、子模块电容关系Fig.2　Relationship between oscillation frequency and arm inductor and sub module capacitance

图3　低频振荡频率与桥臂电感关系Fig.3　Relationship between oscillation frequency and arm inductor

1.3MMC二倍频环流

考虑功率传输导致的二倍频电压与电流波动，将式（11）、式（12）、式（14）和式（15）代入式（10），构造系统小信号模型为

联立式（20）和式（21），二元一阶微分方程组化为一元二阶微分方程

二倍频环流即为微分方程式（22）的特解，解得二倍频环流幅值为［19］

式中

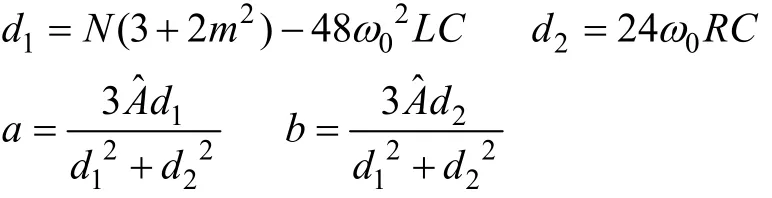
由式（25）可知，当N、L、C满足式（26）时，二倍频环流幅值存在谐振点，其取最大值即式（27），此时二倍频环流幅值完全由桥臂等效电阻R限制。

为避免二倍频环流幅值的谐振放大，参数N、L和C选取需满足约束［20］

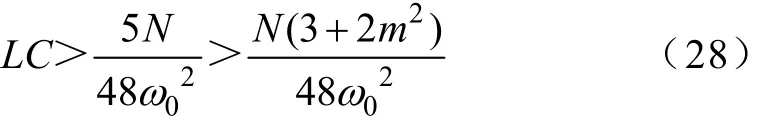
2　MMC环流抑制

由式（16）与式（25）可知，增大系统阻尼比能有效抑制系统在非正常工作状态下的低频振荡环流和二倍频环流。增大系统阻尼比有两种方法［21］：①增大桥臂的等效电阻R，但会导致换流器损耗的增加和效率的降低；②采用有源阻尼控制，通过控制算法增加系统虚拟电阻，在不增加损耗的情况下，增大系统阻尼比，即

式中，环流中交流分量的获得需要先提取环流的直流分量，如何获得桥臂环流中的直流分量成为有源阻尼环流抑制方法控制实现的关键。通常直流分量使用低通滤波器来获取，但低通滤波器存在频带窄的缺点，滤除交流分量的同时，会影响系统动态性能，根据式（21），采用陷波器，将陷波角频率设计为基波频率的2倍，即可获得环流中的直流分量，避免了对陷波频率以外频次的影响，所设计控制策略如图4所示。

图4　有源阻尼环流抑制方法框图Fig.4　Schematic of the proposed CCSM based on active damping control

2.1低频振荡抑制

根据上节所述有源阻尼环流抑制方法，联立式（10）、式（14）和式（15），忽略引入的基频及以上频次波动与高阶部分，重构系统小信号模型可得

由状态矩阵可得系统特征方程根为

为保证系统的稳定性，根据劳斯判据

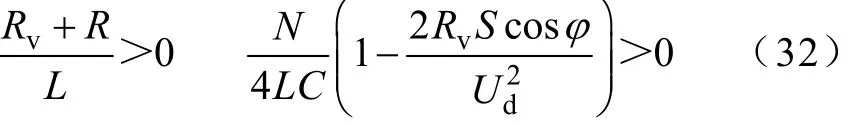
有

由式（33）可知，Rv有很大的取值裕度，使系统为过阻尼状态，即RvȳR，以抑制低频振荡，或在振荡发生时加快其衰减速度，增强系统的稳定性。

图5为加入CCSM前后，系统的伯德图，可以看出加入环流抑制后，谐振峰值明显下降，由L、C引起的低频振荡得到有效抑制。

图5　CCSM加入前后系统伯德图Fig.5　System Bode diagram of MMC with and without CCSM

2.2二倍频环流抑制

由2.1节可知，加入CCSM后，能有效抑制MMC在暂态时的低频振荡。下面进一步研究加入CCSM对稳态时MMC二倍频环流的影响。

加入CCSM后，将式（29）代入式（19），忽略高阶分量，系统可简化为

联立式（20）和式（34），二元一阶微分方程组化为一元二阶微分方程

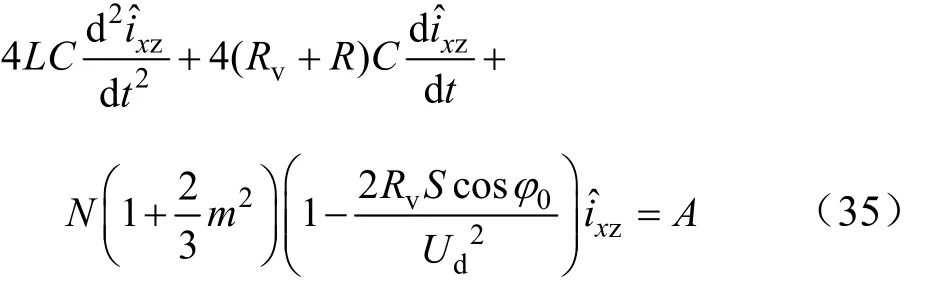
二倍频环流即为式（35）微分方程的特解，解得二倍频环流幅值为

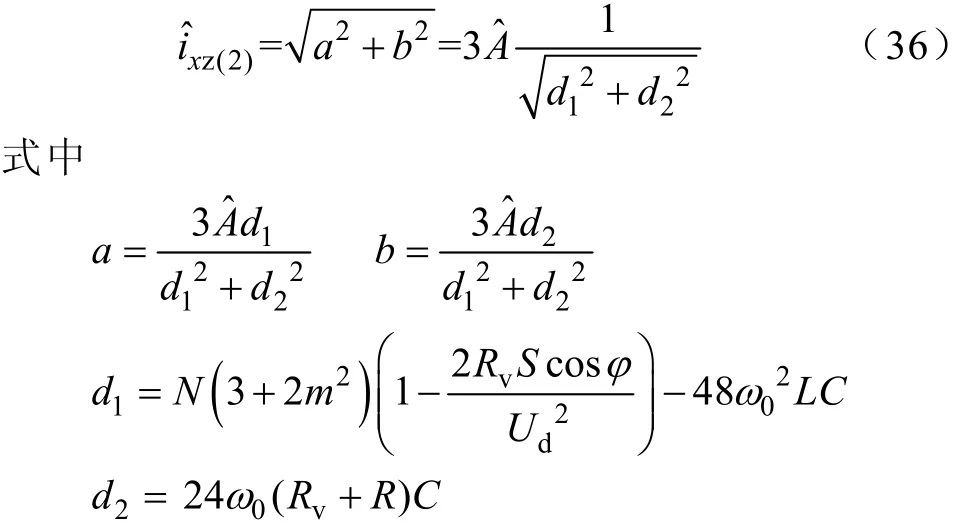
同样，二倍频环流幅值在满足式（37）时，存在谐振点，取得最大值见式（38）。

结合式（25）和式（36），可以看出加入CCSM后，二倍频环流虽没有完全消除，但幅值大幅度减小。

以上分析说明所提出的有源阻尼环流抑制方法不仅可以有效抑制系统暂态时的低频振荡环流，还能有效抑制系统稳态时的二倍频环流。

3　仿真分析

为验证本文提出的有源阻尼环流抑制方法的有效性，在PSIM9.0仿真环境下，搭建了基于图1所示的单相四电平MMC无源逆变模型，Rv取为25Ω，仿真参数见下表。

表　仿真参数Tab.　Simulation parameters

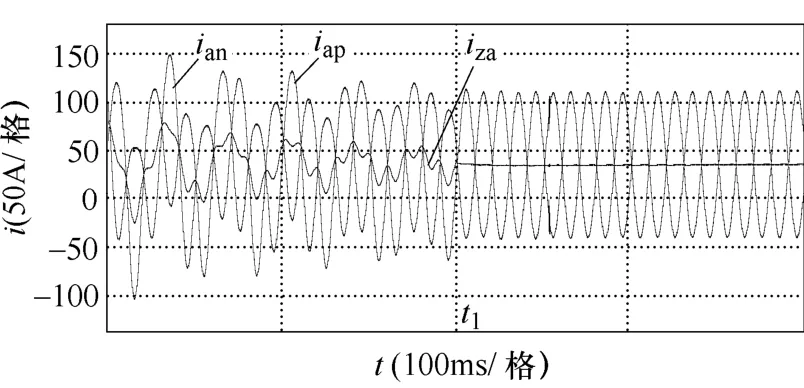
图6　CCSM加入前、后桥臂电流、环流仿真波形Fig.6　Simulation results of arm currents and circulating current

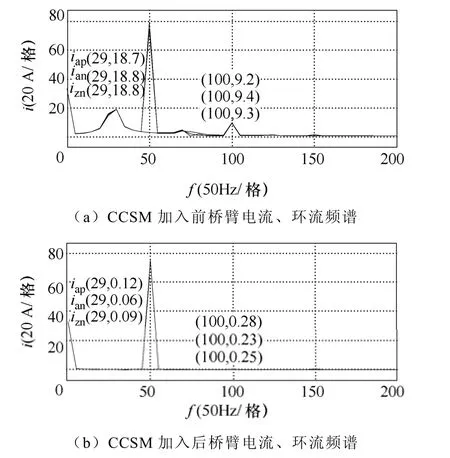
图7　桥臂电流、环流频谱Fig.7　FFT analysis of arm currents and circulating current

t0时刻带载起动MMC，子模块电压开始上升。由图6与图7可知，桥臂环流除含有直流分量外，还存在二倍频分量与29Hz的低频振荡分量。

t1时刻加入有源阻尼环流抑制，低频振荡环流与二倍频环流同时得到抑制，低频振荡环流幅值由18.8A降至0.08A，二倍频环流幅值由9.3A减小为0.25A，而直流分量与基频分量基本不变。表明所提出的有源阻尼环流控制方法能同时有效抑制系统暂态过程中的低频振荡环流与稳态时的二倍频环流，提升系统暂态与稳态性能。

4　实验

为验证本文理论分析及控制策略的效果，在仿真结果正确的基础上，以图1所示的主电路结构为基础，搭建单相四电平MMC样机进行研究，系统设定为滞后无功发生工况，输出参考电压由直流电压外环与无差拍电流内环控制获得，环流抑制策略如图4所示，子模块电容电压平衡采用比例控制，调制方式为载波移相调制。MMC交流侧通过交流调压器与电网AB相连接，调压器一次侧与二次侧电压有效值分别410V与190V，指令电流幅值为30A，模块电容电压设定为200V，载波频率为2kHz，虚拟电阻Rv取20Ω，电压、电流方向与图1一致，其余参数与表1仿真参数相同。

单相四电平MMC实验装置见图8a，图8b为稳态时电网电压eAB（调压器一次侧）与MMC输出无功电流io波形，可以看出无功电流滞后于电网电压约90°，有效值为20.47A。图9a为下桥臂电压波形，峰-峰值为600V左右，图9b为下桥臂子模块6电容电压波形，在202V上下波动。

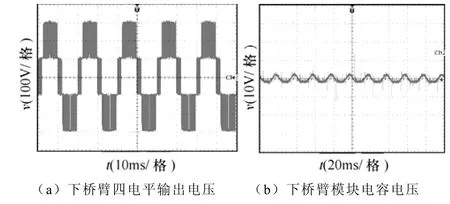
图9　下桥臂电压与模块电容电压波形Fig.9　Waveforms of lower arm voltage and sub module capacitance voltage

在系统已起动后，加入有源阻尼环流抑制，将DSP存储的数据导入到Origin75工作空间，得到环流在CCSM加入前后的波形如图10所示，抑制前存在低频振荡环流与二倍频环流且幅值很大，抑制后不含低频环流，二倍频环流幅值大幅度减小。图11为电能质量分析仪Fluke434记录的环流不控实验与环流控制实验电流波形与频谱的对比。环流不控组：桥臂电流含有较大二倍频分量，电流畸变率（Total Harmonic Distortion,THD）约为15%，输出电流THD为3.4%；环流控制组：二倍频环流大幅度降低，桥臂电流THD降为5%，输出电流THD降至2.6%，说明所述环流抑制方法的有效性。

图10　CCSM加入前后环流波形Fig.10　Waveforms of circulating current

图11　输出电流、桥臂电流波形与频谱Fig.11　Output current，arm currents and spectrum

5　结论

本文建立MMC桥臂电容电压之和与环流的数学模型，得出以下结论：

（1）系统阻尼较小时，暂态过程容易产生低频振荡环流，其频率与主电路参数相关。

（2）无环流控制时，二倍频环流存在谐振点。

（3）基于有源阻尼控制的环流抑制方法能同时对MMC暂态时的低频振荡与稳态时的二倍频及以上频次环流进行抑制。

附录

直流分量在后续计算中，不影响二倍频分量大小，可以省略，其中调制度m=2UomUd，则

对式（A2）中积分项作以下变换

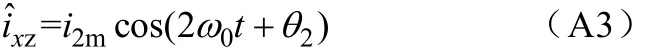
代入式（A2）后，可得

［1］ 汤广福. 基于电压源换流器的高压直流输电技术［M］. 北京： 中国电力出版社，2009.

［2］ Akagi H. Classification，terminology，and application of the modular multilevel cascade converter （MMCC）［J］. IEEE Transactions on Power Electronics，2011，26（11）：3119-3130.

［3］ 邓旭，王东举，沈扬，等. 舟山多端柔性直流输电工程换流站内部暂态过电压［J］. 电力系统保护与控制，2013，41（18）： 111-119.

Deng Xu，Wang Dongju，Shen Yang，et al. Research on transient overvoltage for converter station of Zhoushan multi-terminal VSC-HVDC project［J］. Power System Protection and Control，2013，41（18）：111-119.

［4］ 杨晓峰，范文宝，王晓鹏，等. 基于模块组合多电平变换器的STATCOM及其控制［J］. 电工技术学报，2011，26（8）： 7-13.

Yang Xiaofeng，Fan Wenbao，Wang Xiaopeng，et al. Study on modular multilevel converter based STATCOM and its control［J］. Transactions of China Electrotechnical Society，2011，26（8）： 7-13.

［5］ 翟晓萌，赵成勇，李路遥，等. 模块化多电平动态电压恢复器的研究［J］. 电力系统保护与控制，2013，41（12）： 86-91.

Zhai Xiaomeng，Zhao Chengyong，Li Luyao，et al. Study of modular multilevel dynamic voltage restorer［J］. Power System Protection and Control，2013，41（12）：86-91.

［6］ Baruschka L，Mertens A. A new 3-phase AC/AC modular multilevel converter with six branches in hexagonal configuration［C］. IEEE Energy Conversion Congress and Exposition （ECCE），Phoenix，2011：4005-4012.

［7］ 王奎，郑泽东，李永东，等. 新型模块化多电平变换器电容电压波动规律及抑制方法［J］. 电工技术学报，2011，26（5）： 8-14.

Wang Kui，Zheng Zedong，Li Yongdong，et al. Voltage ripple principle and restrain method of floating capacitors in a new modular multilevel converter［J］. Transactions of China Electrotechnical Society，2011，26（5）： 8-14.

［8］ 杨晓峰，王晓鹏，范文宝，等. 模块组合多电平变换器的环流模型［J］. 电工技术学报，2011，26（5）：21-27.

Yang Xiaofeng，Wang Xiaopeng，Fan Wenbao，et al. Circulating current model of modular multilevel converters［J］. Transactions of China Electrotechnical Society，2011，26（5）： 21-27.

［9］ 屠卿瑞，徐政，郑翔，等. 模块化多电平换流器型直流输电内部环流机理分析［J］. 高电压技术，2010，36（2）： 547-552.Tu Qingrui，Xu Zheng，Zheng Xiang，et al. Mechanism analysis on the circulating current in modular multilevel converter based HVDC［J］. High Voltage Engineering，2010，36（2）： 547-552.

［10］ Ilves K，Norrga S，Harnefors L，et a1. Analysis of arm current harmonics in modular multilevel converters with main-circuit filters［C］. 9th International Multi-Conference on Systems，Signals and Devices（SSD），Chemnitz，2012： 1-6.

［11］ Lennart H，Norrga S，Antonopoulos A，et a1. Dynamic modeling of modular multilevel converters［C］. 14th European Conference on Power Electronic and Applications （EPE），2011： 1-10.

［12］ Ilves K，Antonopoulos A，Norrga S，et a1. Steadystate analysis of interaction between harmonic components of arm and line quantities of modular multilevel converters［J］. IEEE Transactions on Industrial Electronics，2012，27（1）： 57-68.

［13］ 卓谷颖，江道灼，连霄壤. 模块化多电平换流器不平衡环流抑制研究［J］. 电力系统保护与控制，2012，40（24） ： 118-124.

Zhuo Guying，Jiang Daozhuo，Lian Xiaorang. Study of unbalanced circular current suppressing for modular multilevel converter［J］. Power System Protection and Control，2012，40（24）： 118-124.

［14］ Tu Qingrui，Xu Zheng，Zhang Jing. Circulating current suppressing controller in modular multilevel converter［C］. 36th Annual Conference on IEEE Industrial Electronics Society （IECON），2010： 3198-3202.

［15］ 杨晓峰，郑琼林. 基于MMC环流模型的通用环流抑制策略［J］. 中国电机工程学报，2012，32（18）： 59-65.

Yang Xiaofeng，Zheng Qionglin. A novel universal circulating current suppressing strategy based on the MMC circulating current model［J］. Proceedings of the CSEE，2012，32（18）： 59-65.

［16］ Li Zixin，Wang Ping，Chu Zunfang，et a1. An inner current suppressing method for modular multilevel converters［J］. IEEE Transactions on Industrial Electronics，2013，28（11）： 4873-4879.

［17］ Brandon J，Pierquet，David J，et al. A single- phase photovoltaic inverter topology with a seriesconnected energy buffer［J］. IEEE Transactions on Industrial Electronics，2013，28（10）： 4603-4611.

［18］ 王姗姗，周孝信，汤广福，等. 模块化多电平换流器HVDC 直流双极短路子模块过电流分析［J］. 中国电机工程学报，2011，31（1）： 1-7.

Wang Shanshan，Zhou Xiaoxin，Tang Guangfu，et al. Analysis of submodule overcurrent caused by DC pole-to-pole fault in modular multilevel converter HVDC system［J］. Proceedings of the CSEE，2011，31（1）： 1-7.

［19］ 徐政. 柔性直流输电系统［M］. 北京： 机械工业出版社，2012.

［20］ Zhou Yuebin，Jiang Daozhuo，Guo Jie，et al. Analysis and control of modular multilevel converters under unbalanced conditions［J］. IEEE Transactions on Industrial Electronics，2013，28（4）： 1986-1995.

［21］ 张兴，张崇巍. PWM整流器及其控制［M］. 北京：机械工业出版社，2012.

Circulating Current Suppressing Method Based on Active Damping Control of MMC Considering Low-Frequency Oscillation

Xu Qianming1Luo An1Ma Fujun1Xiong Qiaopo1Wang Lingzhi2
（1. National Electric Power Conversion and Control Engineering Technology Research Center Hunan UniversityChangsha410082China
2. State Grid Hunan Electric Power CompanyChangsha410000China）

In order to analyze and suppress the low-frequency circulating currents of modular multilevel converter （MMC），a transient mathematical model for the sum of capacitor voltages and the circulating current of arm is established. The model reveals the principle of low-frequency oscillation under abnormal conditions. And then，the analytical expressions of oscillation frequency and the resonance point of 2nd circulating current without circulating current control are derived. In order to inhibit both low-frequency oscillation and 2nd circulating current，a circulating current suppressing method （CCSM） based on active damping control is proposed，which is simple without decoupling and coordinate transformation. Finally，the simulation and experimental results show that this method can suppress the low-frequency oscillation in transient state as well as 2nd and 2nd above circulating currents in steady state simultaneously.

Modular multilevel converter，low-frequency oscillation，circulating current suppression，active damping

TM712

徐千鸣男，1989年生，博士研究生，研究方向为轻型直流输电与电能质量控制。

罗安男，1957年生，教授，博士生导师，研究方向为电能变换与控制、电能质量控制技术与装备研制。

国家自然科学基金重点项目（51237003）和国家自然科学基金面上项目（51477045）资助。

2014-03-05改稿日期 2014-05-09