考虑土拱效应平移挡土墙地震主动土压力分布

张琪昌，鹿 兴，李 栋

（天津大学机械工程学院，天津　300072）

考虑土拱效应平移挡土墙地震主动土压力分布

张琪昌，鹿 兴，李 栋

（天津大学机械工程学院，天津300072）

基于Mononobe-Okabe理论，考虑土拱效应并假设土拱形状为圆弧形，通过对墙后土体的应力分析推导出在地震作用下土拱形状的曲线方程、侧土压力系数以及水平微分土层间平均剪应力与平均竖向应力二者关系的理论公式.采用水平层分析法推导出平移模式下挡土墙地震主动土压力分布、土压力合力以及合力作用点高度的理论公式，并与Mononobe-Okabe理论、前人方法以及试验数据进行对比分析.结果表明：随着地震系数的增大，土拱形状由下凹圆弧变为下凸圆弧，侧土压力系数也呈现增大趋势；计算出的地震土压力合力与Mononobe-Okabe理论计算值相等，但其分布为非线性分布；与现有理论相比，合力作用点高度与试验结果比较吻合.

土拱效应；挡土墙；地震主动土压力；剪应力

挡土墙被广泛应用在土木工程、水利水电和铁道交通等工程建设领域，其土压力计算问题是挡土墙设计的重要内容.近几年，国内外频频发生地震，作为被广泛应用在工程建设领域的挡土墙，其抗震设计显得非常重要.对于作用在挡土墙上的地震土压力问题，国内外大批学者进行了深入的分析研究，其中最具有代表性的成果便是著名的Mononobe-Okabe理论［1-2］，该理论建立在库伦理论的基础上，将地震作用考虑为惯性力，用静力学方法处理动力学的问题，该方法计算简便，被广泛应用于实际工程中.应用此理论可计算出作用在挡土墙上的地震土压力的合力，且土压力分布为线性分布.然而大量的试验［3-4］表明：地震土压力的合力与Mononobe-Okabe理论的计算结果接近，但土压力分布为曲线分布.卡岗首先采用水平层分析法求解挡土墙土压力，计算出了在静力状态下，土压力分布并非均匀分布［5］.王云球［6］利用卡岗的分析方法，推导出地震主动土压力沿墙高分布的非线性公式以及合力作用点高度的公式，与国外试验结果基本一致.刘忠玉等［7］、张永兴等［8］、王立强等［9］将静力条件下求解土压力的方法推广应用至地震作用下的挡土墙，求解出了地震作用下的挡土墙土压力问题.上述学者在计算地震土压力时并未考虑土拱效应的影响，在计算土压力分布的问题中，不论在静力还是动力情况，墙背和填土之间一定存在摩擦，这必将导致主应力发生偏转，所以土拱效应客观存在.卢坤林等［10］、侯建等［11］虽然考虑了土拱效应来求解地震条件下挡土墙土压力，但是仍然采用静力时的侧土压力系数来计算地震土压力，并没有考虑地震力对侧土压力系数的影响，而且在土拱的形成过程中，由于墙土摩擦角和土体内摩擦角的存在导致挡土墙和基底土体对滑楔体有约束作用，作用在水平土层上的竖向应力并非大主应力，所以水平土层间势必存在剪力作用.黄睿等［12］在计算地震土压力时考虑了水平土层间的剪力，对水平层法进行了改进，但是计算时需要迭代，计算过程复杂.

本文在现有理论的基础上，根据Mononobe-Okabe拟静力学理论，考虑了土拱效应，对挡土墙后填土进行应力分析，应用水平层分析法并且在水平土层间考虑了剪力的作用，从而推导出在地震作用下的侧土压力系数、地震主动土压力求解的理论计算公式，分析了地震系数对计算结果的影响，并和现有方法和试验数据进行比较说明本文的合理性.

1　Mononobe-Okabe理论

根据Mononobe-Okabe理论，当墙后填土面水平、墙体垂直时，地震主动土压力的合力为

式中：γ为土体的重度；H为挡土墙的高度；δ为墙土摩擦角；ϕ为土体内摩擦角；kh为水平地震系数；kv为竖向地震系数；λ为地震角；β为滑裂面倾角.

根据dE/dβ=0可求出地震作用下极限平衡时滑裂面倾角

其中

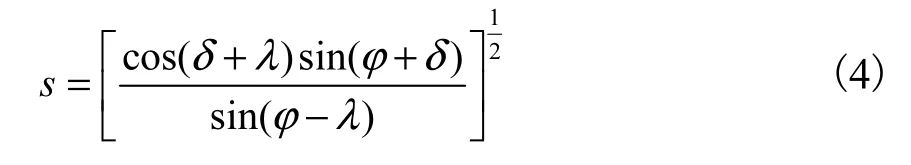
计算时需要满足条件λ＜ϕ，否则式（4）将出现虚数解，此时挡土墙的破坏机理类似于静力状态时的坦墙破坏机理，会在填土中形成第2滑裂面，所以式（4）将不适用.

2　刚性挡土墙后填土应力分析及土拱形状

Terzaghi［13］利用活动门试验证明了土拱效应的存在，在土力学领域中，土拱用来描述应力转移. Handy［14］、Paik等［15］和蒋波等［16］考虑了土拱效应，通过假定不同的土拱形状推导出了静力情况下挡土墙土压力的计算公式.应宏伟等［17］通过对悬链线和圆弧土拱进行计算对比发现差别不大，且由于悬链线土拱形状表达式比较复杂会导致计算不便，建议在实际计算中，可假设土拱形状为圆弧形.本文在Paik等［15］和应宏伟等［17］提出的土拱形状的基础上进行研究，假设墙后小主应力拱为圆弧形.

如图1所示，由于墙土之间存在摩擦，墙背G点处的主应力方向会发生偏转，所以作用在G点处的水平方向应力并非是小主应力，水平土层上每一点的小主应力迹线即为小主应力拱，也就是土拱.

图1　θ1＜θ2时小主应力拱形状Fig.1 Arch of minor principal stress for θ1＜θ2

图2为G点应力状态的摩尔圆，G点处的大主应力与水平方向的夹角1θ计算式［15］为

式中N为大小主应力的比值，即

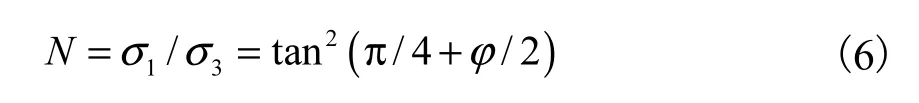
在破裂面上，由极限平衡条件可知大主应力面与

图2　墙土摩擦角部分发挥时的摩尔圆Fig.2 Mohr circle for partially developed wall friction

破裂面夹角α=π/4+ϕ/2，而

许多文献［5，8，10］对滑裂面倾角β与地震系数的关系做了分析，发现地震作用下的滑裂面倾角比静力时的滑裂面倾角小，且随着地震系数的增大，滑裂面倾角呈现出减小的趋势.根据图1和图3可知，土拱的形状可由θ1和θ2的值决定.当θ1＜θ2时，土拱的形状为一条下凹的圆弧曲线，这与在静力状态时的土拱形状类似，如图1所示.由几何关系可知

式中：B为土拱的圆心到挡土墙的水平距离；L为土拱的计算长度，也是土层的长度；x为水平土层上任意一点E到挡土墙的水平距离；ψ为处在圆弧拱任意位置处的半径与水平方向的夹角.由式（8）可得

设圆弧拱曲线的坐标原点为O，在任意深度y0处的圆弧拱曲线的圆心坐标为（B，-Btanθ1+y0），所以圆弧拱曲线方程为

式中0≤x≤L .当地震系数增大时，滑裂面倾角呈现减小的趋势，θ2的值也随之减小，这将导致圆弧形土拱的半径增大，当θ2减小到与θ1相等时，即θ1=θ2时，此时的土拱形状变为一条直线，即在土拱上任意一点的主应力的偏转均和G点相同.随着地震系数继续增大，当θ1＞θ2时，土拱的形状变为下凸的圆弧曲线，如图3所示，图中未知量代表的含义与图1相同.

当θ1＞θ2时，由几何关系可知

经计算，任意深度y0处的圆弧拱曲线方程与式（11）相同，但由于1θ-2θ的值正负不同，所以相同的圆弧曲线方程表示的圆弧土拱的形状不同.

图3　θ1＞θ2时小主应力拱形状Fig.3 Arch of minor principal stress for θ1＞θ2

由摩尔圆理论可知土拱上任意一点E竖向正应力σmv以及剪力mτ计算式分别为：

在G点有

3　侧土压力系数和水平土层间剪应力

考虑土拱效应后，利用水平层分析法求解土压力时，将某一深度处的土层上水平方向应力hσ和作用在水平土层上的竖向应力的平均值σav的比值定义为侧土压力系数，即

由式（17）得

可解得

经计算可得

文献［10-11］虽然考虑了土拱效应，但是在计算时采用的是Handy［14］在计算静力状态的土压力时使用的侧土压力系数，此式对于计算地震作用下的侧土压力系数已经不再适用.实际上，侧土压力系数在地震情况下会随着地震系数的变化而变化，并非一个定值，本文计算出的侧土压力系数考虑了地震系数的影响，所以从理论上说本文结果更加合理.

图4为本文方法计算出的侧土压力系数与地震系数的关系.从图中可以看出，当竖向地震系数kv不变时，侧土压力系数的值随水平地震系数kh的增大呈现出增大的趋势，当水平地震系数kh不为零时，侧土压力系数的值随竖向地震系数kv的增大而增大，此规律可概括为侧土压力系数随地震角λ的增大呈现出增大的趋势.当kh=0时，此时有λ=0，侧土压力系数的值并不随竖向地震系数的变化而变化.特别地，当不考虑地震力时，本文求出的Kw即为静力状态下的侧土压力系数，当不考虑墙土摩擦时，即δ=0时，主应力方向不发生偏转，有θ1=θ2=π/2，此时Kw=1/N，此即为朗肯土压力系数.本文考虑土拱效应得到的侧土压力系数的变化规律与张永兴等［8］研究结果变化规律一致.

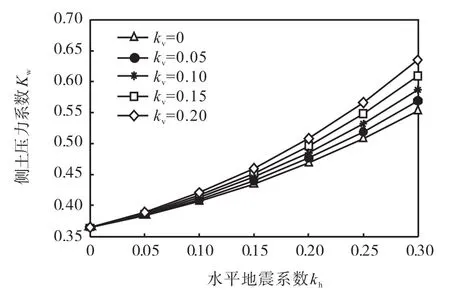
图4　侧土压力系数与地震系数的关系Fig.4 Relation between Kwandkv，kh

图5给出了本文方法和其他方法算出的侧土压力系数的对比，其中取ϕ=30o，δ=20o，kv=kh/3.张永兴等［8］考虑了地震力对侧土压力系数的影响，根据滑楔体力矩平衡条件计算出侧土压力系数，其结果比本文方法计算出的结果大，并且当地震系数较大时，计算出的结果会出现大于1的情况，这不符合主动状态时侧土压力系数的取值.王立强等［9］没有考虑土拱效应，将静止土压力系数代替侧土压力系数，缺乏理论依据.卢坤林等［10］考虑了土拱效应，但是采用的侧土压力系数没有考虑到地震力的作用.虽然侧土压力系数的取值并不会对土压力的合力产生影响，但是会影响到土压力的分布情况，进而对合力作用点的高度产生影响.在对挡土墙进行抗倾覆设计时，合力作用点高度的确定是一项重要内容，所以侧土压力系数的值是否合理，成为设计中的关键问题.

图5　不同方法得到的Kw对比Fig.5 Comparison of Kwamong different methods

目前在计算挡土墙平移模式下土压力问题时，大多数学者都不考虑水平层间的剪力，但是水平层间的剪力是客观存在的.本文按照对水平层间平均竖向应力的计算方法对水平层间的剪应力求平均值，即

可解得

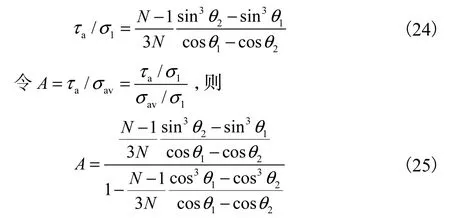
式中A为平均水平剪应力和平均竖向应力的比值.

图6给出了当kv=kh/3，δ/ ϕ取不同值时，A的值随水平地震系数的变化曲线.

从图中可以看出A的值随δ/ ϕ和地震系数的增大呈现出增大的趋势.当地震系数为零且δ/ ϕ＜2/3时，由于A的值很小，即水平层间的剪力与竖向应力的比值很小，在计算挡土墙土压力时可以不考虑剪力.但是当δ/ ϕ比值较大时或者有地震力时，水平层间剪力与竖向应力比值变大，水平层间的剪力不能忽略，在水平层分析中需要考虑剪力的作用.彭述权等［18-19］在计算静力情况挡土墙转动模式下的土压力时将μ 定义为水平层间的摩擦系数.

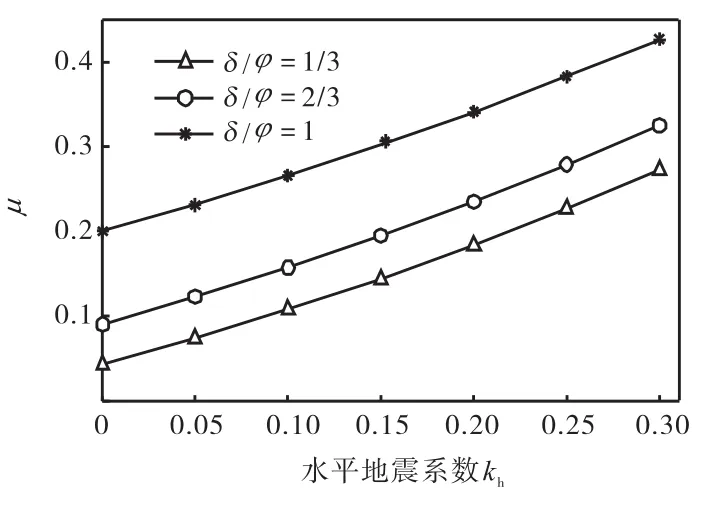
图6　μ 的值与水平地震系数的关系Fig.6 Relation between μ and kh

4　平移模式下挡土墙主动土压力

4.1基本方程

在距滑楔体表面为y处取一厚度为dy的水平土层单元，其受力分析如图7所示.σav和σav+dσav分别为作用于水平土层上下表面的平均竖向应力，Aσav和σav+dσav分别为作用于水平土层上下表面的平均剪应力，σh为挡土墙对水平土层的水平方向反力，τ1为挡土墙与土层之间的摩擦力，r为挡土墙后不动土体对滑楔体在垂直于滑裂面上的反力，τ2为挡土墙后不动土体对滑楔体的摩擦力，dw为水平水层的自重，khdw为水平土层受的水平地震力，kvdw为水平土层受的竖向地震力，β为墙后土体滑裂面与水平方向的夹角.

图7　挡土墙水平土层受力分析Fig.7 Mechanical analysis of the horizontal differential element behind retaining wall

由水平土体微分单元在水平方向上力的平衡条件可得

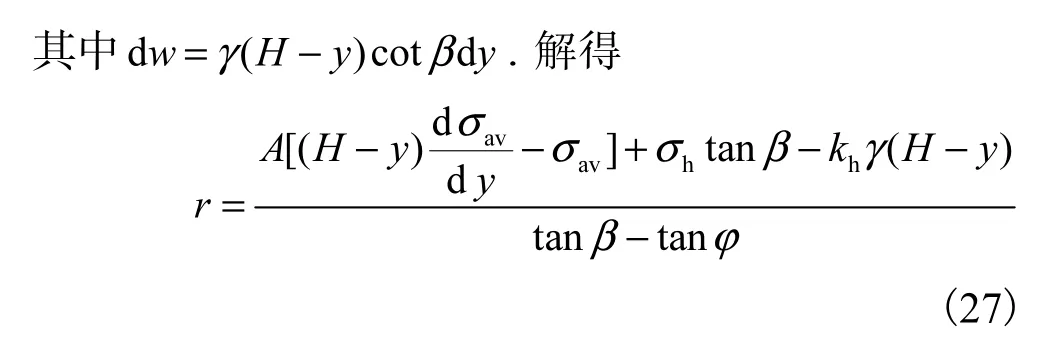
由水平土体微分单元在竖直方向上力的平衡条件可得

解得

令

其中β和Kw的取值由式（3）和（22）求得.

将式（27）、（30）代入式（29），解得

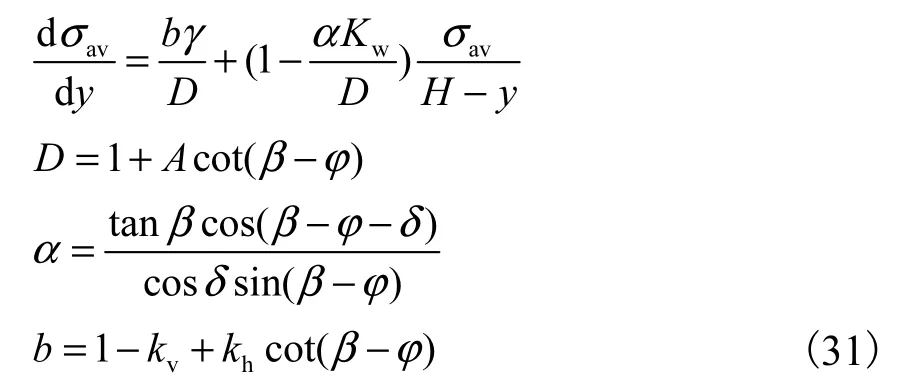
式（31）即为挡土墙平移模式下求解地震主动土压力分布的基本方程.

4.2土压力分布

由边界条件y=0时，q=0可解得

式（33）即为本文推导出的计算挡土墙平移模式下地震主动土压力的理论公式.

图8为在不同的地震系数下，作用在挡土墙上的土压力分布，计算时取ϕ=30o，δ=20o，γ=15.4 kN/m3.由图可知，土压力的分布是非线性的，当竖向地震系数不变时，水平地震系数的增大导致最大土压力值也增大，且出现的位置随之上升，其表现为合力作用点高度的提高.当水平地震系数不变时，随着竖向地震系数的增大，土压力最大值略有减小，当水平地震系数为零时，地震角λ=0，竖向地震系数对土压力分布图形的形状没有影响，只是对土压力值的大小有影响.特别是当水平、竖向地震系数均为零时，式（3）计算出的滑裂面倾角β为库伦滑裂面角度，式（33）中b=1，此时计算出的土压力分布公式即为静力条件下求解主动土压力的计算公式.

图8　不同地震系数下土压力分布Fig.8 Distribution of earth pressure among different kv，kh

图9为不同方法计算出的的土压力分布，在计算时取ϕ=30o，δ=20o，kh=0.20，kv=kh/3，γ=15.4 kN/m3.从图中可以看出Mononobe-Okabe理论得到的土压力分布为线性分布，而其他几种方法计算出的土压力为非线性分布，土压力的变化趋势也基本一致.王立强等［9］未考虑土拱效应，其计算出的土压力最大值的位置较其他方法高，导致合力作用点高度较高.卢坤林等［10］虽然考虑了土拱效应，但是忽略了地震系数对侧土压力系数的影响，其计算出的土压力最大值的位置偏低，导致合力作用点高度偏低，本文计算出的结果位于两者之间.

图9　不同方法土压力分布对比Fig.9Distribution of earth pressure among different methods

4.3土压力的合力及作用点高度

作用在挡土墙上地震主动土压力合力的水平分量为

土压力的合力为

将α和b的表达式代入式（35）中得

将式（2）代入并整理得

式（37）与Mononobe-Okabe理论得到的结果完全相同，所以考虑土拱效应和水平层间的剪力并不会改变土压力合力的大小，但是会使土压力的分布更加合理.特别是当水平、竖向地震系数均为零时，式（37）退化为静力情况下计算土压力合力的库伦理论公式.地震主动土压力对墙底的力矩

土压力合力作用点距墙底的距离

图10为ϕ=30o，δ=20o时，地震主动土压力合力作用点高度随地震系数的变化.从图中可以看出，当kh=0时，无论kv取何值都不会影响合力的作用点高度.当kv一定时，随着kh的增大，合力作用点高度也增大，当kh一定时，合力作用点高度随kv的增大而增大.本文方法计算出的合力作用点高度最小值也位于挡土墙高度的1/3以上，尤其是当地震系数较大时，计算出的合力作用点高度为0.65，H左右，所以如果按照Mononobe-Okabe理论计算出的H/3对挡土墙进行抗倾覆设计会存在较大风险.

图10　地震土压力合力作用点高度随地震系数的变化Fig.10 Change of the height of the point of the resultant force application with kv，kh

图11为本文方法计算出的土压力合力作用点高度与其他方法以及Sherif等［3］试验数据的比较.从图中可以看出，考虑水平层间剪力后，可使计算出的合力作用点高度降低，当kh较小时，两者差别不大可以忽略，但随着kh的增大，两者之间的差别会随之增大，与试验数据相比，考虑水平层间的剪力得到的结果在kh较大时更加接近实测结果，所以考虑水平层间的剪力更为合理.当地震系数较小时，本文方法和考虑了土拱效应的文献［10］方法相差不大，随着kh的增大，文献［10］方法由于没有考虑到地震作用对侧土压力系数的影响，本文计算出的合力作用点高度大于文献［10］方法.对于没有考虑土拱效应的文献［7］方法，本文得到的结果始终小于文献［7］方法结果.

图11　不同方法得出的作用点高度对比Fig.11 Comparison of the height of the point of the resultant force application among different methods

实测数据表明合力作用点高度与地震系数关系不大，当kh较大（kh＞0.3）时，试验结果和理论偏差很大，这是因为现有的方法都是基于水平层分析法求解土压力，所以计算出的合力作用点高度随地震系数的变化呈现出的变化规律相同，均随着地震系数的增大而增大.但是在kh不大（kh＜0.25）时，偏差不大，而且本文方法与实测结果比较吻合.因此本文提出的理论和计算方法较前人理论相比更加准确合理.

5　结 论

（1） 根据对墙后土体应力分析可知土拱的形状与地震系数有关，随着地震系数的增大，土拱形状由下凹形曲线变成下凸形曲线，侧土压力系数增大，水平层间的剪力增大，土拱效应愈加明显.

（2） 本文考虑了地震系数的影响，根据土拱效应计算出侧土压力系数，同时在水平层分析法中考虑了水平层间的剪力作用，使土压力计算模型理论上更加准确，从而推导出土压力分布、土压力合力以及合力作用点高度的计算公式.

（3） 用本文方法得到的地震主动土压力合力与Mononobe-Okabe理论相同，但是土压力呈非线性分布.考虑土拱效应后，合力作用点高度降低，但仍大于墙高的1/3，所以若按Mononobe-Okabe理论计算出的H/3对挡土墙进行抗倾覆设计偏危险.

［1］Okabe S. General theory of earth pressure and seismic stability of retaining wall and dam［J］. Journal of Japanese Society of Civil Engineers，1924，10（5）：1277-1323.

［2］Mononobe N，Matsuo H. On the determination of earthquake pressure during earthquake［C］// Proceedings of Word Engineering Congress. Tokyo，Japan，1929：1277-1778.

［3］Sherif M A，Ishibashi I，Lee C D. Earth pressure against rigid retaining walls［J］. Journal of Geotechnical Engineering，1982，108（5）：679-695.

［4］Sherif M A，Fang Y S. Dynamic earth pressure on walls rotating about top［J］. Soil and Foundations，1984，24（4）：109-117.

［5］顾慰慈. 挡土墙土压力计算［M］. 北京：中国建筑材料工业出版社，2001.

Gu Weici. The Calculation of Earth Pressure of Retaining Walls［M］. Beijing：China Building Materials Industry Press，2001（in Chinese）.

［6］王云球. 地震土压力的非线性分布［J］. 华东水利学院学报，1983（4）：61-72.

Wang Yunqiu. Non-linear distribution of earth pressure during earthquake［J］. Journal of East China Technical University of Water Resources，1983（4）：61-72（in Chinese）.

［7］刘忠玉，杨会朋，何盛东. 刚性挡土墙地震主动土压力的非线性分布［J］. 郑州大学学报，2004，39（2）：36-38.

Liu Zhongyu，Yang Huipeng，He Shengdong. Nonlinear distribution of seismic active earth pressure onrigid retaining walls［J］. Journal of Zhengzhou University，2004，39（2）：36-38（in Chinese）.

［8］张永兴，陈 林. 地震作用下挡土墙主动土压力分布［J］. 深圳大学学报：理工版，2012，29（1）：31-37.

Zhang Yongxing，Chen Lin. Seismic active earth pressure of retaining wall ［J］. Journal of Shenzhen University：Science and Engineering，2012，29（1）：31-37（in Chinese）.

［9］王立强，王元战，迟丽华. 挡土墙地震土压力及其分布［J］. 中国港湾建设，2007，151（5）：1-5.

Wang Liqiang，Wang Yuanzhan，Chi Lihua. Distribution of seismic soil pressure on a retaining wall［J］. China Harbour Engineering，2007，151（5）：1-5（in Chinese）.

［10］卢坤林，杨 扬，朱大勇，等. 考虑土拱效应的挡土墙地震土压力及其分布［J］. 水电能源科学，2010，28（5）：65-68.

Lu Kunlin，Yang Yang，Zhu Dayong，et al. Seismic active earth pressure of retaining wall considering soil arching［J］. Water Resources and Power，2010，28（5）：65-68（in Chinese）.

［11］侯 建，夏唐代，陈炜昀，等. 考虑土拱效应的挡土墙地震主动土压力静力研究［J］. 岩石力学与工程学报，2013，32（增1）：2825-2832.

Hou Jian，Xia Tangdai，Chen Weiyun，et al. Static study of seismic active earth pressure on retaining walls considering soil arching effect［J］. Chinese Journal of Rock Mechanics and Engineering，2013，32 （Suppl1）：2825-2832（in Chinese）.

［12］黄 睿，夏唐代. 无粘性土的地震主动土压力水平层法改进［J］. 哈尔滨工业大学学报，2014，46（2）：85-91.

Huang Rui，Xia Tangdai. Improved horizontal slice method for seismic active earth pressure of cohesionless soil［J］. Journal of Harbin Institute of Technology，2014，46（2）：85-91（in Chinese）.

［13］Terzaghi K. Theoretical Soil Mechanics［M］. New York：Wiley，1943.

［14］Handy R L. The arch in soil arching［J］. Journal of Waterway，Port，Coastal and Ocean Engineering，1985，111（3）：302-318.

［15］Paik K H，Salgado R. Estimation of active earth pressure against rigid retaining walls considering arching effects ［J］. Geotechnique，2003，53（7）：643-653.

［16］蒋 波，应宏伟，谢康和. 挡土墙后土体拱效应分析［J］. 浙江大学学报：工学版，2005，39（1）：131-136.

Jiang Bo，Ying Hongwei，Xie Kanghe. Arching effect behind retaining wall［J］. Journal of Zhejiang University：Engineeing Science 2005，39（1）：131-136（in Chinese）.

［17］应宏伟，蒋 波，谢康和. 考虑土拱效应的挡土墙主动土压力分布［J］. 岩土工程学报，2007，29（5）：717-722.

Ying Hongwei，Jiang Bo，Xie Kanghe. Distribution of active earth pressure against retaining walls considering arching effect［J］. Chinese Journal of Geotechnical Engineering，2007，29（5）：717-722（in Chinese）.

［18］彭述权，周 健，樊 玲，等. 考虑土拱效应刚性挡墙土压力研究［J］. 岩土力学，2008，29（10）：2701-2707.

Peng Shuquan，Zhou Jian，Fan Ling，et al. Research on earth pressure of rigid retaining wall considering soil arching［J］. Rock and Soil Mechanics，2008，29（10）：2701-2707（in Chinese）.

［19］樊 玲，彭述权. 考虑土拱效应绕墙顶转动刚性挡墙土压力分布［J］. 扬州职业大学学报，2006，10（4）：39-44.

Fan Ling，Peng Shuquan. Distribution of earth pressure of retaining wall with wall movement about top considering soil arching［J］. Journal of Yangzhou Polytechnic College，2006，10（4）：39-44（in Chinese）.

（责任编辑：金顺爱，王晓燕）

Distribution of Seismic Active Earth Pressure of Retaining Wallin Translation Mode Considering Soil Arching

Zhang Qichang，Lu Xing，Li Dong
（School of Mechanical Engineering，Tianjin University，Tianjin 300072，China）

Based on Mononobe-Okabe theory，considering arch effect and assuming that soil arching was in the form of circle，after analyzing the stress of the filling behind retaining wall，the equation of soil arching was obtained，as well as the lateral earth pressure coefficient and a theory formula which is to calculate the relationship between the average shear stress and the average vertical stress on the horizontal differential elements.By using the method of horizontal differential element，an improved formula of the distribution of seismic active earth pressure resultant force and its points of application were obtained.The proposed method was compared with the existing methods and experimental data.It shows that the resultant seismic earth pressure is the same as that given by Mononobe-Okabe theory.The distribution of seismic earth pressure is non-linear.With the increase of seismic coefficient，soil arch shape changes，the coefficients of lateral earth pressure also increases.Compared with the existing theory，the heights of points of application of the resultant force of proposed method are in consistence with the results of model test. Keywords：soil arching；retaining wall；seismic active earth pressure；shear stress

TU432

A

0493-2137（2015）12-1063-08

10.11784/tdxbz201410021

2014-10-11；

2014-12-30.

天津应用基础与前沿技术研究基金资助项目（12JCZDJC28000）.

张琪昌（1959—），男，博士，教授，qzhang@tju.edu.cn.

李 栋，dinlog@126.com.

网络出版时间：2015-01-14. 网络出版地址：http://www.cnki.net/kcms/detail/12.1127.N.20150114.1523.001.html.