基于广义流和广义力的河流能耗率推导

赵丽娜，徐国宾

（天津大学水利工程仿真与安全国家重点实验室，天津　300072）

基于广义流和广义力的河流能耗率推导

赵丽娜，徐国宾

（天津大学水利工程仿真与安全国家重点实验室，天津300072）

基于非平衡态热力学理论中局域熵产生和能耗函数的关系，以及能耗函数可以写作不可逆过程中每个广义流与其相应的广义力的乘积之和，构造了河流的广义力和广义流，推导出河流的能耗函数数学表达式.通过对能耗函数做体积分，进而推导出河流的能耗率.从而避开使用众多复杂的非平衡态热力学和高等流体力学公式，过程简便且易于理解.

河流；非平衡态热力学；广义流；广义力；能耗率

河流是个开放的、复杂的动力系统，不仅具有自动调整功能趋向于动力平衡，而且河流内部能量趋向于按照一定规律分配.国内外许多学者曾从能耗率的角度去研究河流水流的运动规律，其中有美籍华裔杨志达和国内徐国宾等学者.Yang等［1-5］利用河流的势能与热力学系统的热能之间的类同，认为河流中唯一有用的能量是它的势能，并进一步假定河流中的势能和高程分别相当于热力学系统中的势能和绝对温度，根据这些概念，提出了单位水流功率，并基于单位水流功率概念，给出了最小能耗率原理数学表达式.徐国宾等［6-9］基于非平衡态热力学的最小熵产生原理，利用流体力学中的连续方程、运动方程和能量方程以及热力学的吉布斯公式，经过严谨的数学推演得到了流体最小能耗率原理数学表达式，进一步完善了最小能耗率理论，同时指出最小能耗率原理等价于最小熵产生原理.

本文将基于非平衡态热力学理论，构造河流的广义流和广义力，推导出河流的能耗函数数学表达式，进而推导出河流的能耗率，从而避开使用众多复杂的非平衡态热力学和高等流体力学公式，使推导过程简便且易于理解.

1　熵流和熵产生的回顾

当系统存在有外力场且其内部存在黏滞性流动时，单位体积中的熵平衡方程［10］为

式中：SV为熵密度，表示单位体积中的熵；t为时间；u为平均流速；jq为热流；T为温度；kμ为单位质量的第k组分的化学势；jk为单位质量的第k组分的物质流；Mk为单位质量的第k组分的分子量；Fk为单位质量的第k组分的质量力；vk，λ为参与第λ个反应的反应物k的化学计量系数.

一个系统的总熵随时间的变化可以写作

式中：S为系统的总熵；V为系统的体积；Ω为系统的表面积；JS代表通过单位面积的熵的交换速率，简称熵流；σ代表单位体积中熵产生的速率，即局域熵产生.

利用Gauss定律，由式（2）可得

比较式（1）和式（3）得到熵流和熵产生的表达式

其中，定义

式（4）和式（5）中的每一项都有明确的物理意义.式（4）右边第1项代表由对流过程引起的熵流，第2项为由热传导引起的熵流，第3项为由扩散过程引起的熵流.

现在来专门研究一下式（5）.式（5）右边的第1项与热传导有关，第2项和扩散过程有关，第3项和黏滞性流动有关，第4项和化学反应有关.值得注意的是式中每一项本身都是由两个因子的乘积组成.其中的一个因子和不可逆过程的速率有关，例如热流jq、扩散流jk、黏性应力张量Π/T和化学反应速率ωλ，这些速率因子可以称为不可逆过程的广义流，简称“流”；式（5）右边各项中的另一个因子和引起相应“流”的推动力有关，例如温度梯度∇（1/T）引起热流，化学势梯度-∇（μk/T）以及外力MkFk/T引起扩散流，流速梯度-∇u引起黏滞性流动，Aλ/T是化学反应的推动力.这些和推动力有关的因子可以广义地称之为不可逆过程的广义力，简称“力”.如果用Jk代表第k种不可逆过程的流，用Xk代表第k种不可逆过程的力，则式（5）可以写作如下一般形式

这就是说，局域熵产生可以写作不可逆过程的广义流和相应广义力的乘积之和的形式.

2　基于广义流和广义力的河流能耗率推导

根据非平衡态热力学，局域熵产生和能耗函数存在下列关系［10］

式中φ为能耗函数.

在实际应用中，可以认为局域熵产生等价于能耗函数，则根据式（7），能耗函数也可以表示为

需要注意的是，构造能耗函数的广义流和广义力的原则和构造熵产生的广义流和广义力的原则一样，只不过构造能耗函数的广义流和广义力时，需要两者的乘积具有能耗函数的量纲［ML-1，T-3］，其中M、L及T分别代表质量、长度及时间.

一旦合理地确定了广义力和广义流之后，便可以由式（9）定量地计算由不可逆过程引起的能耗函数.

2.1河流的广义力和广义流的选择

河流中存在两种流，即物质流和能量流［11］.在不考虑热交换的情况下，能量流是通过动量传输实现的，物质流是通过扩散完成的.

众所周知，单位体积的流体所具有的动量为uρ，将通过给定流体空间边界面的流体动量通量定义为动量流，则动量流等于流体的动量uρ和质量中心速度u的乘积［11］，即

式中ρ是水流密度.

流速梯度的存在将发生动量扩散，这类扩散由高速区指向低速区，于是动量流对应的广义力是沿着流向的梯度［10］，即

式中l为流向的坐标轴.

对于质量流，定义为密度乘以速度，即单位时间内扩散的质量［11］

在河流中对应于水流流动的驱动因子是重力.重力在l方向的分量为质量流对应的广义力［11］，即

式中：g为重力加速度；i表示水面比降［12］，，对于平原河流，i的值很小时（i≤6°）sini=i［12］，于是得到

2.2量纲分析

在国际单位制中，对于力学问题，采用的3个基本量纲分别是长度、时间和质量，即L、T、M制，广义力和广义流乘积的量纲都可以由长度、时间和质量的量纲导出［12］.河流的动量流和动量力的乘积为，其量纲为河流的质量流和质量力的乘积为JmXm=ρu· gi，其量纲为，可以看出本文构造的河流的广义力和广义流的乘积具有能耗函数的量纲.

2.3河流的能耗函数

根据式（9）可知，河流的能耗函数可以表示为

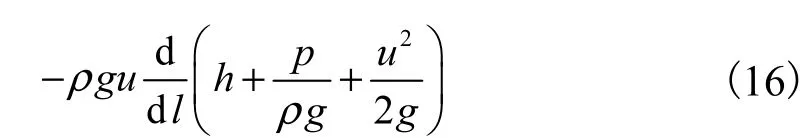
河流的水力比降［12］，则式（16）变为

式中：γ为水容重；J为水力比降.

对能耗函数求体积分，得到流体的能耗率的表达式为

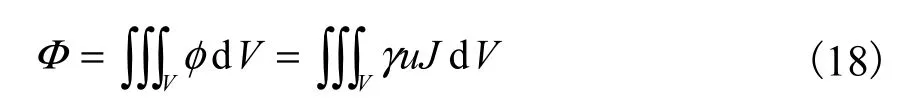
沿水流方向取单位长度l=1，并且设在单位长度内J是常数，则式（18）简化为

式中：A为过流断面；Q为流量.

设式（19）中，过水断面为常数，所以式（19）可以简化为Φ=uJ.为了实用起见，对于大多数的天然河流，可以用水面比降i取代水力比降J［13］，因此杨志达定义的单位水流功率ui是式（19）的简化和实用形式.

3　结 语

本文基于非平衡态热力学理论，能耗函数等于每个广义流与其相应的广义力的乘积之和，构造了河流的广义力和广义流，进而推导得出河流能耗率表达式，该表达式与杨志达和徐国宾推导得出的能耗率形式一样，但推导过程简便且易于理解，从另一个角度再次证明了河流的能耗率公式的确是Φ=γQJ .

［1］Yang C T. Potential energy and stream morphology ［J］. Water Resources Research，1971，7（2）：311-322.

［2］Yang C T. Unit stream power and sediment transport ［J］. Journal of the Hydraulics Division，ASCE，1972，98：1805-1826.

［3］Yang C T. Minimum unit stream power and fluvial hydraulics ［J］. Journal of the Hydraulics Division，ASCE，1976，102（7）：919-934.

［4］Yang C T，Song C C S. Theory of minimum rate of energy dissipation ［J］. Journal of the Hydraulics Division，ASCE，1979，105：769-784.

［5］Yang C T，Song C C S. Theory of Minimum Energy andEnergy Dissipation Rate ［M］. Houston：Gulf Publishing Company，1986.

［6］徐国宾，杨志达. 基于最小熵产生与耗散结构和混沌理论的河床演变分析［J］. 水利学报，2012，43（8）：948-956.

Xu Guobin，Yang C T. Analysis of river bed changes based on the theories of minimum entropy production dissipative structure and chaos ［J］. Journal of Hydraulic Engineering，2012，43（8）：948-956（in Chinese）.

［7］徐国宾，练继建. 流体最小熵产生原理与最小能耗率原理（Ⅰ）［J］. 水利学报，2003（5）：35-40.

Xu Guobin，Lian Jijian. Theories of the minimum rate of energy dissipation and the minimum entropy production of flow（Ⅰ）［J］. Journal of Hydraulic Engineering，2003（5）：35-40（in Chinese）.

［8］徐国宾，练继建. 流体最小熵产生原理与最小能耗率原理（Ⅱ）［J］. 水利学报，2003（6）：43-47.

Xu Guobin，Lian Jijian. Theories of the minimum rate of energy dissipation and the minimum entropy production of flow（Ⅱ）［J］. Journal of Hydraulic Engineering，2003（6）：43-47（in Chinese）.

［9］徐国宾，练继建. 河流调整中的熵、熵产生和能耗率的变化［J］. 水科学进展，2004，15（1）：1-5.

Xu Guobin，Lian Jijian. Changes of the entropy production and the rate of energy dissipation in river adjustment［J］. Advances in Water Science，2004，15（1）：1-5（in Chinese）.

［10］李如生. 非平衡态热力学和耗散结构［M］. 北京：清华大学出版社，1986.

Li Rusheng. Non-Equilibrium Thermodynamics and Dissipative Structures［M］. Beijing：Tsinghua University Press，1986（in Chinese）.

［11］王 铮. 利用耗散结构理论分析河道演变［J］. 地理科学，1989，9（2）：173-180.

Wang Zheng. Analysis of river channel change with theory of dissipative structure ［J］. Scientia Geographica Sinica，1989，9（2）：173-180（in Chinese）.

［12］李家星，赵振兴. 水力学［M］. 南京：河海大学出版社，2005. Li Jiaxing，Zhao Zhenxing. Hydraulics ［M］. Nanjing：Hohai University Press，2005（in Chinese）.

［13］Yang C T. Formation of riffles and pools ［J］. Water Resources Research，1971，7（6）：1567-1574.

（责任编辑：樊素英）

Derivation of Energy Dissipation Rate of River Based on Generalized Flux and Generalized Force

Zhao Lina，Xu Guobin
（State Key Laboratory of Hydraulic Engineering Simulation and Safety，Tianjin University，Tianjin 300072，China）

Based on non-equilibrium thermodynamics，local entropy production is a function of energy dissipation function，and the latter can be written as the sum of the product of the generalized forces and the corresponding generalized flux of an irreversible process.In this way，once the generalized forces and the corresponding generalized flux of river are formed，the formula of energy dissipation function of river can be obtained.Energy dissipation rate of river system is obtained by volume integral for energy dissipation function.In the entire derivation，the use of many complex equations of non-equilibrium thermodynamics and advanced fluid mechanics can be avoided，making it simple and easy to understand.

river；non-equilibrium thermodynamics；generalized flux；generalized force；energy dissipation rate

TV147

A

0493-2137（2015）12-1126-04

10.11784/tdxbz201406020

2014-06-08；

2015-04-10.

国家自然科学基金创新研究群体科学基金资助项目（51321065）；国家自然科学基金资助项目（50679053）.

赵丽娜（1983—），女，博士研究生，neimengguzhaolina@163.com.

徐国宾，xuguob@sina.com.