上市公司财务预警的T逻辑回归模型

徐　征，刘遵雄

（1.华东交通大学电气学院，江西，南昌　330013；2.华东交通大学信息工程学院，江西，南昌　330013）

上市公司财务预警的T逻辑回归模型

*徐征1，刘遵雄2

（1.华东交通大学电气学院，江西，南昌330013；2.华东交通大学信息工程学院，江西，南昌330013）

针对经典的逻辑回归模型易受到样本类别噪声干扰的问题，采用T逻辑回归算法中的非凸损失函数以弥补这一不足。对T逻辑回归模型及求解算法进行了分析，建立T逻辑回归财务预警模型，并结合沪深上市公司财务数据开展实证分析，结果表明T逻辑回归模型具有较好的分类效果和鲁棒性。

财务危机预警；正则化技术；T-逻辑回归；过拟合；非凸损失函数

0　引言

随着我国证券市场的迅速发展，上市公司的质量会影响资本市场的健康发展。财务危机预警可以提前揭示风险，以便采取有效措施，防范和化解危机［1-3］。上市公司财务预警是通过研究和分析财务状况指标反映上市公司财务经营的相关数据，构建金融危机预警模型。由于财务预警指标变量多、相关性大，不利于建模分析，所以通常需要进行变量选择，然后对独立变量选择模型进行训练，利用统计学习的稀疏矩阵建模，并对上市公司的财务预警进行分析，从而提高模型的解释和预测精度。

经典的逻辑回归对变量的分布没有要求并且预报精度高、解释能力强［4］，但是与多元线性回归模型一样存在过拟合的问题，需要通过统计学习理论中的正则化技术来解决［5］。优化凸性函数能保证正则化风险最小化问题收敛到全局最优，但是凸损失函数的学习算法对噪音不具备鲁棒性，因此需要引入非凸损失函数来弥补凸损失函数的不足。

本文将t指数族中的学生分布引入逻辑回归，对应的正则化风险最小化问题的损失函数具有非凸性。但是这也导致了正则化优化的风险［6］。因此将目标函数对数化，采用凸多乘积规划，对目标跟随函数最小化求解参数。T逻辑回归能较好处理类别噪音，具有优越的性能。

1　T逻辑回归理论

T逻辑回归规定p（ y x，θ）服从条件t指数族［9］分布，

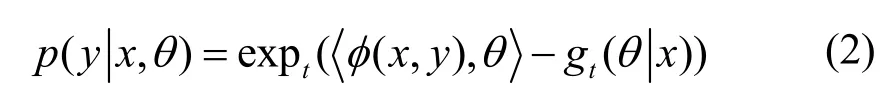
其中1＜t ＜2。

学生分布［10-12］可以看作t指数族分布中相对于正态分布先验的形式，一维学生分布定义为：

其中Γ（·）为伽马函数，v＞1，其均值为有限值。选择t使之满足-（v +1）/2= 1/（1-t ），令

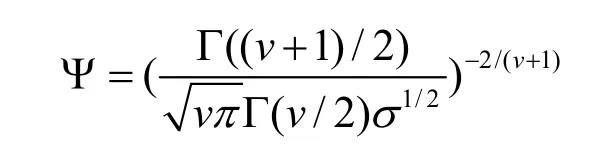
则有：

假定θ先验概率服从学生分布，则

当用学生t指数先验，logp（θ）-不再是凸的，但这也导致存在优化正则化风险挑战。由于t对数函数logt相对于log，是一个单调递增函数，因此可以利用logt函数。

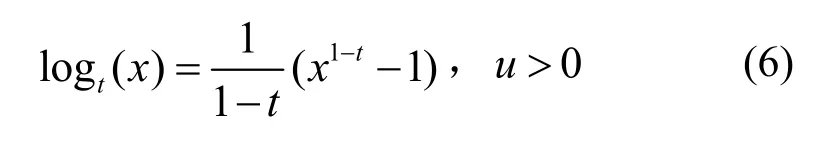
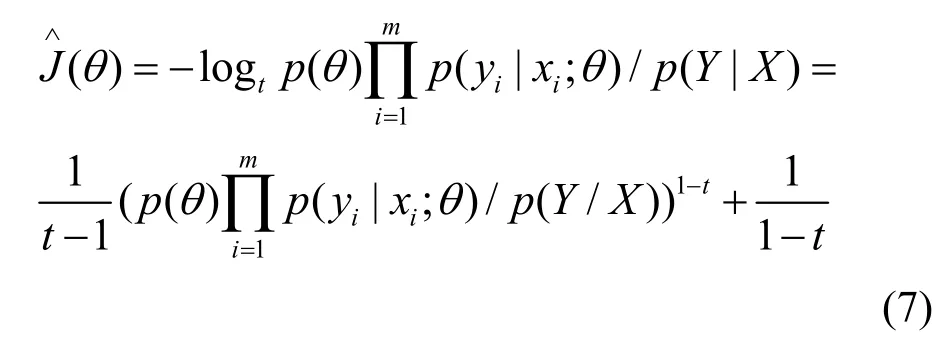
其中，p（Y/X）相对θ独立。利用式（2）、（3）和式（7），并令：

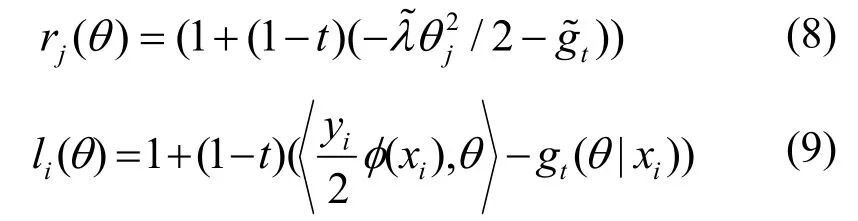
可以进一步得到：

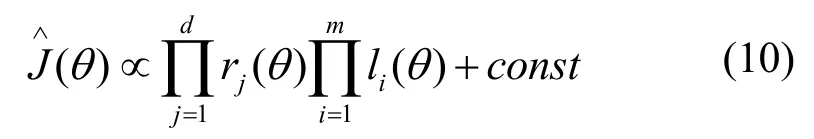
2　求解策略及收敛性分析［6］

根据凸多乘积规划［14］有：

其中，zn（θ）是正凸函数。设定dm N=+，对问题（11）的优化解可通过求解下列参数问题来获得：

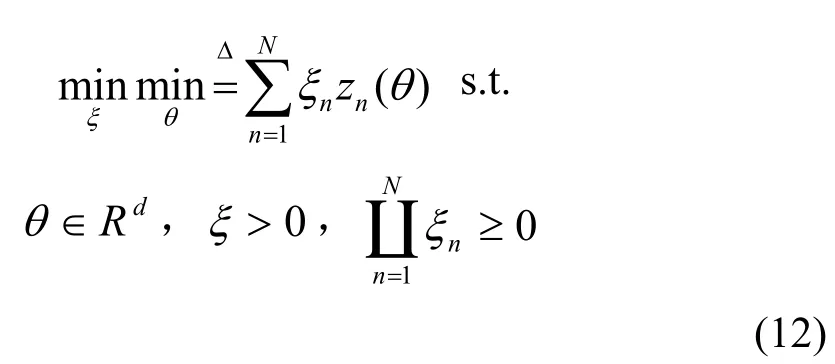
其中，ξn为每个样本xn的权重。求解（12）式的具体算法在文献［14］中提出，但是计算的成本随着N的指数倍增加。因此可以分别将θ和ξ作为变量做最小化分析，用坐标下降法来求解。

2.1以ξ为变量求解分析

由于目标函数对ξ而言是线性的，在可行区域是凸的，所以（12）式可以用凸优化问题的方法求解。

引入非负拉格朗日乘数γ≥0，（13）式可以写成

相对于ξn'的导数如下：

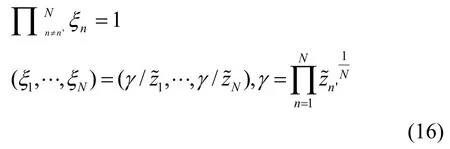
而（14）式中的ξn是每项zn（θ）的权。以上分析表明相对所有的n都是常数。如果（θ）变得非常大，nξ的影响就会减少。因此大损失点存在权重上限，这说明这个算法对异常值的鲁棒性非常好。

2.2以θ为变量求解分析

令ξ＞0，求解最佳θ。这一步和回归分析一样，但是每一成员都有一个权ξ，有：

这是一个标准的无约束的凸优化问题，它可以被任何现成的求解器求解，采用L-BFGS高斯-牛顿方法。这样需要求解梯度

其中，en表示d维向量包含一个在n阶坐标，别的地方都是零（即n阶单位矢量）。（y|x；）θ qt是的escort分布：

3　实证分析

3.1模型样本及财务指标的选择

首选选取沪深股市A股上市公司，要求规模相当且上市五年左右。从2005-2007年选取了51家ST公司，并按照大约1:1的比例选取了相同时间段的且上市以来从未被ST的51家正常公司，其中2005年共32家、2006年共28家、2007年共42家。

参考国内外相关资料［5-8］，根据盈利能力、债务能力、成长能力、营运能力、现金流量和资本结构，共选择了26个变量。自变量为Y，表示该公司是否会出现财务危机，如果为ST公司则表示出现了财务危机，用0表示；如果没有出现财务危机，则为非ST公司，用1表示。

由于有些财务指标没有显著差异，因此需要对样本数据进行显著性检验。本文采用SPSS对样本进行单样本K-S检验，判断是否服从正态分布。通过分析，发现大多数指标不服从正态分布。于是，采用非参数检验。非参数检验方法很多，有Mann-Whitney U检验、Kolmogorov-Smirnov Z检验、Moses极限反应和Wald-Wolfowitz 游程检验［16］。这里选用最常见的Mann-Whitney U检验。利用SPSS软件分析，将不能通过Mann-Whitney U检验的指标剔除，将剩下指标组成新的样本数据。

3.2模型实证分析结果

实验平台为 MATLAB7.1。利用最终保留下来的 16 个财务预警指标数据作为模型的输入，训练样本与测试样本的比为 2:1，训练样本共 68 家，测试样本 34 家。根据文献［6］可知非凸函数不容易受初值的影响，因此初值的选择可以有一定的随意性，选经过MATLAB仿真，没有加噪声的训练样本与测试样本的误差数据如表1，加入10%噪声后的仿真数据如表2。

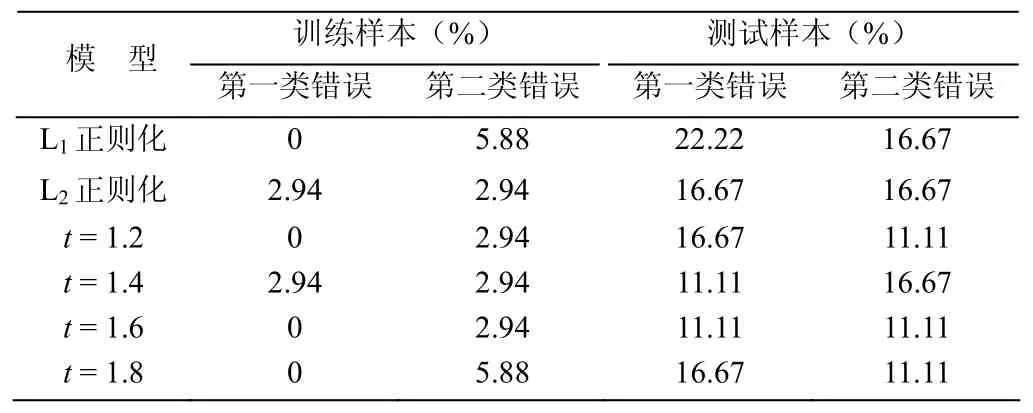
表1　噪声为0，仿真误差表Table 1　The error of the simulation when noise equals zero

由表1可知，在噪声为0的时候，用正则化模型和T逻辑回归模型的训练样本的正确率都非常高，但是对测试样本而言，T-logstic模型的正确率要高于正则化逻辑回归模型3～5个百分点。可见T逻辑回归模型具有较好的预见性。

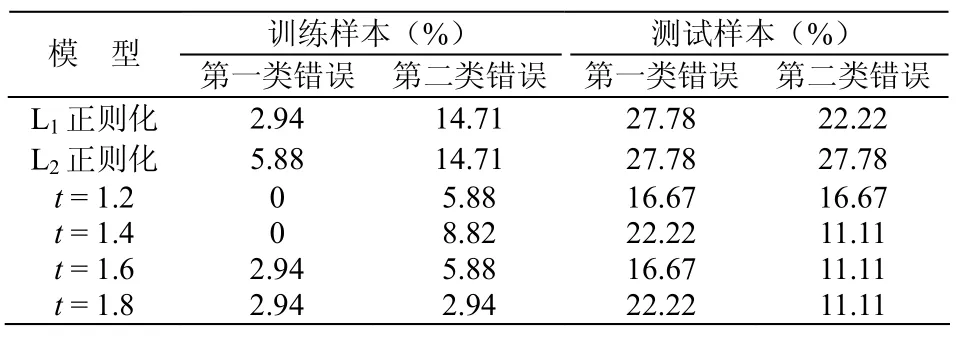
表2　噪声为10%，仿真误差表Table 2　The error of the simulation when noise equals 10%

加入10%的噪声后，整体的正确性都有所下降。L1正则化模型的训练样本的正确率由97.06%下降到91.18%，L2正则化模型的训练样本的正确率由97.06%下降到89.71%，而T逻辑回归模型的正确率下降与t的选择有关，但总体下降幅度不大，仅下降了0～3个百分点，特别是在t =1.8的时候，正确率没有受到噪声的干扰。测试样本的波动相对而言更大，L1正则化模型的训练样本的正确率由82.35%下降到76.46%，L2正则化模型的训练样本的正确率由85.29%下降到73.53%，T逻辑回归模型的训练样本的正确率也有所下降，但是幅度也不大，都维持在85%以上。

加入噪声至30%，训练样本与测试样本的误差变化趋势见图1，通过对比可以观察到T逻辑回归模型对噪声的干扰有较强的鲁棒性。虽然L1，L2正则化模型和T逻辑回归模型都随着噪声干扰的增加，误差率会提高，但是T逻辑回归的误差率要远低于正则化模型。随着噪声干扰的增加，测试样本的误差率增加幅度降低，T逻辑回归的误差率与t的取值相关性降低。

图1　噪声干扰下的训练样本（a图）与测试样本（b图）的误差变化Fig.1　The error rates of the training samples （a） and the testing samples （b） when noise equals 30%

4　结语

本文将t指数族中的学生分布引入逻辑回归，建立了上市公司的财务预警模型。经过仿真，将T逻辑回归模型与L1和L2正则化逻辑回归模型比较，证实该模型具有较好的预测功能，并有较强的抗噪声能力。在以后的进一步研究中，将考虑深入讨论T逻辑回归与初值选择的相关性，以及t的选择对T逻辑回归模型精度的影响。

［1］ 陈艳，张海君.上市公司财务预警模型的研究［J］.财经问题研究，2007，（6）:92-96.

［2］ 许珂，卢海.基于Logistic回归模型的房地产上市公司财务危机预警研究［J］.常州工学院学报，2012（4）:61-66.

［3］ 吴冬梅，朱俊，庄新田，等.基于支持向量机的财务危机预警模型［J］.东北大学学报:自然科学版，2010，31（4）: 601-604.

［4］ 刘遵雄，黄志强，孙清，等.SCAD惩罚逻辑回归的财务预警模型［J］.统计与信息论坛，2012，27（12）:21-26.

［5］ 刘遵雄，郑淑娟，秦宾，等.L1正则化Logistic回归在财务预警中的应用［J］.经济数学，2012，29（2）:106-110.

［6］ Ding N， Vishwanathan S V N.t-Logistic regression［C］.Advances in Neural Information Processing Systems，2008:294.

［7］ Buscema M， Breda M， Lodwick W.Training with Input Selection and Testing （TWIST） Algorithm: A Significant Advance in Pattern Recognition Performance of Machine Learning［J］.Journal of Intelligent Learning Systems and Applications， 2013， 5: 29-38.

［8］ Hastie T， Tibshirani R， Friedman J， et al.The elements of statistical learning: data mining， inference and prediction［J］.The Mathematical Intelligencer， 2005，27（2）: 83-85.

［9］ De Souza A M C， Tsallis C.Student's t-and r-distributions: Unified derivation from an entropic variational principle［J］.Physica A: Statistical Mechanics and its Applications， 1997， 236（1）: 52-57.

［10］ Naudts J.Generalized thermostatistics based on deformed exponential and logarithmic functions［J］.Physica A: Statistical Mechanics and its Applications， 2004， 340（1）: 32-40.

［11］ Naudts J.Generalized thermostatistics and mean-field theory［J］.Physica A: Statistical Mechanics and its Applications， 2004， 332: 279-300.

［12］ Naudts J.The q-exponential family in statistical physics［J］.Central European Journal of Physics， 2009，7（3）: 405-413.

［13］ Dawson R.Wittgenstein on pure and applied mathematics［J］.Synthese， 2014， 191（17）: 4131-4148.

［14］ Kuno T， Yajima Y， Konno H.An outer approximation method for minimizing the product of several convex functions on a convex set［J］.Journal of Global optimization， 1993， 3（3）: 325-335.

［15］ Zhou W J， Chen X L.On the convergence of a modified regularized Newton method for convex optimization with singular solutions［J］.Journal of Computational and Applied Mathematics， 2013， 239: 179-188.

［16］ 张文彤.世界优秀统计工具SPSS 11统计分析教程高级篇［M］.北京:北京希望电子出版社，2002:S91-92.

FINANCIAL EARLY-WARNING MODEL OF LISTED COMPANIES USING T-LOGISTIC REGRESSION

*XU Zheng1， LIU Zun-xiong2

（1.School of Electrical and Electronic Engineering； 2.School of Information Engineering， East China Jiaotong University， Nanchang， Jiangxi 330013， China）

The classic logistic regression has the risk of over fitting.It can be solved by the regularization technique of the statistical learning theory.Optimization of convex loss function can ensure that the regularized risk minimization problem converges to the global optimum， but learning algorithm of convex loss function is susceptible to noise.Then T-logistic regression was proposed to amend， introducing T distribution into logistic regression.The non-convex loss function is made up for the deficiency of convex loss functions.Due to the non-convex loss function difficulty to solve， we will be logarithmic the objective function， and convex multiplicative programming is used to solver parameters.Through empirical study， it is found that T-logistic regression model has a good predictability and is tolerant to label noise.

financial early-warning model； regularization technique； financial T-logistic regression； over fitting；non-convex loss function

TP311.13

ADOI:10.3969/j.issn.1674-8085.2015.02.002

1674-8085（2015）02-0006-05

2014-11-17；修改日期：2015-01-20

国家自然科学基金项目（61065003）；教育部人文社会科学研究项目（13YJC630192）；华东交通大学校立科研课题（09DQ04）作者简介：*徐征（1978-），女，湖北随州人，讲师，硕士，主要从事数理统计和非线性系统分析与建模研究（E-mail:187391733@qq.com）；刘遵雄（1965-），男，江西南昌人，教授，博士，主要从事机器学习和金融统计时序分析研究（E-mail: 153010729@qq.com）.