关于矩阵特征值理论的教学新设计

邓　勇

（喀什大学　数学与统计学院，新疆　喀什　844006）

关于矩阵特征值理论的教学新设计

邓勇

（喀什大学数学与统计学院，新疆喀什844006）

基于现行高等代数教材中关于矩阵特征值理论的行列式分析法，以Sheldon Axler的教材Linear Algebra Done Right为蓝本，介绍了矩阵特征值理论的非行列式观点，修改或重写了部分定理和证明.这种不使用行列式的简单证明不仅直观，而且开辟了一条通往高等代数主要目标——线性算子结构的新途径.

矩阵；特征值；行列式；特征子空间；教学设计

1　引　言

近几年，围绕高等代数课程的教学改革，许多学者都提出要加强高等代数与几何融合、推行问题型、体验式教学模式和坚持并加强教学工作的再创造性等教改新观点.其中，文献[1～3]紧扣几何为代数提供直观背景，代数为几何提供研究方法，论述了高等代数与解析几何课程一体化教学过程中的若干教学实践与认识，主张在关注代数思维的同时，突出几何直观教学来帮助学生理解和掌握抽象的代数概念和理论；文献[4]结合作者的教学实践，提出从内容与结构上对高等代数教材进行改革的设想；文献[5～6]立足于提升学生在独立的主动思考和实践研究过程中培养科学思维、严谨作风及创新能力，倡导“问题探究——学生主体”和“教学双中心”、“过程结果并重”的教学理念，并进行了一些大胆的有益尝试，效果明显.基于这些观点，近30年来，国内陆续出版了许多比较经典的高等代数教材.如，北京大学丘维声编著的《高等代数》；中国科技大学李炯生、查建国编著的《线性代数》；复旦大学姚慕生编著的《高等代数学》和清华大学张贤科编著的《高等代数》等.这些教材都比较全面地论述了矩阵理论和线性空间及其变换理论，而且表述形式非常现代化，反映出的核心观点就是强调高等代数与几何的融合，非常有见地[7].然而，在阐述矩阵的特征值理论时，它们却毫无例外地都以行列式为工具.这些教材为何如此处理，难道矩阵的特征值理论非要借助行列式吗？美国数学教授Sheldon Axler在1994年发表文章宣称“Down with determinants！”具体明白地表达了“反行列式”的革命思想.他的理由是行列式难理解、不直观，且是在缺乏动机的情况下被定义出来的.研究者对此颇有同感，因为矩阵特征值理论的形成并非缘于行列式，所以要使学生正确理解知识的形成过程，这种彻底抛开行列式的教学观点应该被提倡.

2　新教学设计的线路

矩阵的特征值理论必须围绕5个方面的基本问题展开：（Ⅰ）任意方阵A必有一特征值λ；（Ⅱ）方阵A的相异特征值个数小于等于n，即m≤n；（Ⅲ）确定特征值jλ的代数重数βj；（Ⅳ）任意特征值λj的几何重数不大于其代数重数；（Ⅴ）定义特征多项式.

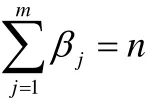
2.1特征分析的行列式法回顾

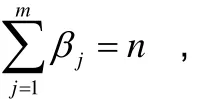
2.2特征分析的非行列式法设计

描述线性算子的结构是高等代数的中心任务之一.下面对矩阵特征值理论5个方面问题的基本阐述均不使用行列式，由此也开辟了一条理解线性算子结构的新途径.

第一，回答问题（Ⅰ）.为此，需先证明定理1，然后将定理1中的不变子空间X替换为后，实际上就回答了问题（Ⅰ）.

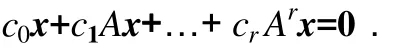
令s是使cs≠0的最大下标，显然0＜s≤r.以ci为系数构造一个r次多项式并分解因式，设为

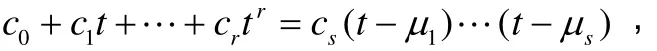
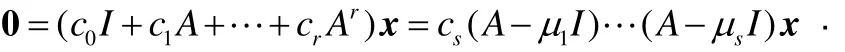
上式说明，等号右边的矩阵乘法算式中至少有一个μj和某个向量v≠0满足(A-μJI)v=0.换句话说，A必定有一个特征向量v∈X对应于特征值μj.

第二，回答问题（Ⅱ）.同样，问题（Ⅱ）的解决也是建立在如下定理2基础之上的.

定理2对应相异特征值λ1,λ2,…,λm的特征向量x1，…， xm必定线性无关[9].

因为对应于相异特征值λ1,λ2,…,λm的特征向量xj∈□n, (j=1,…,m)线性无关，而线性无关的n维向量总数不大于n，所以相异特征值总数m不大于n.这就回答了问题（Ⅱ）.

第三，回答问题（Ⅲ）.问题（Ⅲ）看似简单，其实不然.它不仅需要定义广义特征向量，还需讨论其性质特征.

定义1向量x≠0称为对应于特征值λ的广义特征向量，如果(A-λI)kx=0成立.其中k为满足此式的最小正整数，称为指标.特别地，当k=1时，广义特征向量即为一般特征向量.

如同特征向量构成特征子空间一样，广义特征向量与零向量所形成的集合N(A-λI)k也是□n的一个子空间，称为广义特征子空间[9].之所以不考虑k＞n的情况，是因为：

定理3若λ为n阶方阵A的一个特征值，则N(A -λI )k=N(A-λI )n.

证明设x≠0是对应于λ的（指标为k）广义特征向量.运用处理问题（Ⅰ）的相同手法，可以证明当(A-λI)kx=0时，{x, (A-λI)x, …, (A-λI)k-1x}是一线性无关向量组.于是，必有k≤n.考虑线性组合式

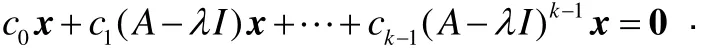
等号两边同乘(A-λI)k-1，并利用已知条件可得推出等号两边同乘(A-λI)k-2可得又可推出.连续运用这种方式，最终可证得

定义2特征值λj的广义特征向量组的维数称为其代数重数βj，即

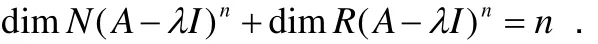
11

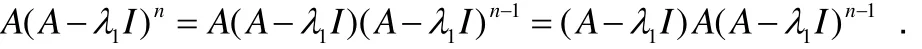
定理6子空间N(A-λI)n仅存在唯一的特征值λ.

证明设0≠x∈N( A-λI)n.若λ≠λ＇且Ax=λ＇x，则因此，但因此矛盾！故

既然广义特征子空间仅存在唯一的特征值，由此可推知对应于相异特征值的广义特征子空间互不相交.进而对应于相异特征值的广义特征向量必线性无关.这个结果是定理2的自然推广.

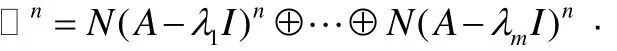
进而有

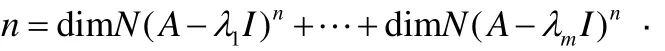
又因

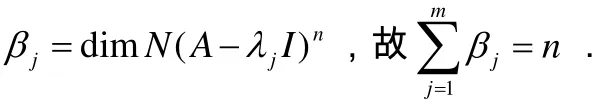
第四，回答问题（Ⅳ）.由N(A -λI)⊆N(A -λI )n可推出对应于特征值λ的线性无关特征向量个数必少于线性无关的广义特征向量个数.而对应λ的几何重数就是线性无关的特征向量个数，代数重数则等于线性无关广义特征向量的总数.因此，特征值λ的几何重数必不大于其代数重数.

第五，回答问题（Ⅴ）.根据上面讨论，一个n阶方阵A的特征多项式可定义为p(t)=(t -λ)β1…(t -λ)βm.值得注意的是，这里特征多项式诞生的时间节点刚好与用行列式定义特征多项式相反.即先说明A有n个特征值（含重数），然后才根据这个事实定义了特征多项式.显然，这才符合思维的逻辑顺序规律.

3　结　语

以行列式为基础的特征分析法以代数为导向，而非行列式的特征分析法却以几何（特征空间）为导向.上述研究提倡的非行列式的特征分析法不仅更清晰简单，而且能提供给学生更多的见识.为何现行的多数教科书仍然采用行列式方法来发展矩阵特征值理论呢？初次接触行列式的人多少对它诡异的计算方式感到困惑，想要掌握行列式的直观意义确实不容易.但不论真懂假懂，绝大多数学生对行列式的计算及基本性质还是生硬地接受了，这是既成的事实.因此，多数学生认为用行列式定义特征多项式是最为直接简明的论述方式，而且对Axler提倡的“反行列式”方法却不甚了解.由于教材的编写要充分考虑学生的知识背景与兴趣，现行绝大多数教材还是选择了利用行列式方法来发展矩阵的特征值理论.为有效弥补教学策略难以在课堂教学中完全实现的缺陷[10～13]，研究者结合个人的经验与体会，提出教学的几点建议与各位同行和读者商榷：一是在课堂教学中，应注意结合几何直观来讲授高度抽象的内容；二是在传授知识的过程中，为培养学生分析、解决问题的能力，应注重思想与方法的提炼；三是在上习题课时，应多给学生介绍相关的最新教研成果，以启发他们系统地多维度思考问题；四是应增加课后作业量，以克服学生能动口但不能动手的问题，因为数学只能做着学.

[1]郭民.高师院校代数与几何课程改革的探索与实践[J].数学教育学报，2007，16（4）：90–92.

[2]沈雁.线性代数教学中直观性应用的实践与思考[J].数学教育学报，2010，19（6）：86–88.

[3]郁金祥，刘锦萍.高等代数与解析几何的教学实践与认识[J].高等理科教育，2006，（3）：12–14.

[4]张志让.线性代数教材内容与体系结构改革的思考与实践[J].大学数学，2005，（2）：22–24.

[5]任北上，刘立明，李碧荣.问题型教学模式在高等代数教学中的探索[J].数学教育学报，2013，22（2）：95–98.

[6]郑毓信.数学教育领域中的三个新“教条”——关于数学课程改革深入发展的再思考[J].数学教育学报，2011，20（1）：5–9.

[7]庄瓦金.三十年来中国《高等代数》教材（教学）之管见[J].数学教育学报，2009，18（3）：91–95.

[8]Sheldon Axler. Linear Algebra Done Right (Second Edition) [M]. Published by Springer, 1997.

[9]蓝以中.高等代数简明教程(下册) [M].北京：北京大学出版社，2002.

[10] 孙敏.高等代数课程教改的思考和实践[J].数学教育学报，2010，19（3）：100–102.

[11] 吕世虎，曹春艳，叶蓓蓓.数学教育学学科建设三十年：回顾与反思[J].当代教育与文化，2014，（5）：55-59.

[12] 王光明，佘文娟，宋金锦.基于NVivo10质性分析的高效数学学习心理结构模型[J].心理与行为研究，2014，（1）：74-79.

[13] 王玉行.高等代数教学对学生形成和发展数学品质的意义及教学策略[J].数学教育学报，2007，16（3）：92–94.

New Instructional Design on Matrix Eigenvalues Theory

DENG Yong
（College of Mathematics and Statistics, Kashgar University, Xinjiang Kashgar 844006, China）

The theory of matrix eigenvalues by determinant characteristic analysis in the current majority of advanced algebra textbooks was reviewed briefly, then based on linear algebra textbook “Linear Algebra Done Right” of Sheldon Axler, the non-determinant viewpoint of matrix eigenvalues analysis is described, and some proofs of theorems are modified or rewritten. This simple proof without determinant is not only more intuitive, and opens up a new way of understanding linear operator structure that leading to the main goal of advanced algebra.

matrix; eigenvalues; determinant; eigenvalue subspace; instructional design

G642

A

1004–9894（2015）06–0044–03

[责任编校：陈隽]

2018–08–10

新疆维吾尔自治区高校科研计划重点项目——体上依赖参数方程组的数值方法（XJEDU2008I31）；喀什师范学院教改立项课题——喀什师范学院2012年度精品课程“高等代数”建设（KJG200806）

邓勇（1967—），男，四川遂宁人，教授，硕士生导师，主要从事数学课程与教学论研究．