加减应用题结构表征干预研究述评

郭兆明

（扬州大学　教育科学学院，江苏　扬州　225002）

加减应用题结构表征干预研究述评

郭兆明

（扬州大学教育科学学院，江苏扬州225002）

加减应用题结构表征包括基于图式教学、基于概念模型的问题解决和图式扩展教学3种策略.每种策略从图式图、运算和干预效果3个维度概述，研究发现：（1）3种策略为加减应用题设计了许多图式图，基于概念模型的问题解决策略的图式图更具有清晰性和概括性；（2）3种策略都趋于借助图式图、方程和数字家族来选择运算；（3）3种策略干预都有积极的效果；但基于图式干预策略文献较多，其它两种策略文献较少；对于数学学习不良的被试研究较多，其它类型的学生研究文献较少.研究者可以从被试、实施者、图式图、维持、概括和效果比较6个维度，深化加减应用题结构表征干预研究.

加减应用题；结构表征；干预；学习不良；图式图

加减应用题是指运用加法或减法运算解答的数学应用题，是小学低年级学生学习的重点，也是学习的难点.学生的应用题错误大多来源于问题结构表征的错误，而不是计算错误[1～2].特别对于数学学习不良学生，因为他们在注意、信息组织、工作记忆方面存在缺陷[3].故国外出现了许多结构表征干预研究，这里对结构表征干预研究进行概述和简评，指出未来进一步研究的方向，为干预提供有效的干预策略，为加减应用题的教学设计、课程设计提供心理学基础.

1　研究概述

加减应用题结构表征策略包括3种类型：基于图式教学（Schema-based Instruction）、基于概念模型的问题解决（Conceptual model-based problems solving）和图式扩展教学（Schema-broadening instruction）.3种策略都强调问题结构（图式）对问题理解和表征的作用.为了使学生形成问题图式，研究者们设计了各具特色的图式图（schematic diagrams），其目的在于帮助学习者组织信息和选择运算.图式图具有以下优势：首先，突出了结构特征，去掉了无关细节的干扰；其次，图形是可以用眼睛看的，使学生利用对于人类来说是非常容易的知觉推理；最后，图形可以再现情境或现实过程，而后者是认识的源泉[4].

1.1基于图式教学

基于图式的教学是美国特殊教育专家Jitendra教授提出的，目的在于对小学数学学习不良学生进行有效干预.

1.1.1图 式 图

一个被广泛接受的加减应用题分类是根据问题的语义结构将问题分为3种类型：合并题、变化题和比较题[4].合并题图式图包括两个部分集和一个总体集，共3个槽.变化题图式图包括开始集、变化集和结束集3个槽，比较题图式图包括比较集、标准集和差集3个槽.每个槽都可以填入已知数或未知数，未知数用“？”表示.

Jitendra等[5～7]设计了合并题、变化题和比较题的图式图（图1～3）；Jitendra等[8～9]对3种图式图进行了改进，合并题图式图出现了数量关系，而且用部分集和总体集方框的大小来提示哪个是总体集（图4）；变化题图式图多了一个箭头，使得变化过程更明确（图5）；比较题图式图变化较大（图6）：（1）图形更简洁；（2）出现了运算；（3）标准集和比较集标注为大数和小数，这样回避了比较集和标准集的比较.Jitendra等[10]对图式图又进行了改进，图式图中标注“大数（总体集）未知还是已知”（图7），这里只呈现比较题来例示；Jitendra等[11～12]对比较题图式图进行了改进，大数和小数用不同大小的圆来表示，有利于减少学生输入数据错误（图8）.

1.1.2运算

Jitendra等[5～7]选择运算的规则为：“求总数（大数）用加法，已知总数求其它数（小数）用减法.”从判别规则可以发现，3种类型的加减应用题都是基于部总关系（即部分与总体之间的关系）来判别运算.因此，识别“总数”是很重要的.合并题中总体集就是“总数”；对变化题来说，如果变化集变大，结束集充当“总数”，如果变化集变小，则开始集充当“总数”；对比较题来说，比较集和标准集哪个大就充当“总数”.Jitendra等[8～12]不需要依靠规则选择运算，先列出方程（未知数用“？”表示），例如，求“?-4=3”，不要求学生会解方程，而是依靠数字家族（number families）来得到运算，完成计算，即在美国数学课本中把3+4=7、称为数字家族（这4个式子是等价的）.学生通过数字家族，把“?-4=3”转化为“3+4=7”或“4+3=7”.

1.1.3干预效果

（1）干预的有效性.

Jitendra等[5]研究基于图式教学策略（下文简称“图式策略”）干预3个小学数学学习不良学生解决一步加减应用题的效果（图1～3）.干预提高了解题正确率，图式策略能够保持2—3周.Jitendra等[7]研究了使用此策略干预4个中学生数学学习不良学生解决一步和两步加减应用题的效果（图1～3）.图式策略提高了他们的解题成绩，图式策略可以保持2—4周.图式图与Jitendra等[5]一致，只不过两步应用题图式图要使用两个一步应用题图式图来表示，4个学生中有3个能够将解一步加减应用题策略迁移到两步加减应用题.Jitendra等[8]研究了使用此策略干预两个三年级低能力班级和一个特殊教育班级的有效性（图4～6），结果显示：在解决一步和两步加减应用题和计算上，后测比前测好；使用三年级异质样本（高、中、低）做验证性研究，也得到相同的结论.Jitendra[11]的基于图式教学策略干预提高了两个具有情感和行为障碍的学生解决一步加减应用题的能力（图1、5、8）.

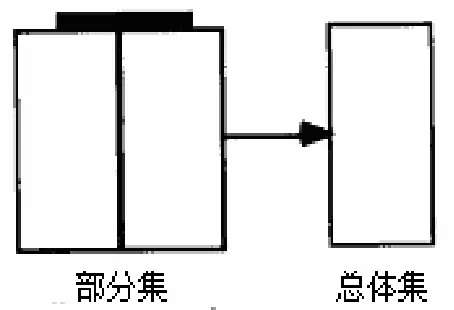
图1　合并题图式图

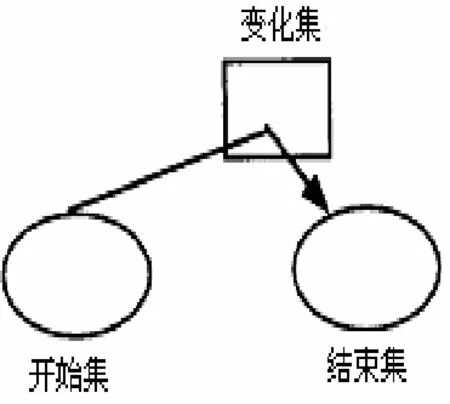
图2　 变化题图式图

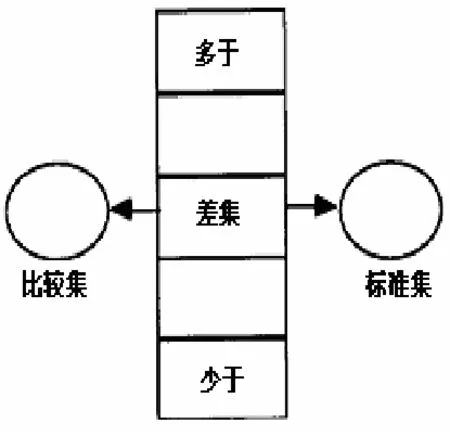
图3　比较题图式图

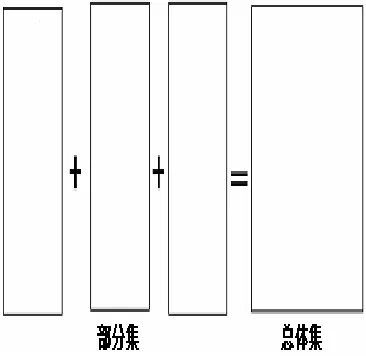
图4　合并题图式图

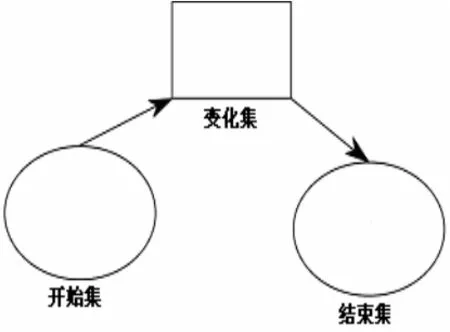
图5　变化题图式图

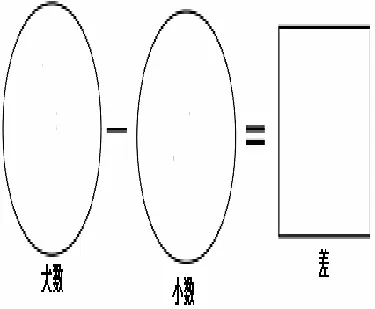
图6　比较题图式图

图7　比较题图式图

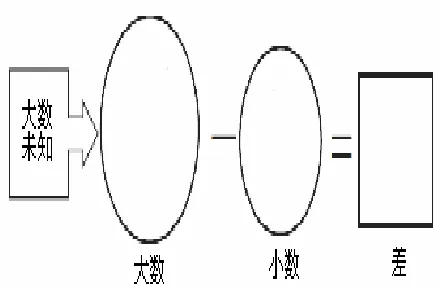
图8　比较题图式图

（2）干预效果比较.

Jitendra等[6，9～10]比较基于图式教学和通用策略教学（General Strategy instruction, GSI）效果.通用策略教学是指：（1）阅读和理解；（2）计划；（3）解答；（4）检查，它是美国小学数学教材中采用的解题策略.Jitendra等[6]比较了图式教学和通用策略教学干预34名小学数学学习不良学生解决一步加减应用题的效果（图1～3）.结果表明，两组的前后测成绩都提高了；两种解决应用题的教学策略都能被保持，也能概括到新情境中，但基于图式的教学策略在及时后测、延时后测和概括测验都优于通用策略教学.Jitendra等[9]比较了图式策略教学和通用策略教学促进三年级学生解决加减应用题的效果（图4～6）.结果表明，图式策略教学比通用策略教学在提高学生后测和维持测验上数学问题解决技能方面更有效.Jitendra等[10]比较了图式策略和通用策略教学促进三年级学生解决加减应用题和计算技能的效果（图1、5、7）.研究结果表明，图式策略和通用策略教学都提高了应用题解决成绩和计算成绩.而且，图式策略组在应用题解决的测量上显著高于通用策略教学组的成绩.然而，这个差异效果没有维持很长时间.

Jitendra等[12]比较了使用基于标准课程（standard-based curriculum, SBC）与图式教学课程干预数学学习困难学生的效果（图1、5、8）.基于标准课程教学是基于探究的、以学生为中心的教学（例如，学生创造新算法和新表征）.而基于图式教学是以教师为主导的教学（例如，传统算法、教师提供图式表征）.结果表明，干预方法与应用题问题解决后测以及维持测验都存在交互效应，即对前测应用题解决成绩高的学生来说，图式组学生后测和维持成绩超过基于标准课程组，而对于前测应用题成绩低的学生来说，图式组学生后测和维持成绩低于基于标准课程组.然而，在加减计算题测验、数学和阅读成就测验的成绩没有显著差异.

Leh和Jitendra[13]比较了计算机辅助教学（computermediated instruction, CMI）和教师实施的教学（teachermediated instruction, TMI）对于三年级数学困难学生加减应用题的影响（图1、5、6）.结果表明：在后测和4周后的维持测验，两个组无显著差异.而且，应用题问题解决能力没有迁移到标准化数学成就测验.这说明谁传输教学不重要，关键在于教学策略设计，因为这两种教学都强调问题结构，以及其它教学成分（例如，及时反馈）.

1.2基于概念模型的问题解决

在Jitendra的基于图式教学基础上，Xin[14]提出了基于概念模型的问题解决策略，强调用方程表征数量关系.

1.2.1图 式 图

Xin[14]的图式图（图9）由两个部分集和一个总体集的3个成分组成，两个部分集之间是加法关系，而它们的和与总体集是相等关系.在每个图式的3个槽中，填入已知数或者未知数，未知数用字母x表示.

在不同类型的加减应用题中，3个成分表示不同的名称.例如，在合并题中（Susan有4支铅笔，Tom有8只铅笔，他们一共有多少支铅笔？），Susan和Tom的铅笔数分别充当两个部分集，这两个部分集构成总体集（图9）；而在变化题中（Susan有12颗糖果，她给4颗给Tom，Susan现在有多少颗？）.Susan开始的糖果数是总体集，而Susan给Tom的糖果数以及她现在的糖果数充当两个部分集（图9）；在比较题中（Susan有12颗糖果，Tom有4颗糖果，问Susan比Tom多多少糖果？），Tom的糖果数（小数）、Susan比Tom多的糖果数充当两个部分集，Susan的糖果数充当总体集（大数）（图9）.因此，在不同类型问题中，部分集（总体集）代表不同的集合.创新在于：使用一个图式图来表征3种类型的问题.

1.2.2运算

基于概念模型的问题解决策略不需要依靠规则选择运算，先列出方程（未知数用x表示），然后，利用数字家族来得到运算，完成计算.

1.2.3干预效果

Xin[14]研究了基于概念模型表征干预5个四（五）年级数学学习不良学生解决一步加减应用题的效果（图9）.结果表明，基于概念模型的表征提高了学生解决加减应用题的成绩，促进了前代数概念和技能的获得.

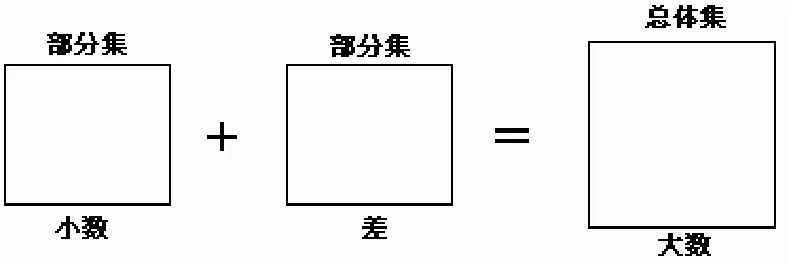
图9　合并题及变化题和比较题共同的图式图

1.3图式扩展教学

Fuchs[15]在Jitendra基于图式教学的基础上，提出了图式扩展教学，它包括4个成分：（1）教学生理解问题类型的数学结构；（2）教学生识别问题类型的图式；（3）教学生选择运算；（4）教学生迁移图式到新问题.前3步与Jitendra相似，此研究创新在于：教学生迁移图式到新问题（成分4）.图式扩展通过问题的表面变异来实现，包括：（1）增加无关信息；（2）使用图形、表格、曲线图表示相关信息；（3）使用两位数字（原来问题中是一位数字）.Fuchs通过表面变异加深学生对图式的认识.图式扩展教学的理论基础是Wagner[16]提出渐进式迁移的观点.Wagner[16]认为：迁移不是被理解为全或无的，而是渐进式地增长的.即概括不是一步完成的，而是不断逐步概括的结果.也就是说，不是通过两个样例的概括，获得一个图式，然后，就可以迁移到其它情境不同的问题中去.事实上，新手和数学学习困难学生在识别不同情境的相似性结构方面存在困难，只能通过提供给他们解决不同情境的问题，他们能够逐渐建构知识的框架（图式）.

1.3.1图 式 图

Fuchs[15]设计了合并题、变化题和比较题的图式图（图10～12）.数量关系在图式图中清晰呈现.对合并题来说，部分集+部分集=总体集（图10），对变化题来说，开始集±变化集=结果集（图11）；对于比较题来说，小数+差=大数（图12），未知数用字母x表示.

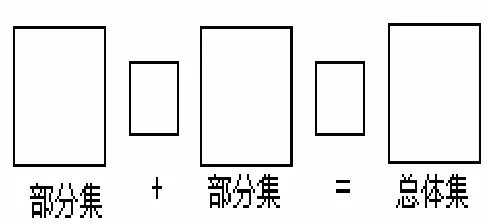
图10　合并题图式图

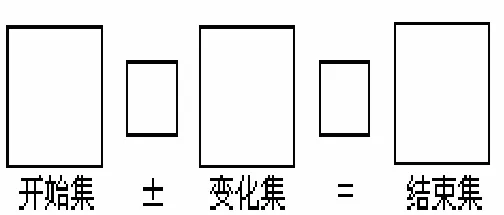
图11　变化题图式图

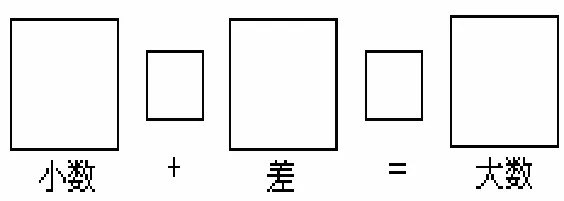
图12　比较题图式图

1.3.2运算

基于概念模型的问题解决策略不需要依靠规则选择运算，先列出方程（未知数用x表示），然后，利用数字家族来得到运算，完成计算.

1.3.3干预效果

Fuchs[15]比较图式扩展教学与正常课堂教学对三年级数学和阅读困难学生解决加减应用题的干预效果（图10～12）.结果发现，图式扩展教学组的成绩优于普通课堂教学组.

Fuchs[17]比较了图式扩展教学策略和通用策略教学干预270名二年级学生解决加减应用题的效果（图10～12）.图式扩展教学解决应用题成绩更优，并且促进了学生的代数推理.

2　简　评

基于图式教学、基于概念模型的问题解决和图式扩展教学这3种策略具有共同特点，即都强调问题结构（图式）对问题理解和表征的作用，通过设计图式图，促进学生形成问题图式.但是这3种策略在图式图、运算选择和干预研究3方面存在差异.

2.1图 式 图

2.1.1关系的清晰性

Jitendra[5～7]的图式图（图1～3）上未标明变量之间的关系.但Jitendra[8～12]（图4～8）的合并题和比较题图式标明了集合之间的数量关系，但变化题图式图还未标明集合之间的数量关系.Xin[14]和Fuchs[15]的图式图标明了集合与集合之间的关系.

2.1.2图式的层次性

在日常经验的基础上，儿童产生出相应的认知加工图式，比如，变化图式、比较图式和合并图式.然后，在正规的数学教育影响下，儿童将这一系列图式整合成“部总关系推理图式”.变化图式、比较图式和合并图式可以被看作儿童在解决简单加减应用题时形成的初级图式，而“部总关系推理图式”是在此基础上形成的高级认知图式[18].因此，Jitendra和Fuchs建立的是初级认知图式，而Xin建立的是高级认知图式，为3种加减应用题只建立一个图式“部分+部分=总体”.

2.2运算

基于图式教学起初强调算术方法，强调运算的选择，学生不得不记住所有类型的规则，运用规则来选择运算（算术方法）[5～7].后来，Jitendra等[8～12]依靠方程列出算式（代数方法）.基于概念模型的问题解决方法和图式扩展教学都依靠方程列出算式（代数方法），这说明依靠方程来列式（代数方法）是一种趋势.

2.3干预效果

从干预效果来看，基于图式的教学、基于概念模型的问题解决和图式扩展教学都产生了积极的效果，不仅提高了后测的成绩，策略能够保持一段时间，部分策略还能概括到新情境中去.从效果比较来看，Jitendra进行了系统的研究：基于图式教学优于通用策略教学，与多媒体辅助教学效果无差异，优于基于标准课程的教学.这里共综述12篇加减应用题表征干预研究，其中，基于图式教学共9篇，被试是数学学习不良（困难）的学生为8篇，因此，基于图式干预策略文献较多，其它两种策略文献较少；对于数学学习不良的被试研究较多，其它类型的学生研究文献较少.

3　进一步研究的方向

3.1被试

基于图式教学研究的被试分别为：学习不良学生、存在失败危险的学生（at risk）、普通学生（成绩居于上、中、下）、情感和行为障碍的学生，对于普通学生和存在失败危险的学生（以成绩低为标志）的研究有待加强，还可以研究数学/阅读双差生与单科差生以及智力低下的学生.基于概念模型的问题解决和图式扩展教学研究的被试类型较少，需要进一步研究.

3.2实 施 者

基于图式教学的干预实施者分别为：研究者、教师、社区的非专业人员（家长、大学生等）、计算机，能否尝试用同伴（优秀的学生）来实施干预？有待进一步研究.基于概念模型的问题解决和图式扩展教学都是研究者实施干预，其他人能否实施干预有待进一步研究.

3.3图 式 图

基于图式教学、图式扩展教学策略每种类型都有一个图式图，共有3种图式图，基于概念模型的问题解决策略图式图只有一个统一的图式图，不需要判断问题类型了，也减轻了记忆负担，但是图式层次性提高了，图式层次性越高，学生接受就越困难[19～23]，虽然Xin[14]进行过个体干预研究，但这还需要进一步研究，例如，做实验组和控制组的对照研究.利用图式图帮助选择运算，3种策略都有相同的趋势是利用方程来列式，利用数字家族来计算，存在的问题是数字家族在美国小学数学课本中20以内的数较多，如果数字较大就不能运用此方法计算了，这个问题如何处理？

3.4维持

基于图式教学研究的维持时间分别为：1—2周、2—3周、6周、12周，但基于概念模型的问题解决和图式扩展教学只是进行了干预有效性的及时测验，没有施测延时测验，因此，干预策略的维持时间长短有待进一步研究.

3.5概括

基于图式教学研究的概括测验分别是：一步应用题→两步应用题→州数学测验.基于概念模型的问题解决和图式扩展教学未施测概括测验，因此，干预策略迁移的远近有待进一步研究.

3.6效果比较

基于图式教学与通用策略教学、基于标准的课程教学、计算机辅助教学进行了比较.还可以进一步进行效果比较研究：（1）基于图式教学的图式图进行了多次修改，这些图式图之间的效果比较；（2）基于图式教学、基于概念模型的问题解决、图式扩展教学的效果比较；（3）3种问题结构表征策略与自我调节策略的效果比较.

从以上6个维度，可以深化加减应用题结构表征策略干预研究，为加减应用题的教学设计、课程设计提供心理学基础.

[1]Anand P G, Ross S M. Using Computer-Assisted Instruction to Personalize Arithmetic Materials for Elementary School Children [J]. Journal of Educational Psychology, 1987, (79): 72-78.

[2]Decorte E, Verschaffel L, De Win L. Influence of Rewording Verbal Problems on Children’s Problem Representations and Solutions [J]. Journal of Educational Psychology, 1985, (77): 460-470.

[3]Gonzalez J E J, Espinel A I G. Is IQ-Achievement Discrepancy Relevant in the Definition of Arithmetic Learning Disabilities [J]. Learning Disability Quarterly, 1999, (22): 291-301.

[4]周新林，张梅玲.加减文字题解决研究概述[J].心理科学进展，2003，（6）：642-650.

[5]Jitendra A K, Hoff K. The Effects of Schema-Based Instruction on the Mathematical Word-Problem-Solving Performance of Students with Learning Disabilities [J]. Journal of Learning Disabilities, 1996, 29(4): 422-431.

[6]Jitendra A K, Griffin C , McGoey K, et al. Effects of Mathematical Word Problem Solving by Students at Risk or with Mild Disabilities [J]. The Journal of Educational Research, 1998, (91): 345-355.

[7]Jitendra A K, Hoff K, Beck M. Teaching Middle School Students with Learning Disabilities to Solve Word Problem Using a Schema-Based Approach [J]. Remedial and Special Education,1999, 20(1): 50-64.

[8]Jitendra A K, Griffin C, Dearline-Buchman A, et al. Mathematical Word Problem Solving in Third Grade Classrooms [J]. Journal of Educational Research, 2007, 100(5): 283-302.

[9]Jitendra A K, Griffin C, Haria P, et al. A Comparison of Single and Multiple Strategy Instruction on Third Grade Students’ Mathematical Problem Solving [J]. Journal of Educational psychology, 2007, 99(1): 115-127.

[10]Jitendra A K, Star J, Starosta K, et al. Improving Students’ Learning of Ratio and Proportion Problem Solving: The Role of Schema-Based Instruction [J]. Contemporary Educational Psychology, 2009, (34): 250-264.

[11]Jitendra A K, George M P, Sood S, et al. Schema-Based Instruction: Facilitating Mathematical Word Problem Solvingfor Students with Emotional and Behavioral Disorders [J]. Preventing School Failure, 2010, 54(3): 145-151.

[12]Jitendra A K, Rodriguez M, Kanive R, et al. Impact of Small-Group Tutoring Intervention on Mathematical Problem Solving and Achievement of Third-Grade Students with Mathematics Difficulties [J]. Learning Disability Quarterly, 2013, 36(1): 21-35.

[13]Leh J, Jitendra A K. Effects of Computer-Mediated Versus Teacher-Mediated Instruction on the Mathematical Word Problem-Solving Performance of Third-Grade Students With Mathematical Difficulties [J]. Learning Disability Quarterly, 2012, 36(2): 68-79.

[14]Xin Y P, Wiles B, Lin Y Y. Teaching Conceptual Model-Based Word Problem Story Grammar to Enhance Mathematics Problem Solving [J]. The Journal of Special Education, 2008, 42(3): 163-178.

[15]Fuchs L S, Seethaler P M, Powell S R, et al. Effects of Preventative Tutoring on the Mathematical Problem Solving of Third-Grade Students with Math and Reading Difficulies [J]. Except Child, 2008, 74(2): 155-173.

[16]Wagner J F. Transfer in Pieces [J]. Cognition and Instruction, 2006, 24(1): 1-71.

[17]Fuchs L S, Zumeta R O, Schumacher R F, et al. The Effects of Schema-Broadening Instruction on Second Graders’Word-Problem Performance and Their Ability to Represent Word Problems with Algebra Equations: A Randomized Control Study [J]. The Elementary School Journal, 2010, 110(4): 440-463.

[18] 郭兆明，宋宝和，张庆林.数学应用题图式层次性研究[J].数学教育学报，2006，15（3）：27-30.

[19] 张夏雨，喻平.基于关系—表征复杂性模型的问题图式等级性研究[J].数学教育学报，2009，18（4）：46.

[20] 李善良.数学概念表征层次的研究[J].数学教育学报，2005，14（4）：35-37.

[21] 张夏雨，喻平.不同学业水平学生数学问题图式的差异性研究[J].数学教育学报，2011，20（1）：45-48.

[22] 罗奇，唐剑岚.数学问题表征与数学问题图式[J].数学教育学报，2013，22（2）：19-22.

[23] 郭兆明，宋宝和，张庆林.代数应用题图式研究概述[J].数学教育学报，2007，16（4）：20-23.

Review on the Intervention Study on the Structural Representation for Add and Subtraction Word Problems

GUO Zhao-ming
(Department of Education Science, Yangzhou University, Jiangsu Yangzhou 225002, China)

There are three structural representation strategies for add and subtraction word problems, including Schema-based Instruction, Conceptual model-based the problems solving and Schema-broadening Instruction. Each strategy has been outlined from three dimensions of schematic diagrams, operation and intervention effect. The study has found that: (1) three strategies design lots of schematic diagrams about add and subtraction word problems; conceptual model-based problems solving has advantages in the schema clarity and schema generalization; (2) all of three strategies tend to select operation by schematic diagrams and the equation and number families; (3) the three intervention strategies all have positive effects, but Schema-based Instruction has more research literatures; subject on mathematical learning disabilities has more research literature; researchers can make the further studies on the intervention study for add and subtraction word problems from six dimensions of participants, subjects, schematic diagrams, maintaining, generalization and effect comparison.

add and subtraction word problems; structural representation; intervention; learning disabilities; schematic diagrams

G420

A

1004–9894（2015）06–0080–05

[责任编校：周学智]

2015–07–06

国家社会科学基金教育学一般课题——高职院校职业性向测试分析研究（BJA090056）

郭兆明（1966—），男，江苏扬州人，副教授，博士，主要从事学习心理研究．