复合材料层合板结构固化过程数值分析方法研究
2015-10-22彭亮毛伟赵美英
彭亮,毛伟,赵美英
(西北工业大学航空学院,陕西西安 710072)
复合材料层合板结构固化过程数值分析方法研究
彭亮,毛伟,赵美英
(西北工业大学航空学院,陕西西安 710072)
为了研究复合材料层板结构在固化过程中的温度场与固化度场分布情况,对ABAQUS子程序进行了二次开发,构建了不同固化动力学方程的子程序模块,实现了层合板固化过程的三维数值模拟。通过算例验证,所建立的数值分析方法能精确求解固化过程中的温度场和固化度场。基于该方法,进一步讨论了层合板边界条件、厚度、升温速率对温度场和固化度场的影响。上述研究方法具有较强的适用性,对改善固化工艺参数,控制结构固化变形具有一定的指导意义。
固化过程;边界条件;ABAQUS;有限元法
复合材料层合板在固化阶段,不仅层合板外部环境温度变化,而且层合板内部固化反应产生化学放热,两者相互影响,是一个复杂的耦合过程,导致层合板内部产生复杂的温度梯度。这种不均匀分布的温度场和固化度场,将在复合材料内产生热应力和变形,是复合材料制品中产生诸如尺寸误差、翘曲等缺陷的根本原因。因此,研究复合材料层合板在固化工艺过程中的温度和固化度分布及其变化规律,对提高复合材料工艺质量有重要意义[1]。
近年来对树脂基复合材料固化过程的有限元模拟取得了一定进展。Loos等[2]采用模块化方法研究层合板固化过程,针对AS4/3501-6单向层合板建立了一维数值模型;Bogetti等[3]采用二维有限元方法数值模拟了任意截面形状和边界条件层合板的固化过程;杨正林等[4]采用有限元与有限差分相结合的方法分析了二维层合板模型的固化变形;Cheung、张纪奎等[5-6]用有限元方法研究了三维条件下的固化过程。
由于固化过程中温度场和固化度场耦合问题的复杂性,研究者基本上都是自行编制程序来实现数值仿真,增加了研究的难度和周期,而且程序的适用性也受到限制。本文从正交各向异性材料的三维热传导方程和固化动力学方程出发,基于有限元软件ABAQUS进行二次开发,实现了树脂基复合材料固化过程的三维数值模拟,通过对2种材料体系的固化过程进行了算例验证,证明了程序的正确性,并讨论了层合板边界条件、厚度、升温速率对温度场和固化度场的影响。
本文研究所涉及的玻璃纤维/聚酯树脂的固化动力学方程属于n级反应模型[7],AS4/3501-6的固化动力学方程为自催化反应模型[8],当采用不同固化动力学方程时,只需依据利用Fortran语言在ABAQUS子程序的基础上进行编辑即可完成,因而具有更强的适用性,缩短了程序的编写周期。可用于分析复杂形状和边界条件下结构固化过程的温度场和固化度场,具有较强的适用性,对改善复合材料结构固化工艺参数具有指导意义。
1 热传导控制方程和固化动力学方程
热固性树脂基复合材料的固化过程是一个热与化学反应相互耦合的过程。复合材料构件内部的温度分布由向复合材料的传热速率和固化反应产热速率共同决定,复合材料固化温度场的分析本质上是一个具有非线性内热源的热传导问题,其中内热源是树脂基体固化反应放出的热量。通过对该热传导问题的求解,可以得到复合材料在固化过程中任意时刻、位置的温度及固化度。由于固化阶段树脂基本不发生流动,可忽略对流传热影响,则根据Fourier热传导定律和能量平衡原理建立该问题的热传导控制方程:
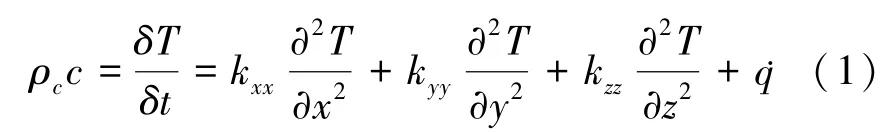
式中:ρc、c、kii(i=x,y,z)分别为复合材料的密度、比热、各向异性的热传导系数,内部热源项q□为树脂发生化学反应放出的热量,可以表示为:

式中:ρr为树脂密度,Hr为固化反应完成时单位质量树脂放出的总热量,α为树脂固化度,t为时间。
树脂的固化反应决定了热传导控制方程中内热源的热量大小,综合各类文献的研究方法,对固化动力学模型的表征方法主要有2种:微观水平(力学的)和宏观水平(唯象的)。其中唯象模型以化学反应动力学为主要特征,忽略各组分之间相互作用的细节,也不关注树脂的组成或配方,是最被广泛使用的方法。
大多数唯象模型以方程(3)、(4)为基础:

式中,f(α)为固化机理函数,由实验数据确定;K(T)为固化速率系数,用阿累尼乌斯方程表示:
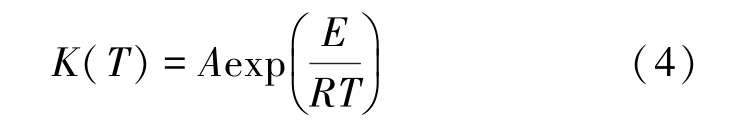
式中:A为频率因子;E为活化能;R为普适气体常数;T为温度。
根据树脂反应机理函数f(α)的形式,可以将现有模型分成n级反应模型和自催化模型2类,方程(5)和(6)的化学动力学模型分别属于n级反应模型和自催化反应模型。

式中:k1和k2可用阿累尼乌斯方程表示为:

式中,A1,A2,ΔE1,ΔE2为实验确定的常数。
2 基于ABAQUS用户子程序的温度场和固化度场模拟
ABAQUS具有强大的非线性分析能力,能很好地解决热-力耦合问题。本文主要运用ABAQUS/ Standard提供的HETVAL、USDFLD用户子程序,而在对流换热条件和温度边界条件比较复杂的模型进行定义时,使用了FILM和DISP子程序。
固化过程中树脂固化放热的模拟是通过子程序HETVAL定义热源项来实现的。该子程序用来在传热分析中定义内部生热与由于产热导致的热流,允许内部生热依赖于状态变量;子程序USDFLD对STATEV的任何更新都可传递到HETVAL中。
表征化学反应程度的固化度场通过用户定义场在材料属性中进行定义,定义中用使用了用户子程序USDFLD。状态变量可以在USDFLD中更新,然后传递到子程序HETVAL中。
温度场和固化度场的耦合求解如图1所示。

图1 温度场与固化度场耦合求解流程图
在子程序HETVAL中,通过固化动力学方程得到固化速率和固化度,并存储在状态数组STATEV中,更新后的STATEV数组传递到子程序USDFLD以得到固化度场;固化反应放热通过FLUX模块计算,产生的热量传递到ABAQUS热分析模块中得到新的温度场,并利用新温度计算得到固化速率和固化度,如此循环,直到固化过程结束。
3 算例及程序验证
根据上述温度场和固化度场的耦合求解流程,基于用户子程序对ABAQUS进行二次开发,编写了用于计算树脂基复合材料固化过程的子程序。本文采用了2个算例对不同固化动力学模型进行了验证。
3.1算例1
[5],采用[0/90]铺层的玻璃纤维/聚酯树脂层合板,长宽均为15.24 cm,厚为2.54 cm,共42层。玻璃纤维/聚酯树脂固化动力学经验公式为:
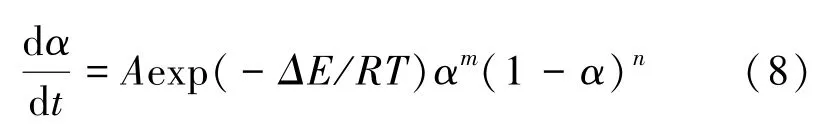
该固化动力学方程属于n级动力学模型,热力学参数如表1所示,固化动力学参数如表2所示,其中R为普适气体常数,取8.314。
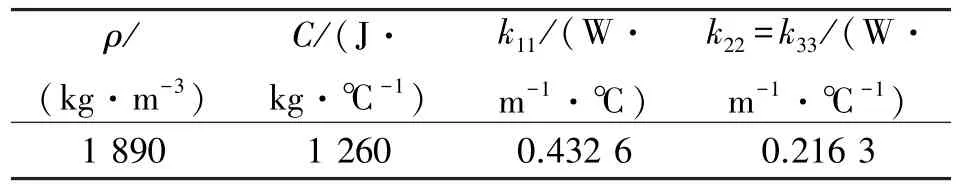
表1 玻璃纤维/聚酯树脂的热力学参数

表2 玻璃纤维/聚酯树脂的固化动力学参数
边界条件用对流换热系数h与导热系数k11的比值表示。上表面h/k11=87 m-1,下表面h/k11= 125 m-1,四周绝热。计算得到该层合板中心点温度和固化度历程,结果如图2a)和图2b)所示。由结果可知,温度和固化度均与实验结果符合良好,从而验证了程序针对n级动力学模型的正确性。
3.2算例2
参考文献[5],算例2采用[0/90]铺层的AS4/ 3501-6层合板,几何模型和算例1相同,长宽均为15.24 cm,厚为2.54 cm,共42层。AS4/3501-6固化动力学经验公式如下:
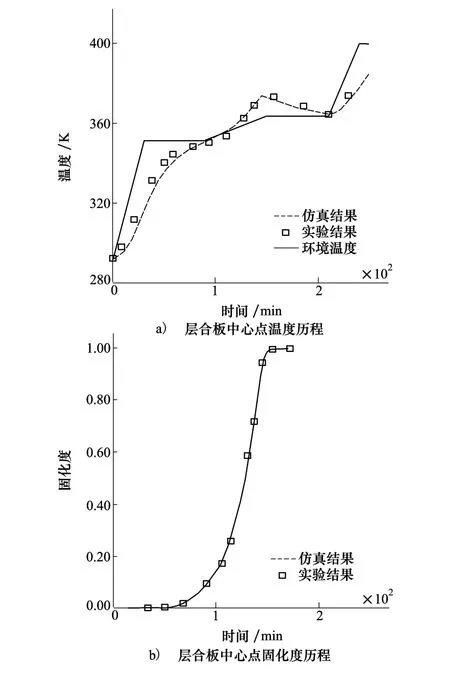
图2 玻璃纤维/聚酯树脂层合板中心点温度、固化度历程
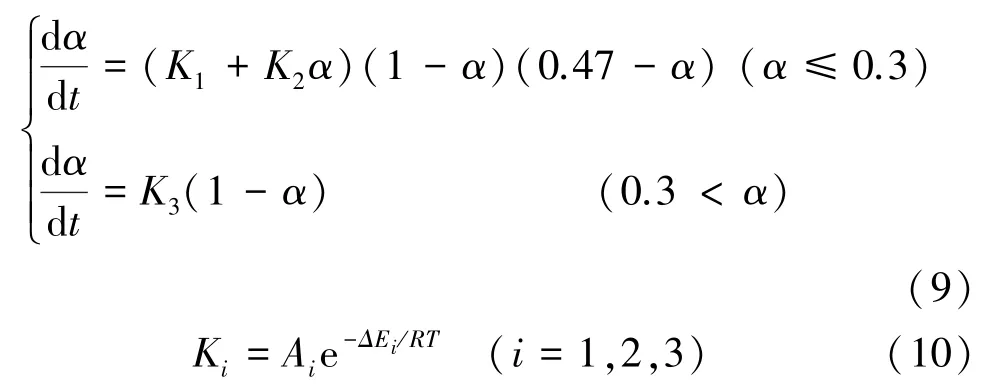
式中,K1、K2及K3分别为3501-6树脂体系的反应速率常数,A1、A2及A3分别为其频率因子,ΔE1、ΔE2及ΔE3分别为其活化能。可以看出,AS4/3501-6复合材料属于自催化动力学模型,以分段函数给出,以固化度达到0.3时作为分界点,0.3前后采用不同的固化动力学模型。

表3 AS4/3501-6的热力学参数

表4 AS4/3501-6的固化动力学参数
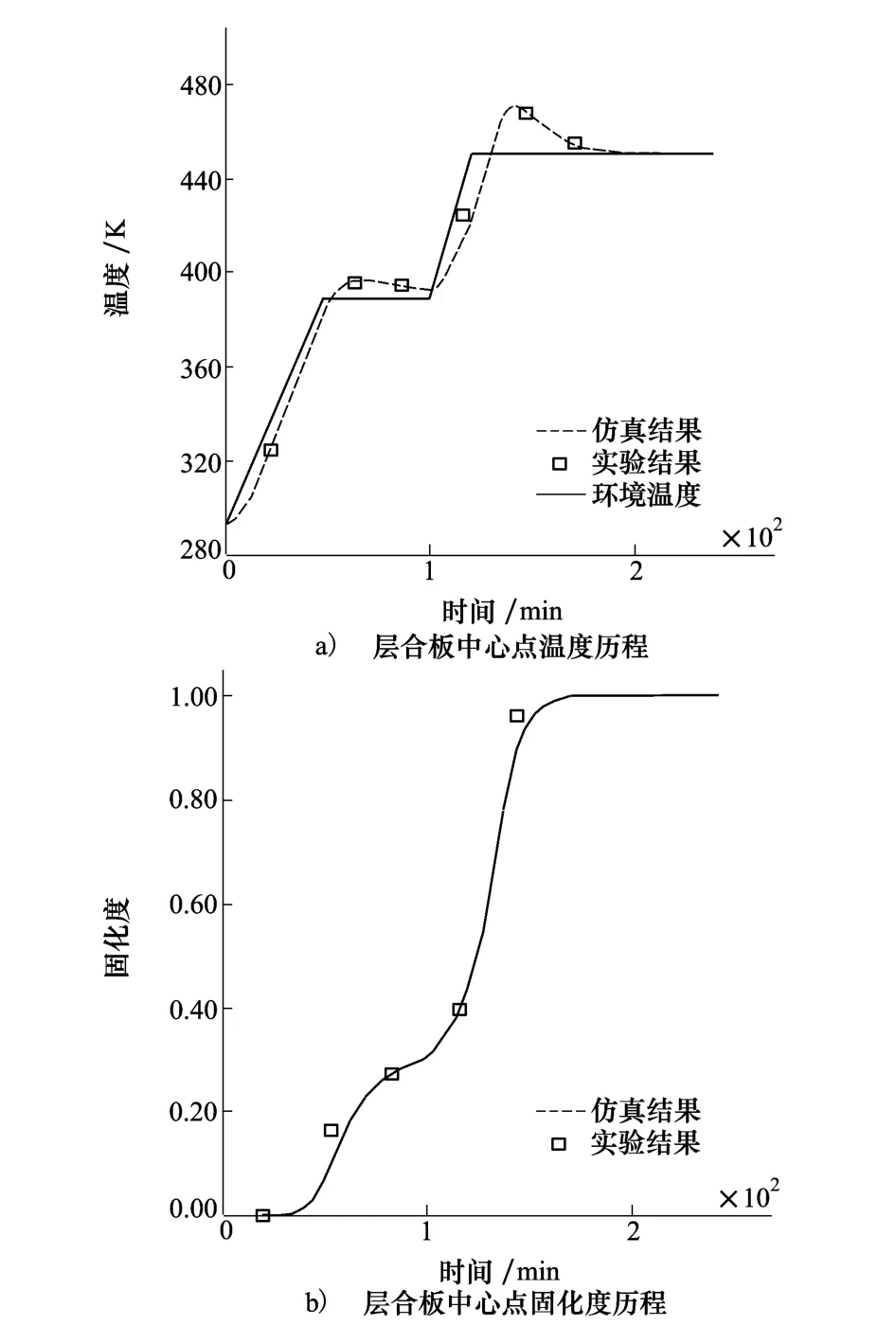
图3 AS4/3501-6层合板中心点温度、固化度历程
给定边界条件与算例1中相同。图3a)和图3b)分别为该层合板中心点温度和固化度历程,与文献实验结果进行比较,可以看出符合性较好,验证了程序针对自催化模型时的正确性。
4 分析与讨论
由计算结果可知,边界条件、厚度、升温速率对层合板温度场和固化度场均有影响。以下讨论中,除了研究厚度对温度场和固化度场的影响时,试件厚度不同外,在研究边界条件、升温速率对温度场和固化度场的影响时,层合板厚度均为2.54 cm;中心点指的是中间层(z=t/2)处。
4.1边界条件的影响
热传导问题有3类边界条件:①Dirichlet边界条件,即已知温度的边界条件;②Neuman边界条件,即已知热流密度的边界条件;③Robin边界条件,即已知对流换热系数的边界条件。第3类边界条件中,当对流换热系数h→∞时,边界条件就转化为第1类边界条件;当h→0时,边界条件就转化为第2类边界条件。故可通过改变h的大小来改变边界条件和特征。本文用h/k的比值变化来表示边界条件的改变,其中k为边界法向方向的热传导数,分别取h/k=100 m-1和500 m-1作为层合板上、下表面的边界条件,侧面仍为绝热边界。
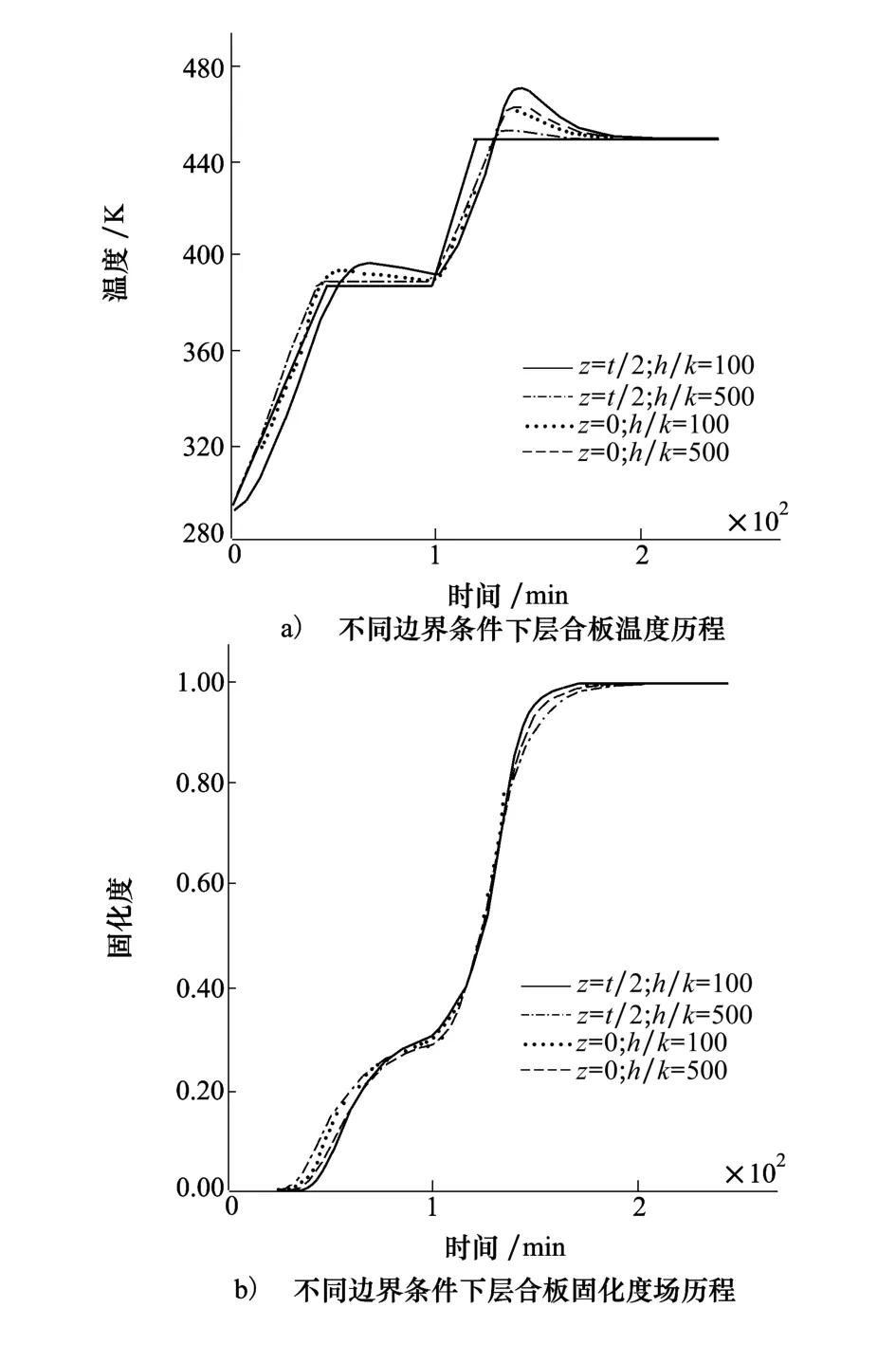
图4 边界条件对AS4/3501-6层合板温度、固化度的影响
图4a)给出了层合板表层(z=0)中心点和中间层(z=t/2)的中心点温度曲线,由计算结果可知:随着h/k比值的增大,层合板升温速率加快,中心点温度峰值逐渐减小。图4b)是对应条件下的固化度曲线,结果表明h/k越小,放热期间固化度梯度将会增加。
4.2 厚度的影响
对于前述AS4/3501-6层合板,取1.27 cm、2.54 cm、3.81 cm 3种不同厚度,上下表面为第1类边界条件,侧面为绝热边界。图5a)和图5b)为这3种不同厚度层合板固化过程中心点的温度和固化度变化历程。由图5a)的温度曲线可知,在中心点温度超过保温平台温度之前,1.27 cm层合板的温度最高,2.54 cm板次之,3.81 cm板温度最小,超过保温平台温度最晚,但温度峰值明显高于其他2个。由图5b)的固化度曲线可知,1.27 cm层合板固化反应启动时间最早,进行时间最长,而3.81 cm层合板固化反应启动最晚,但最先结束。所以厚度越大,中心点温度峰值就出现得越晚,峰值越大,中心点固化开始得就越晚,而完成固化所需时间就越短。
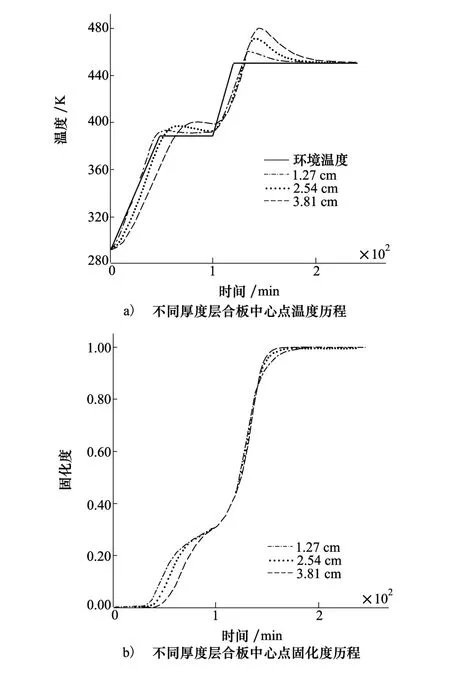
图5 厚度对AS4/3501-6层合板温度、固化度的影响
4.3升温速率的影响
对于前面所述AS4/3501-6层合板,上下表面采用第1类边界条件,侧面为绝热边界,层合板在389 K温度下固化60 min后,再分别施以1.5 K/min,3 K/min和6 K/min的加热速率达到449 K。
图6a)和图6b)分别给出了不同升温速率下,层板中心点温度和固化度随时间的变化曲线。由图6a)可知,升温速率越慢,中心点温度升温越慢,峰值越小,峰值过后的降温过程也越慢;同时由图6b)可知,升温速率越慢,固化速率越慢,固化完成所需时间也越长。
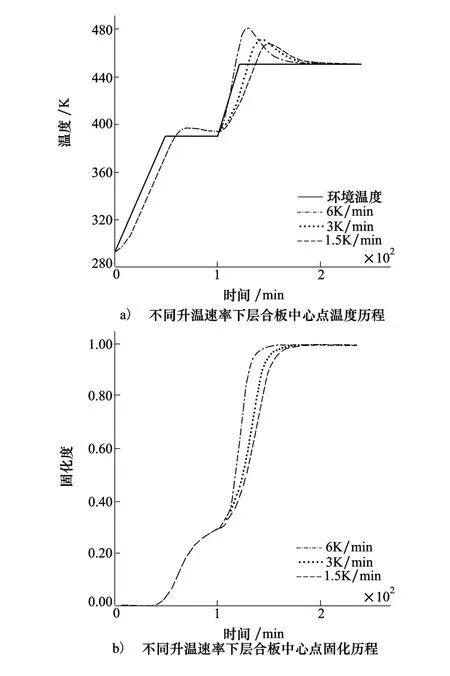
图6 升温速率对AS4/3501-6层合板温度、固化度的影响
5 结 论
1)根据热传导和唯象固化动力学理论,建立了正交各向异性复合材料层合板固化过程的三维有限元模型;研究了基于ABAQUS子程序耦合求解温度场和固化度场的方法,通过对比算例与文献实验结果,验证了本文方法的正确性。
2)由边界条件对温度场和固化度场的影响表明,h/k越大,层合板升温越快,中心点温度峰值越小,放热期间固化度梯度减小,因而h/k的增大有利于减轻温度场和固化度场的不均匀性。
3)由厚度对温度场和固化度场的影响表明,层板越厚,固化开始得越晚,中心点温度超过保温平台温度越晚,温度峰值越大,完成固化所需时间越短。
4)升温速率对温度场和固化度场的影响表明,升温速率越慢,中心点温度升温越慢,峰值越小,降温过程也越慢,从而降低了固化速率,使得固化完成所需时间延长,因而适当降低升温速率有利于减轻温度场和固化度场的不均匀性,但同时也会延长固化完成时间,二者之间要根据实际情况权衡。
5)本文基于ABAQUS子程序所建立的复合材料三维有限元固化数值模拟方法,适用于模拟具有不同类型动力学方程的复合材料固化过程,可分析复杂形状和边界条件下结构固化过程温度场和固化度场,因此对改善固化工艺参数具有一定的指导意义。
参考文献:
[1] Wang J,Kelly D.Finite Element Analysis of Temperature Induced Stresses and Deformations of Polymer Composite Components [J].Journal of Composite Materials,2000,34(17):1456-1471
[2] Loos A C,Springer G S.Curing of Epoxy Matrix Composites[J].Journal of Composite Materials,1983,17(2):135-169
[3] Bogetti T A,Gillespie J W.Two Dimensional Cure Simulation of Thick Thermosetting Composite[J].Journal of Composite Materials,1991,25(3):239-250
[4] 杨正林,陈浩然.层合板在固化过程中瞬态温度场及固化度的有限元分析[J].玻璃钢/复合材料,1997(3):3-7
Yang Zhenglin,Chen Haoran.The Finite Element Analysis of Transient Fields of the Temperature and Degree of Cure of Laminates during the Whole Curing Process[J].Fiber Reinforced Plastics/Composites,1997(3):3-7(in Chinese)
[5] Cheung A,Yu Y,Pochiraju K.Three-Dimensional Finite Element Simulation of Curing of Polymer Composites[J].Finite Elements in Analysis&Design,2004,40(8):895-912
[6] 张纪奎,郦正能,关志东,等.热固性复合材料固化过程三维有限元模拟和变形预测[J].复合材料学报,2009,26(1):174-178
Zhang Jikui,Li Zhengneng,Guan Zhidong,et al.Three-Dimensional Finite Element Simulation and Prediction for Process-Induced Deformation of Thermoset Composites[J].Acta Material Compositae Sinice,2009,26(1):174-178(in Chinese)
[7] Boey Fyc,Song Xl,Yue Cy,et al.Modeling the Curing Kinetics for a Modified Bismaleimide Resin[J].Journal of Polymer Science Part A:Polymer Chemistry,2000,38(5):907-913
[8] Park H C,Lee S W.Cure Simulation of Thick Composite Structures Using the Finite Element Method[J].Journal of Composite Materials,2001,35(3):188-201
Finite Element Analysis for Curing Process of Composite Laminates
Peng Liang,Mao Wei,Zhao Meiying
(College of Aeronautics,Northwestern Polytechnical University,Xi′an 710072 China)
In this paper,three-dimensional numerical simulation of the curing process of composite laminates is realized with ABAQUS subroutine secondary development method.Being verified by two examples,this method can predict coupled temperature field and degree of cure field relative precisely in the curing process.Moreover,the influence of boundary conditions,thickness and heating rate on the temperature field and the degree of cure field are discussed with this method.When curing kinetic equations are different for different types of composites,just program with the Fortran language on the basis of ABAQUS subroutine according to the corresponding equations;this shortens the program cycle.The applicability of this method is universal and it provides meaningful guidelines to refine the curing process parameters.
curing process;boundary condition,ABAQUS,finite element method,subroutine,heating rate,temperature distribution
V258
A
1000-2758(2015)06-0900-06
2015-04-28基金项目:国家自然科学基金(11502205)资助
彭亮(1982—)西北工业大学讲师、博士研究生,主要从事飞行器设计与适航研究。
