基于对偶分解的分布式协同编队飞行研究

过娟，褚晶，闫杰

（1.西北工业大学航天学院，陕西西安 710072；2.西北工业大学航空学院，陕西西安 710072）

基于对偶分解的分布式协同编队飞行研究

过娟1，褚晶2，闫杰1

（1.西北工业大学航天学院，陕西西安 710072；2.西北工业大学航空学院，陕西西安 710072）

针对多智能体编队飞行问题，提出一种新的基于对偶分解的分布式算法，以实现协同航迹规划。首先，将编队飞行问题建模为受线性动力学约束的优化问题，其目标函数中包括智能体各自的独立目标（例如跟踪参考轨迹）以及系统的全局目标（例如总燃料消耗、编队队形等）。其次，为了分布式地求解该优化问题，将其对偶问题分解，把大计算量的原问题转化为多个小的子问题。最后，设计了协同分布式规划算法，并对其收敛性和最优性进行了理论证明。由于该算法只需相邻智能体间的通信，因此具有很强的可扩展性，并能适用于通信能力受限情况下的编队飞行。仿真结果表明，提出的分布式算法能有效地进行协同编队飞行规划；同时通过与集中式方法的比较，其最优性和收敛性得到了验证。

分布式优化；对偶分解；编队飞行；协同智能体

小型无人驾驶飞行器（unmanned aerial vehicle，UAV）凭借其自身成本低、重量轻、体积小、操作灵活等诸多优点，在军事以及民用领域有着越来越广泛的运用。然而，由于单个小型无人机的能力有限，使其难以满足日益复杂的应用要求，因此，多小型无人机通常采用协同编队飞行的方式完成所设计的任务，例如灾后进行区域内的协同搜索［1］，森林的火灾巡逻、预警［2］等。在多无人机系统中，为减轻地面站的负担，降低操作成本，增加系统的灵活性、可靠性、可扩展性以及鲁棒性，通常将无人机设计为协同合作的智能体自主地完成机上的各种操作，而无须时刻接收地面站发送的指令。在众多自主操作中，编队飞行的协同轨迹规划是多无人机系统完成设计任务的前提［3］。

目前文献中的研究主要是针对单个UAV的航迹规划［4］、多个UAV的集中式编队飞行航迹规划［3］以及多个UAV的混合式编队飞行航迹规划［2］。其中，集中式编队飞行规划是指编队中的某一UAV先接收系统中所有UAV的信息，然后运行规划算法，最后将生成的结果发送给其他UAV；而分布式协同规划需要系统中所有UAV都承担部分规划计算任务，且计算过程中只需要其邻居UAV的相关信息；混合式协同编队规划则介于集中式与分布式规划之间。综上所述，集中式编队飞行规划对UAV间的通信拓扑结构有严格的要求（需要多点对单点的通信结构），存在着单点脆弱性、扩展性差的缺点，不适于数目较多的多UAV系统（因为规划问题的复杂度随着UAV个数的增多而显著增加，计算量也因此加大）。虽然混合式编队规划算法部分弥补了集中式算法的不足，但它依然要求多点对单点的通信结构，且存在单点脆弱性。

对于小型UAV，其通信能力会受到平台大小的制约，因此需要开发仅需要相邻UAV信息的分布式算法。本文基于对偶分解原理，提出了一种新的分布式算法以实现多智能体编队飞行的协同航迹规划，给出了规划的优化模型，进行了对偶分解的详细推导，分析了所设计方法的最优性和收敛性，并完成了以5个智能体进行V字形协同编队飞行的仿真验证。

1　多智能体协同编队飞行的优化模型

在本文的研究中，假设协同编队飞行中的每个智能体都受到线性动力学的约束；在航迹规划中，它们既要完成各自任务也要完成系统的全局任务。在本文提出的协同编队飞行的优化模型中，首先将线性动力学约束转化为关于决策变量的线性等式约束，然后使用目标函数描述智能体的独立任务以及系统的全局任务。

1.1线性动力学约束

假设协同编队飞行中有n个智能体，且每个智能体的动力学模型表示为：

式中，xi为第i个智能体的状态变量，ui为其控制输入，Aic和Bic分别是其系统矩阵和输入矩阵。对于线性动力学系统，可以使用离散化的方法对其进行求解［5］：

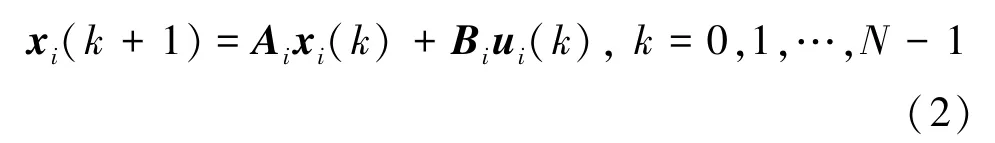
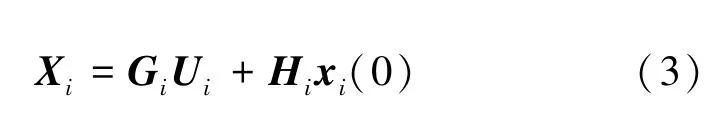
式中

（3）式建立了智能体i各个时刻的状态变量与其控制变量之间的线性关系。在协同编队飞行中，通常希望智能体在某时刻能够实现特定的状态目标；借助于（3）式，该状态目标即可转化为关于Ui的表达式。

1.2智能体的独立目标

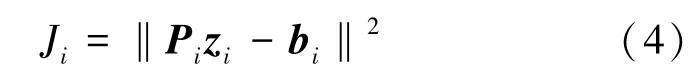
式中，‖·‖表示向量的2范数。每个智能体的独立目标就是要最小化Ji。

1.3系统的全局目标

在本文的研究中，协同编队飞行系统的全局目标主要包括所有智能体的燃料消耗总和最小以及相邻智能体位置之间保持特定的队形。燃料消耗总和最小可以表示为：

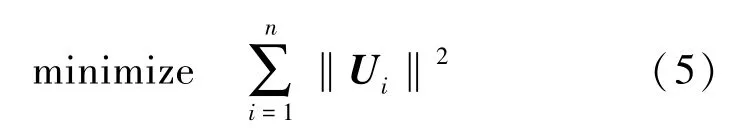
相邻智能体之间的位置保持特定队形可以表示为：

式中，Ni为与智能体i相邻的智能体集合，δij为智能体i和j之间设定的位置队形。

1.4优化模型

结合（3）式～（6）式，受线性动力学约束的协同编队飞行可以建模为以下的优化问题：

subject to Xi=GiUi+Hixi（0），i=1，…，n优化问题（7）的优化变量为zi，i=1，2，…，n。

在优化问题（7）中，目标函数包括智能体各自独立的目标以及系统的全局目标，约束则由智能体的线性动力学约束构成。由于目标函数是二次型多项式且约束为线性等式约束，因此优化问题（7）是一个凸优化问题［7］。

2　对偶分解

运用对偶分解分布式地求解优化问题（7）就是要将原来包含所有智能体变量的大型、非线性问题分解成一系列较小的问题进行求解；且每个小问题只与一个独立智能体相关，并只包含这个智能体的变量。因此，原问题便可以被分配到每个智能体上求解，这就构成了分布式算法。然而，优化问题（7）的目标函数不具备可分解的形式，首先需要对其进行解耦操作。

2.1解耦目标函数

优化问题（7）的目标函数中，第1个求和符号里的求和项是解耦的，但第2个求和符号中的Xi会出现在不同的非线性求和项中，因此求和项之间是耦合的，需要进行解耦操作。解耦的目的即建立一个与问题（7）等价的新问题，且在求和符号中的不同非线性求和项中不存在相同的优化变量，从而便于进行对偶分解。为此，为每个智能体引入松弛变量，将问题（7）转化为：引入松弛变量后，优化问题（8）的目标函数是解耦的。显而易见，优化问题（8）与问题（7）等价，也是凸优化问题。问题（8）中的可以理解为智能体Xij获得的相邻智能体j的状态信息。

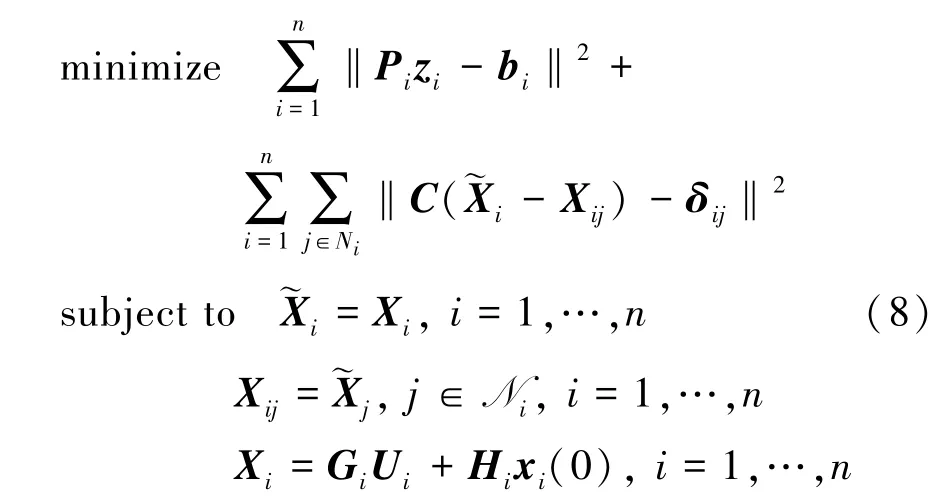
2.2具备可分解形式的对偶问题

为设计分布式算法，需要将优化问题（8）分解为一系列可由智能体独立求解的小问题。然而，优化问题（8）的原始形式不便于分解。但由于优化问题（8）是凸优化问题，具备强对偶性，因此它的解可以通过求解其对偶问题获得。经过下面的推导，可以看出优化问题（8）的对偶问题具备可分解的形式。然而，为求得优化问题（8）的对偶问题，首先要推导出它的拉格朗日函数，接着再求出它的对偶函数。

优化问题（8）的部分拉格朗日函数为：

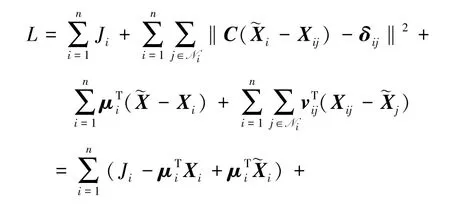
式中，μi是与等式约束对应的拉格朗日乘子向量，而vij是与等式约束对应的拉格朗日乘子向量。由（9）式可以看出，引入松弛变量后，优化问题（8）的部分拉格朗日函数L是解耦的。因此，相关的对偶函数也是解耦的。优化问题（8）的对偶函数为：

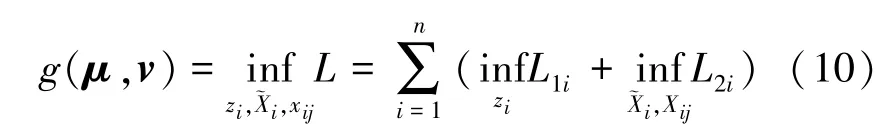
式中，μ是由所有μi（i=1，2，…，n）构成的向量，v是由所有构成的向量，L1i=且

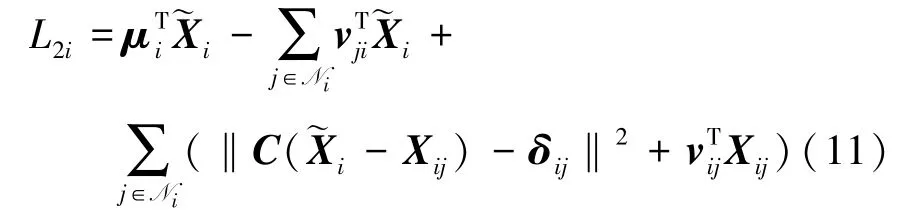
当智能体的独立目标为跟踪参考轨迹，而系统的全局目标包含总燃料消耗最小时，可以根据L1i的最小值推导出最优控制和最优轨迹的表达式。将（3）式代入L1i得到：

式中

为求L1i的最小值，应使下式成立：

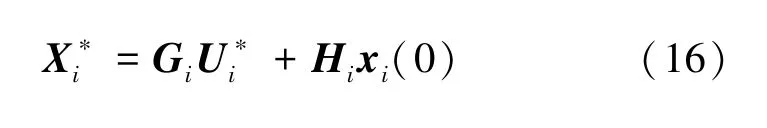
结合（15）式和（16）式，L1i的最小值为

L2i关于以及Xij的最小值推导如下。首先，L2i相对于以及Xij的偏导数应满足：

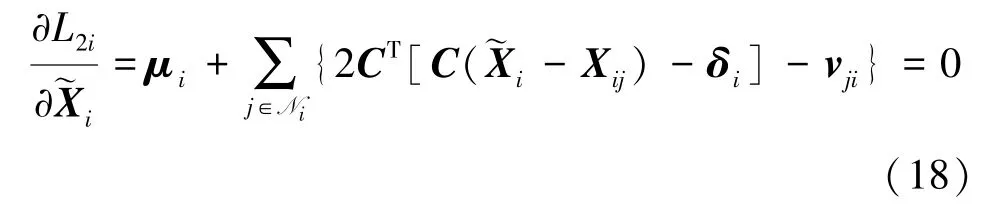
以及

联立（18）式和（19）式可以得到如下重要的关系式：

将（20）式代入（11）式有：

由（21）式可知，L2i是关于的一个二次函数，其最小值为：

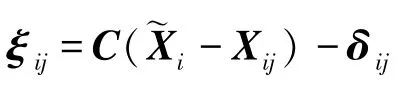
将（23）式代入（22）式，L2i的最小值变为

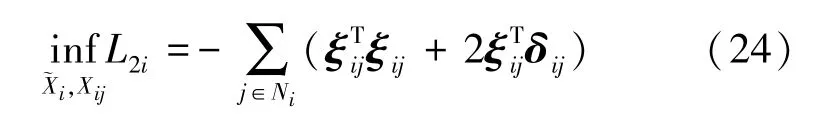
结合（23）式和（20）式，L1i的最小值也可由编队飞行的队形品质ξij表示：

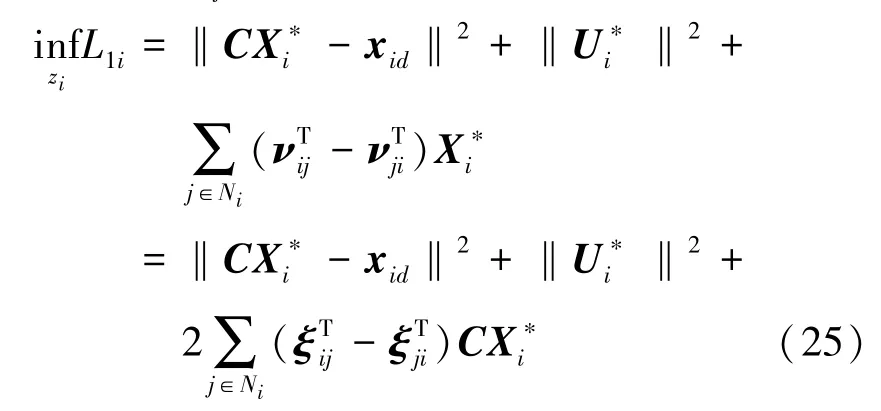
将（24）式和（25）式代入（10）式，优化问题（8）式的对偶函数变为一个关于编队飞行队形品质的函数：

式中，ξ是由所有ξij（i=1，2，…，n，j∈Ni）构成的向量。

至此，优化问题（8）式的对偶问题可描述为：

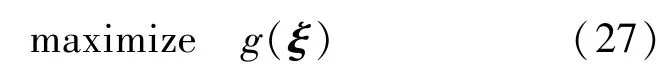
显而易见，结合（26）式，对偶问题（27）式相对于ξij具备可分解的形式。因此，分布式地求解问题（27）式便可以获得优化问题（8）式的解。

2.3对偶问题的求解

在本文的研究中，运用次梯度方法求解对偶问题（7）［8］。由于次梯度方法只适用于求解函数的最小值，故将对偶问题（7）转化为求解-g（ξ）的最小值。函数-g（ξ）相对于ξij的一个次梯度可表示为：

运用次梯度方法，ξij的迭代公式如下：

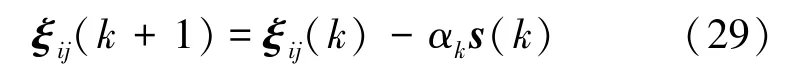
式中，ξij（k）为ξij第k次迭代时的值，αk为第k次迭代时的迭代步长，s（k）为第k次迭代时次梯度的值，即：

一般情况下，迭代步长αk有5种选取准则［8］。①定步长，即αk=α，α为正常数。②定间隔，即每次迭代中ξij前后差值的模为常数。例如，αk= γ/‖s（k）‖2，式中γ为正常数。③步长平方可加但步长不可加，例如αk=a/（b+k），式中a为正数，b为非负数。④步长不可加而步长递减，例如αk=a/，式中a为正数。⑤间隔不可加而间隔递减，例如。前2种步长选取准则只能保证次梯度算法收敛到最优值的某个邻域，而后3种准则能确保次梯度算法收敛于最优值。

3　分布式协同算法

3.1算法的描述

在上一节推导的基础上，可以设计出适用于多智能体协同编队飞行的分布式算法。该算法总结如下。

2）智能体i根据（3）式计算νij（k）和νji（k），并根据（20）式计算μi（k）；

5）智能体i根据（9）式计算ξji（k+1）以更新编队飞行品质。

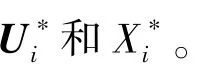
以上的分布式算法可以有如下直观的解释。首先，每个智能体先忽略系统的全局目标，只基于各自的局部目标计算最优轨迹。接着，每个智能体将自己的最优轨迹信息发送给那些与它在全局目标中相关联的智能体；与此同时，也接收来自于这些智能体的最优轨迹信息。在交换轨迹信息之后，每个智能体开始计算它与全局目标的偏离量，再基于偏移量计算出新的最优轨迹。重复以上过程直至与全局目标的偏离量收敛。

在本文设计的分布式算法中，一共存在两次信息交互的过程。第一次是交互编队飞行品质信息；第二次是交互最优轨迹信息。两次信息的交互都只发生在相邻的智能体之间，因此对系统的通信拓扑结构没有苛刻的要求。

3.2算法的最优性

本文提出的分布式算法采用次梯度方法求解优化问题（8）的对偶问题（27）。由于优化问题（8）是一个凸优化问题，对于有可行解的协同编队飞行问题（意味着满足Slater条件），根据凸优化理论，优化问题（8）具有强对偶性［7］。因此，由对偶问题（27）的最优解能得到优化问题（8）的最优解；又由于最优问题（8）和问题（7）等价，故分布式算法能给出协同编队飞行问题的最优解。

3.3算法的收敛性［8］

分布式算法的收敛性取决于运用次梯度方法求解对偶问题（27）的收敛性。令f（ξ）=-g（ξ），则要说明次梯度方法的收敛性就是要比较迭代值f（ξk）（ξk为第k次迭代时向量ξ的值）与最优值f（ξ∗）（ξ∗为f（ξ）取得最优值时向量ξ的值）之间的关系。首先，根据迭代公式，有以下关系式成立：

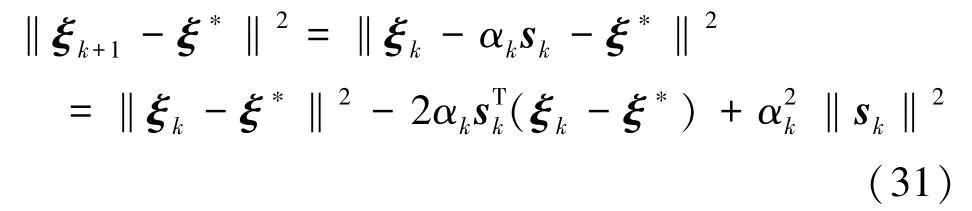
根据次梯度的定义有［8］：

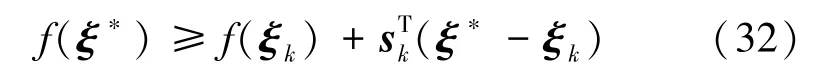
将不等（32）式代入（31）式中，得到：

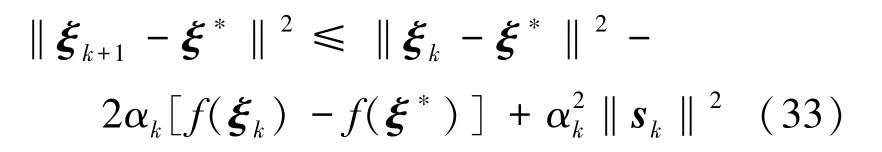
重复运用不等关系式（33），得到：

令‖ξ0-ξ∗‖2≤R，即初始值ξ0选取在ξ的有界值域内，则有：

令fbest是迭代过程中使得f（ξi）-f（ξ∗），i=0，1，…，k，最小的函数值，则：

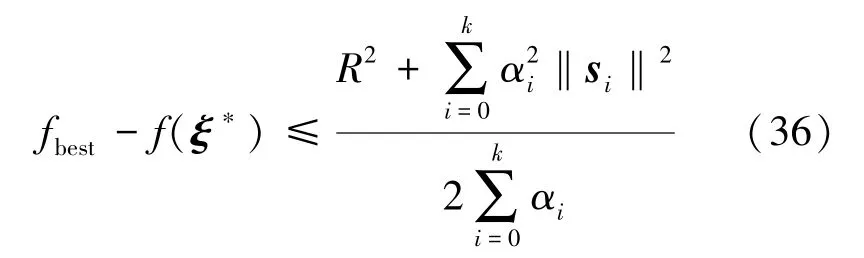
由（26）式可以看出：f（ξ）是一个关于ξ的二次函数，因此满足Lipschitz条件，即

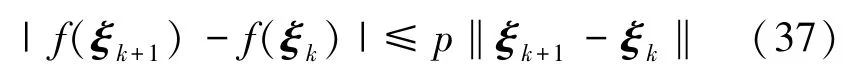
结合不等（37）式、（32）和（36）式，有

如果迭代步长的选取准则为步长平方可加但步长不可加，即

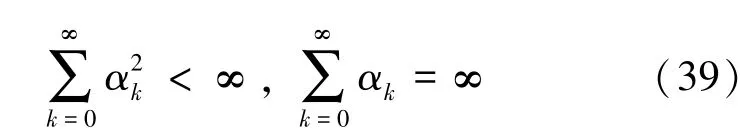
4　仿真与分析

为验证上述分布式算法的可行性、最优性以及收敛性，这里以5个智能体的V字形协同编队飞行为例进行仿真分析。V字形协同编队飞行如图1所示：图1中也给出了的定义。V字形协同编队飞行可以由两智能体间的距离以及夹角θ描述。在仿真中，将相邻智能体之间的距离设置为等距200 m，且θ=60°。

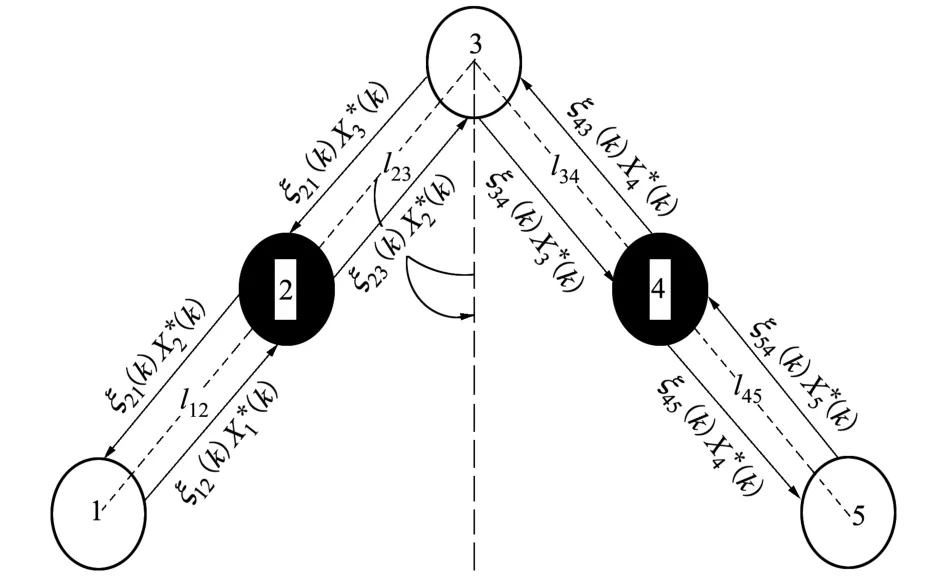
图1　包含5个智能体的V字形协同编队飞行

编队中每个智能体的系统矩阵和输出矩阵都分别设置为：

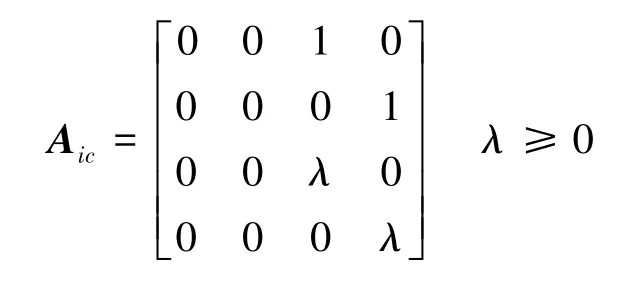
在后面的仿真算例中，将λ设为0。智能体的初始状态为（位置单位为km，速度单位为km/s）：

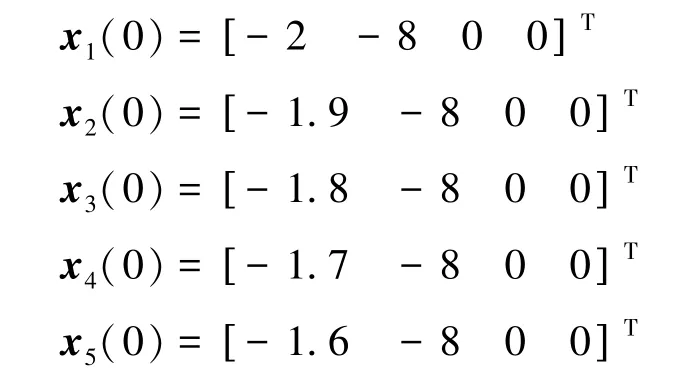
即初始时刻5个智能体两两相距100 m一字排开。每个智能体跟踪的参考轨迹相同：该参考轨迹为三次曲线y=x3，且x∈［-2 km，2 km］，如图2中虚线所示。在仿真中，初始时刻设为0时刻，编队飞行的总时间为50 s，离散化步长为1 s。而在分布式算法的初始输入中，都设为0向量。

对于以上设定的仿真场景，本文先设计了集中算法对其进行求解，即对问题（7）直接求解。由于问题（7）是凸优化问题，可以用开源的凸优化求解器进行求解。本文使用的是CVX求解器［9-10］。在求解问题（7）的过程中，需要将所有智能体的状态信息发送给进行计算的智能体，因此是集中式算法。集中式算法的结果由图2中的“+”标记。最终集中式算法给出的目标函数最小值为14.346 4。将集中式算法的结果作为分布式算法的参照。分布式算法给出的优化轨迹如图2中“o”标记的点所示，其结果与集中式算法给出的结果一致。最终时刻协同编队飞行的构型如图3所示。

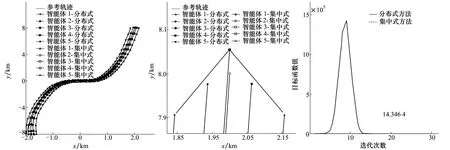
图2　协同编队飞行轨迹优化仿真结果 图3　编队飞行50秒时刻的构型 图4　分布式算法中目标函数值的迭代结果

这里需要说明的是：由于在目标函数中同时考虑了智能体各自独立的目标以及系统的全局目标，最终时刻每个智能体的轨迹并没有完全跟踪参考轨迹，而最终构型也不是预先设定的V字形编队。这是因为仿真的最优结果是智能体各自独立目标与系统全局目标之间的一个妥协。

分布式算法中目标函数值的迭代结果如图4所示（本文的迭代步长选为αk=1/k）。在图4中，目标函数的值先增大再减小，最终收敛于最优值。从图4可以看出，次梯度方法并不像传统的梯度下降法那样使目标函数值一直减小。在本文的仿真设定下，分布式算法只需迭代14次便收敛于最优值14.346 4。

5　结 论

为了解决通信能力受限情况下的协同编队规划问题，文中提出了一种基于对偶分解方法的分布式算法，不仅能快速地收敛于全局最优值，而且只需较少的通信信息。在设计的分布式算法中，每一次迭代过程仅需相邻智能体间进行两次通信，且通信量较小（仅包括编队飞行品质和当前的最优轨迹）。文中将协同编队飞行建模为受动力学约束的优化问题，且在目标函数中考虑智能体各自独立的目标和系统的全局目标；这种建模方法有利于推导出对偶分解的基本形式。除此之外，将对偶分解和次梯度方法结合求解协同编队飞行规划问题，能够充分利用凸优化已有的理论结果对设计的分布式算法进行最优性以及收敛性证明。未来将考虑更为复杂的动力学约束和控制约束进行协同编队飞行的分布式路径规划。

［1］ 彭辉，沈林成，朱华勇.基于分布式模型预测控制的多UAV协同区域搜索［J］.航空学报，2010，31（3）：593-601

Peng Hui，Shen Lincheng，Zhu Huayong.Multiple UAV Cooperative Area Search Based on Distributed Model Predictive Control ［J］.Acta Aeronautica et Astronautica Sinica，2010，31（3）：593-601（in Chinese）

［2］ 李远.多UAV协同任务资源分配与编队轨迹优化方法研究［D］.长沙：国防科技大学，2011

Li Yuan.Research on Resources Allocation and Formation Trajectories Optimization for Multiple UAVs Cooperation Mission［D］. Changsha，National University of Defense Technology，2011（in Chinese）

［3］ 白瑞光，孙鑫，陈秋双，等.基于Gauss伪谱法的多UAV协同航迹规划［J］.宇航学报，2014，35（9）：1022-1029

Bai Ruiguang，Sun Xin，Chen Qiushuang，et al.Multiple UAV Cooperative Trajectory Planning Based on Gauss Pseudospectral Method［J］.Journal of Astronautics，2014，35（9）：1022-1029（in Chinese）

［4］ 傅阳光，周成平，王长青，等.考虑时间约束的无人飞行器航迹规划［J］.宇航学报，2011，32（4）：749-755

Fu Yangguang，Zhou Chengping，Wang Changqing，et al.Path Planning for UAV Considering Time Constraint［J］.Journal of Astronautics，2011，32（4）：749-755（in Chinese）

［5］ 郑大钟.线性系统理论［M］.北京：清华大学出版社，2005

Zheng Dazhong.Theory of Linear Systems［M］.Beijing，Tsinghua Press，2005（in Chinese）

［6］ Raffard R L，Tomlin C J，Boyd S P.Distributed Optimization for Cooperative Agents：Application to Formation Flight［C］∥43rd IEEE Conference on Decision and Control，2004：2453-2459

［7］ Boyd S，Vandenberghe L.Convex optimization［M］.London，Cambridge University Press，2004

［8］ Michael C，Stephen P.Graph Implementations for Nonsmooth Convex Programs［J］.Recent Advances in Learning and Control，2008，371：95-110

Distributed Cooperative Planning of Formation Flying Based on Dual Decomposition

Guo Juan1，Chu Jing2，Yan Jie1
1.College of Astronautics，Northwestern Polytechnical University，Xi′an 710072，China 2.College of Aeronautics，Northwestern Polytechnical University，Xi′an 710072，China

This paper presents a distributed algorithm to address the cooperative planning of multiple agents flying in formation.First，the cooperative trajectory planning subject to linear dynamics constraints is formulated as an optimization problem，where the objective includes not only private（such as tracking reference trajectories）but also common（such as overall fuel consumption，formation and so on）goals for all agents.Second，in order to solve the optimization problem in a distributed fashion，the dual decomposition technique is employed to replace the original complex problem of very high computational load by multiple smaller sub-problems，which are then distributed over agents.Last but not least，a distributed algorithm is developed to solve the dual problem and thus the original cooperative planning problem because there is no duality gap due to the convexity of the problem.Since the algorithm only requires neighbors′information，it is scalable and applicable when the communication capabilities are limited. Simulation results show the efficiency and efficacy of the algorithm when applied to the cooperative planning of formation flying.Meanwhile，as compared with the centralized method，the optimality and convergence of the algorithm are demonstrated as well.

algorithms，computer simulation，convergence of numerical methods，convex optimization，dynamics，efficiency，fuel consumption，matrix algebra，optimization，scalability，trajectories，vectors；cooperative agents，distributed optimization，dual decomposition，formation flying

TP391

A

1000-2758（2015）06-0892-08

2015-04-01

过娟（1986—），女，西北工业大学博士研究生，主要从事分布式优化及制导技术的研究。