多险种多复合Poisson-Geometric过程的常利率风险模型

李碧云，余国胜

（江汉大学数学与计算机科学学院，湖北 武汉 430056）

0 引言

文献［1]中首先引入一类称为Poisson-Geometric过程的计数过程，作为索赔次数过程它是Poisson过程的一种推广，而且有着实际的应用背景.近年来，Poisson-Geometric过程的研究受到许多学者的广泛关注.文献［1]中在没有考虑利率因素的条件下，得到了破产概率公式及更新方程.文献［2]中求出了Gerber-Shiu折现罚金函数所满足的更新方程及破产概率的Pollazek-Khinchin公式.现实生活中风险模型往往是带有利率的，引入利率以加强模型的现实描述能力，是当前精算学研究的热点之一.熊双平［3]将文献［1]中的结果推广到常利率复合Poisson-Geometric风险模型.但是所研究的险种是单一的.然而，随着保险公司经营规模的不断扩大以及新险种的开发，用此风险模型来描述风险经营过程就具有一定的局限性.赵金娥等［4-5]建立了索赔次数为复合Poisson-Geometric过程的双险种风险模型，给出初始盈余为0时破产概率的具体表达式，并得到在初始盈余为u时破产概率的近似估计及指数分布下的表达式.并考虑了保费收入为复合Poisson过程且索赔次数为复合Poisson-Geometric过程的双风险模型，给出了生存概率满足的积分方程及其在指数分布下的具体表达式，并应用鞅方法得到了最终破产概率满足的一般公式和Lundberg不等式，同时导出有限时间内生存概率的积分-微分方程.所考虑的模型不带利率，单位时间未收到保单.笔者在此基础上研究了多险种多复合Poisson-Geometric过程的常利率风险模型的生存概率，得到该模型的生存概率所满足的积分-微分方程.当无保费收入时，由所得到的积分-微分方程推出生存概率的Laplace变换的表达式，对于初始盈余为0时，得到生存概率的精确解，并给出具体的数值计算的实例以解释我们的结果.

1 模型引入

定义1.1设(Ω,F,P)是一个完备的概率空间，本文中所有的随机变量都定义在这个空间上，则对初始盈余u≥0,t≥0,定义保险公司在t时刻的盈余为：

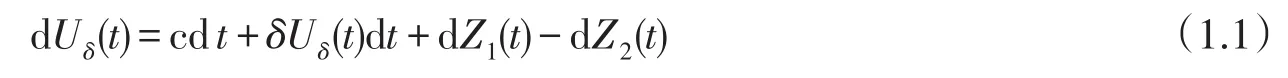
其中

它们是一个随机过程，分别称为保费收入过程和理赔过程，N1(t),N2(t),…,Nm(t)分别为到t时刻为止m种保单个数分别为第i(i=1,2,…,m)种保单第k次收取的保费，其均为均值为μ1,μ2,…,μm的独立同分布非负随机变量序列.它们的分布函数分别为FX1(x),FX2(x),…,FXm(x),相应的密度函数为为FX1(x),FX2(x),…,FXm(x)的k重卷积，相应的密度函数为t时刻为止n-m险种理赔次数分别记为Nm+1(t),Nm+2(t),…,Nn(t)，而分别为第i(i=1,2,…,n-m)种险种第k次的理赔额.其均为均值为μm+1,μm+2,…,μn独立同分布非负随机变量序列，其分布函数分别为FY1(y),FY2(y),…,FYn-m(y),密度函数为fY1(x),fY2(x),…,fYn-m(x),且分别为FY1(x),FY2(y),…,FYn-m(x)的k重卷积，相应的密度函数为所有保费与理赔额同N1(t),N2(t),…,Nn(t)相互独立，且

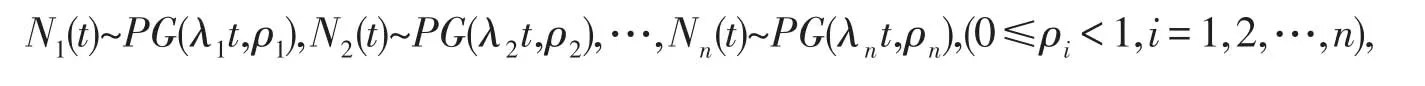
此模型称为常利率多险种多复合Poisson-Geometric风险模型.

由（1.1）式可知：

其中

定义1.2记T=inf{t≥0,Uδ(t)＜0},表示保险公司破产时刻(T=∞时，可以认为∀t≥0均有Uδ(t)≥0,即破产不会发生），则在初始盈余为u的条件下，定义保险公司的最终破产概率为φδ(u)=Pr{T＜∞|U(0)=u},ψδ(u)=1-φδ(u)为生存概率.

为保证保险公司的安全运作，通常要求

2 预备知识及引理

以下考虑在常数利率δ下多险种多复合Poisson-Geometric风险模型，为此先给出Poisson-Geometric过程的定义如下：

定义2.1称母函数为所对应的分布为复合 Poisson-Geometric 分布，记为PG(λt,ρ),其中λ＞0,0≤ρ＜1.

定义2.2设λ＞0,0≤ρ＜1,称{N(t);t≥0}为参数λ,ρ复合Poisson-Geometric过程，如果满足：

（i）N(t)=0 ；

（ii）{N(t);t≥0}具有平稳独立增量；

（iii）对t＞0 ，有N(t)～PG(λt)而且

注2.1 由定义2，当ρ=0时，复合Poisson-Geometric过程就是Poisson过程.因此，复合Poisson-Geometric过程是Poisson过程的一种推广.

与文献［4]中引理1，引理2的证明方法类似可得：

引理2.1

引理2.2

引理 2.3[1]设 {Ni(t),t≥0}是参数为 (λi,ρi)(i=1,2,…,n)复合Poisson-Geometric过程时，αi=λi=αiρi,i=1,2,…,n),则当t足够小时有

3 ψδ(u)的更新方程

定理3.1记

则模型（1.1）的生存概率满足更新方程

定理3.1的证明对充分小的h，考察(0,h]内的盈余过程，由全概率公式及引理得

经整理，得

上式两边同除以h，令h→0,而0≤ρi＜1(i=1,2,…,n),再由引理2.3知，

均一致收敛，由单调收敛定理知∫与∑交换次序无问题，所以

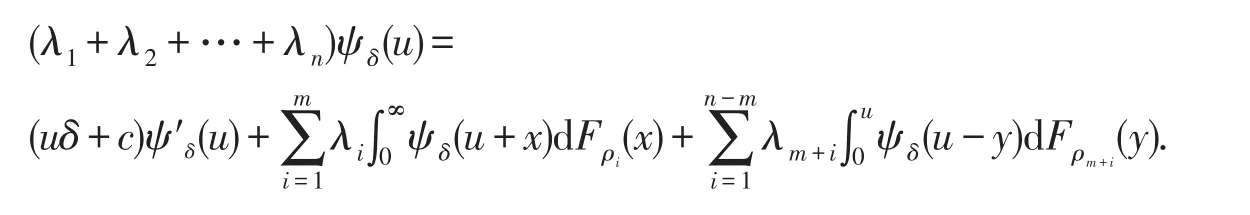
注3.1 当δ=0,m=0,n=2,则（3.1）式为文献［4]中的（1）式.

注3.2 当δ=0,c=0,m=1,ρ1=0,n=3,则（3.1）式为文献［5]中的定理（1）.

（3.1）式从0到u积分，则有

推论3.1

4 ψδ(0)的精确解和ψδ(u)的Lap lace变换的表达式

为了计算的方便，作辅助函数

其中Zδ∗F*ρm+i是Zδ和F*ρm+i

的Stieltjes卷积.

引入函数Zδ(x)的Laplace-Stieltjes变换：

对（4.1）式两边取Laplace-Stieltjes变换并整理可得

一般来讲，很难给出ψδ(u)的Laplace变换的精确解，但是当无保费收入时，可以得到ψδ(0)的精确解和ψδ(u)的Laplace变换的表达式.

由（4.2）式有

令

（4.3）式即为

当δ＞0时，有

从s到∞积分化简得

将（4.4），（4.5）式代入（4.7）式计算可得

注意到γδ(0)=1，则有

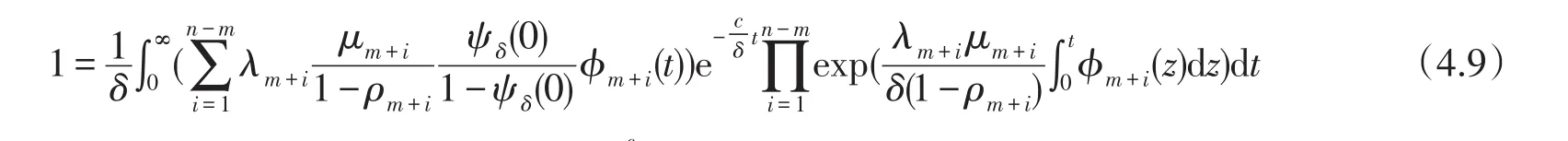
令

为了说明结果的有效性，我们举一个实例.

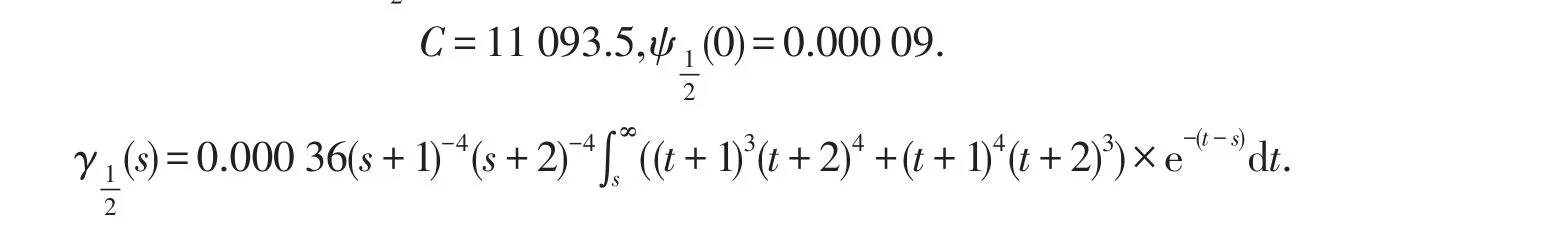
［1]毛泽春，刘锦萼.索赔次数为复合Poisson-Geometric过程的风险模型及破产概率［J].应用数学学报，2005，28（3）：419-428.

［2]廖基定，龚日朝，刘再明.复合Poisson-Geometric风险模型Gerber-Shiu折现惩罚函数［J].应用数学学报，2007，30（6）：1076-1085.

［3]熊双平.索赔次数为复合Poisson-Geometric过程的常利率风险模型的罚金函数［J].经济数学，2008，25（2）：136-142.

［4]赵金娥，王贵红，龙瑶.一类双险种风险模型的破产概率［J].西南师范大学学报：自然科学版，2013，38（1）：16-21.

［5]赵金娥，王贵红，龙瑶.索赔次数为复合Poisson-Geometric过程的双险种风险模型［J].经济数学，2012，29（1）：79-84.

［6]Grandeii.Aspectsof risk theory［M].New York：Springer-Verlag，1991.