(α,β)混合序列部分和与乘积和的强大数定律

赵琦

（湖北大学数学与统计学学院，湖北 武汉 430062）

0 引言

设{Xn,n≥1}为定义在概率空间(Ω,F,P)上的随机变量序列.记设n和m为正整数，记在F中给定σ域B和R，令

(α,β)混合序列的定义由Bradley[1]给出，由 (α,β)的定义可知 (α,β)混合序列是包含独立序列的一类非常广泛的序列.Bradley研究了绝对正则条件下(α,β)混合序列的中心极限定理.邵启满[2]研究了(α,β)混合序列的极限定理.陆传荣和林正炎[3]于1997年建立了(α,β)混合序列协方差的界，沈燕[4]给出了(α,β)混合序列的Kolmogorov不等式，得到 (α,β)混合序列的收敛定理.本文中利用此不等式得到 (α,β)混合序列的三级数定理，在较弱的条件下，进一步研究了(α,β)混合序列部分和与乘积和的强大数定律.

1 预备知识

引理 1[3]设 {Xn,n≥1}为 (α,β)混合序列.设且 1/p+1/q=1.则其中 (1/(αp))∧(1/(βq))表示1/(αp)和1/(βq)中最小者.

引理2[4]设 {Xn,n≥1}为 (α,β)混合序列满足如果EXn＜∞ 且则存在仅依赖于α,β和λ(·)的常数C，使得对任意n≥1和a≥0，

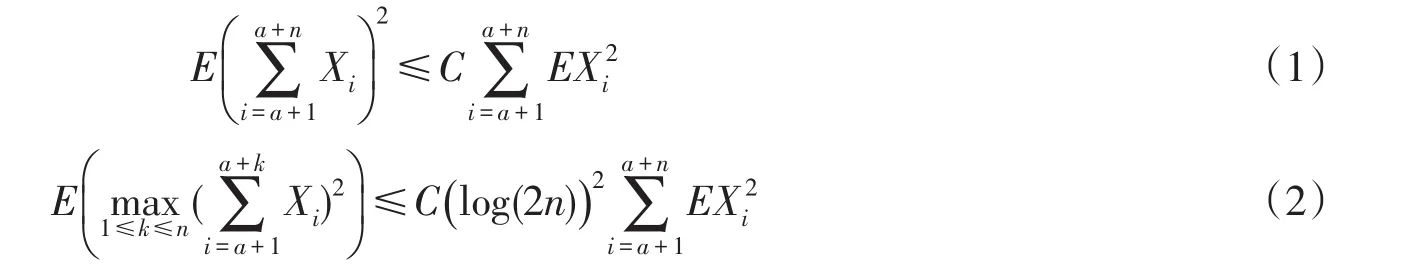
特别地

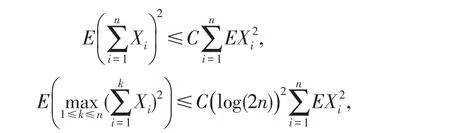
引理3[6]对任意的实数列{Xn,n≥1}，及对任意的n≥m≥1，有

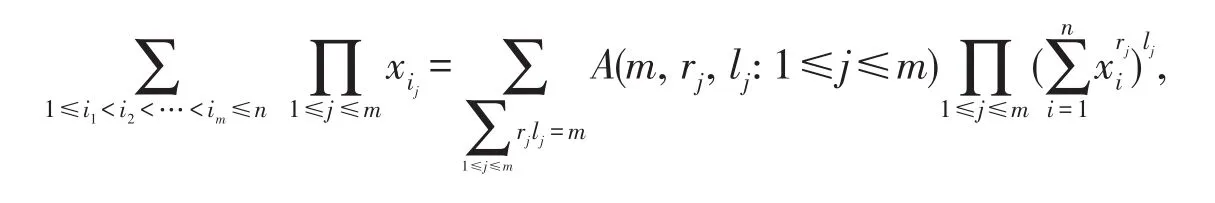
2 主要结果及其证明

定理1设{Xn,n≥1}为(α,β)混合序列，满足假设

定理1的证明 不失一般性，假设EXn=0,n≥1.设m＜n为正整数，由（1）式和（3）式，有

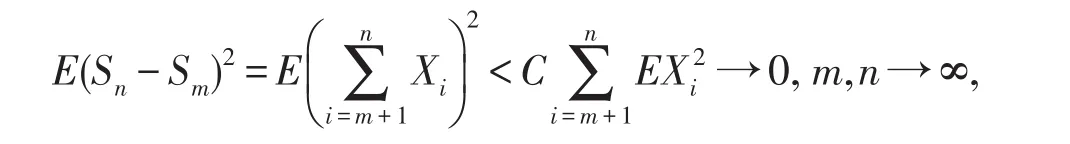
即{Sn,n≥1}是L2中Cauchy列.则存在一个随机变量S∈L2，使得当n→∞时，E(Sn-S)2→∞.结合（1）式和（3）式.可得对任意ε＞0，

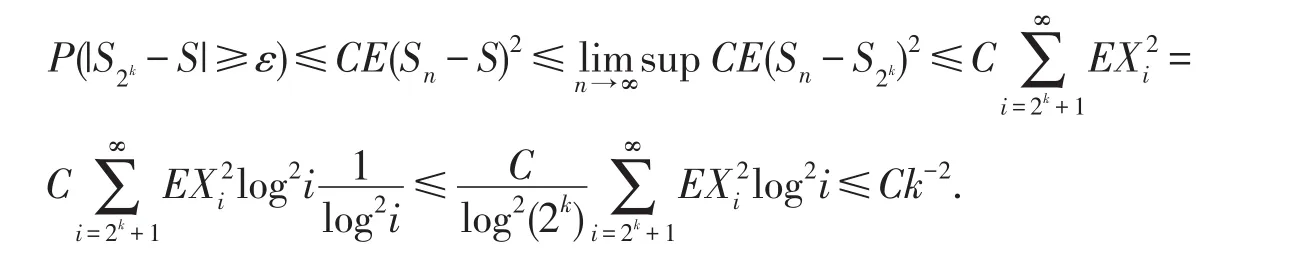
事实上，对任意ε＞0，由Markov不等式，（2～3）式，

再由Borel-Cantelli引理，可得（4）式成立.

定理2（推广的三级数定理） 设是(α,β)混合序列，满足对某a＞0 记如果

定理2的证明由（7）式，再由定理1有又由（6）式可知由（5）式由Borel-Cantelli引理得到所有除去概率为0的集外，{Xn,n≥1}和同时收敛或发散，从而收敛.

定理3设 {Xn,n≥1}是 (α,β)混合序列，满足是定义在R上的偶函数序列，在区间(x,∞)上取正值，且对任意的n≥1，存在λ＞0，使得下述条件之一成立：

1）gn(x)在(0,∞)内单调不减，且当0＜x＜1时，gn(x)≥λθ(0＜θ≤1);

同时，对于正常数序列{an,n≥1}，满足an↑∞，以及当p∈[1,2)时，若有

则

进一步我们有，对任意的m≥1,

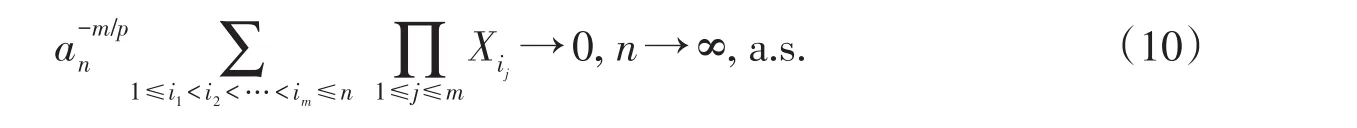
定理3的证明先证（9）式，令则

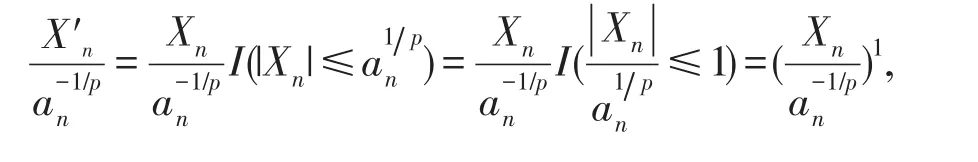
在条件1）下，gn(x)在(0,∞)内不减，所以即1则

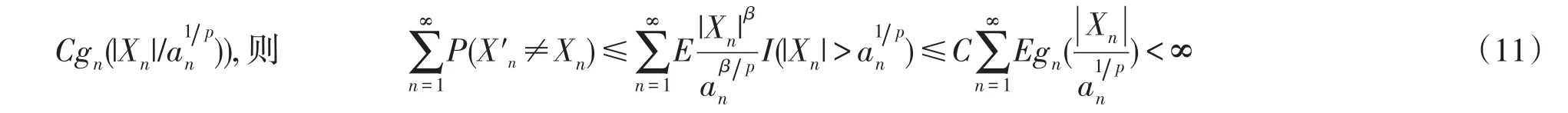
由Borel-Cantelli引理得到随机变量序列{Xn,n≥1}和{X′n,n≥1}是尾列等价的，于是要证（9）式，只需证明

在上述两个条件下，下面的证明是类似的，因此我们仅在条件2）下给出证明过程.

其次，又因为

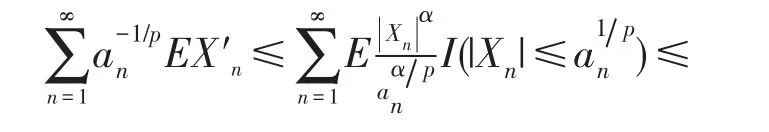
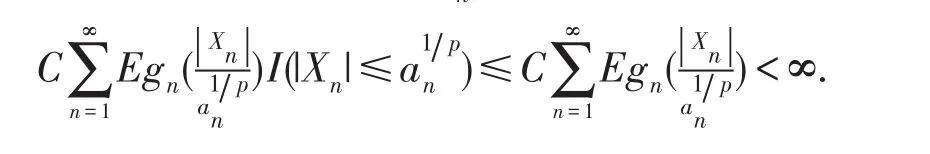
接下来，对给定的m≥1,由引理3可知，要证（10）式，只需证明，对任意的1≤r≤m，都有

由Cr不等式得

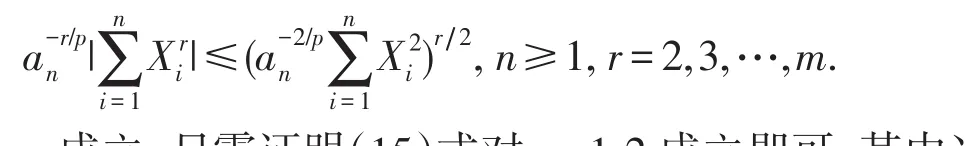
从而要证（15）式对r=1,2,…,m成立，只需证明（15）式对r=1,2成立即可，其中当r=1时，上述已证，当r=2时，由Borel-Cantelli引理及（11）式，只要证成立，于是由Kronecker引理可知（16）式成立.综上所述，定理3即证.

注意1 定理3中的条件（1）减弱为如下条件：

1）′gn(x)在(0,∞)不减，当 0＜x≤1时在这种情况下，条件（8）式加强为

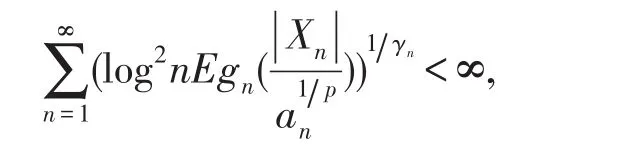
则定理3的结论仍然成立.

注意2 定理3中的条件（2）减弱为如下条件：

事实上，由（14）式的证明可以得到

在这种情况下，加上条件EXn=0,n≥1，其他条件不变，则定理3的结论仍然成立.

推论 1设 {Xn,n≥1}是 (α,β)混合序列，满足是正常数序列，满足是定义在R上的偶函数序列，在区间(0,∞)上取正值，且对任意的n≥1，使得下述条件之一成立：

3）fn,x/fn在 (0,∞)内不减；

4）fn/x,x2/fn在(0,∞)内不减，且EXn=0,n≥1.

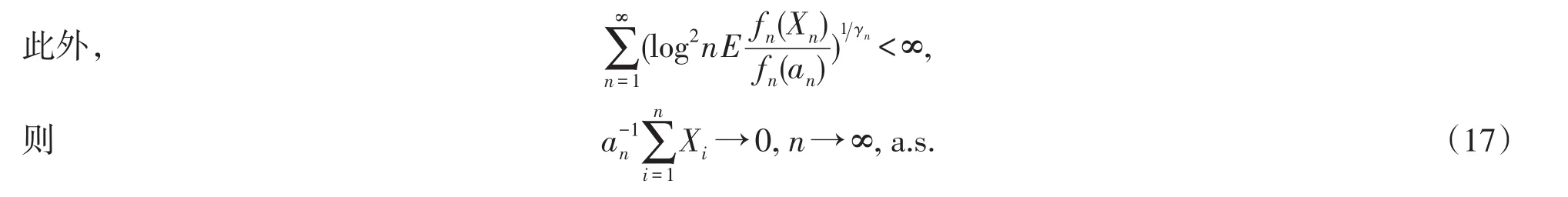
进一步我们有，对任意的m≥1,

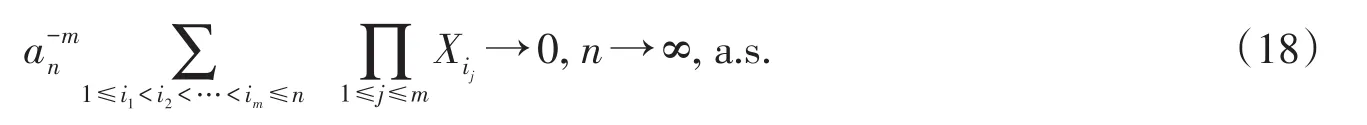
推论1的证明取gn(y)=fn(xy)/fn(x),对任意的x∈(0,∞),y∈R,则有gn(Xn/an)=fn(Xn)/fn(an),且gn(y)为在(0,∞)内取正值的偶函数.

同时，在条件3）下，函数gn(y)满足定理3的条件1），在条件4）下，函数gn(y)满足由注意2的条件2)′，而且

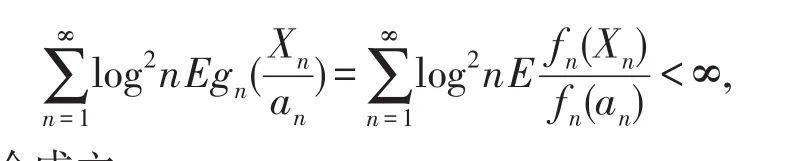
于是由注意2的结论知，推论1结论成立.

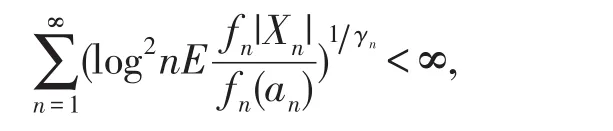
则（17）式成立，同时由定理3的结论，也可推出（18）式.

推论2的证明取gn(y)=fn(xy)/fn(x),对任意的x∈(0,∞),y∈R,则有gn(Xn/an)=fn(Xn)/fn(an),且gn(y)为在(0,∞)内取正值的偶函数.因为fn(X)在(0,∞)内不减，故有gn(y)在(0,∞)内不减.当0＜|Xn|≤an时，

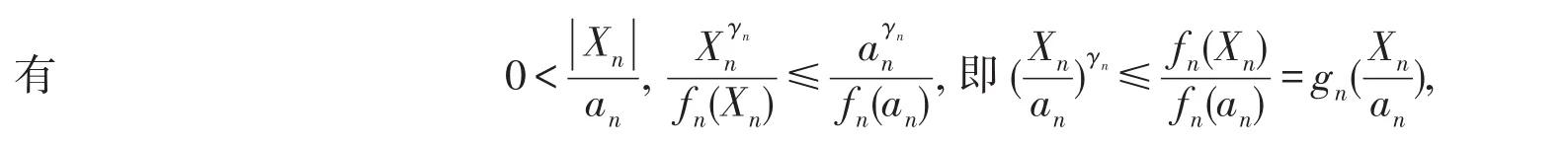
推论2设 {Xn,n≥1}是 (α,β)混合序列，满足是正常数序列，满足偶函数fn:R+→R+，满足fn(x)及xγn/fn(x)在(0,∞)内不减，其中γn≥2(n∈N)，若有

因此，当0＜y≤1时，有gn(y)≥yγn(γn＞2),又由fn(X)在(0,∞)内不减，gn(x)在(0,∞)内不减.由

从而满足注意1的条件1）′，再由定理3的结论知（17）式、（18）式成立.

在推论1中，取fn(x)=|x|r,r∈(0,2]，则有如下推论成立.

推论3设 {Xn,n≥1}是 (α,β)混合序列，满足是正常数序列，满足若有且当r∈(1,2]时，EXn=0,n＞1，则（17）式、（18）式成立.

推论3的证明显然fn(x)=|x|r为在区间(0,∞)内取正值偶函数.

当r∈(0,2]时，在区间(0,∞)内有下面式子成立：

fn(x)/x=|x|r/x=xr-1，当x增大时，xr-1不减，即fn(x)/x在(0,∞)内不减.

x2/fn(x)=x2/|x|r=x2-r，当x增大时，x2-r不减，即x2/fn(x)在(0,∞)内不减.因为所以

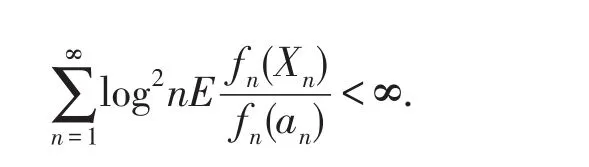
又因为当r∈(1,2]时，EXn=0,n＞1，从而fn(x)满足推论1的条件4）.因此推论3的结论成立.

［1]Bradley RC.The central limitquestion underabsolute regularity［J].Ann Probab，1985（4）：1314-1325.

［2]Shao QM.Almost sure invariance principles formixing sequences of random variables［J].Stochastic Processes and Their Applications，1993（2）：1-309.

［3]陆传荣，林正炎.混合相依变量的极限理论［M].北京：科学出版社，1997.

［4]沈燕，张永军，王学军，等.(α,β)混合序列的强极限定理［J].中国科学技术大学学报，2011（9）：778-784.

［5]Hu SH，Wang X J.Large deviations for dome dependetsequences［J].Acta Mathematica Scientia，2008（B）：295-300.

［6]王岳宝，严继高，成凤等.关于不同分布的两两NQD序列的Jamison型加权乘积和的强稳定性［J].数学年刊，2001，A（6），701-706.

［7]吴群英.混合序列的概率极限理论［M].北京：科学出版社，2006.

［8]万成高，陈芬.一类相依随机变量序列乘积和的强大数定律［J].数学研究，2008，（2），168-174.