NA列部分和乘积的极限定理
2015-10-19徐锋吴群英
徐锋,吴群英
(桂林理工大学理学院,广西 桂林 541004)
0 引言
定义1[1]称随机变量X1,…,Xn为NA(negatively associated)的,如果对于{1,2,…,n}的任何两个不相交的非空子集T1与T2,都有

其中f和g是任意两个使得协方差存在的且对每个变量均非降(或对每个变量均非升)的函数;称随机变量序列{Xn,n≥1}是NA序列,如果对任何自然数n≥2,变量X1,X2,…,Xn都是NA的.
NA随机变量是一包含独立随机变量在内的广泛的随机变量类,并且它在可靠性理论、渗透理论及多元统计分析理论等均有广泛的应用,因此对其的研究具有重要的意义.1983年,统计学者Joag-Dev和Proschan正式引入了NA随机变量的概念后,迄今对NA随机变量概率性质及其应用的研究已经获得了很多深入的结果.
为了便于讨论,先叙述与本文中相关的已有结果.众所周知,对于独立同分布正的平方可积的随机变量的乘积是渐近对数正态的.对{Xn,n≥1}服从指数分布独立同分布的随机变量序列,且EX1=1,Aronold和 Villaseñr[2]首先得到了


Rempała和Wesołowski[3]改进了这一结果,移除了文献[2]中{Xn,n≥1}服从指数分布的条件,得到了对i.i.d.正的随机变量序列部分和乘积的中心极限定理,即
定理A[3]设{Xn,n≥1}是i.i.d.正的平方可积的随机变量序列,EX1=μ,varX1=σ2>0,变异系数γ=σ/μ,则

其中,N表示标准正态随机变量.
Gonchigdanzan和Rempała[4]讨论了上述形式的几乎处处中心极限定理,得到了如下的结果.
定理B[4]设{Xn,n≥1}是i.i.d.正的平方可积的随机变量序列,EX1=μ,varX1=σ2>0,变异系数γ=σ/μ,则

其中F(·)是随机变量的分布函数,N表示标准正态随机变量.
Yu[5]针对部分和乘积的极限定理,给出了另一种形式的中心极限定理和几乎处处中心极限定理.
定理C[5]设{Xn,n≥1}是i.i.d.正的平方可积的随机变量序列EX1=μ,varX1=σ2>0,变异系数γ=σ/μ,令
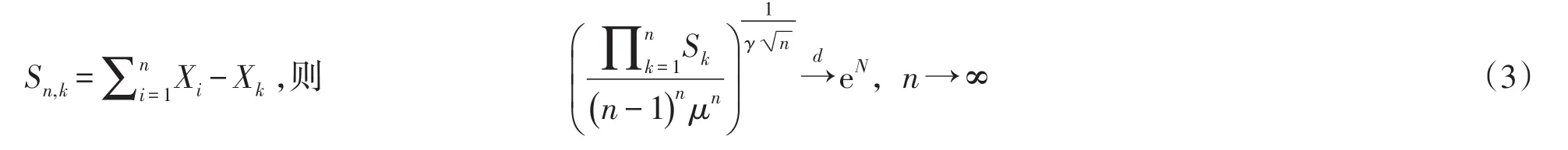
对∀x∈R,有)

其中F(·)是随机变量eN的分布函数,N表示标准正态随机变量.
叶大相和吴群英[6]在Yu[5]的基础上对部分和乘积的几乎处处中心极限定理中的权重dn做了进一步的推广,给出了如下的定理.
定理D[6]设{Xn,n≥1}是i.i.d.正的随机变量列EX1=μ,varX1=σ2>0,变异系数则对∀x∈R,有
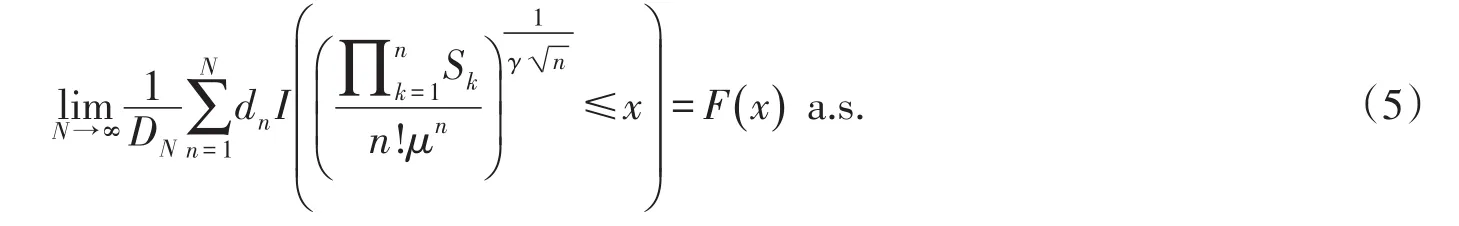
其中F(·)是随机变量eN的分布函数,N表示标准正态随机变量.
针对定理C和定理D,将其推广到了NA列,并将(5)式的权重dn作了推广.假设{Xn,n≥1}是平稳的NA列,我们知道是存在的,且进一步,若那么其中参阅文献[7-8])以下记表示存在一个常数c使得an≤cbn.符号“→d”表示依分布收敛表示依概率收敛.c表示与n无关的正常数,在不同地方可表示不同的值.并假设0<cn→∞,且
1 主要定理
定理1 设{Xn,n≥1}是平稳正的NA随机变量序列,EX1=μ,varX1=σ2>0,记Yi=(Xi-μ),i≥1,满足

则

其中N表示标准正态随机变量.
定理2设{Xn,n≥1}是平稳正的NA随机变量序列,EX1=μ,varX1=σ2>0,记Yi=(Xi-μ),i≥1,满足
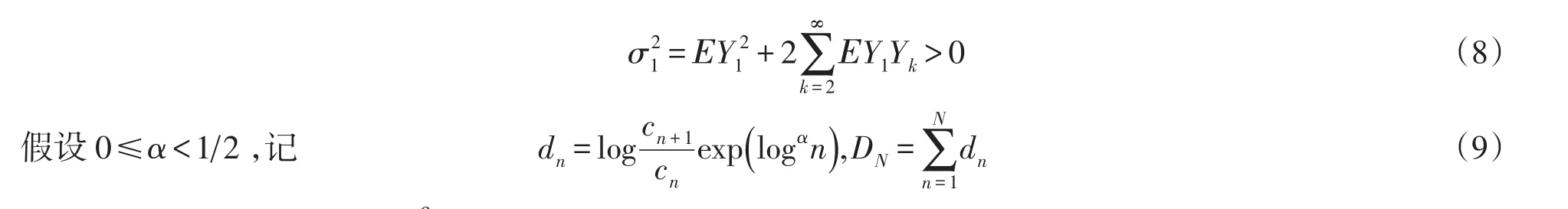
且存在常数β>0,使得则对∀x∈R,有
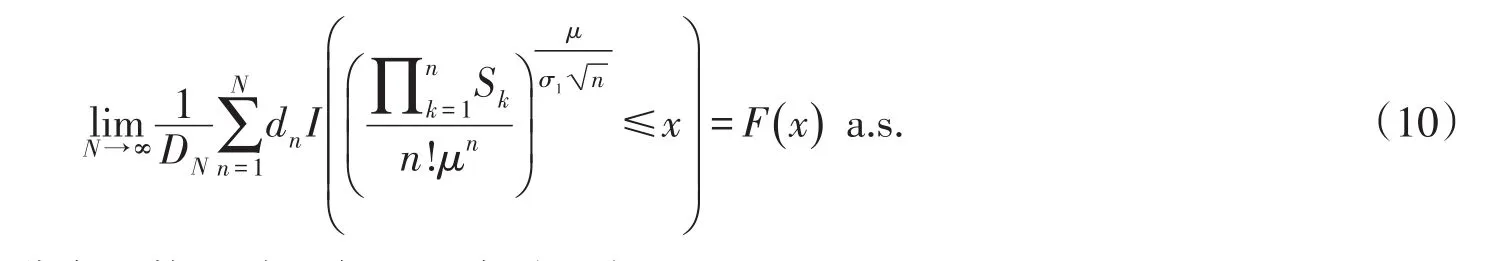
其中F(·)是随机变量eN的分布函数,N表示标准正态随机变量.
注1 因为i.i.d.随机变量序列是NA序列的特殊情况,故对NA列的成立i.i.d.的随机变量序列也成立.当{Xn,n≥1}为i.i.d.序列,(6)式的因此(7)式成立,(3)式也成立.
注2[9]假如用满足的权重序列去替代{ }dn,n≥1 ,(10)式仍然成立.
注3 如果取cn=n,则(9)式中当{Xn,n≥1}为i.i.d.序列,(8)式的var()X1,因此定理2不仅将定理D从独立情形推广到了NA列,也将权重dn进行了推广.
2 定理的证明
先介绍证明中需要的两个引理.
引理1[9]设{Yi,i≥1}是平稳的NA列,满足假设存在常数β>0,使得则对∀x∈R,有
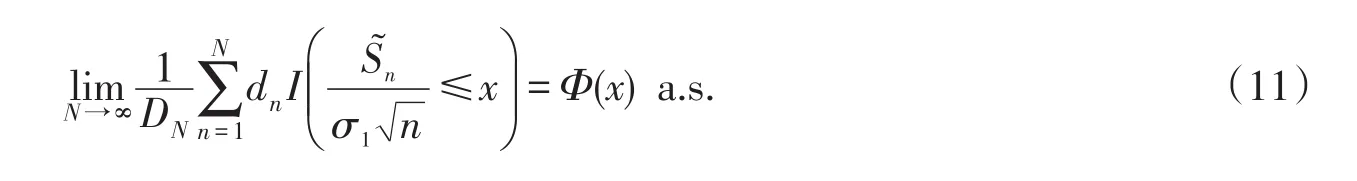
引理2[10]设{Xi,i≥1}为同分布NA序列,记,则对0<p<2,使得

成立的充要条件是:E|X1|p<∞;且当0<p<1时,b可为任何实数;当1≤p<2时,b=EX1.
定理1的证明(7)式等价于


从而得到

其中θk∈(0,1),k=1,2,…,n.
首先我们估计A1,记显然,{Yi,i≥1}是NA的.且则

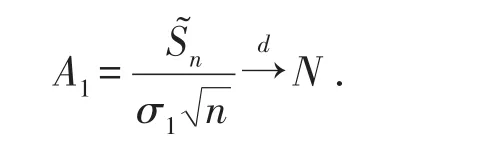
现在估计A2.对某一固定的k,1≤k≤n,及∀ε>0有

因此,根据a.s.收敛的判别准则(参阅文[11]中定理1.5.2)可知

关于k一致成立.
再由引理2可知,

关于k一致成立.从而有


另一方面,因为

以及当|x|<1/2,有x2/(1+θx)2≤4x2.故对任意的θ∈(0,1),有

这就完成了定理1的证明.
定理2的证明因为(10)式等价于
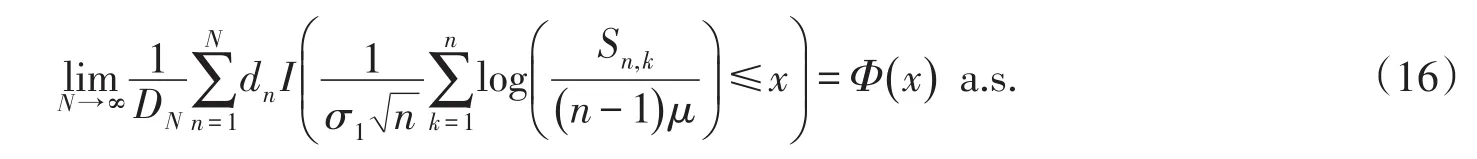


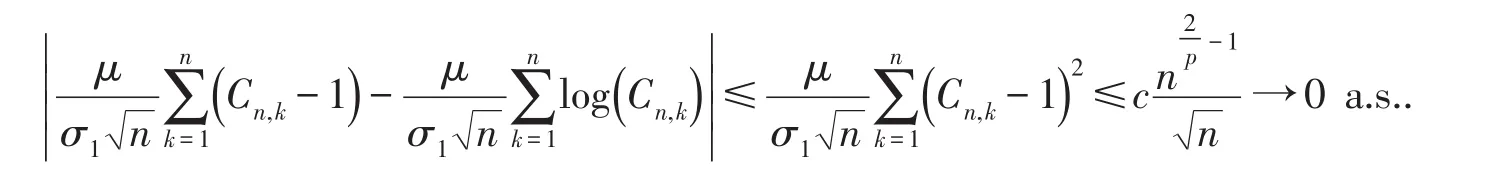
所以当n→∞,有

利用(17~18)式立即得(16)式.这就完成了定理2的证明.
[1]Joag-Dev K,Proschan F.Negativeassociation of random variableswith applications[J].Ann Statist,1983,11:286-295.
[2]Arnold BC,Villaseñr JA.Theasymptotic distribution ofsumsof records[J].Extremes,1998,1(3):351-363.
[3]RempałaGA,Wesołowski J.Asymptotics for productsofsums and U-statistics[J].Electron Comm Probab,2002(7):47-54.
[4]Gonchigdanzan K,Rempała G A.A note on the almost sure limit theorem for the product of partial sums[J].Applied Mathematics Letters,2006,19:191-196.
[5]Yu M.Central limit theorem and almost sure central limit theorem for the product of some partialsums[J].Proc Indian Acad Sci(Math Sci),2008,118(2):289-294.
[6]叶大相,吴群英.部分和乘积的几乎处处中心极限定理[J].桂林理工大学学报,2011,31(3):471-472.
[7]Wu Q Y,Jiang Y Y.Almost sure central limit theorem for self-normalized partial sums of negatively associated random variables[J].Discrete Dynamics in Nature and Society,2014(1):1-9.
[8]Newman C M.Asymptotic independence and limit theorems for positively and negatively dependent variables[J].Statist Probab Lett,1984:127-140.
[9]苏淳,王岳宝.同分布NA序列的强收敛性[J].应用概率统计,1998,14(2):131-140.
[10]Wu Q Y.An almost sure central limit theorem for theweight function sequences of NA random variables[J].Proc Indian Acad Sci(Math Sci),2011,121(3):369-377.
[11]吴群英.混合序列的概率极限理论[M].北京:科学出版社,2006:17.
