φ~混合序列部分和的完全收敛性质

王瑶，黄海午

（1.太原工业学院理学系，山西 太原 030008；2.衡阳师范学院数学与计算科学系，湖南 衡阳 421002）

1 引理

假设(Ω,F,P)表示一个概率空间，{Xn,n≥1}是定义在该概率空间上的随机变量序列，FS=σ(Xi;i∈S⊂ℕ) 表示σ-域，有限子集S,T⊂ℕ为非空的.在F中给定两个σ-域ξ和ℜ，令：

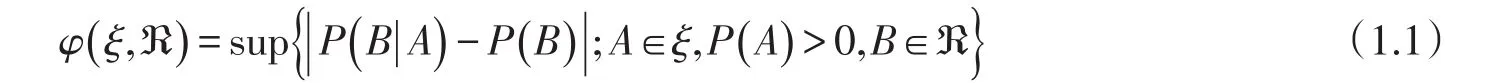
定义设随机变量序列{Xn,n≥1}，若存在自然数k∈ℕ使得则称序列{Xn,n≥1}为混合序列.

注意到，如果{Xn,n≥1}为独立随机变量序列时，则混合与通常的混合有一定的类似，但并不相同，且互不包含.事实上，在通常的混合系数(k)中，（1.2）式中的S和T分别是[1 ,k]和[k+n,∞ )中的子集，而混合只要求存在某个k≥1，使得φ~(k) ＜1，从而比φ~混合的要求k→∞要弱得多.因此，混合序列是一类较广泛的相依序列，有相当多的文献对其极限收敛性质进行了研究，如：黄海午等[1]讨论了混合序列加权和的完全收敛性；LIU Tingting等[2]研究了~混合序列加权和的强大数定律；葛梅梅等[3]建立了混合序列加权和的强收敛性质的充分条件，等等.笔者讨论混合序列部分和的完全收敛性，所获结果推广和改进了王学军等人[4]关于φ~混合序列部分和强大数定律的结果，并且所用证明方法与文献［4]中的方法完全不同.

引理1设{Xn,n≥1}是一列φ~混合序列，若，则存在一个常数仅依赖于q，k和有

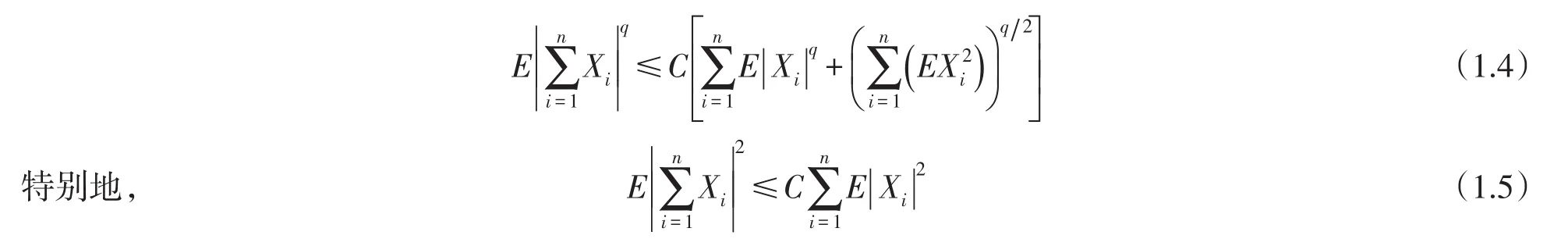
上述引理类似于吴群英[5]中的引理5.1.1，此处证明省略.

引理2设{un,n≥1}和{vn,n≥1} 是非负数列，且un≤vn，∀n≥1.则无穷级数

本文中约定：C总表示正整数，在不同的地方可以表示不同的值，Ⅰ(A)表示事件A的示性函数.

2 主要结果及证明

定理1设{Xn,n≥1}为一列φ~混合序列，{an,n≥1}为正常数列.设{gn(t),n≥1}为实数ℝ 上的偶函数序列，在区间t＞0中取正值、不减；对于每个n≥1，序列{gn(t),n≥1}满足下列条件之一：

（i）在区间t＞0中，存在p∈(0 ,1] ，使得单调不减；

（ii）在区间t＞0中，存在p∈(1 ,2 ]，使得和单调不增，且EX=0.若n

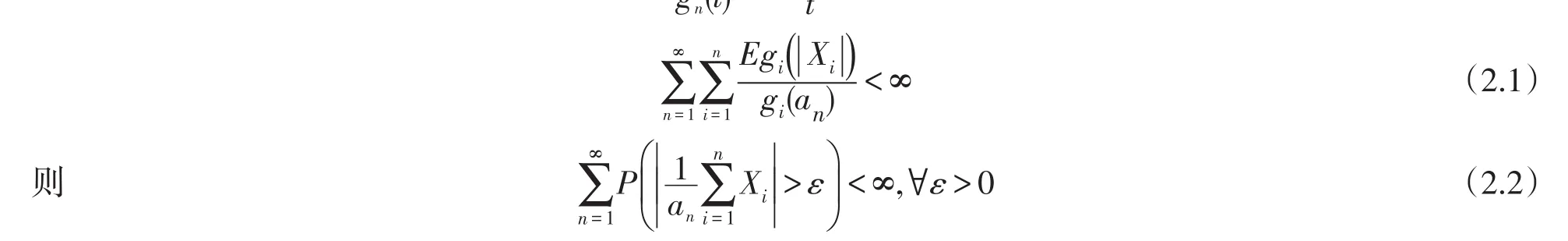
定理1的证明对所有的n≥1，定义从而对∀ε＞0有

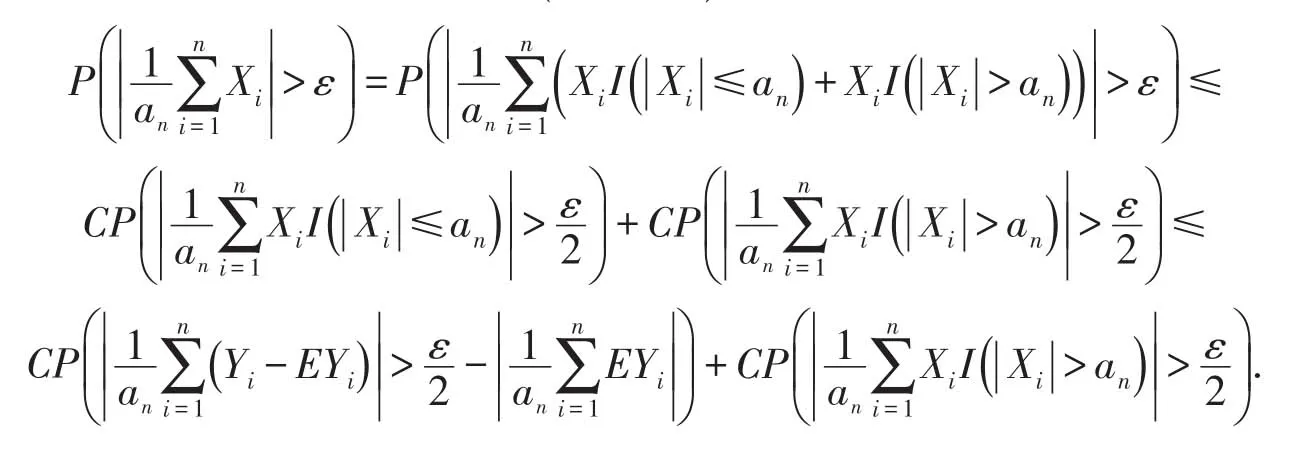
即要证明定理1成立，只需证明：

1）假设序列{gn(t),n≥1} 满足条件（i），则在区间|Xn|≤an中，

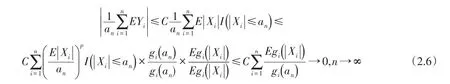
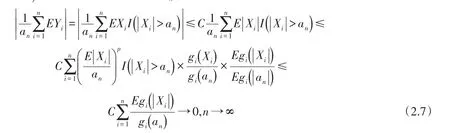
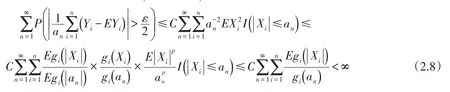
最后，（2.3）式的证明类似于（2.5）式证明.此处仅证明序列满足条件（ii）时，可得

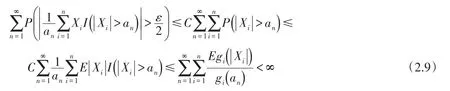
定理1证明完成.

推论1在定理1的条件下，有

推论2在定理1的条件下，若

则（2.2）式和（2.10）式成立.在定理1的类似条件下，沈建伟[6]研究了两两NQD序列的极限定理，得到了两两NQD序列的强大数定律结果.笔者利用定理1条件，研究并得到了φ~混合序列部分和的完全收敛性定理，所获结论更强.

定理2设为一列φ~混合序列为正常数列.设为实数ℝ上的偶函数序列，在区间t＞0中取正值、不减；对于每个n≥1，序列{gn(t),n≥1}满足：假设存在某个常数p∈[2,∞)使得单调不减.若

则对于∀ε＞0，（2.2）式和（2.10）式成立.

定理2的证明使用与定理1相同的记号，证明过程类似于定理1.首先，证明（2.5）式成立.实际上，由Holder不等式和（2.12）式可得：

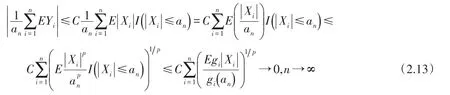
从而（2.5）式成立.

其次，证明（2.4）式成立.由于p≥2，所以结合（2.12）式和引理2可得：

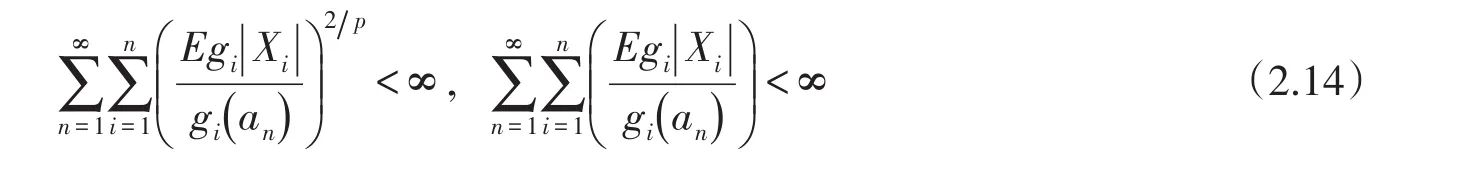
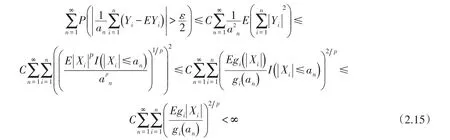
上述第二个不等式是利用：当r＞0时关于r单调递增的.

最后，证明（2.3）式成立.当||Xi＞an＞0时，

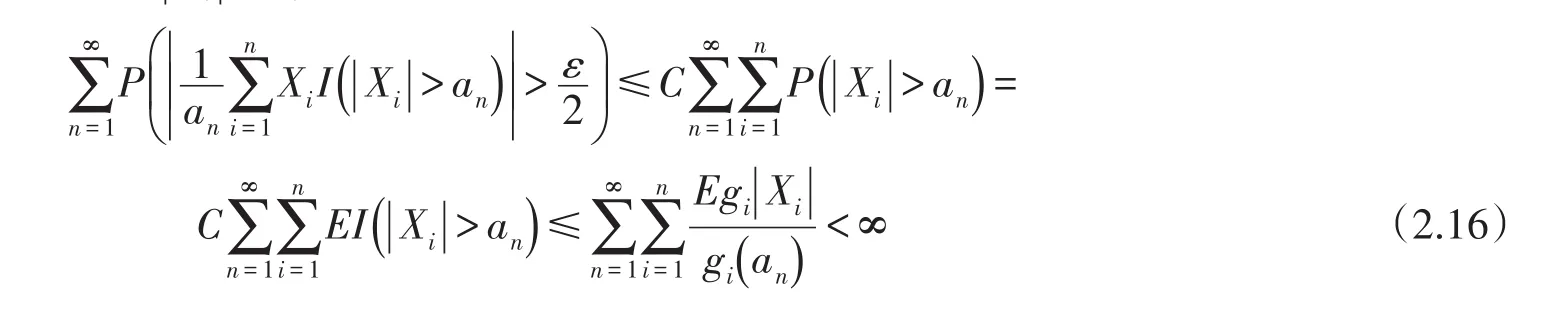
从而定理2证明完成.

［1]黄海午，王定成，彭江艳.φ~混合随机变量加权和的完全收敛性［J].数学杂志，2014，34（1）:31-36.

［2]LIU Tingting，CHEN Zhiyong，WANGXuejun，etal.Strong lawsof largenumbers forweighted sumsofφ~-mixing sequence［J].Chin Quart JofMath，2013，28（4）:578-584.

［3]葛梅梅，邓新，陈志勇，等.φ~混合序列加权和的强收敛性［J].高校应用数学学报，2013，28（4）:424-430.

［4]王学军，胡舒合，沈燕.φ~混合序列部分和的收敛性质［J].工程数学学报，2009，26（1）:183-186.

［5]吴群英.混合序列的概率极限理论［M].北京：科学出版社，2006.

［6]沈建伟.两两NQD列的一个强大数定律［J].浙江科技学院学报，2012，24（4）:265-268.