一个与小函数有关的微分多项式不等式估计

徐俊峰

（1.湖南大学数学与计量经济学院，长沙湖南410082；2.五邑大学数学与计算科学学院，江门广东529020）

一个与小函数有关的微分多项式不等式估计

徐俊峰1，2

（1.湖南大学数学与计量经济学院，长沙湖南410082；2.五邑大学数学与计算科学学院，江门广东529020）

利用精简计数函数证明了关于φf2f（k）-1的定量估计不等式，这里f是一个超越亚纯函数，φ是关于f的小函数.此不等式推广了以往的结果.

亚纯函数；微分多项式；值分布；小函数

1　引言与定理

设f（z）是亚纯函数，如果a（z）是一个非恒为零亚纯函数满足T（r，a）=S（r，f），这里S（r，f）=o（T（r，f））（r→∞），除了关于r的一个可能存在的有限例外集，称a（z）是f（z）的小函数.假设读者熟悉值分布的相关理论（参考文献［1-6］）.

定义1.1设k是一个正整数，a是任意一个复数.Nk）（r，1/（f-a））表示关于f-a的零点重数小于等于k的计数函数，N（k（r，1/（f-a））表示关于f-a的零点重数大于等于k的计数函数，Nk（r，1/（f-a））表示关于f-a的零点重数等于k的计数函数.另外，与分别表示上述函数相应的精简计数函数.

1982年，文献［7］证明了下述结果.

自然地，当n=2时上述定理对应的情况怎么样？最近，文献［8］得到了一个关于f2f（k）-1的结果.

定理1.2设f是一个超越亚纯函数及k是一个正整数，那么

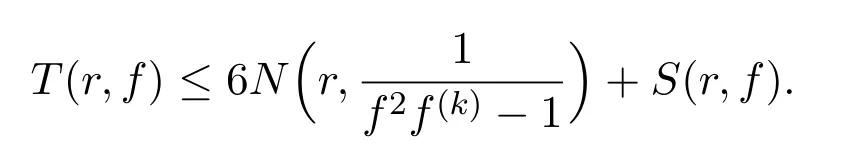
注1.1事实上，文献［9］证明了k=1的情况.文献［8］证明了k≥2的情况.文献［10］利用精简计数函数改进了定理1.2得到了如下结果.

定理1.3设f是一个超越亚纯函数，k是一个正整数.那么

当k=1或k≥3时，M=6；当k=2时，M=10.

对应于定理1.1，自然地考虑f2f（k）-a（z）的值分布情况，这里a（z）是f（z）的一个小函数.本文研究了这个问题得到了下述结果.

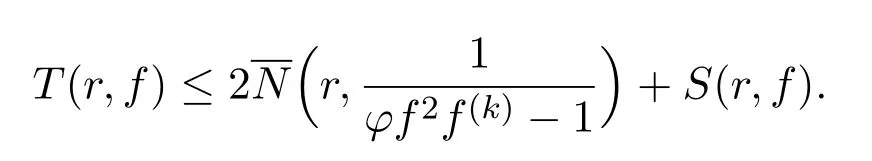
2　引理

为了证明主要的结果，引入下述引理.

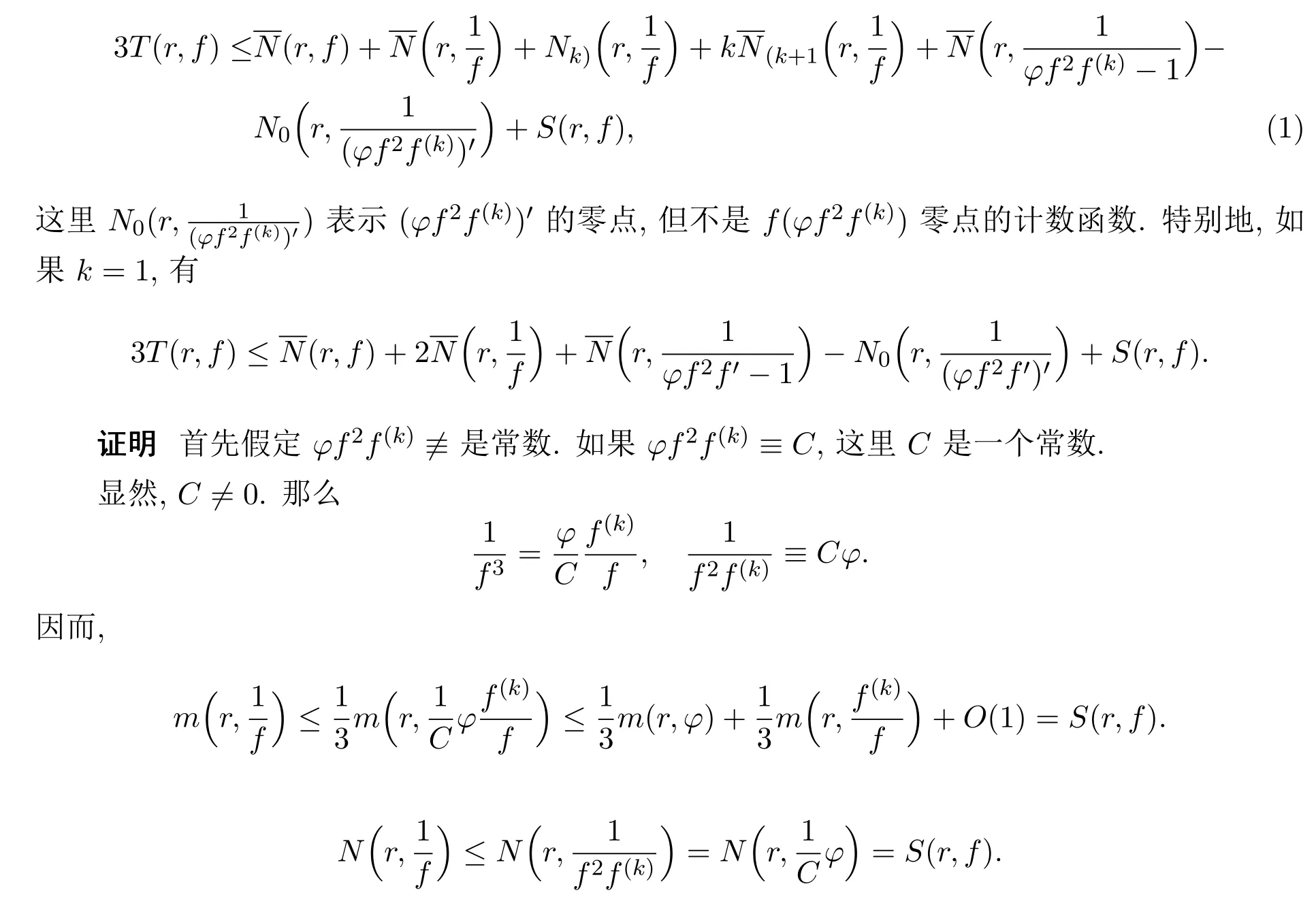
假设z0是f的重数为q的零点且是φ的重数为t的极点.

情况I假设t≤2q-1，如果q≤k，那么z0是（φf2f（k））′的重数至少为2q-1-t的零点；如果q≥k+1，那么z0是（φf2f（k））′的重数至少为3q-（k+1）-t的零点.

情况II假设t≥2q，z0至多是φ2的极点.因而有

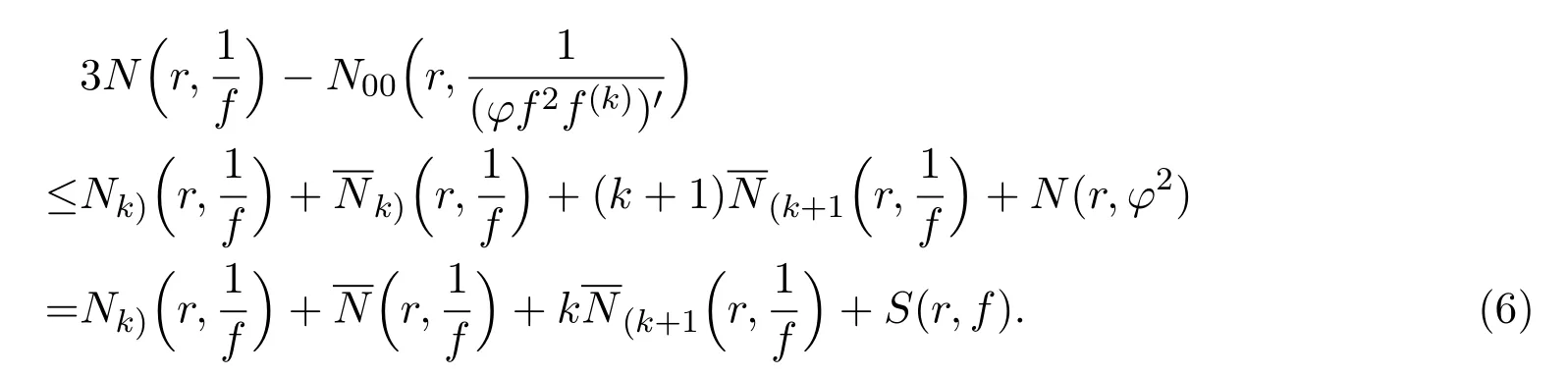
由（3）-（6）式，有

下面，首先构造一个辅助函数来去掉（1）中极点的限制.

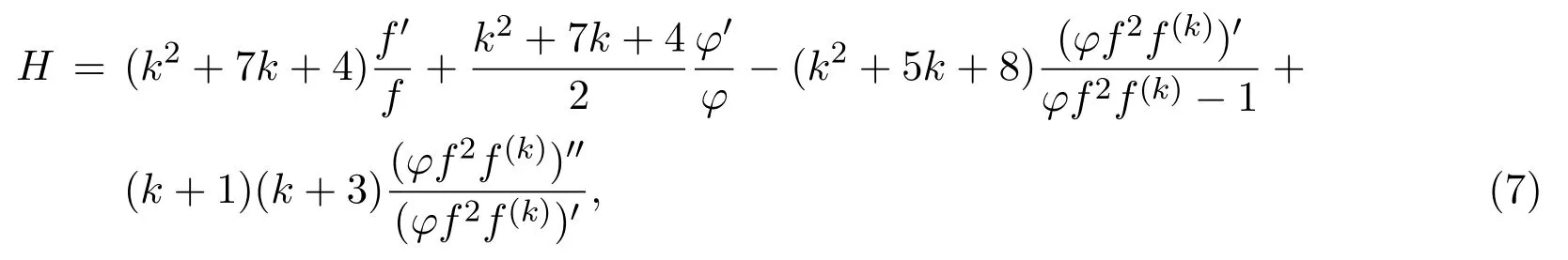
证明（I）如果H（z）≡0.通过对等式（7）两边的积分，有

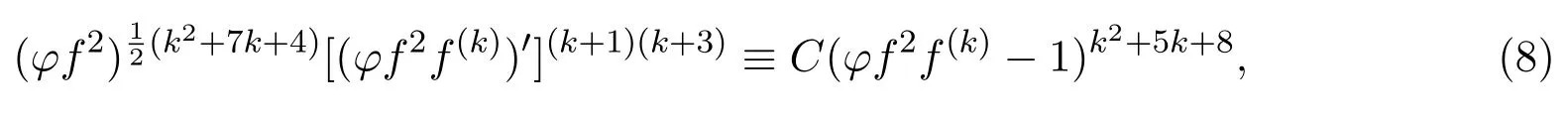
这里C是一个非零的复常数.

由（8）式知道f（z）的零点来自于φ（z）的极点.如果f（z）存在一个零点z1，设z1是f（z）的零点具有重数p（≥3），且为φ（z）的极点具有重数q（≥1）.如果p＞2q，那么z1是φf2的零点具有重数p-2q.因而C=0.这是一个矛盾，因而p≤2q，有

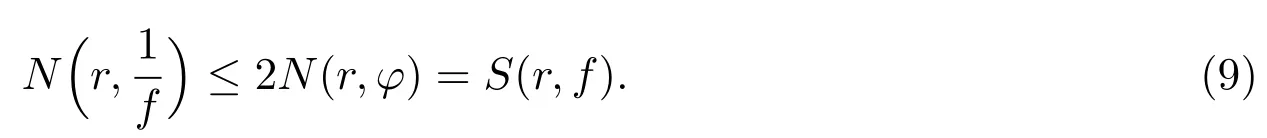
（8）式可以改写为

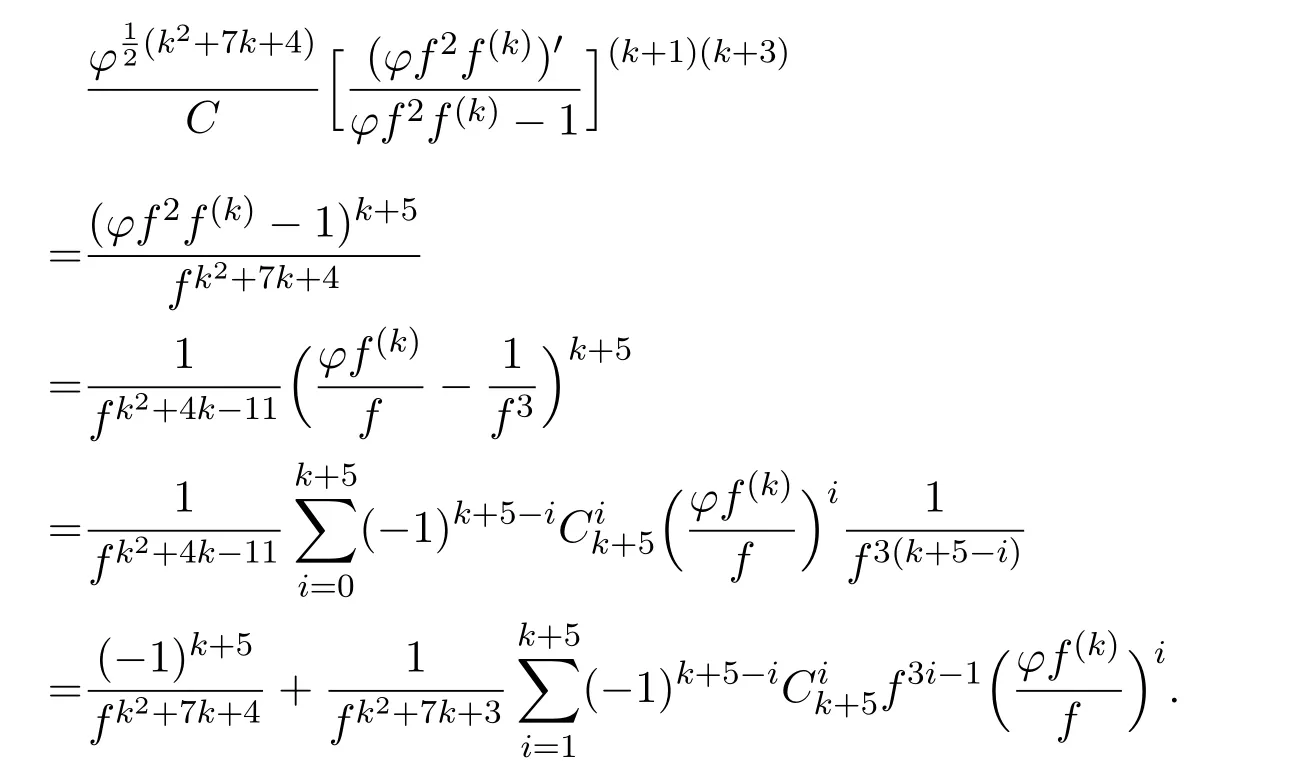
也就是说

设Er=｛θ||f（z）|≤1；z=reiθ，θ∈［0，2π］｝.如果|f（z）|≤1，有

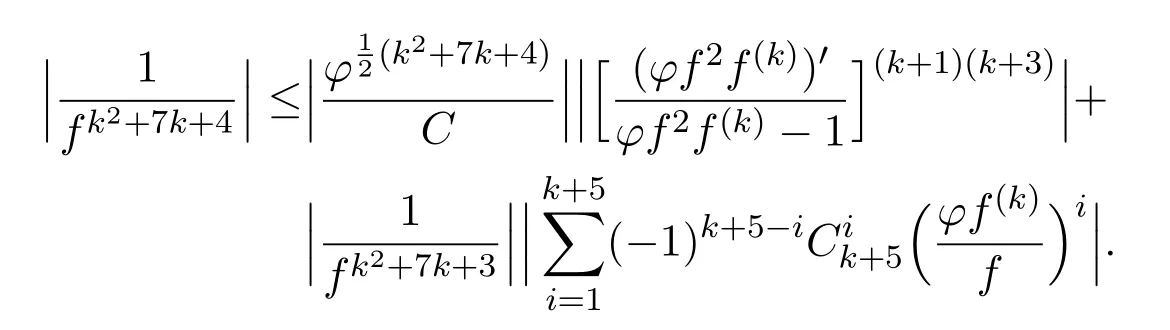
因而有

（II）设z2是f（z）的单极点而不是φ（z）的零点和极点，那么f（z）和φ（z）在z2的邻域有下列展开式：

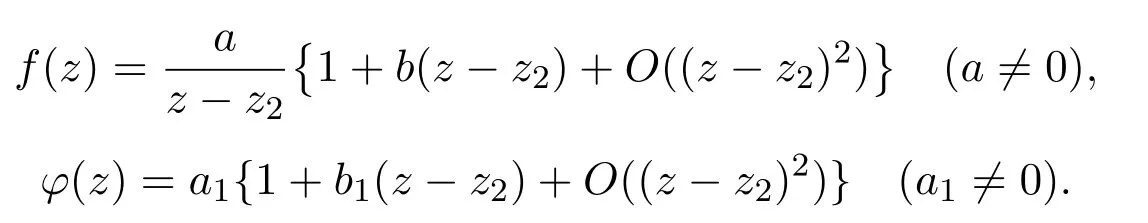
由此容易得到

将（10）式-（13）式代人（7）式，得到

因而z2是H（z）的零点.即f（z）的单极点若不是φ（z）的零点和极点必为H（z）的零点.

引理2.3设f是一个超越亚纯函数，且k是一个正整数.那么

引理2.4设f是一个超越亚纯函数，且k是一个正整数.那么

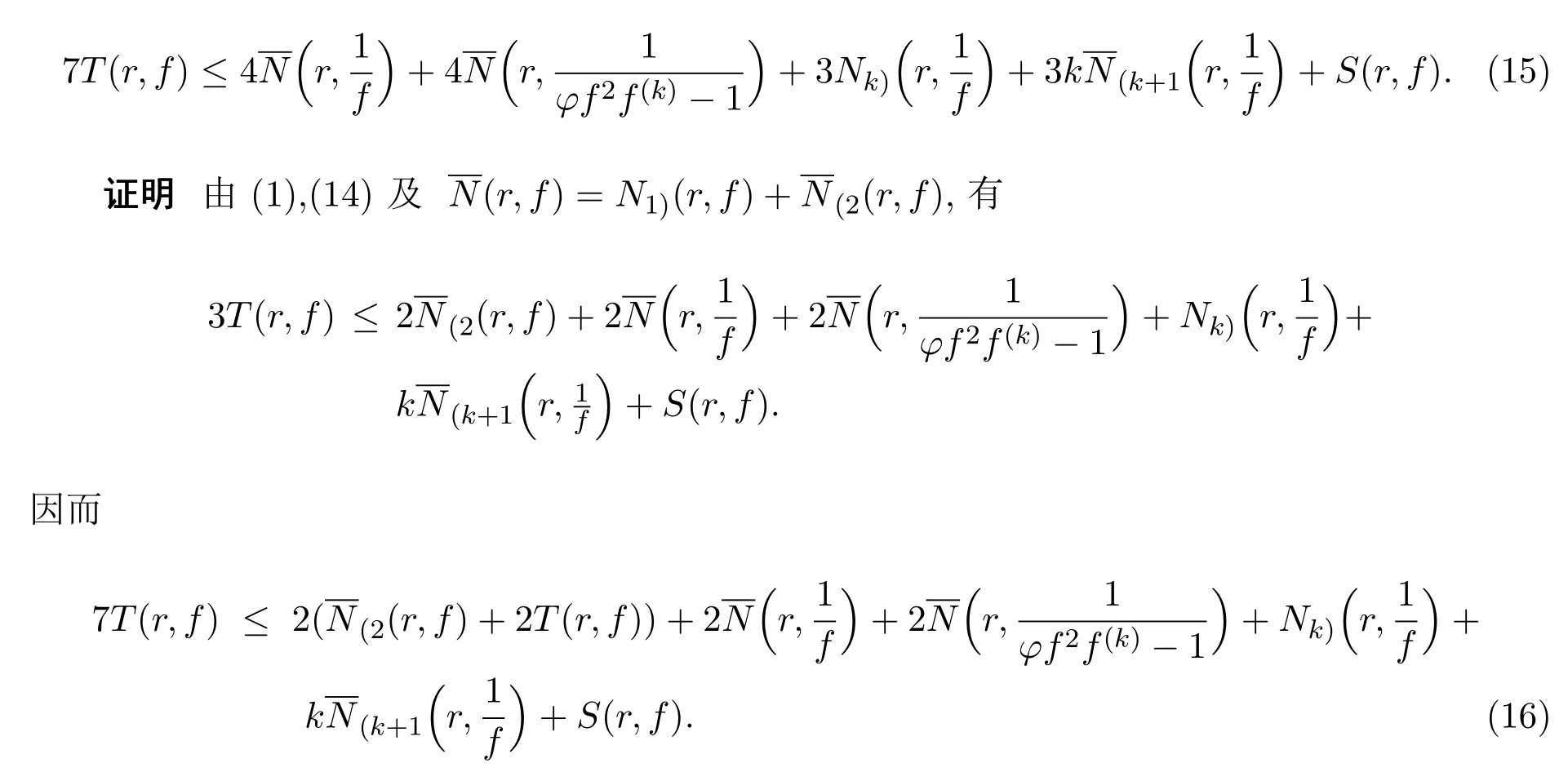
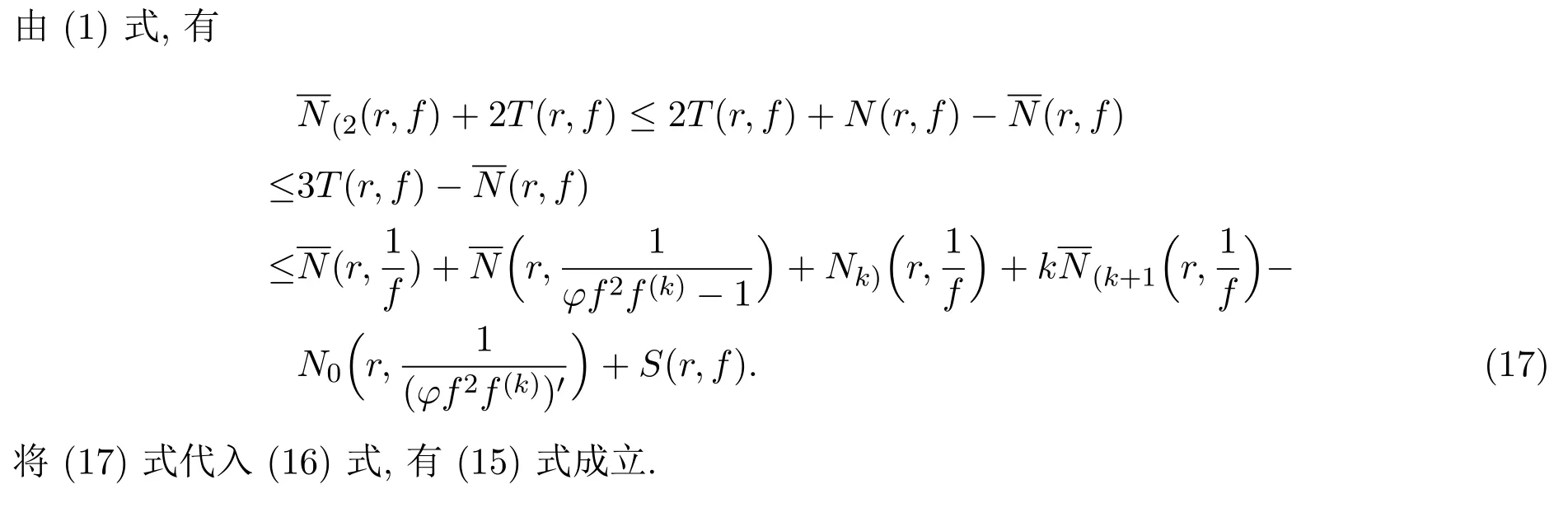
3　定理1.4的证明

分两种情况证明：

情形1k=1.

情形2k≥2.

因而有

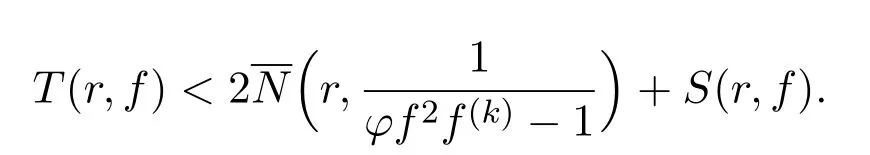
完成了定理1.4的证明.

［1］Hayman W.Meromorphic Functions［M］.Oxford：Clarendon Press，1964.

［2］Laine I.Nevanlinna Theory and Complex Differential Equations［M］.New York：Walter de Gruyter，1993.

［3］徐俊峰，仪洪勋.微分方程的解和小函数的关系［J］.数学学报，2010，53（2）：85-90.

［4］Yamanoi K.The second main theorem for small functions and related problems［J］.Acta Math.，2004，192：225-294.

［5］Yang L.Value Distribution Theory［M］.New York：Springer，1993.

［6］仪洪勋，杨重骏.亚纯函数唯一性理论［M］.北京：科学出版社，1995.

［7］Doeringer W.Exceptional values of differential polynomials［J］.Pacific J.Math.，1982，98（1）：55-62.

［8］Huang X J，Gu Y X.On the value distribution of f2f（k）［J］.J.Aust.Math.Soc.2005，78：17-26.

［9］张庆德.亚纯函数的一个增长性定理［J］.成都信息工程学院学报，1992，20：12-20.

［10］Xu J F，Yi H X，Zhang Z L.Some inequalities of differential polynomials II［J］.Mathematical Inequalities and Applications，2011，14（1）：93-100.

An inequality of differential polynomials related to small function

Xu Junfeng1，2
（1.Department of Mathematics，Hunan University，Changsha 410082，China；2.School of Mathematics and Computational Science，Wuyi University，Jiangmen529020，China）

In this paper，a quantitative estimate of the differential polynomials φf2f（k）-1 is obtained，where f is a transcendental meromorphic function，φ is a small function and k is a positive integer，by the reduced counting function when f has few simple zeros.This result improves the existed theorems.

meromorphic functions，differential polynomials，value distribution，small functions

O174.52

A

1008-5513（2015）05-0441-08

10.3969/j.issn.1008-5513.2015.05.001

2015-03-10.

国家自然科学基金（11126327）；广东省自然科学基金（9452902001003278）；广东省高校优秀青年教师培养对象项目（Yq2013159）.

徐俊峰（1979-），博士后，教授.研究方向：主要从事复分析研究.

2010 MSC:30D35