置换空间PXXn的范数k-粗性

秦璇，苏雅拉图

（内蒙古师范大学数学科学学院，内蒙古呼和浩特010022）

置换空间PXXn的范数k-粗性

秦璇，苏雅拉图

（内蒙古师范大学数学科学学院，内蒙古呼和浩特010022）

利用Banach空间理论的方法，主要研究了k-粗性和k-强粗性从Banach空间Xn到置换空间PXXn上的提升问题，证明了这两种k-粗性都可以在置换空间PXXn上得到提升.

置换空间；k-粗范数；k-强粗范数；k-点态粗范数

1　引言

Banach的凸性与光滑性研究是Banach空间几何学的主要研究对象之一.为了研究光滑性较差的Banach空间范数的性质，文献［1］提出并研究了粗范数这一概念，在此基础上，文献［2］中引进并讨论了强粗范数这一概念，强粗范数是比粗范数更强的概念，即具有强粗范数的Banach空间的光滑性要比具有粗范数的Banach空间的光滑性差.这两个概念在刻画光滑性较差的Banach空间特征时起到了重要作用，它们也成为了研究光滑性较差的Banach空间的有力工具.文献［3］中进一步研究了粗范数和强粗范数的特征刻画及性质，完善了光滑性较差的Banach空间的研究.为了研究光滑性更差的Banach空间范数的性质，文献［4-5］作为粗范数和强粗范数的相应推广引入了k-粗范数与k-强粗范数（k=1时，1-粗范数与1-强粗范数分别等价于粗范数与强粗范数），研究了k-粗范数与k-强粗范数，并把k-粗性和k-强粗性提升到了Banach序列空间lp（Xi）.文献［6］于1977年引入的置换空间是包含lp（Xi）在内的更广泛的一类Banach空间，于是本文考虑了k-粗性和k-强粗性在置换空间PXXn上的提升问题，并对此问题得到了肯定的回答.

本文中，X表示Banach空间，S（X）和S（X∗）分别表示X及X∗的单位球面，对x∈X，令∑（x）=｛f∈S（X∗）：f（x）=‖x‖｝，对x1，x2，···，xk+1∈S（X），令

2　定义及引理

定义2.1［4］Banach空间X的范数称为k-粗的，若存在ε＞0，使∀x∈S（X），f∈∑（x）和δ＞0，存在y1，···，yk∈S（X）及gi∈∑（yi），i=1，···，k，使得当‖yi-x‖＜δ时，有A（f，g1，g2，···，gk）≥ε.

定理2.1［4］Banach空间X的范数是k-粗的当且仅当对任意的x∈S（X），存在ε＞0和fn1，···，fnk+1∈S（X∗），使得当

定理2.2［5］Banach空间X的范数称为k-强粗的，若存在ε＞0，使∀x∈S（X），f，g1，g2，···，gk∈∑（x），有

定理2.3［4］设X是Banach空间，x∈S（X）称为范数的k-粗糙点，若存在ε＞0，使∀f∈∑（x）和δ＞0，存在y1，···，yk∈S（X）及gi∈∑（yi），i=1，···，k，满足

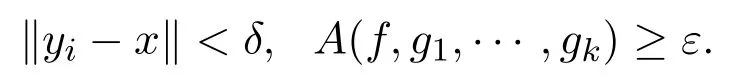
定义2.1［4］Banach空间X的范数称为k-点态粗的，若S（X）的点是范数的k-粗糙点.

定义2.2［7］设X是有超正交基（xn）的空间，（Xn）是一列Banach空间，令

引理2.1［7］如果X有超正交基（xn），且（xn）的共轭序列是（X∗）的基，则（x∗n）是（X∗）的超正交基且（PXXn）∗等距同构于PX∗X∗n，即

3　主要结果

定理3.1 Xn的范数是k-粗的当且仅当PXXn的范数是k-粗的.

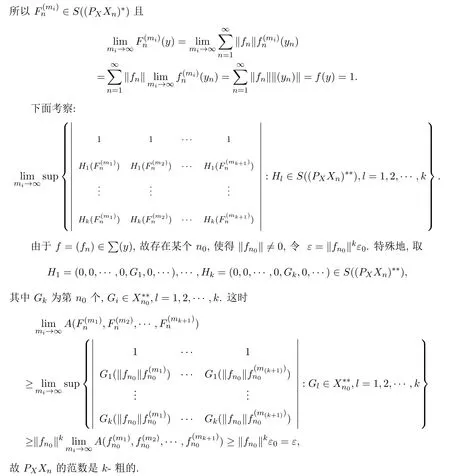
定理3.2 Xn的范数是k-强粗的当且仅当PXXn的范数是k-强粗的.

证明充分性是显然的.

定理3.3Xn的范数是k-点态粗的当且仅当PXXn的范数是k-点态粗的.

证明证法与定理3.1类似.

［1］Leach E B，Whitfield J H M.Differentiable functions and rough norms on Banach spaces［J］.Proc.A.M.S，1972，33：120-126.

［2］John K，Zizler V.On rough norms on Banach spaces［J］.Comment.Math.Univ.Carolinae，1978，19：335-349.

［3］Godini G.Rough and strongly rough norms on Banach spaces［J］.Proc.of the Amer.Math.Soc.，1983，87：239-245.

［4］义徳日胡，苏雅拉图.Banach空间范数的k-点态粗性和k-粗性［J］.纯粹数学与应用数学，2012，28（4）：553-558.

［5］义徳日胡，苏雅拉图，李婷婷.Banach序列空间的范数粗性［J］.宝鸡文理学院学报：自然科学版，2012，3（8）：6-9.

［6］Partington J R.On the Banach-Saks property［J］.Proc.Cambridge Philos.Soc.，1977，82：369-374.

［7］束立生，王建华.置换空间的一些性质［J］.南京大学学报：数学半年刊，1994，11（1）：50-58.

The k-roughness on substitution space PXXn

Qin Xuan，Suyalatu

（College of Mathematics Sscience，Inner Mongolia Normal University，huhhot 010022）

Based on the method of Banach space theory，the lifting results of k-roughness and k-strongly roughness from Banach space Xnto substitution space PXXnare researched mainly.These two k-roughness are improved on substitution space PXXn.

substitution space，k-rough norm，k-strongly rough norm，k-pointwise rough norm

O178

A

1008-5513（2015）05-0518-07

10.3969/j.issn.1008-5513.2015.05.012

2015-05-09.

国家自然科学基金（11561053）；内蒙古师范大学人才工程基金（RCPY-2-2012-K-034）.

秦璇（1991-），硕士生，研究方向：Banach空间理论.

2010 MSC:46B25