一类分数阶奇异微分方程积分边值问题正解的存在性

王晓，刘锡平，邓雪静

（上海理工大学理学院，上海200093）

一类分数阶奇异微分方程积分边值问题正解的存在性

王晓，刘锡平，邓雪静

（上海理工大学理学院，上海200093）

研究一类具有Riemann-Liouville导数的分数阶奇异微分方程积分边值问题的可解性.运用Guo-Krasnoselskii不动点定理，得到了奇异微分方程积分边值问题正解的存在性定理.最后，给出了一个实例，用于说明所得结论的有效性.

分数阶奇异微分方程；积分边值问题；正解；不动点定理

1　引言

近年来，分数阶微分方程广泛地出现在现代科学研究与技术的各个领域，其理论研究备受关注［1］.由于在实际问题中常常遇到非线性项奇异的情况，因此，国内外学者对奇异微分方程的边值问题进行了大量研究（见参考文献［2-9］）.文献［8］研究了非线性分数阶微分方程满足边值条件u（0）=u（1）=u′（0）=u′（1）=0的边值问题，分别在奇异和非奇异情况下，得到了边值问题具有多个正解的存在性定理.

本文研究一类非线性奇异分数阶微分方程

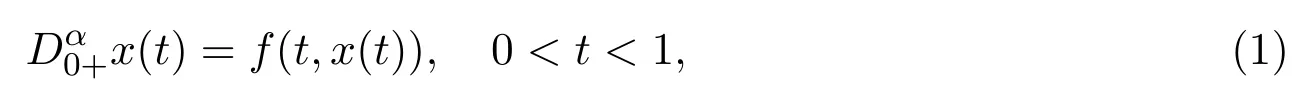
满足积分边界条件的非局部边值问题正解的存在性，其中3＜α≤4，f是一个非负函数且f（t，x）可以在x=0处奇异，g1，g2∈L1［0，1］，Dα0+是标准的Riemann-Liouville分数阶导数.运用Guo-Krasnoselskii不动点定理，得到了奇异积分边值问题正解的存在性定理.

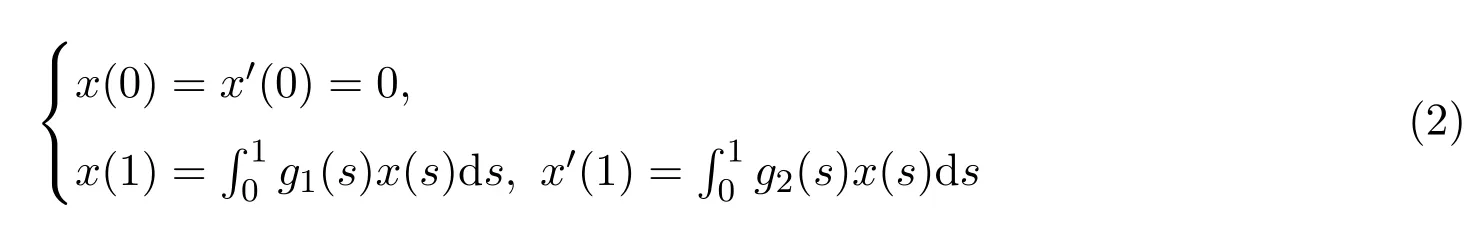
设函数f在［0，1］×（0，+∞）上有定义，且满足：

1）对几乎处处的t∈［0，1］，f（t，·）：（0，+∞）→［0，+∞）连续；

2）对所有的x∈（0，+∞），f（·，x）：［0，1］→［0，+∞）可测；

3）对任意r＞0，存在函数φr∈L1［0，1］，使得当0＜x≤r时，对几乎处处的t∈［0，1］，有0≤f（t，x）≤φr（t）.则称f在［0，1］×（0，+∞）上满足Carath é odory条件，记作f∈Car（［0，1］×（0，+∞））.

2　预备知识及引理

有关分数阶导数，分数阶积分的定义及性质请参见文献［1-2］.

引理2.1（Guo-Krasnoselskii定理［2，10］）设X为实赋范线性空间，K⊂X是锥，Ω1，Ω2⊂ K为非空相对开集，且设F：Ω2→K为全连续算子，满足：

1）‖F（x）‖≤‖x‖，∀x∈∂Ω1；‖F（x）‖≥‖x‖，∀x∈∂Ω2，或

2）‖F（x）‖≥‖x‖，∀x∈∂Ω1；‖F（x）‖≤‖x‖，∀x∈∂Ω2.则F在上存在不动点.

下面考虑满足边界条件（2）的分数阶线性微分方程

由函数G（t，s）的定义（5）容易证明下面的引理成立.

引理2.3函数G（t，s）满足如下性质：

1）G（t，s）＞0，t，s∈（0，1）；

2）（α-2）q（t）k（s）≤Γ（α）G（t，s）≤M0k（s）≤M0，t，s∈［0，1］；

3）G（t，s）在（t，s）∈［0，1］×［0，1］上连续.

3　奇异积分边值问题正解的存在性

令P=｛x∈C［0，1］：x（t）≥0，t∈［0，1］｝，则P是C［0，1］中的锥，记表示L1［0，1］上的范数.

引理3.1设条件（H0）成立，则算子A具有如下性质：

1）A是有界线性算子；

2）A（P）⊂P；

3）I-A可逆；

引理3.2假设条件（H0），（H1）成立，则Φn：Pδ→Pδ为全连续算子.

定理3.1假设条件（H0），（H1）成立，则边值问题（2）-（8）至少存在一个正解xn∈P0.

下面讨论奇异边值问题（1）-（2）正解的存在性.

定理3.2若条件（H0），（H1）成立，则边值问题（1）-（2）至少存在一个正解.

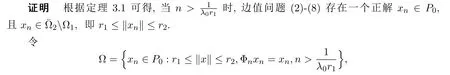
4　应用举例

本节应用前面所得到的结论，讨论一个具体的奇异分数阶微分方程边值问题.

由定理3.2知，边值问题（10）至少存在一个正解.

［1］Kilbas A A，Srivastava H M，Trujillo J J.Theory and Applications of Fractional Differential Equations［M］.Amsterdam：Elsevier B.V，2006.

［2］白占兵.分数阶微分方程边值问题理论及应用［M］.北京：陕科学技术出版社，2012.

［3］张立新，王海菊.含积分边界条件的分数阶微分方程边值问题的正解的存在性［J］.纯粹数学与应用数学，2013，29（5）：450-457.

［4］Liu Xinping，Wu Guiyun.Existence of positive solutions for integral boundary value problem of fractional differential equations［J］.Journal of Shanghai Normal University：Natural Sciences：Mathematics，2014，43（5）：496-505.

［5］刘帅，贾梅，秦小娜.带积分边值条件的分数阶微分方程解的存在性和唯一性［J］.上海理工大学学报，2014，36（5）：409-415.

［6］金京福，刘锡平，窦丽霞，等.分数阶积分微分方程边值问题正解的存在性［J］.上海理工大学学报，2011，49（5）：824-828.

［7］Bai Zhanbing，Sun Weichen.Existence and multiplicity of positive solutions for singular fractional boundary value problems［J］.Computers and Mathematics with Applications，2012，63（9）：1369-1381.

［8］Xu Xiaojie，Jiang Daqing，Yuan Chengjun.Multiple positive solutions for the boundary value problem of a nonlinear fractional differential equation［J］.Nonlinear Analysis TMA，2009，71（10）：4676-4688.

［9］Agarwal R P，O′Regan D，Stanek S.Positive solutions for Dirichlet problems of singular nonlinear fractional differential equations［J］.J.Math.Anal.Appl.，2010，371（1）：57-68.

［10］郭大钧，孙经先，刘兆理.非线性常微分方程泛函方法［M］.济南：山东科学技术出版社，2006.

The existence of positive solutions for a class of fractional singular differential equations with integral boundary conditions

Wang Xiao，Liu Xiping，Deng Xuejing

（College of Science，University of Shanghai for Science and Technology，Shanghai200093，China）

This paper investigates the solvability for a class of fractional singular differential equations involving the Riemann-Liouville fractional derivative with integral boundary conditions.By means of Guo-Krasnoselskii fixed point theorem，the existence theorems of positive solutions for the boundary value problem are established.Finally，an example is presented to illustrate the main results.

fractional singular differential equation，integral boundary value problem，positive solution，fixed point theorem

0175.8

A

1008-5513（2015）05-0509-09

10.3969/j.issn.1008-5513.2015.05.011

2015-03-01.

国家自然科学基金（11171220）；沪江基金（B14005）.

王晓（1989-），硕士生，研究方向：常微分方程理论与应用.

刘锡平（1962-），硕士，教授，研究方向：常微分方程理论与应用.

2010 MSC:34B08，34B18，26A33