基于刚柔耦合模型的泵车臂架动力学仿真与优化

王 玮，李 红，骆 群，周明华，李新松

（扬州大学机械工程学院，江苏 扬州225127）

基于刚柔耦合模型的泵车臂架动力学仿真与优化

王 玮，李 红*，骆 群，周明华，李新松

（扬州大学机械工程学院，江苏 扬州225127）

为使混凝土泵车臂架系统的计算机仿真模型更好地体现实际情况，根据机器人运动学理论和拉格朗日方程，通过递推形式确定了混凝土泵车柔性臂架系统的动力学方程，并运用计算机联合仿真技术对混凝土泵车臂架系统进行柔性仿真，同时优化了臂架系统上的驱动力，结果显示不断改变铰点位置能明显降低变幅机构中油缸的最大受力数值.仿真结果表明，柔性臂架模型更符合实际情况，为混凝土泵车臂架改进设计和机器人化提供了理论依据.

混凝土泵车；臂架系统；动力学仿真；刚柔耦合；油缸驱动力

混凝土泵车是一种通过液压系统带动多节可折叠臂架旋转，同时臂架带动输料管运动且可连续、均匀泵送混凝土到指定位置进行浇注的专用车辆［1］.使用混凝土泵车能有效缩短建筑工期，减少劳动消耗.混凝土泵车臂架系统采用多冗余度悬臂梁结构，在其工作过程中，臂架不可避免地产生振动.通过建立臂架系统合理模型，并研究臂架末端的运动轨迹或通过软件仿真臂架的运动过程［2-3］，可获得降低臂架振动的方法.本文通过研究臂架动力学方程来揭示臂架的各项动力学特性，分析模型运动学和动力学，优化了末节油缸驱动力，为今后改进臂架系统设计提供参考.

1　混凝土泵车柔性臂架的动力学方程

将机器人运动学理论应用于泵车臂架系统中，把液压缸视为滑块，带动各节臂架实现回转.回转台坐标系逆向动力学分析的解具有唯一性，所以在建立整节臂架系统方程时，只须计算臂架系统各杆件弹性变形的运动学方程及各杆件之间的夹角，而无须考虑回转台运动学的影响，故臂架系统的运动可转化为平面运动.运用第二类拉格朗日方程及相关理论，通过建立递推式可得到该系统的动力学方程.首先研究2节臂架系统［4］，建立臂架系统动力学方程，然后将此方程推广到多节臂架系统，为泵车臂架系统建模提供理论依据.

1.1臂架上任一点的位置、速度及加速度

在臂架系统所在平面上建立一个全局坐标系x Oy（见图1），采用随柔性体形变而变化的浮动坐标系.若一柔性体从某一个地点运动到另一地点，则其整体运动可分解为刚性移动、刚性转动和变形运动.像刚性体臂架一样，假设P为第2节柔性臂上任意一点，其位置向量为rP=r0+A（sP+uP），其中r0为浮动坐标系的原点在惯性坐标系中的向量，rP为P点在惯性坐标系中的向量，sP为未变形时柔性第2节臂架上P点在浮动坐标系中的向量，uP为柔性体的相对变形向量，A为旋转变换矩阵.

图1　两节臂架模型示意图Fig.1 Schematic of two booms

采用模态坐标对点P的单元变形可描述为uP=ΦPq，式中q为变形的广义坐标，ΦP为点P满足里兹基向量要求的假设变形模态矩阵.依据位置向量对时间一阶和二阶导数求得柔性臂架上P点的速度和加速度为

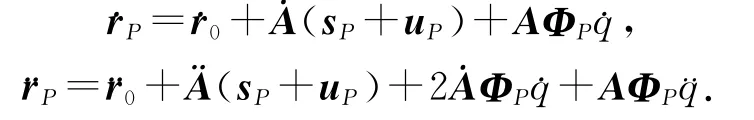
1.2臂架系统的能量

考虑到第2节臂架末端具有集中质量m2，取其等效密度ρ2′=ρ2+m2δ（x2-l2），ρ2为均质臂架单位长度的质量，m2δ（x2-l2）表示臂架末端质量的分布密度，对体积V积分可得第2节柔性臂架动能，式中mP和IP分别是点P的节点质量和节点惯性张量；ωP为点P相对于全局坐标基的角速度在局部坐标基中的斜方阵表示；势能为W=Wg（ξ）+2-1ξTHξ，其中H 为弹性势能中结构件的广义刚度矩阵，ξ为广义坐标，因而，弹性应变能与臂架整体刚性运动无关，通常为常量.

1.3臂架系统的动力学方程

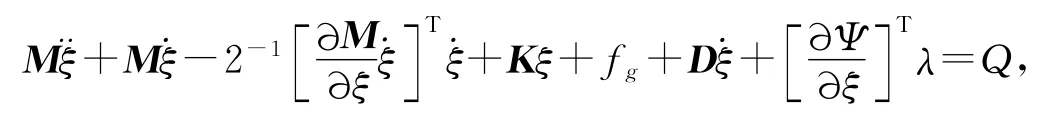
式中K，M，D分别为模态刚度矩阵、质量矩阵和模态阻尼矩阵；，Kξ分别为柔性体内因阻尼和弹性变形引起的广义力；fg为广义重力；Q为广义外力.

2　混凝土泵车刚柔耦合模型建立与验证

2.1混凝土泵车刚柔耦合模型建立

利用ANSYS软件生成臂架系统模态中性文件，并在ADAMS泵车臂架刚性模型中依次读入各节臂架的MNF文件.为了便于分析，在选定要替换的刚性体同时载入对应的柔性体，ADAMS软件便会对柔性体自动定位.替换成功后，原刚性体的运动形式、负荷及驱动力等都转换到柔性体上，且柔性体会保持原刚性体的名称和初始速度等特征［5］，最终得到整个臂架系统的刚柔耦合模型，见图2.

图2　臂架系统刚柔耦合模型Fig.2 Rigid and flexible model of boom system

2.2刚柔耦合模型的验证

刚柔耦合模型的建立过程中存在ADAMS与ANSYS软件间数据转换，进行动力学仿真之前，必须保证信息传递的准确性，否则仿真后处理结果毫无意义.模态中性文件的验证可从以下3个方面分析：①使用ADAMS中的Info功能检查柔性体的物理特性，包括质量、质心位置以及转动惯量；②比较模型的模态信息，利用ADAMS/Linear模块与有限元模态分析结果进行比较；③对柔性体进行仿真，并测量节点的静力变形量或应力值，比较其最大值与相同约束条件下有限元分析的结果［6］.

以第1节臂架为例进行模态中性文件的验证.打开第1节臂架的柔性体信息，与相应刚性体比较发现，质心位置重合，质量和转动惯量相差很小.采用ADAMS/Linear模块，在不考虑阻尼状态下，比较第1节臂架柔性体的固有频率与ANSYS中的模态分析结果（见表1）.通过验证发现，在相同约束条件下，臂架模型的ANSYS模态分析结果与ADAMS线性分析结果近似相等，说明模态中性文件是正确的，可利用臂架系统刚柔耦合模型作进一步的仿真研究.

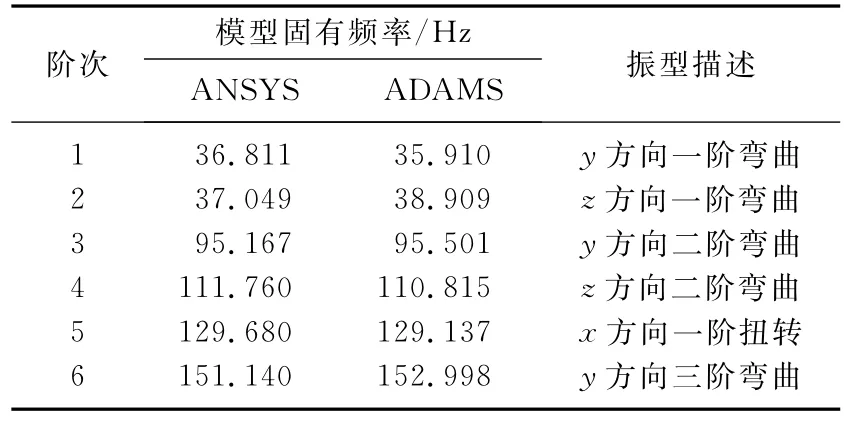
表1　第1节臂架固有频率Tab.1 Natural frequency of boom 1

3　混凝土泵车刚柔耦合模型优化

对验证后的臂架系统刚柔耦合模型进行运动学和动力学仿真分析［7］.图3，4为模型第5节臂架位移仿真结果.由图可见，大范围刚体运动和局部弹性变形引起的耦合效应可使臂架系统出现一定程度的弹性变形，且臂架末端受到叠加影响，振动现象尤为明显.这种现象对于轻质长臂杆类泵车臂架系统来说是无法避免的，只能采取一些减振措施尽量减小振动带来的负面影响.

图3　第5节臂架末端点纵向位移曲线Fig.3 Longitudinal displacement curve of boom 5

图4　第5节臂架末端点横向位移曲线Fig.4 Transverse displacement curve of boom 5

对臂架系统刚柔耦合模型仿真后发现，臂架末端振动最明显，油缸受力也比较复杂.选取油缸5作为研究对象，对油缸受力进行优化.首先，对臂架油缸5处的铰接点、连杆连接点等位置进行参数化处理，如图5所示.

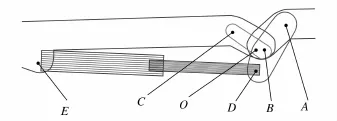
图5　臂架4与臂架5间各铰点Fig.5 Parametric name of hinge points between boom 4 and 5

创建设计变量v1，v2，…，v10代替铰链位置的坐标，各点坐标为A（v1，v2），B（v3，v4），C（v5，v6），D（v7，v8），E（v9，v10）.理论上，应把10个参数全部作为设计变量进行优化设计，但在此空间中寻求最优解计算量巨大，效率极低；因此，在优化迭代前，先选用灵敏度对设计变量进行分析，过滤灵敏度值低的变量［8-9］.结果显示，v3，v6，v7，v8在初始位置时的灵敏度值较其他变量高，意味着它们对臂架系统变幅机构影响较大；因此，选用v3，v6，v7，v8对油缸5受力影响较大的变量进行优化设计，从而找到使油缸5最大受力减小时各铰点的坐标值.

图6为第5节臂架油缸受力的优化曲线，可见曲线在横轴上下不规则地跳动，说明油缸受力非常复杂.在第5节臂架回收过程中，由于轻质长杆存在振动，必然导致油缸受力不稳定，在臂架回收接近终点时图像振荡幅度减弱，说明油缸受力已趋于稳定.这是由于第5节臂架在接近收拢时，油缸5与第5节臂架处于坐标系原点同侧，力臂减小，因而第5节臂架振动幅度减弱，油缸受力趋于平缓.优化后的油缸受力基本小于优化前的受力，而且通过多次改变变幅机构中铰点坐标值，使得油缸5在最大受力工况下的最大受力值逐渐降低［10］，最终由438 kN减小到286 kN，减幅达34.6%.通过多次改变变幅机构中铰点的坐标值，可达到减小油缸最大受力的效果，且为了避免因改变铰点位置而使系统内发生干涉现象，铰点坐标的优化幅度为0.3%～2.3%（见表2）.

表2　优化前后设计变量的比较Tab.2 Comparison of design variables during optimization

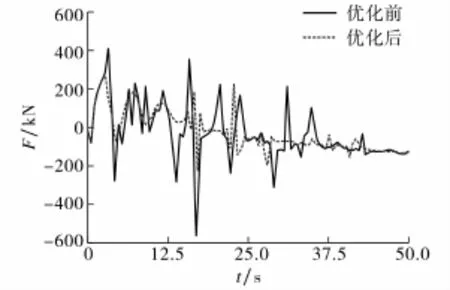
图6　油缸5受力优化曲线Fig.6 Optimization curve of oil cylinder 5

［1］LIN Peichun，WANG Jenhun，HUANG Shanhun，et al. Dispatching ready mixed concrete trucks under demand postponement and weight limit regulation［J］.Automat Constr，2010，19（6）：798-807.

［2］陈栋，王刚，谢秀芬.混凝土泵车臂架振动的动态特性 ［J］.机械设计与研究，2011，27（4）：92-95.

［3］戴丽.基于柔性多体动力学的混凝土泵车臂架系统的建模与仿真 ［D］.沈阳：东北大学，2007.

［4］WONG K V，BARIN E.Oil spill containment by a flexible boom system［J］.Spill Sci Technol B，2003，8（5）：509-520.

［5］冯波.混凝土泵车臂架系统的仿真分析 ［D］.长沙：长沙理工大学，2012.

［6］朱大炜.基于模态综合法的雷达天线机构的柔体动力学仿真 ［D］.上海：上海交通大学，2007.

［7］CAZZULANI G，GHIELMETTI C，GIBERTI H，et al.A test rig and numerical model for investigating truck mounted concrete pumps［J］.Automat Constr，2011，20（8）：1133-1142.

［8］YAN Shangyao，LAI Weishen，CHEN Maonan.Production scheduling and truck dispatching of ready mixed concrete［J］.Transport Res E，2008，44（1）：164-179.

［9］姚菁琳，郑翔，张新国.八连杆压力机传动系统的设计及优化 ［J］.扬州大学学报：自然科学版，2014，17（1）：46-49.

［10］SONG Ping，LI Qingzhou，LI Keiie.Sensitivity optimization of a monolithic high-shock three-axis piezoresistive accelerometer with single sensing element［J］.Chin Sci Bull，2009，54（19）：3600-3607.

Dynamics simulation and optimization of the boom system of the concrete pump truck based on rigid and flexible model

WANG Wei，LI Hong*，LUO Qun，ZHOU Minghua，LI Xinsong
（Sch of Mech Engin，Yangzhou Univ，Yangzhou 225127，China）

Combining with the theories of robotics and Lagrange’s equation，a dynamical function for flexible boom of concrete pump truck is established by the recurrence methods in order to make the computer model better reflect the actual situation.Based on the dynamical function，the rigid and flexible model of concrete pump truck is built and simulated through the ioint application of ANSYSand ADAMS.Using the rigid and flexible mode of boom system，the cylinder stress of luffing mechanism are studied by using optimization module after verifying the accuracy of dynamic model.It is found from the simulation results that the rigid and flexible model provides a theoretical basis for truck improvement and robotizing.

concrete pump truck；boom system；dynamics simulation；rigid and flexible；cylinder stress

TU 646

A

1007-824X（2015）01-0061-04

（责任编辑 贾慧鸣，秋 实）

2013-10-16.*联系人，E-mail：lhchina@163.com.

国家科技部火炬计划资助项目（2012GH530716）.

王玮，李红，骆群，等.基于刚柔耦合模型的泵车臂架动力学仿真与优化［ J］.扬州大学学报：自然科学版，2015，18（1）：61-64.