基于Hv估计的随机振动功率谱复现控制算法
2015-10-17徐金城郝连奎
徐金城,谢 勇*,陈 立,郝连奎
(1.扬州大学信息工程学院,江苏 扬州225127;2.江苏东华测试股份有限公司,江苏 靖江214500)
基于Hv估计的随机振动功率谱复现控制算法
徐金城1,谢 勇1*,陈 立2,郝连奎2
(1.扬州大学信息工程学院,江苏 扬州225127;2.江苏东华测试股份有限公司,江苏 靖江214500)
针对传统的基于H1估计的随机振动控制算法估计系统频响函数时的不足,提出一种基于Hv估计的频响函数修正算法.首先在试验初始阶段采用Hv估计法估计系统频响函数,然后对其进行迭代修正,以减小系统时变特性的影响,使得估计结果更加接近真实频响,最后通过功率谱复现仿真验证了该文方法的有效性.
随机振动;Hv估计;迭代修正;功率谱复现
电子设备在工作环境中的振动多为随机振动,其使用的可靠性与稳定性检验显得尤为重要[1-2].随机振动的特性常通过功率谱或功率谱密度(power spectral density,PSD)来描述,因此如何提高随机振动功率谱复现试验的控制精度和效率已成为国内外研究的重点.Mao等[3]探讨了基于H1估计的传统功率谱复现试验法,但因忽略了振动台系统输入端的噪声和系统中时变、非线性成分的影响,故控制精度和控制效率偏低.崔旭力等[4]采用Hv估计法有效地提高了振动系统初始频响函数估计的精确性;Daley[5],Guan[6]等分别采用控制驱动谱迭代步长法以及自适应逆控制法弥补了试验过程中初始频响函数估计的缺陷,虽然提高了控制效率,但均未考虑振动台系统中的时变和非线性成分的影响,且未对频响函数进行相应的修正.本文提出一种基于Hv估计的频响函数迭代修正算法,在试验过程中实时修正系统频响函数,并采用智能迭代法修正驱动谱,以期减小系统时变特性的影响,从而提高控制的精度和效率.
1 本文算法
1.1频响函数估计与修正
假设系统输入向量为x(f),输出向量为y(f),定义误差向量

将式(1)两端同时右乘e(f)的共扼转置e(f)H,取期望值

令Gee=E[e(f)e(f)H],并改写成矩阵形式:
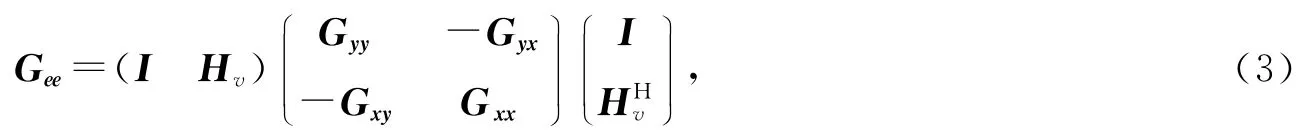
式中Gxy(f),Gyx(f)分别为系统输入信号与输出信号、输出信号与输入信号的互功率谱密度均值,Gxx(f),Gyy(f)分别为系统输入信号和输出信号的自功率密度均值,I为单位矩阵.
根据误差谱矩阵的对角线元素之和最小的原则[7],确定单输入单输出系统的Hv估计计算式:
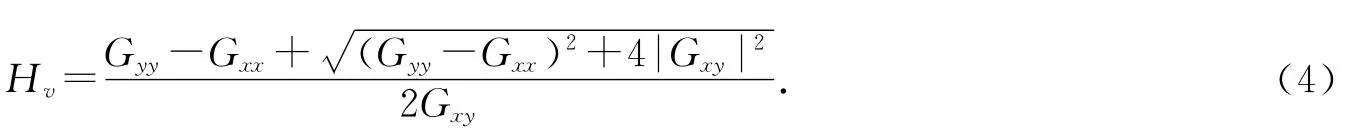

其中μ为修正系数,0<μ<1.
1.2驱动谱修正及驱动信号的生成
记试验参考谱为R(f),定义第i次迭代控制后的误差谱
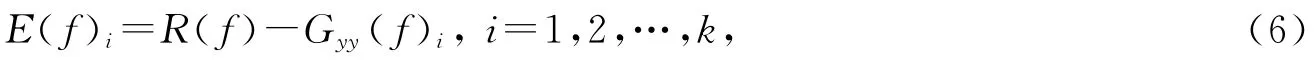
对驱动谱进行智能迭代[8]修正:

式中Gxx(f)i+1为第i+1次修正后的驱动信号功率谱密度均值,β为可变的迭代步长,0.1≤β≤0.5,Z(f)i为第i次频响修正后的系统阻抗.
修正后的驱动谱经时域随机化处理[9]可得到时域随机驱动信号.
1.3功率谱复现控制算法的实现步骤
1)根据式(4)估计系统初始频响函数H(f)0;
2)计算系统初始阻抗Z(f)0=1/H(f)0,取模|Z(f)0|,根据式(7)计算初始驱动谱,生成初始驱动信号;
3)实时采集系统输入输出信号,计算输入输出自功率谱密度均值和互功率谱密度均值[10],根据式(5)计算修正后的频响H(f)i,更新系统阻抗Z(f)i=1/H(f)i,取模|Z(f)i|;
4)根据式(6)计算误差谱,式(7)修正驱动谱,并生成时域驱动信号重新驱动振动台.
本文算法的实现过程如图1所示.
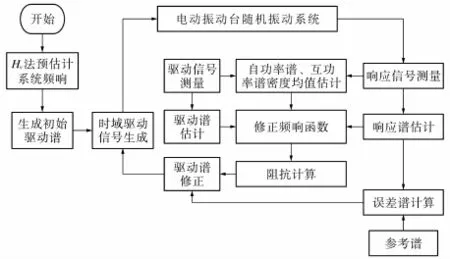
图1 本文算法的实现示意图Fig.1 Principle figure of the algorithm of this paper
2 仿真结果与分析
为了验证本文算法的有效性,笔者应用Matlab软件分别在未加算法、基于H1估计的传统算法及本文算法控制的3种情况下进行随机振动功率谱复现对比试验,结果如图2~4所示.仿真所用振动台传递函数模型[11]的空载定电压幅相特性如图5所示.系统输入输出端的噪声干扰采用白噪声模拟,且为了增强可比性,各算法的仿真参数设置相同.
由图2~4可见,未使用控制算法的功率谱复现仿真结果大大超出了试验的停止限(±6 dB);采用H1估计法进行驱动谱修正数次后,复现谱在共振点处仍有超差,波动也较大,若要进一步提高控制精度,仍须继续进行修正试验,导致试验的调节时间增长;而本文算法明显优于H1估计法,其复现谱已完全控制在容差限(±3 dB)内,且波动小,能满足试验的控制精度要求.

图2 未进行控制的复现结果Fig.2 Simulation results without control

图3 基于H1估计的复现结果Fig.3 Simulation results based on H1estimator
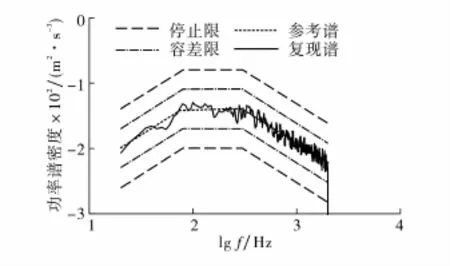
图4 本文算法的复现结果Fig.4 Simulation results based on this paper

图5 振动台模型的幅相特性Fig.5 Magnitude-phase characteristics of electro-dynamic vibration shaker
[1]XIE Haiiun,ZHOU Deiian,LIU Zhengwei.The sub-model method for analysis of BGA ioint stress and strainduring random vibration loading[C]//International Conference on Electronic Packaging Technology&High Density Packaging.Guilin,China:IEEE,2012:1216-1221.
[2]YU D,AL-YAFAWI A,PARK S,et al.Finite element based fatigue life prediction for electronic components under random vibration loading[C]//Proceedings of Electronic Components and Technology Conference.Las Vegas,NV,USA:IEEE,2010:188-193.
[3]MAO Z,TOOD M.Statistical modeling of frequency response function estimation for uncertainty quantification[J].Mech Syst Sign Process,2013,38(2):333-345.
[4]崔旭力,陈怀海,贺旭东,等.全相位Hv频响函数估计在MIMO随机振动试验控制中的应用[J].振动工程学报,2011,24(2):181-185.
[5]DALEY S,OWENS D H,HATONEN J.Appllication of optimal iterative learning control to the dynamic testing of mechanical structures[J].J Syst Control Eng,2007,221(2):211-222.
[6]GUAN Guangfeng,XIONG Wei,WANG Haitao.Random vibration control based on adaptive filter[C]//Proceedings of the International Conference on Mechatronics and Automation.Xi’an:IEEE,2010:1825-1830.
[7]杨志东,关广丰,丛大成,等.基于Hv方法的三轴液压振动系统频响函数估计研究[J].地震工程与工程振动,2007,27(3):83-87.
[8]TSUI K M,CHAN S C.Iterative correction of frequency response mismatches in time-interleaved ADCs:A novel framework and case study in OFDM systems[J].Green Circuits Syst,2010,8(21):253-258.
[9]GUAN Guangfeng,XIONG Wei,WANG Haitao.Adaptive control of random vibration test system[C]//International Conference on Intelligent Control and Information Processing.Dalian:IEEE,2010:149-153.
[10]AKCAY H.Spectral estimation in frequency-domainby subspace techniques[J].Signal Process,2014,101:204-217.
[11]周远方.虚拟振动环境试验[D].北京:北京航空航天大学,2002.
Power spectral density control algorithm of random vibration based on Hvestimator
XU Jincheng1,XIE Yong1*,CHEN Li2,HAO Liankui2
(1.Sch of Inf Engin,Yangzhou Uinv,Yangzhou 225127,China;2.Jiangsu Donghua Test Co Ltd,Jingiiang 214500,China)
Aiming at the shortage of the H1FRF(frequency response function)estimators used in the traditional random vibration control system,an iterative correction algorithm based on Hvestimator is put forward.By using Hvestimator to estimate the system FRF in the initial stage and correcting the FRF during the process,the method reduces the time-varying effect of the system and improves the control precision.The power spectral density replication simulation results show that the algorithm is better than the traditional method in control precision and control efficiency.
random vibration;Hvestimation;iterative correction;power spectral density replication
O 324;TP 271.9
A
1007-824X(2015)01-0013-03
(责任编辑 林 子)
2014-03-18.*联系人,E-mail:yzxieyong@126.com.
国家自然科学基金资助项目(61174046).
徐金城,谢勇,陈立,等.基于Hv估计的随机振动功率谱复现控制算法[J].扬州大学学报:自然科学版,2015,18(1):13-15,56.
