一类多叶解析函数的若干性质
2015-10-17李慧珍
李慧珍,韩 悦
(扬州大学数学科学学院,江苏 扬州225002)
一类多叶解析函数的若干性质
李慧珍*,韩 悦
(扬州大学数学科学学院,江苏 扬州225002)
利用微分从属的方法并通过限制一些定义条件,定义了一个新的多叶解析函数类Tλ,α,p(M,N),同时根据微分从属的部分结论导出Tλ,α,p(M,N)内函数的从属关系、半径问题等性质.
多叶解析函数;微分从属;超几何函数
在复分析中,有关解析函数类和微分从属的研究已经取得了诸多重要成果.Liu[1],Mahzoon[2]等对某类多叶解析函数类微分从属的最佳控制函数和包含关系进行了分析探讨.刘文娟[3],Wang[4],Ibrahim[5]等运用不同的算子构造出新的多叶解析函数子类并分析了它们的性质.Srivastava[6],Tang[7]等分析探讨了微分从属性质的相关应用.Singh[8],Praiapat[9]等利用微分从属理论研究了解析函数类的一些性质.近年来,许多学者运用微分从属的方法来定义新的解析函数类,如Praiapat等[10]利用微分从属定义了单位圆U内的解析函数类,并得到该函数类的多个性质与结论.受此启发,本文拟运用微分从属的方法定义单位圆U内一个新的多叶解析函数类,并探讨该函数类的从属关系及半径问题等.
1 预备知识
本文中Ap表示形如

且在单位圆U={z∈C:|z|<1}内解析的全体函数的集合,其中p∈N+.
定义1 若函数f(z)属于多叶解析函数类Tλ,α,p(M,N),则f(z)满足f(z)∈Ap且

其中λ>0,α>0,-1≤N<M≤1,p∈N+.
引理2 设φ(z)=1+a1z+a2z2+…在单位圆U内解析,h(z)是U内的凸函数,h(0)=1,如果φ(z)+γ-1zφ′(z)≺h(z),其中Reγ≥0,γ≠0,z∈U,则

且ψ(z)为最佳控制函数.
引理3 设q(z)在单位圆U内单叶解析,θ(z)和φ(z)在D⊃q(U)内解析,且对w∈q(U),有θ(w)≠0.令Q(z)=zq′(z)φ(q(z)),h(z)=θ(q(z))+Q(z),满足如下条件:
1)Q(z)在U内是星形的;
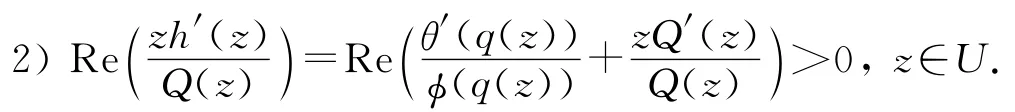
如果p(z)在U内解析,p(0)=q(0),p(U)⊂D且θ(p(z))+zp′(z)φ(p(z))≺θ(q(z))+ zq′(z)φ(q(z))=h(z),则p(z)≺q(z),q(z)为最佳控制函数.
引理4 对于复数a,b,c(c≠0,-1,-2,…),有

2 主要结果
定理5 若f(z)∈Tλ,α,p(M,N),则
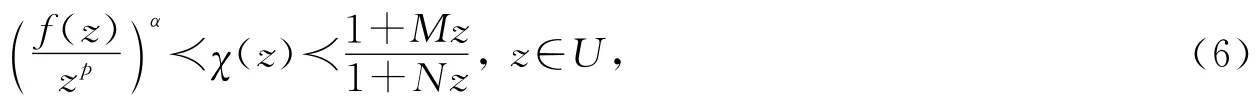
其中

χ(z)为式(6)的最佳控制函数,且

是精确的.
证明 设函数f(z)∈Tλ,α,p(M,N),且

则p(z)=1+αap+1z+…在单位圆U内解析,p(0)=1.对式(9)关于z求导并计算可得
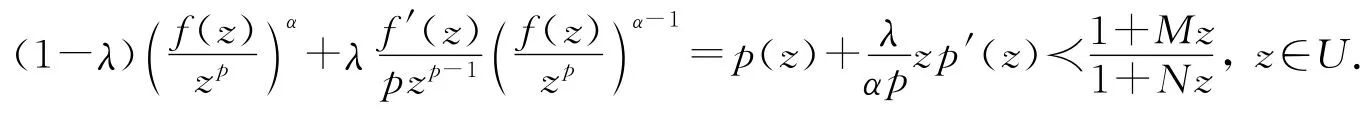
根据引理1及式(4)(5)可得
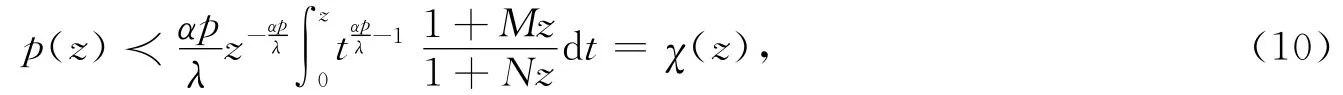
χ(z)为式(6)的最佳控制.
定理6 若f(z)∈Ap且满足不等式

其中z∈U,α>0,0≤ρ<1,p∈N+,则
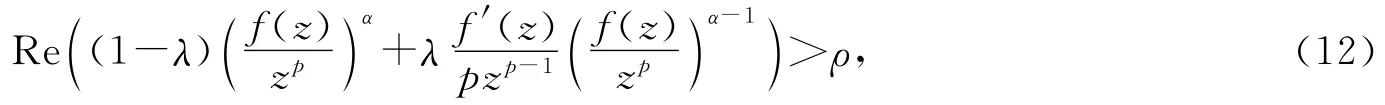
其中|z|<R1,λ>0,且是精确的.
证明 设f(z)∈A且满足式(11),有

其中w(z)=1+a1z+a2z+…在U 内解析且有正实部.对式(13)关于z求导可得


当|z|<R1时,式(15)右边为正,即f(z)∈Tλ,α,p(1-2ρ,-1).又因f(z)∈Ap满足(f(z)/zp)α=ρ+(1-ρ)(1-z)/(1+z),故当z=R1时,有,从而边界R1是精确的.
定理7 设f(z)∈Tλ,α,p(M,N),定义I(f):Ap→Ap使得
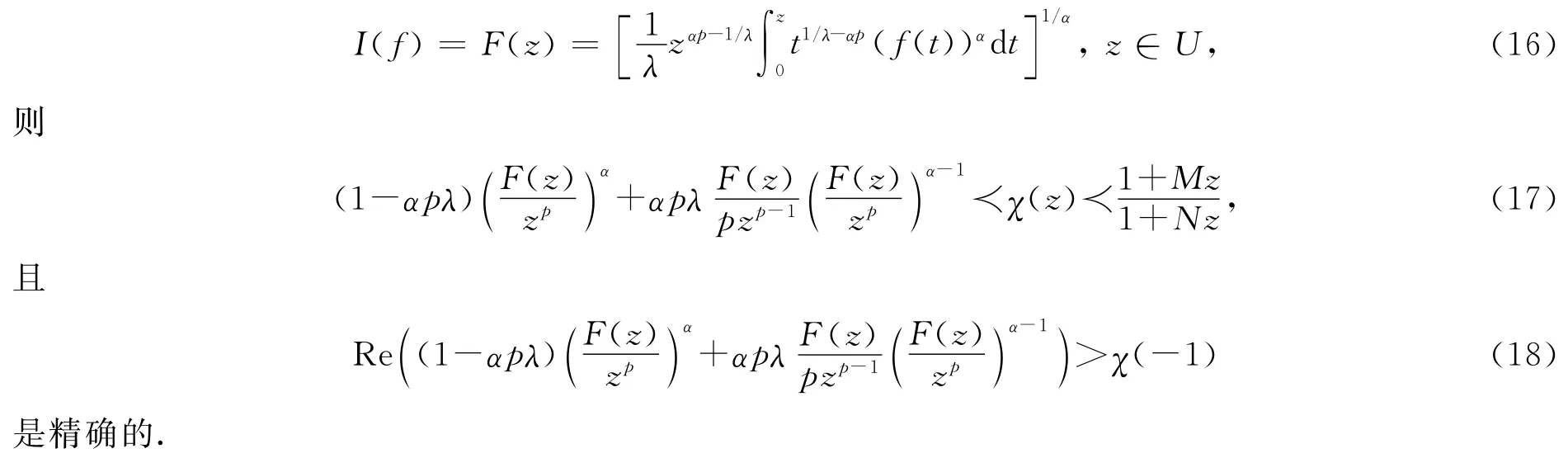
证明 设f(z)∈Tλ,α,p(M,N),对式(16)左右两边关于z 求导,可得,进而结合定理5得证.
定理8 设f(z)∈Ap,z∈U,-1<M<1,
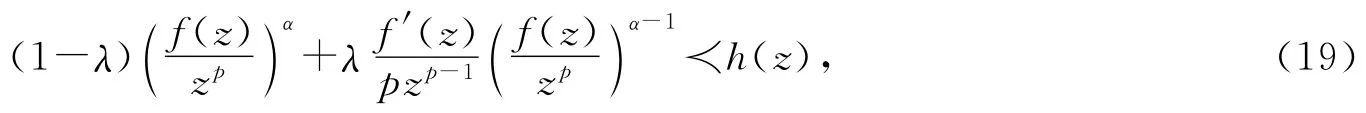
证明 由p(z)=(z-pf(z))α,式(19)可转化为

取q(z)=(1+Mz)/(1-z),θ(w)=w,φ(w)=λ/(αp),其中q(z)在U内解析,q(0)=1,θ(w)和φ(w)在C/{0}内解析,θ(w)≠0,可得而Q(z)在U内为星形单叶是由于,进一步地,,z∈U,所以有,即h(z)为近于凸函数.据式(20)可知θ(p(z))+zp′(z)φ(p(z))≺θ(q(z))+zq′(z)φ(q(z)).综上所述,由引理3可得p(z)≺q(z),即
[1]LIU Jinlin.Properties of certain multivalent analytic functions[J].Adv Math,2002,31(6):565-569.
[2]MAHZOON H.New subclasses of multivalent functions defined by differential subordination[J].Appl Math Sci,2012,6:93-96.
[3]刘文娟,彭娟,杨清.与Noor积分算子有关的多叶解析函数子类的性质[J].扬州大学学报:自然科学版,2012,15(3):8-11.
[4]WANG Z G,AGHALARY R,DARUS M,et al.Some properties of certain multivalent analytic functions involving the Cho-Kwon-Srivastava operator[J].Math Comput Model,2009,49(9):1969-1984.
[5]IBRAHIM R W,DARUS M.On certain classes of multivalent analytic functions[J].J Math Stat,2010,6(3):271-275.
[6]SRIVASTAVA H M,ATTIYA A A.Some applications of differential subordination[J].Appl Math Lett,2007,20(11):1142-1147.
[7]TANG H,DENG G T,LI S H.Certain subclasses of p-valently analytic functions involving a generalized fractional differintegral operator[J].J Egypt Math Soc,2014,22:36-44.
[8]SINGH S,GUPTA S.A differential subordination and starlikeness of analytic functions[J].Appl Math Lett,2006,19(7):618-627.
[9]PRAJAPAT J K,RAINA R K.Certain results on differential subordination for some classes of multivalently analytic functions associated with a convolution structure[J].Bull Belg Math Soc Simon Stevin,2009,16(1):153-165.
[10]PRAJAPAT J K,RAINA R K.Some result on certain class of analytic functions based on differential subordination[J].Bull Korean Math Soc,2013,50(1):1-10.
Properties of a certain subclass of multivalent analytic functions
LI Huizhen*,HAN Yue
(Sch of Math Sci,Yangzhou Univ,Yangzhou 225002,China)
Using the methods of differential subordination and sufficient conditions determined,the author defines a new class of multivalent analytic functions Tλ,α,p(M,N).Making use of the familiar principle of differential subordination,subordination relationship and radius problems involving the function Tλ,α,p(M,N)are derived.
multivalent function;differential subordination;hypergeometric function
O 174.5
A
1007-824X(2015)01-0009-04
(责任编辑 林 子)
2014-04-21.*联系人,E-mail:Lhzhen8959@163.com.
江苏省大学生实践创新训练计划项目(201411117037z).
李慧珍,韩悦.一类多叶解析函数的若干性质[J].扬州大学学报:自然科学版,2015,18(1):9-12.
