一个5阶图与点、路、圈联图的交叉数

李　敏

（湖北文理学院数学与计算机科学学院，湖北　襄阳441053）

一个5阶图与点、路、圈联图的交叉数

李敏

（湖北文理学院数学与计算机科学学院，湖北襄阳441053）

分别讨论了5阶图G16与nK1，Pn，Cn联图的交叉数，得到，其中n K1是n个孤立点构成的图，Pn，Cn分别是含n个点的路和圈.

5阶图；交叉数；联图；路；圈

图的交叉数概念起源于Turan的“砖厂问题”，Garey和Johnson［1］已经证明这是一个NP-完全问题.由于解决该问题的难度较大，迄今为止，能确定交叉数的图类还不多，其中小阶图与路、圈、星的笛卡尔积图是目前少数几类已知精确交叉数的图类之一［2-3］.已有联图的交叉数研究结果可见文献［4-9］.为了进一步丰富交叉数的结果，本文在前人研究的基础上，拟探讨联图G16+n K1，G16+Pn，G16+Cn的交叉数（图G16［2］358的画法如图1所示），文中所用的概念、符号及图的有关性质等与文献［6，10］一致.

图1　图G16Fig.1 The graph G16

1　联图G16+n K1的交叉数

图G16+n K1是由图G16以及n个点t1，t2，…，tn和G16的点连接而成的.记ti和G16的点连接而成的图为Ti.由图2知

命题1 设图G16+n K1（n≥3）有一个好画法D，图G16+（n-2）K1在画法D下至少有个交叉点.如果i≠j（i，j∈｛1，2，…，n｝），使得crD（Ti，Tj）=a，crD（Ti∪Tj，G16）=b，同时对任意的k≠i，j，有crD（Ti∪Tj，Tk）≥4，则图G16+n K1在画法D下至少有Z（5，n）+n+ n/2+a+b-3个交叉点.

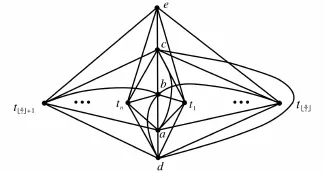
图2　图G16+n K1的一个好画法Fig.2 A drawing of G16+n K1

证明 可设crD（Ti，Tj）=a，crD（Ti∪Tj，G16）=b，同时对任意的k≠i，j，有crD（Ti∪Tj，Tk）≥4，则由图的交叉数性质可得

命题2 设图G+n K有好画法D，又存在i，对任意j≠i（i，j∈｛1，2，…，n｝），有cr（G∪Ti，

161D16Tj）≥4.若使得crD（G16∪Ti，Tj）＞4的Tj有c个，则在画法D下图G16+n K1至少有个交叉点.

命题3 设图G16+n K1有好画法D，若存在i≠j（i，j∈｛1，2，…，n｝），使得crD（Ti，Tj）=0，则crD（G16，Ti∪Tj）≥3.

证明 由D为图G16+n K1的好画法及crD（Ti，Tj）=0知，在D诱导的Ti∪Tj的子画法中Ti和Tj的边与边之间无交叉点.对任意G16的点x，含有它的区域只包含G162个不同于x的点.而由图1知，点a，b，c，d的度均不小于3，因此与这4点相连的边上至少有3个交叉点，结论成立.

证明 当n=1时，由图2知cr（G16+K1）≤1，又因K5是图G16+K1的子图，故cr（G16+K1）≥1，即有cr（G16+K1）=1.当n=2时，由图2知cr（G16+2K1）≤3.下面证明反向不等式cr（G16+ 2K1）≥3.可证G16（在同构意义下）只有如图3所示的7种画法.若存在Ti（i=1，2），满足crD（G16，Ti）=0，则G16∪Ti只有如图4所示的2种画法，可证无论tj落入何区域，均有crD（G16∪Ti，Tj）≥3.若对任意的Ti，有crD（G16，Ti）≠0，则crD（G16，T1∪T2）≥2.如果crD（T1，T2）=0，则由命题3知crD（G16，T1∪T2）≥3；如果crD（T1，T2）≠0，则crD（T1∪T2）≠0.又因crD（G16+2K1）=crD（G16∪T1∪T2）=crD（G16）+crD（G16，T1∪T2）+crD（T1∪T2），故在上述几种情形下都有cr（G16+2K1）≥3，即结论成立.

图3　图G16在同构意义下的所有画法Fig.3 The drawings of G16in the isomorphism sense

情形1：有Ti和Tj，满足crD（Ti，Tj）=0.由命题3知crD（G16，Ti∪Tj）≥3.又因cr（K5，3）=4，故有crD（Ti∪Tj， Tk）≥4（对任意的k≠i，j），由命题1知，这与（2）式矛盾.

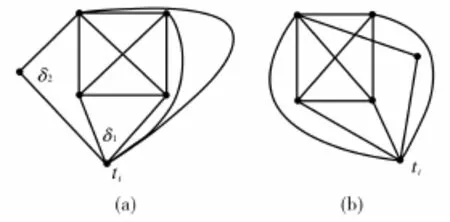
图4　图G16∪Ti满足crD（G16，Ti）=0的所有可能子画法Fig.4 The possible subdrawings of G16∪Tiwith crD（G16，Ti）=0

情形2：对任意的Ti，Tj（i，j∈｛1，2，…，n｝），满足crD（Ti，Tj）≥1.

1）若有i≠j，使得crD（Ti，Tj）=1，则由图3知crD（G16∪Ti，Tj）≥3.若crD（G16∪Ti，Tj）≥4，则由命题2知，这与（2）式矛盾.若crD（G16∪Ti，Tj）=3，则G16∪Ti∪Tj的所有可能画法如图5所示.

在图5中，运用计数方法可知，对任意的k≠i，j，当tk位于区域ω 之外时，为保证对任意的i≠j，有crD（Ti，Tj）≥1，可得crD（G16∪Ti∪Tj，Tk）≥6，则由图的交叉数的性质得，这与（2）式矛盾.

图5　当crD（Ti，Tj）=1，crD（G16∪Ti，Tj）=3时，图G16∪Ti∪Tj的所有可能画法Fig.5 The possible subdrawings of G16∪Ti∪Tjwith crD（Ti，Tj）=1 and crD（G16∪Ti，Tj）=3

当tk位于区域ω 时，有crD（G16∪Ti∪Tj，Tk）≥5，故只须讨论存在tk使得crD（G16∪Ti∪Tj，Tk）=5的情况.

当tk位于图5（a）中ω 区域时，当且仅当crD（G16，Tk）=0时crD（G16∪Ti∪Tj，Tk）=5才成立，故可得crD（Ti∪Tj，Tk）=5.又由图5（a）知，crD（Ti∪Tj，G16）=2，故由命题1知，这与（2）式矛盾.

当tk位于图5（b）（c）（d）中ω 区域时，在相应的图G16∪Ti∪Tj∪Tk中计数可得crD（G16∪Ti∪Tj∪Tk，Tl）≥7.若对任意的l≠i，j，k，有crD（G16∪Ti∪Tj∪Tk，Tl）≥8，则同上分析可得与（2）式矛盾.若存在l，使得crD（G16∪Ti∪Tj∪Tk，Tl）=7（当tk位于图5（b）和（c）中一个特定区域时会出现这种情况），则继续计数，可得对任意的m≠i，j，k，l，有crD（G16∪Ti∪Tj∪Tk∪Tl，Tm）≥10，同上分析可得与（2）式矛盾.

2）对任意的Ti，Tj（i，j∈｛1，2，…，n｝），满足crD（Ti，Tj）≥2.由假设知，对任意的k≠i，j，有crD（Ti∪Tj，Tk）≥4.若i≠j，使得crD（Ti，Tj）=2，则由图3知crD（G16，Ti∪Tj）≥1；若对任意的i≠j，有crD（Ti，Tj）≥3，则由命题1知，这2种情形下都有crD（G16+n K1）≥Z（5，n）+n+n/2，此与（2）式矛盾.定理1证毕.

2　联图G16+Pn的交叉数

在图G16+n K1中通过连接点t1，t2，…，tn构成路Pn可得图G16+Pn，故有

证明 由于图G16+n K1是G16+Pn的子图，故根据图的交叉数的性质［6］208和定理1，有

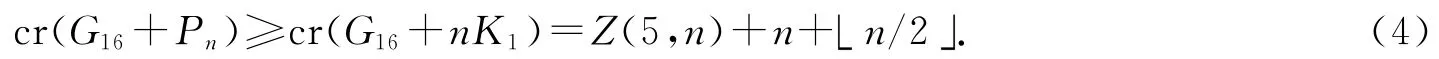
在图2中，连接点t1，t2，…，tn形成路Pn时可令其仅与G16的边cd 相交，即可得下面假设图G16+Pn有好画法D，使得

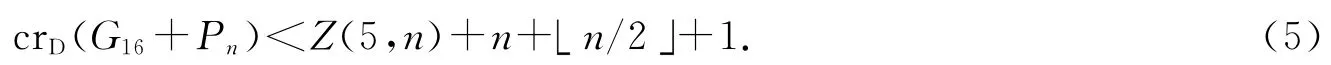
情形1：存在Ti（i∈｛1，2，…，n｝），使得crD（G16，Ti）=0.

若设crD（G16，Ti）=0，则G16∪Tn只有2种画法（如图4所示）.

1）当ti（i∈｛1，2，…，n-1｝）位于图4中除δ1，δ2外的任何含tn的区域时，因它最多只可能含G16的2个点且与它相邻的区域只含3个顶点在边界上，因此crD（G16∪Tn，Ti）≥4，于是，矛盾.

2）当ti（i∈｛1，2，…，n-1｝）位于δ1或δ2时，有crD（G16∪Tn，Ti）≥3，crD（G16）=1.若对任意的Ti（i∈｛1，2，…，n-1｝），有crD（G16∪Tn，Ti）≥4，则由情形1之1）知，矛盾.若存在Ti使得crD（G16∪Tn，Ti）=3，不妨设i=n-1，则可得crD（G16∪Tn-1∪Tn）≥4，crD（G16，Tn-1）=0.又因路Pn的边上无交叉点，故由图4（a）知crD（Tk，G16∪Tn-1∪Tn）≥7（k∈｛1，…，n-2｝）.同上分析可得，这与（5）式矛盾.

情形2：对任意Ti（i∈｛1，2，…，n｝），有crD（G16，Ti）≥1.

由cr（G16+2K1）=3知crD（G16∪Tn-1∪Tn）≥3.又因路Pn的边上无交叉点，故可得crD（Tk，G16∪Ti∪Tj）≥7，k≠i，j.由情形1之2）知，这与（5）式矛盾.定理2证毕.

3　联图G16+Cn的交叉数

图G16+Cn可以通过在图G16+n K1中连接点t1，t2，…，tn形成圈Cn而得到，故有由于5K1+Cn是图G16+Cn的子图，记Tx为G16的点x 与点t1，t2，…，tn相连而成的图，因此

证明 在图2中，当连接t1，t2，…，tn构成圈Cn时它可以仅与G16的边交叉3次，即得下证反向不等式.假设存在好画法D，使得，则由定理1，2知，Cn边上最多只有2个交叉点.

若crD（Cn）=0，则当crD（G16，Cn）=0且crD（Tx，Cn）=0（x∈｛a，…，e｝）时，G16+Cn在D下至少有个交叉点［4］166.当某个crD（Tx，Cn）≥1时，由crD（G16，Cn）=0得，此时G16+ Cn至少有个交叉点.当crD（G16，Cn）≥1时，由前述假设Cn边上最多只有2个交叉点得，边ce和Cn交叉，故G16+Cn至少有个交叉点.这些结论都与假设矛盾.

若crD（Cn）≠0，此时所有Tx（x∈｛a，…，e｝）在Cn的那个包含t1，t2，…，tn的区域内，则G16+Cn在D下至少有个交叉点，这与假设矛盾.证毕.

［1］GAREY M R，JOHNSON D S.Crossing number is NP-complete［J］.SIAM J Alg Discrete Meth，1983，4（3）：312-316.

［6］周志东，黄元秋，彭小多，等.一个小图与路和圈的联图的交叉数［J］.系统科学与数学，2013，33（2）：206-216.

［8］王晶，黄元秋.Sm∨Pn与Sm∨Cn的交叉数［J］.数学进展，2011，40（5）：631-636.

［9］黄元秋，王晶.图的交叉数综述［J］.华东师范大学学报：自然科学版，2010（3）：68-80.

［10］BONDY J A，MURTY U S R.Graph theory with applications［M］.London：Macmillan，1976：1-12.

The crossing numbers of the join of a 5-vertex graph with vertex，path and cycle

LI Min
（Sch of Math&Comput Sci，Hubei Univ of Arts&Sci，Xiangyang 441053，China）

This paper discusses the crossing numbers of the ioin of n K1，Pnand Cnwith a 5-vertex graph G16，i.e.，，，，n≥3，where n K1denotes n isolated vertices，while Pnand Cnare the path and cycle on n vertices，respectively.

5-vertex graph；crossing number；ioin；path；cycle

O 157.5

A 1007-824X（2015）01-0004-05

（责任编辑 秋 实）

2013-12-03.E-mail：fyi020512@126.com.

湖北省自然科学基金资助项目（2012FFC053）.

李敏.一个5阶图与点、路、圈联图的交叉数［ J］.扬州大学学报：自然科学版，2015，18（1）：4-8.