蒸汽凝结过程声压波动信号实验研究
2015-10-15唐继国阎昌琪孙立成李亚王开元
唐继国,阎昌琪,孙立成,李亚,王开元
蒸汽凝结过程声压波动信号实验研究
唐继国1,阎昌琪1,孙立成2,李亚1,王开元1
(1哈尔滨工程大学核安全与仿真技术国防重点学科实验室,黑龙江哈尔滨 150001;2四川大学水利水电学院,水力学与山区河流开发保护国家重点实验室,四川成都610207)
利用高速摄像仪和水声换能器研究蒸汽凝结时的声压波动信号和凝结区域的转变。结果表明,随过冷度和蒸汽流量升高分别出现3个不同的凝结区域——体积波动区、过渡区和毛细波区。此外,观察到两种分别对应气泡分裂和破碎的声压波动波形。声压波动信号的峰度存在阶跃变化,且阶跃处与凝结区域转变的阈值接近。幅度谱的低频区域存在频率在150~300 Hz的峰值,其可能是由蒸汽体积周期性变化引入。在过渡区和毛细波区发现频率高于7000 Hz的峰值,其可能是由气泡突然破碎引入的局部压力高频振荡造成的。蒸汽气泡破碎频率随过冷度和蒸汽流量增加而增加,且与幅度谱中首峰频率接近,误差在±20%以内。
凝结;气泡破裂;声压波动信号;气液两相流;传热
引 言
由于极高的传热和传质能力,直接接触凝结(direct contact condensation, DCC)现象在化工、核能和航空航天等诸多领域都有极其重要的应用,如汽水混合加热器、蒸汽喷射泵以及抑压式安全壳中用于降低壳内压力的抑压水池等。凝结状态和压力波动的研究对于应用直接接触凝结现象的装置和设备的优化设计以及安全运行等有着重要作用。
Ju等[1]利用全息干涉仪和高速摄像测量了凝结过程中气泡周围的传热系数。Youn等[2]研究了低蒸汽流速下的DCC现象。而Clerx等[3]和Xu等[4]则对流动条件下的DCC进行了研究。武心壮等[5]和Qiu等[6-7]分别分析了亚声速和声速下DCC过程中的压力特性。Cho等[8]研究了多孔蒸汽注射下的DCC现象,并分析了孔径和孔间距等对压力波动的影响。Takase等[9]通过数值分析的方法研究了抑压水池中蒸汽凝结的特性。Gulawani等[10]用CFX中的Thermal Ohase Change模型研究了亚声速和声速下的DCC现象。Chan等[11]、Lee等[12]、Elperin等[13]以及Petrovic[14]根据实验结果和理论分析提出了二维的DCC区谱图。而Petrovic等[15]随后以蒸汽质量流速、水温以及管径建立了三维的DCC分区谱图。Ueno等[16-17]利用过冷水中蒸汽的凝结过程模拟过冷沸腾时过冷液体与气泡间的相互作用,以此来简化对于一种特殊的沸腾现象,气泡微细化沸腾(microbubble emission boiling, MEB)形成机理的分析。
由于蒸汽气泡的生长、凝结、分裂以及破碎等行为,DCC过程中声信号的产生是不可避免的。尽管目前国内外学者对DCC进行了大量的研究,但是DCC发生时的声信号特性以及其应用却少有报道。水声换能器(水听器)由于其突出的水下信号检测能力而被广泛应用于多相流系统声信号的研究中[18-20]。因此,本文利用水声换能器采集不同工况下蒸汽气泡凝结时的声压波动信号,并对其进行时域和频域特性分析,以研究蒸汽凝结时的声压波动特性以及凝结区域转变。
1 实验装置
实验装置如图1所示。蒸汽由电加热锅炉产生,通过内径4 mm的孔板注入到水箱中。蒸汽流量通过蒸汽阀与旁通阀调节。水箱中的水温用直径0.5 mm的K型铠装热电偶测量,测点距蒸汽管道轴心约45 mm。铜制冷却盘管和电加热棒用于调节和维持水箱中的水温,水温波动被控制在±1 K内。水声换能器(RHS-20)用于采集声压波动信号,其与蒸汽出口竖直方向上的距离约5 mm,水平方向上的距离约50 mm。实验中水声换能器的采样频率为51.2 kHz,采样时间为1 s,每组工况采集4~6组数据。温度信号和声压波动信号由NI数据采集系统采集。蒸汽气泡凝结过程由PHOTRON公司生产的高速摄影仪(Fastcam SA5)记录。实验中采用背光系统以增强拍摄的清晰度。
2 蒸汽凝结过程可视化研究
10~70 K过冷度、0.74~3.73 m3·h-1蒸汽体积流量下,随过冷度和蒸汽流量增加分别出现3种不同的凝结区域:体积波动区(shape oscillation regime)、过渡区(transition regime)以及毛细波区(capillary wave regime)。不同过冷度、蒸汽流量下3个凝结区域分布如图2所示。图3示出这3个蒸汽凝结区域中典型的可视化结果。在体积波动区,随气泡生长,其局部开始出现较弱的界面波动,且缓慢发展,如图3(a)所示。随后,气泡脱离蒸汽管道,逐渐分裂成数个小气泡。在毛细波区,由于凝结作用强,气泡表面的波动会逐渐发展成毛细波,其波长与幅值均极小。当气泡脱离蒸汽管道后立即破碎成大量微小气泡,如图3(c)所示。过渡区可看作体积波动区和毛细波区的过渡。如图3(b)所示,过渡区气泡表面的波动强于体积波动区而弱于毛细波区。此外,气泡在脱离后不会立即破碎,而是逐渐凝结,在其凝结到一定程度后再破碎成许多微小汽泡。
过渡区和毛细波区中发生的气泡破碎现象会导致过冷水中出现较强的压力波动以及噪声。应用DCC现象的装置和设备因而会受到一定的冲击,其运行、寿命和隐蔽性等受到影响。然而,凝结状态一旦进入毛细波区,由于气泡表面的毛细波极大增加了有效凝结面积,蒸汽与过冷水间的传热和传质会有阶跃性的提升,这对利用直接接触凝结现象换热或混合的设备却极其有利。因此,蒸汽凝结时的声压波动的研究以及不同凝结状态的识别具有十分重要的意义。
3 蒸汽凝结时声压波动信号研究
3.1 时域分析
图4所示是3个凝结区域中典型的声压波动信号以及未通入蒸汽时的本底。未通入蒸汽时的声压波动信号为环境噪声,如图4(a)所示,此时的信号幅值均处于0 mV左右。这说明环境噪声对声压波动信号幅值的影响可以忽略。如图4(b)所示,在体积波动区,声压波动信号的幅值极小,这说明由气泡逐渐分裂而引入的声压波动较弱。如图4(c)和(d)所示,在过渡区和毛细波区,声压波动信号呈现高幅值的脉冲波动,这说明气泡破碎现象会引入剧烈的声压波动。
不同过冷度和蒸汽流量下信号中发现两种不同的波形,如图5所示。在体积波动区只观察到第1种波形;在毛细波区只观察到第2种;而在过渡区中的大部分信号包含第1种,少部分还可能包含第2种。此外,所观察到的第1种波形均以相对较大的负幅值开始,而第2种却以极高的正幅值开始。气泡突然破碎会产生具有极高能量的瞬时冲击,因此水声换能器检测到的第2种波形以较大幅值开始;由于瞬时冲击无法持续,能量逐渐以声能和热能的形式辐射而减少[21],因此第2种信号呈现衰减振荡的趋势。气泡逐渐分裂过程,无瞬时高能冲击产生,但是由于气泡分裂而迅速凝结消失,因此水声换能器检测到的第1种波形通常以相对较高的负幅值开始振荡。因此,第1种波形可能是由气泡分裂形成,而第2种则是由气泡破碎形成。
所采集的水声换能器声压波动信号的等间隔时间序列为(),其中=1, 2, ···,,为所采集信号的总样本。则信号的幅值最大值为
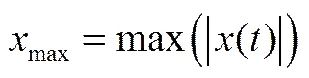
图6示出不同过冷度和蒸汽流量下声压波动信号的幅值最大值。如图所示,声压波动信号幅值最大值通常随过冷度和蒸汽流量的升高而增加,说明过冷度和蒸汽流量升高会加剧蒸汽气泡的破碎过程。而在3.73 m3·h-1蒸汽流量、60 K过冷度下,极强的蒸汽凝结作用可能使气泡未完全生长就破碎,因此该条件下最大幅值低于Qin=3.73 m3·h-1,DTsub=50 K和Qin=1.55 m3·h-1,DTsub=60 K时的最大幅值。
声压波动信号的标准偏差以及平均绝对偏差通常可以用来反映数据偏离平均值的程度,因此两者可以用来表征声压波动信号的整体波动强度。相比于标准偏差,平均绝对偏差可以更好地减小异常值的影响。两者可表示为

(3)

过冷度和蒸汽流量对声压波动信号标准偏差及平均绝对偏差的影响如图7所示。从图中可以看出,两者的变化趋势基本相同,Qin=0.74 m3·h-1时随过冷度升高而升高,而Qin=1.55和3.73 m3·h-1时随过冷度先增加后减小。这是由于在高过冷度、较高蒸汽流量下,凝结作用较强,会出现气泡未完全生长就破碎的情况。因此,所采集到的信号中会存在较多幅值较小的脉冲,信号的标准偏差和平均绝对偏差下降。
声压波动信号的最大幅值、标准偏差和平均绝对偏差显然无法明确判别凝结状态。因此,对信号的高阶矩进行分析。相比于信号的均值和偏差等,偏度和峰度对信号中的变化更加敏感,可表示为
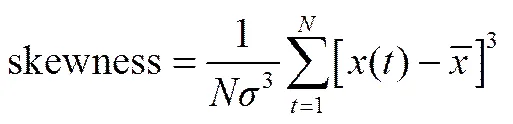
(6)
其中,偏度用于衡量信号概率分布的对称性,而峰度用于衡量信号概率分布的陡峭程度。图8和图9分别示出偏度和峰度随过冷度和蒸汽流量的变化。与Vial等[18]的实验结果一致,声压波动信号的偏度基本没有规律。如图9所示,不同蒸汽流量下声压波动信号的峰度随过冷度升高存在阶跃升高或下降,且阶跃处对应的过冷度与图2所示蒸汽凝结区域转变的过冷度基本一致。因此,通过信号的峰度可作为凝结区域转变的判据,而信号的幅值最大值、标准偏差、平均绝对偏差和偏度却不可以。
3.2 频域分析及气泡破碎频率
对图4所示的声压波动信号进行快速傅里叶变换(FFT),结果如图10所示。不同凝结区域的低频部分均发现频率在150~300 Hz的峰值,其频段范围与Qiu等[7]实验中主频的频段范围一致。Qiu等[7]认为低频区域的主频是由蒸汽体积周期性变化引入的。在过渡区和毛细波区的高频部分发现数个频率高于7000 Hz的峰值;而在体积波动区却未发现。此外,毛细波区的高频峰值的幅值通常高于过渡区;而各个区的低频峰值的幅值接近。如前所述,在过渡区和毛细波区,气泡会突然破碎并引入高能冲击,冲击在水中传播,并造成水声换能器附近局部压力高频振荡。这一高频振荡可能就是产生高频峰值的原因。
图10 不同凝结区域典型信号幅度谱
Fig. 10 Amplitude spectra of typical acoustic signals in different condensation regimes
信号幅度谱中的首峰频率通常代表周期最长的一种周期现象,可能与气泡周期性分裂或破碎行为有关。如图10所示,首峰频率通常在150 Hz以下,其随过冷度和蒸汽流量变化如图11所示。随过冷度和蒸汽流量增加,首峰频率增加。泡破碎频率根据可视化结果计算,其定义为连续两次气泡发生破碎或分裂时间间隔平均值的倒数,即

不同过冷度下气泡破碎频率如图12所示。由于过冷度和蒸汽流量的增加会分别减少气泡破碎前的凝结时间和生长时间,因此气泡破碎频率随过冷度和蒸汽流量升高而增加。对比图11和图12发现,两种频率所处频段以及变化规律接近,因此推测气泡分裂或破碎频率近似等于幅度谱中首峰频率,即
1=b(8)
两种频率比较示于图13。如图所示,幅度谱中首峰频率可以较好地间接测量气泡破碎频率,其误差在±20%以内。
综上所述,利用气泡凝结时的声压波动信号可以很好地识别出凝结所处的区域,并可对气泡破碎频率进行间接测量。这些均可为工程上应用DCC的装置的设计提供技术支持及检测方法。此外,气泡微细化沸腾作为一种具有极高换热能力的沸腾现象,其发生时会伴随气泡破碎现象,而且其发生时的热通量与气泡破碎频率有关。因此,本文的研究可为判别气泡微细化沸腾是否发生与间接测量其热通量提供了一种可行的方法。
4 结 论
本文利用高速摄像仪及水声换能器对10~70 K过冷度、0.74~3.73 m3·h-1蒸汽体积流量下的蒸汽凝结过程进行实验研究,得到如下结论。
(1)随过冷度和蒸汽流量升高分别发现3个凝结区域:体积波动区(shape oscillation regime)、过渡区(transition regime)和毛细波区(capillary wave regime)。在不同凝结区域的信号中发现两种分别对应气泡分裂和气泡破碎的波形。
(2)不同蒸汽流量下,声压波动信号的峰度随过冷度增加出现阶跃升高或下降,阶跃处的过冷度与凝结区域转变的过冷度基本一致。因此,信号的峰度可以用来判别凝结状态的转变,而幅值最大值、标准偏差、平均绝对偏差和偏度却不可以。
(3)频域分析发现,在低频部分,所有凝结区域的声压波动信号均存在峰值;而在高频部分,仅过渡区和毛细波区存在。低频峰值可能由蒸汽体积周期性波动造成,而高频峰值可能由气泡突然破碎引入的局部压力高频振荡造成。
(4)蒸汽气泡破碎频率随过冷度和蒸汽注射流量增加而增加,且与幅度谱中首峰频率接近,误差在±20%以内。
符 号 说 明

Aad——平均绝对偏差,mV f——频率,Hz fb——气泡破碎频率,Hz f1——首峰频率,Hz m——气泡破碎或分裂次数 N——采样频率 Qin——蒸汽体积流量,m3·h-1 DTsub——过冷度,K Dtj——连续两次气泡破碎或分裂的时间间隔,s xmax——幅值最大值,mV x(t)——水声换能器所采声压波动信号,mV ——平均值,mV s——标准偏差,mV
References
[1] Ju S H, No H C, Mayinger F. Measurement of heat transfer coefficients for direct contact condensation in core makeup tanks using holographic interferometer [J]., 2000, 199: 75-83.
[2] Youn D H, Ko K B, Lee Y Y, Kim M H, Bae Y Y, Park J K. The direct contact condensation of steam in a pool at low mass flux [J]., 2003, 40(10): 881-885.
[3] Clerx N, van der Geld C W M. Experimental and analytical study of intermittency in direct contact condensation of steam in cross-flow of water// ECI International Conference on Boiling Heat Transfer [C]. Florianopolis, Brazil, 2009.
[4] Xu Q, Guo L J, Zou S F, Chen J W, Zhang X M. Experimental study on direct contact condensation of stable steam jet in water flow in a vertical pipe [J]., 2013, 66: 808-817.
[5] Wu Xinzhuang (武心壮), Li Wenjun (李文军), Yan Junjie (严俊杰). Research on axial total pressure distributions of sonic steam jet in subcooled water [J].(核动力工程), 2012, 33(6): 76-80.
[6] Qiu B B, Tang S, Yan J J, Liu J P, Chong D T, Wu X Z. Experimental investigation on pressure oscillations caused by direct contact condensation of sonic steam jet [J]., 2014, 52: 270-277.
[7] Qiu B B, Yan J J, Liu J P, Chong D T, Zhao Q B, Wu X Z. Experimental investigation on the second dominant frequency of pressure oscillation for sonic steam jet in subcooled water [J].., 2014, 58: 131-138.
[8] Cho S, Chun S Y, Baek W P, Kim Y. Effect of multiple holes on the performance of sparger during direct contact condensation of steam [J]., 2004, 28: 629-638.
[9] Takase K, Ose Y, Kunugi T. Numerical study on direct-contact condensation of vapor in cold water [J]., 2002, 63/64: 421-428.
[10] Gulawani S S, Joshi J B, Shah M S, RamaPrasad CS, Shukla D S. CFD analysis of flow pattern and heat transfer in direct contact steam condensation [J].., 2006, 61: 5204-5220.
[11] Chan C K, Lee C K B. A regime map for direct contact condensation [J]., 1982, 8(1): 11-20.
[12] Lee S I, No H C. Gravity-driven injection experiments and direct-contact condensation regime map for passive high-pressure injection system [J]., 1998, 183: 213-234.
[13] Elperin T, Fominykh A. Map of regimes of pressure oscillations induced by absorption during gas jet injection through a submerged nozzle [J]., 1997, 32: 277-283.
[14] Petrovic A. Analytical study of flow regimes for direct contact condensation based on parametrical investigation [J].., 2005, 127: 20-25.
[15] Petrovic A, Calay R K, With G. Three-dimensional condensation regime diagram for direct contact condensation of steam injected into water [J]., 2007, 50(9/10): 1762-1770.
[16] Ueno I, Arima M. Behavior of vapor bubble in subcooled pool [J]., 2007, 19(3/4): 128-129.
[17] Ueno I, Hattori Y, Hosoya R. Condensation and collapse of vapor bubbles injected in subcooled pool [J]., 2011, 23: 73-77.
[18] Vial C, Camarasa E, Poncin S, Wild G, Midoux N, Bouillard J. Study of hydrodynamic behaviour of bubble columns and external loop airlift reactors through analysis of pressure fluctuations [J].., 2000, 55: 2957-2973.
[19] Ajbar A, Al-Masry W A, Ali E M. Prediction of flow regimes transitions in bubble columns using passive acoustic measurements [J].:, 2009, 48: 101-110.
[20] Zhang Qing(张擎), Dong Kezeng(董克增), Huang Zhengliang(黄正梁), Wang Jingdai(王靖岱), Yang Yongrong(阳永荣). Mode identification of pool boiling of water by acoustic emission [J].(化工学报), 2013, 64(10): 3527-3533.
[21] Leighton T G., Walton A J. An experimental study of the sound emitted from gas bubbles in a liquid [J].., 1987, 8: 98-104.
Condensation of vapor using sound pressure oscillation signals
TANG Jiguo1,YAN Changqi1,SUN Licheng2,LI Ya1,WANG Kaiyuan1
(1Fundamental Science on Nuclear Safety and Simulation Technology Laboratory, Harbin Engineering University, Harbin 150001, Heilongjiang, China;2State Key Laboratory of Hydraulics and Mountain River Engineering, College of Hydraulic and Hydra-electric Engineering, Sichuan University, Chengdu 610207, Sichuan, China)
Signals of sound pressure oscillations during vapor condensation and transition of condensation regimes were investigated using a high-speed video camera and a hydrophone. Results indicate three different condensation regimes with the increase of subcooling and vapor injection rates, which are referred to as bubble oscillation regime, transition regime and capillary wave regime. In addition, two waveforms occur in the detected signals, of which sources are vapor bubble split-up and collapse. The kurtosis of the signals presents step changes, which is close to the transformation threshold of condensation regimes. The peak at frequency of 150—300 Hz appears in spectra in all condensation regimes, which may be resulted from the periodic variation in vapor volume. The peaks with frequency higher than 7000 Hz appear only in transition and capillary wave regimes and may be the resultant of the high-frequency oscillation in pressure caused by sudden collapse of vapor bubbles. The bubble collapse frequency increases with the increase of subcooling and vapor injection rates and is close to the frequency of the first peak in spectra with an error within ±20%.
condensation; bubble collapse; sound pressure oscillation signal; gas-liquid flow; heat transfer
2015-01-20.
supported by the National Natural Science Foundation of China (51376052, 11475048, 51106101) and the Scientific Research Foundation of Sichuan University (YJ201432).
Prof. YAN Changqi, changqi_yan@163.com
10.11949/j.issn.0438-1157.20150080
TK 124
A
0438—1157(2015)07—2442—08
国家自然科学基金项目(51376052,11475048,51106101);四川大学科研基金项目(YJ201432)。
2015-01-20收到初稿,2015-02-27收到修改稿。
联系人:阎昌琪。第一作者:唐继国(1988—),男,博士研究生。
