源于生活 用于生活——数学活动课《图形的密铺》活动设计
2015-10-15江苏省盐城市郭猛实验学校胡安中
江苏省盐城市郭猛实验学校 胡安中
数学知识来源于生活,数学教学实际上与学生活动有着密不可分的联系。新课程强调:有效的数学活动不能单纯地依赖模仿与记忆,动手实践、自主探索与合作交流是学生学习的重要形式。
苏科版初中数学教材在每章结束后,都统一安排了“数学活动”这一栏目。数学活动课,是指以在教学过程中构建具有教育性、创造性、实践性的学生主题活动为主要形式,以激励学生主动参与、主动实践、主动思考、主动探索、主动创造为基本特征,以促进学生整体素质全面提高为目的的一种新型的教学观和教学形式。数学活动课属于活动课程,活动课程是与学科课程相对应的一种学校课程形式,是在教师指导下,通过学生的主动活动,以获得直接经验和实践特长为主的课程。数学活动课的“活动”是一种启发、一种诱导,目的是通过“活动”激发学生的数学体验,最终要转化为思维活动,思维价值是数学活动课最为重要的一个方面。下面就苏科版九年级上册《图形的密铺》设计了这样几组活动:
活动一:
1.图片展示。
展示学生课外收集的用平面图形铺满地面的各种图案,让学生深切地感受数学美与现实生活的紧密联系。
2.交流讨论。
学生直观感受数学美的同时,引导学生思考:这些图案都是由哪些基本的平面图形构成的?学生细心观察之后发现,图案中的平面图形有的规则,有的不规则;有的用一种多边形拼成,有的用多种多边形拼成,培养学生分类的思想。
3.感知概念。
讨论这些图形拼成一个平面的共同特征,注意到各图形之间没有空隙,也没有重叠。在充分交流的基础上,用自己的语言概括图形的密铺概念。教师给予鼓励和评价,再给出图形的密铺定义。
4.提出问题。
让学生都来当设计师。提问:如果让你们设计几种地板图案,需要解决什么问题?学生自主探索,分组研究需要探讨的问题,教师适当引导。把其中可能列举的典型问题设想如下:(1)怎样铺设可以不留空隙,也不相互重叠?(2)可以用哪些图形?(3)用前面所学的正多边形能否拼成一个平面图形?(4)哪些正多边形可以密铺成一个平面,哪些不能?根据学生提出的以及本节课需要解决的问题,首先引导学生研究最简单的密铺问题。
活动二:
探索:只用一种正多边形密铺,正几边形可以密铺成一个平面。
1.动手实验。
把全班同学分成几个小组,拿出课前准备好的正三角形、正四边形、正五边形、正六边形,以小组为单位进行比赛,看哪个小组拼得又快又好。并派代表在投影仪上展示他们的成果。
2.收集数据。
根据刚才的动手实验,引导学生收集数据,观察结果。
3.分析数据。
引导学生分析收集的数据,寻找其中的规律。
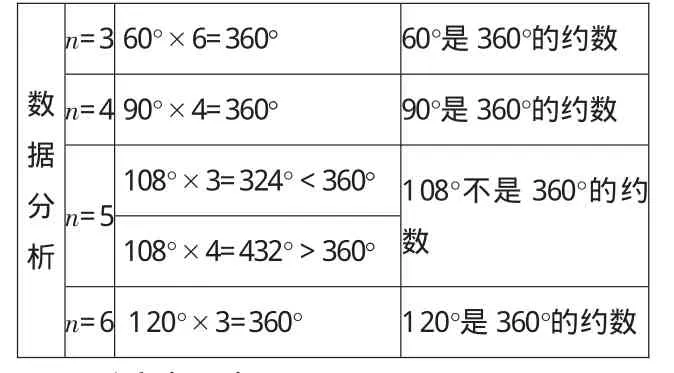
数据分析n=3 60°×6=360° 60°是 360°的约数n=4 90°×4=360° 90°是 360°的约数108°×3=324°<360° 108°不是 360°的约数108°×4=432°>360°n=6 120°×3=360° 120°是 360°的约数n=5
4.活动思考。
通过动手操作,让学生思考为什么有的正多边形能进行密铺,而有的正多边形不能?对于正十边形、正二十边形、正一百边形它们能否密铺呢?那么,用一种正多边形密铺需要满足什么条件呢?
5.得出结论。
学生根据自己实验的结果,积极思考,不难得出结论:
(1)正三角形、正四边形、正六边形能够密铺,正五边形不能密铺。
(2)当围绕一点拼在一起的几个正多边形的内角加在一起恰好组成一个周角时,就拼成一个平面图形。要用一种正多边形密铺,那么这个正多边形的每个内角度数能整除360°。
活动三:
1.质疑。
用两种正多边形进行密铺。思考:用两种正多边形密铺需满足什么条件?
2.猜想。
对于正三角形、正四边形、正五边形、正六边形,哪两种正多边形能进行密铺?学生通过画图、列式等途径进行猜测,然后请学生各自发表意见,列举方案。
3.验证。
根据学生的不同方案,动手实践,验证观点是否正确。
学生拿出课前准备好的这些正多边形,仍然以小组为单位进行拼图,看哪些能用来搭配密铺成一个平面。
4.引申。
用三种或多种正多边形能否进行密铺,若能,又需满足什么条件?
活动四:
应用并设计正多边形密铺的图案。首先设计一道与生活有关但又要充分运用密铺知识的问题,让“数学源于生活,用于生活”这一理念贯串始终。然后让学生根据所学知识设计出各种各样的密铺图案,肯定学生的各种设计并展示优秀作品。
这是一节数学活动课。依照课程标准的要求,结合本节课的具体内容,将其设计成四个活动。在活动的设计中,注重从学生已有的生活经验和数学经验出发,为学生创设丰富的亲身经历、体验知识发生、发展过程、获取数学知识的活动情境。
本节课的内容与生活密切相关,活动一首先让学生从身边的事物中寻找与图形的密铺有关图案,初步形成对密铺的直观感知。这种生活化的设计使学生明白数学来源于生活,同时也能感受到数学的美,从而产生强烈的探究欲望并积极投入探究活动之中。活动二设计了“动手实验、收集数据、分析数据、实验思考、得出结论”五个教学环节,让学生充分体验数学认知的全过程。学生将通过动手实验、分析实验结果等过程掌握用一种正多边形进行密铺的规律;在活动二的理解基础上设计活动三,通过“质疑、猜想、验证、引申”等环节将学生对镶嵌的理解由感性认识提高到理性认识,把学生的思维领向一个更深的层次。通过以上活动,学生已经掌握了镶嵌的一般规律。在活动四中,让学生在实际生活中应用所学知识并动手设计镶嵌图案,既巩固了所学知识,又能感受到数学创造的乐趣。
伴随着CAI技术的日新月异,数学活动的教学内容将逐渐增加,活动素材库将不断壮大,活动技术将更为先进与精巧,因而数学活动的教学思想和模式将具有更为广阔的天地和更为重大的作为。
