无方位模糊的非均匀稀疏阵MVDR测向方法

李倩茹，宋志杰，王良，杨晴



无方位模糊的非均匀稀疏阵MVDR测向方法

李倩茹，宋志杰，王良，杨晴

(中国海洋大学信息科学与工程学院，山东青岛266100)

稀疏阵能够获得更大的阵列孔径，但常规波束形成(Conventional Beam-Forming, CBF)对非均匀稀疏阵测向时会出现方位模糊。提出了一种基于最小方差无畸变响应(Minimal Variance Distortionless Response, MVDR)同局部非稀疏的非均匀稀疏阵(Non-Uniform Sparse Array, NUSA)的设计相结合来抑制方位模糊的方法(NUSA+MVDR)，对其无方位模糊现象进行了理论分析，表明MVDR这一非线性处理方法对伪峰有很好的抑制能力。针对一种典型的NUSA(Typical NUSA, TNUSA)，进行了TNUSA+MVDR数值仿真实验，其结果和理论分析一致，表明：① MVDR有很强的NUSA检测能力，在所给仿真条件下，等效阵元间距为50倍波长时，仍能很好地抑制方位模糊；②TNUSA+MVDR较阵元数相同的均匀非稀疏阵列的CBF和MVDR有更高的方位分辨力；③阵元数一定，TNUSA+MVDR方位分辨力随着等效间距增加而提高，最小可分辨角度反比于等效间距；④等效间距一定，TNUSA+MVDR方位分辨力随阵元数增加而增加。海上实验在等效阵元间距为10倍波长条件下部分验证了NUSA+MVDR的检测性能。

非均匀稀疏阵；最小方差无畸变响应；被动测向

0 引言

在阵列处理技术中，阵列几何结构是决定其空域滤波性能的重要因素[1]，多数测向方法都是在均匀阵的基础上提出的[2]。为满足空间采样定理[3]，阵元间距须小于等于信号波长的一半，阵列孔径和分辨能力受到限制。非均匀稀疏阵打破了空间采样定理的限制，通过对阵元的合理配置可以以较少的阵元获得较大的孔径并且不出现栅瓣，从而使得阵列波束变窄而空间分辨力更高。在卫星接收、地面雷达、射电天文和声呐探测等领域，非均匀稀疏阵都有广泛的应用前景[2,4,5]，但非均匀稀疏阵也会不同程度地出现方位估计模糊的问题[6]。

在基于CBF和子空间算法的线性检测背景下，文献[7,8]分析了非均匀阵列产生信号模糊的原因，提出当各阵元间距组成的各数间两两互质时，整个线阵方位估计无模糊，并根据这一原理设计了最小冗余阵列、中心对称阵列等非均匀阵列，利用阵列几何设置以尽可能避免伪峰的产生。但最小冗余阵列在给定阵长条件下对阵元数要求苛刻，对阵列信噪比处理增益的提高有一定局限性。在非线性检测背景下，利用宽带信号中不同频率栅瓣出现的位置不同[9]，文献[10,11]分别提出了利用宽带MVDR抑制均匀稀疏阵的方位估计模糊问题，并通过数值仿真和实验数据处理验证其效果，而对窄带信号则仍存在方位估计模糊问题。实际上，非均匀稀疏阵测向属于空间压缩感知问题，但由于空间压缩感知理论基于特征子空间的提取，因此在低信噪比条件下有一定的局限性[12,13]。

本文提出一种NUSA阵列结构和MVDR相结合的稀疏阵被动信号检测(NUSA+MVDR)方法，预期该方法对方位估计模糊问题有很好的抑制能力。先就NUSA+MVDR对方位估计模糊问题的抑制能力进行理论分析；然后，就一种典型的TNUSA阵列进行TNUSA+MVDR方法的数值仿真研究，并通过海上实验数据处理部分验证了理论分析和仿真结果；最后给出结论。

1 NUSA+MVDR方法

NUSA是指阵列局部满足空间采样定理(非稀疏)而整体不满足空间采样定理(稀疏)的一种非均匀稀疏阵列结构。NUSA+MVDR是在NUSA阵列结构下利用最小方差无畸变响应自适应波束形成来实现被动测向的一种方法。

为简洁计，下面以一维线阵为例进行讨论。阵列结构如图1所示，，其中为阵元数，为阵元标号，参考阵元位于坐标原点，为第个阵元的坐标，为相邻阵元间距，为阵列长度。当至少存在一个，满足大于半波长时，称相应阵列为稀疏阵列。在稀疏阵列中，若至少存在一个(且)，称该稀疏阵列为非均匀稀疏阵列(Non-Equal Sparse Array, NESA)。当NESA满足至少存在一个()时，称该NESA为局部非稀疏的非均匀稀疏阵(Non-Uniform Sparse Array, NUSA)。为方便和均匀稀疏阵对比，定义NUSA的等效阵元间距为。

对简谐平面波，阵列的导向矢量为

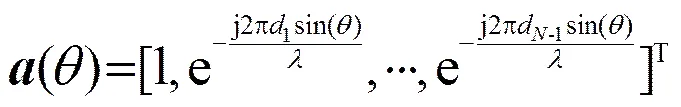
其中，θ为入射平面波与阵列法线方向的夹角，λ为入射平面波波长。

1.1 伪峰和栅瓣

文献中一般不区分伪峰和栅瓣。本文的讨论需要区分两者，认为方位估计模糊问题是由伪峰和栅瓣两种起因构成。栅瓣具有和主瓣相同的导向矢量，其波束响应峰值和主峰相同。NUSA在局部满足空间采样定理时，因此整个阵列不存在完全相同的两个导向矢量，即不存在栅瓣。伪峰指波束响应低于主瓣，但明显高于旁瓣的那些极值点。

CBF利用阵列提取平面波幅值或功率信息的过程是：经导向矢量匹配后，期望信号在各阵元上的响应具有相同幅值和相位，即所谓空间直流分布，再利用加法器作为低通滤波器提取空间直流成分。而伪峰所指方向，虽没有真实目标，但导向矢量匹配后可能存在虚假直流成分，加法器的低通滤波不能有效对其抑制，从而形成伪峰。如图2所示，12阵元的NUSA，前4个阵元间距为，后8个阵元间距为，目标在0°方向，图2(a)为CBF方位响应图；图2(b)和图2(c)分别为真实信号和伪峰方向匹配后各阵元的相位分布图。

图2(a)表明，除在0°方向存在峰值外，在±42°附近分别有两个伪峰，且两个伪峰的峰值低于真实信号方向的峰值。图2(b)表明，匹配后，真实信号方向各阵元上的相位分布相同，为真实的直流分布。从图2(c)可以看出，在42°的伪峰方向，前四个阵元相位分布不同，后八个阵元的相位分布基本一致，在整个阵列上形成了虚假的直流成分，CBF利用加法器作为低通滤波不能有效抑制虚假直流成分导致了伪峰的产生。由于NUSA不存在栅瓣，下面主要讨论伪峰的抑制问题。

1.2 NUSA+MVDR方法

如图1所示，平面波入射到NUSA阵列上，阵元输出为

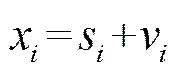
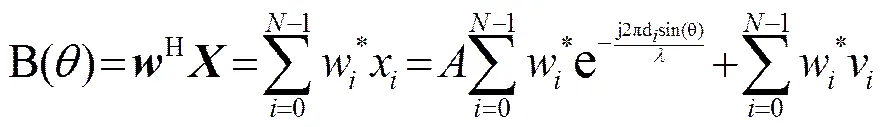
其中，*表示共轭，H表示转置共轭。

为保障期望的空间直流信号全部通过，要求滤波器满足条件

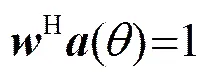
在满足式(4)的条件下，波束输出功率为

(5)

在保障期望的空间直流信号全部通过的条件下，使输出信噪比最大即噪声功率最小，MVDR问题可表述为如下有约束的优化估计问题

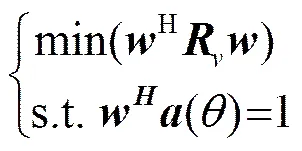
注意到式(5)波束输出功率中期望信号为常数，假设噪声与信号不相关，则式(6)的优化估计问题等价为

(7)

由拉格朗日乘数法可得式(7)的优化解为

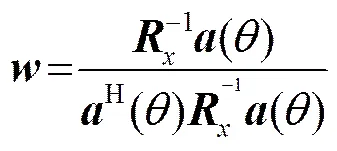
优化波束输出功率为

(9)

将式(8)代入到式(3)中，MVDR优化权向量先将期望信号匹配为空间直流，再通过约束条件式(4)将其保护起来，进一步调节权向量使噪声输出功率最小而获得最大信噪比输出。由1.1节可知，伪峰对应的阵列上的信号分布并不是真正的空间直流分布，即是不受约束条件保护的成分，MVDR滤波器将通过调节各个阵元上的权来压低这部分虚假空间直流对输出的贡献。因此，波束输出功率中伪峰的成分必将受到MVDR滤波器的抑制而减少。由于不产生栅瓣且有很好的伪峰抑制能力，可以预期，即便是对于简谐平面波(窄带信号)，NUSA+ MVDR对伪峰引起的方位模糊现象也会有很好的抑制效果，并且由于更宽的孔径而有更高的方位分辨力。

2 一种典型的NUSA+MVDR及其数值仿真研究

本文研究一种典型的NUSA(Typical NUSA, TNUSA)，该阵列由两个相同标准子阵组成，如图1所示，每个子阵由个阵元组成，子阵中阵元间距，而两子阵间距远大于，整个阵列满足NUSA条件。本节通过数值仿真研究TNUSA+ MVDR的方位估计性能。仿真条件为：声源为满足平面波条件的CW脉冲信号。选取的信号频率为500 Hz，信号波长为3 m，信号长度为1 s，采样率为8 kHz，信噪比为20 dB，信号由30°方向入射。

2.1 和CBF的方位估计性能对比

选取由两个8阵元标准子阵组成的16阵元TNUSA，等效阵元间距，真实信源位于30°方向，阵元输入信噪比为20 dB，分别用CBF和MVDR波束形成对该阵型的方位估计性能进行计算机仿真，结果如图3所示。

图3中，CBF和MVDR方位响应均无栅瓣出现，但是在CBF方位响应中存在多个伪峰，而MVDR方位响应中只有比主瓣低35 dB的旁瓣。可见，NUSA+MVDR确能抑制伪峰，不发生方位模糊现象。

2.2 等效阵元间距的影响

2.3 阵元数对方位模糊抑制能力的影响

分析阵元数对TNUSA+MVDR方位模糊抑制能力的影响，在的条件下，分别选取阵元数为16、32、64进行TNUSA+MVDR仿真，结果如图5所示。从图5可以看出，随着阵列阵元数的增加，主瓣逐渐变窄且旁瓣逐渐变低。这个现象是由于MVDR阵列权矢量的自由度随阵元数的增加而增加，抑制非期望方向干扰的能力增加，使得主瓣宽度变窄，从而提高了抑制方位模糊的能力。

2.4 TNUSA+MVDR的方位分辨力

大量的仿真研究表明，TNUSA+MVDR的方位分辨力，不仅受到由稀疏引起的阵列孔径的增加的影响，还会受到组成阵列的阵元数的影响。此处给出在不同阵元数条件下，最小可分辨角度随等效阵元间距变化的仿真结果。

由图4和图5可知，阵元数和等效阵元间距都影响TNUSA+MVDR的波束性能。因此，这两个因素将共同影响着TNUSA+MVDR的方位分辨能力。这里以阵元数为参量，仿真研究TNUSA+MVDR对两个等强度信源的最小可分辨角度(刚刚能分辨两信源方向时两信源的间隔角度)随等效阵元间距的变化规律。

在阵元数分别为32、48和64时，图6给出了TNUSA+MVDR最小可分辨角度随等效阵元间距的变化。从图6中可以看出，(1) 阵元数一定时，TNUSA+MVDR最小可分辨角度随等效阵元间距的增加而减小，近似成反比例关系；(2) 等效阵元间距一定时，TNUSA+MVDR最小可分辨角度随阵元数的增加而减小。以上结果对TNUSA+MVDR阵列的设计具有重要的参考价值。

3 海上实验数据处理

利用海上水声实验数据可以部分地验证理论分析和仿真结果。实验中采用的TNUSA由两个相同子阵组成，每个子阵由10个阵元的水平线阵组成，子阵阵元间距，两子阵间距为，等效阵元间距，满足平面波条件的CW声脉冲信号源位于-11º，发射脉冲信号长度为0.1 s，脉冲重复周期为20 s，信号采样率为96 kHz。实验结果如图7和图8所示。

图7(a)、7(b)分别为TNUSA的CBF和MVDR处理海试数据所得方位历程图。可以看出，MVDR波束形成较常规波束形成波束宽度明显变窄，这是由于MVDR波束形成对常规波束形成信号方位附近的较高的旁瓣有显著的抑制作用。图8(a)、8(b)分别为1700 s时CBF和MVDR的方位响应图。比较TNUSA+MVDR和TNUSA+CBF可知，前者不存在方位模糊现象且旁瓣很低，而后者明显存在方位模糊现象。

4 结论

本文针对稀疏阵方位估计模糊的问题，提出了NUSA+MVDR方法，对其无方位模糊现象进行了理论分析，并对一种典型的TNUSA进行了TNUSA+MVDR数值仿真研究，结果表明：①在本文所给仿真条件下，等效阵元间距为50倍波长时，TNUSA+MVDR仍能实现无方位模糊的方位估计，表明了MVDR这种非线性处理方法应用于非均匀稀疏阵的强大抑制方位模糊能力；②TNUSA+ MVDR较阵元数相同的均匀非稀疏阵列的CBF和MVDR有更高的方位分辨力；③阵元数一定，TNUSA+MVDR方位分辨力随着等效间距增加而增加，最小可分辨角度反比于等效间距；④等效间距一定时，TNUSA+MVDR方位分辨力随阵元数的增加而增加。海上实验在等效阵元间距为10倍波长条件下部分验证了NUSA+MVDR的检测性能。利用海上实验数据处理，验证了NUSA+MVDR方法的有效性，部分验证了理论分析和仿真研究的结果。

本文只给出了部分NUSA+MVDR性能的实验验证，其在不同信噪比条件下的方位检测和分辨性能，还有待于进一步的实验验证。

[1] Harry L. Van Trees. Optimum array processing: PartⅣ of detection, estimation, and modulation theory[M]. New York: Wiley-Interscience, 2002.

[2] 孙秋生. 基于特定非均匀线阵的测向算法设计与实现[D]. 长沙: 国防科学技术大学, 2008.

SUN Qiusheng. The Design and Realization of Direction Finding Based On Specific Non-uniform Linear Array[D]. Changsha: National University of Defense Technology, 2008.

[3] 牟建明. 基于非均匀线阵的空间谱估计测向算法研究[D]. 南京: 南京理工大学, 2005.

MOU Jianming. Direction finding method of spatial spectrum estimation based on NULA[D]. Nanjing: Nanjing University of Science and Technology, 2005.

[4] 潘敏. 线形阵列栅瓣的抑制[J]. 大众科技, 2009, 11(12): 32-33.

PAN Min. Grating lobes suppression of linear array[J]. Popular Science & Technology, 2009, 11(12): 32-33.

[5] 李绍滨, 赵淑清, 宿富林. 非均匀天线阵的超分辨测向[J]. 哈尔滨工业大学学报, 2001, 33(6): 834-837.

LI Shaobing, ZHAO Shuqing, SU Fulin. Direction of arrival estimation on non-uniformly spaced arrays[J]. Journal of Harbin Institute of Technology, 2001, 33(6): 834-837.

[6] 闫禄, 解明祥, 柳宝鹏. 非均匀阵列模糊问题及测向性能分析[J]. 舰船电子工程, 2010, 30(2): 50-52.

YAN Lu, XIE Mingxiang, LIU Baopeng. Ambiguity and direction finding performance for non-uniformly spaced linear arrays[J]. Ship Electronic Engineering, 2010, 30(2): 50-52.

[7] 陈辉, 王永良, 万山虎. 利用阵列几何设置改善方位估计[J]. 电子学报, 1999, 27(9): 97-99.

CHEN Hui, WANG Yongliang, WAN Shanhu. Performance improvement in estimating direction-of arrival by array geometry arrangement[J]. Chinese Journal of Electronics, 1999, 27(9): 97-99.

[8] 王永良, 陈辉, 彭应宁. 空间谱估计理论与算法[M]. 北京: 清华大学出版社, 2004.

WANG Yongliang, CHEN Hui, PENG Yingning. Spatial spectrum estimation and algorithms[M]. Beijing: Tsinghua University Press, 2004.

[9] 吴国清, 王美刚. 无源声呐稀疏阵无栅瓣性能分析[J]. 声学学报, 2006, 31(6): 506-510.

WU Guoqing, WANG Meigang. Beam pattern of sparse array for passive sonar[J]. Acta Acustica, 2006, 31(6): 506-510.

[10] 杜鹏, 蒋行海,刘彦森. 基于宽带MVDR波束形成的稀疏阵被动测向方法[J]. 中国科技信息, 2010, 22(24): 103-111.

DU Peng, JIANG Xinghai, LIU Yansen. A thinned array passive direction finding method based on wideband MVDR beamforming[J]. China Science and Technology Information, 2010, 22(24): 103-111.

[11] 靳晓宁, 王磊, 孙长瑜. 组合阵栅瓣抑制方法研究[J]. 网络新媒体技术, 2011, 32(5): 19-26.

JI Xiaoning, WANG Lei, SUN Changyu. A grating lobe restrain method in large aperture compounding array[J]. Network New Media, 2011, 32(5): 19-26.

[12] Cotter S F, Rao B D, Engan K, et al. Sparse solutions to linear inverse problems with multiple measurement vectors[J]. IEEE Transactions on Signal Processing, 2005, 53(7): 2477-2488.

[13] 黄传禄, 晁坤, 毛云志. 基于压缩感知的空间谱估计[J]. 电波科学学报, 2014, 29(1): 150-157.

HUANG Chuanlu, CHAO Kun, MAO Yunzhi, The spatial spectrum estimation based on compressive sensing[J]. Chinese Journal of Radio Science, 2014, 29(1): 150-157.

MVDR based unambiguous direction finding method for non-uniform sparse array

LI Qian-ru, SONG Zhi-jie, WANG Liang,YANG Qing

(College of Information Science and Engineering, Ocean University of China, Qingdao 266100, Shandong, China)

Sparse array can get large aperture, but it will also lead to azimuth ambiguity if conventional beam-forming (CBF) is used for non-uniform sparse array. In order to solve this problem, the method called NUSA+MVDR is presented, in which minimal variance distortionless response (MVDR) is applied to non-uniform sparse array with local non-sparse element distribution(NUSA), and theoretical analysis indicates that false peaks could be suppressed by this method. For a typical NUSA(TNUSA), numerical simulations are carried out, and the results, which are in good agreement with theoretical analysis, show that: 1. MVDR has great detection performance, as the equivalent element spacing reaches to 50 times of the wavelength under the simulation condition given in this paper, TNUSA+MVDR can still suppress azimuth ambiguity perfectly; 2. Azimuth resolution of TNUSA+MVDR is higher than that of CBF and MVDR for a uniform non-sparse array with the same number of elements; 3. For the given number of array elements, the azimuth resolution of TNUSA+MVDR improves with the increase in equivalent element spacing, and the minimum resolvable angle is inversely proportional to the equivalent element spacing; 4.For the given equivalent element spacing, the azimuth resolution of TNUSA+MVDR improves with the increase in the number of array elements. The detection performance of NUSA+MVDR is verified partially by marine experiments under the condition where the equivalent array element spacing is 10 times of the wavelength.

non-uniform sparse array; Minimal Variance Distortionless Response (MVDR); passive direction finding

O427

A

1000-3630(2015)-05-0389-06

10.16300/j.cnki.1000-3630.2015.05.002

2015-04-21;

2015-07-17

声场声信息国家重点实验室基金(SKLA201406)

李倩茹(1990－), 女, 甘肃兰州人, 硕士研究生, 研究方向为水声信号处理。

李倩茹, E-mail: alice_lee_ouc@163.com