普通克里金法在海水温度剖面插值中的应用

杨雪峰，胡长青



普通克里金法在海水温度剖面插值中的应用

杨雪峰1,2，胡长青1

(1. 中国科学院声学研究所东海研究站，上海200032；2. 中国科学院大学，北京 100190)

海水温度剖面在水声学领域扮演着重要的角色，而目前大面积实时温度剖面测量能力尚存不足，因此对于海水温度剖面的网格插值研究就有一定的意义。基于普通克里金法对某海域获得的剖面样本进行插值，通过逐点逐面的拟合最终得到该海域三维温度场。通过拟合温度剖面和部分样本剖面的对比，证实普通克里金法对于海水温度剖面拟合具有很好的效果，具有应用的可行性。

海水温度剖面；普通克里金；空间插值

0 引言

声波在海水中的传播速度主要受温度、盐度、深度等因素的影响。其中温度的作用最大，因而温度剖面的测量是研究水声传播理论的必要工作。受技术条件的限制，现阶段国内还无法实现大面积实时海水温度剖面的测量，多数只能靠舰船走航获得测线上的离散剖面样本。利用样本数据空间插值得到三维温度场成为弥补技术条件受限的有效手段。刘强等[1-3]提出了一种适合空间数据插值的统计算法，在磁法数据格网化等领域内获得了良好的效果。本文基于普通克里金法[4]，探索其在海水三维温度场插值研究中的适用性。

1 基本理论

克里金方法是由法国地统计科学家Matheron提出，以纪念南非矿业工程师D. G. Krige在地矿评估领域的开创性工作[5]。它的基本原理就是利用半变异函数表示空间离散样本之间距离的变化来拟合经验半变异函数，通过无偏估计和最优估计变异函数计算各样本线性权重，最后用各样本及其权重表示未知点估计值。

在研究区域内，变量()在采样点x(=1,2,3,…,)处取值(x)。未知点变量由上述个已知变量值加权求和而得，如式(1)所示。

(2)

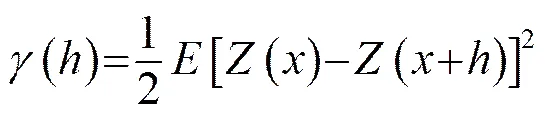
2 数据选择及适用性分析

本文采用南海某海域获得的85个有效温度剖面数据进行该海域的空间温度插值，采样点位置信息如图1所示，实际经纬度模糊处理。

克里金方法适用的一个先决条件是要分析的变量服从正态分布[5]。本文研究的温度剖面在每一层海水深度处都有离散值，为方便验证，取100、200、300和400 m四处样本值做QQ图。

结果如图2所示，各个水深处温度的分布与标准正态分位数成线性关系，表明运用克里金插值方法可以较好地实现海水空间温度插值[6]。

3 经验半变异函数拟合

3.1 最大分离距离和分组步长

要计算样本半变异函数云图，首先要确定最大分离距离和分组步长。以50 m处样本值为例，85个样本之间最大的距离间隔为118 km。那么按照步长选取原则，分组数与分组步长的乘积应该小于最大间隔距离的一半。通过反复试验，选取5 km为步长，将85个样本值分成11组。半变异函数散点如图3所示。

3.2 经验半变异函数模型

常用的模型函数有球面函数、指数函数、高斯函数和线性函数等，其表达式如下[7]：

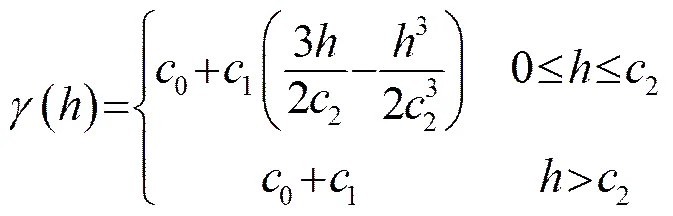
(5)

(6)

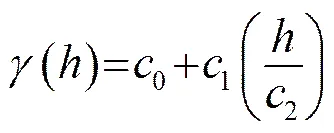
四个模型拟合数据的残差如表1所示。

通过对比以上拟合结果以及其他水深温度拟合结果，本文选择高斯模型用于海水温度空间差值。拟合得到的高斯函数表达式如下：

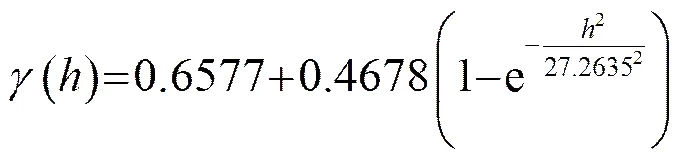
表1 不同模型拟合残差比较

4 空间温度插值

4.1 计算权重系数

在获得高斯函数模型的表达式之后，分别计算样本点之间的半变异函数值以及插值点与样本点之间的半变异函数值，将两者代入克里金方程组即式(2)便可求得权重系数以及拉格朗日系数。插值点的温度可以通过式(1)计算得到。

对50 m水深样本温度数据计算，首先将克里金方程组写成矩阵形式，表达式如式(9)所示。

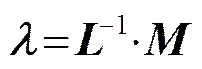
(10)

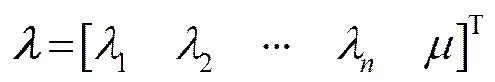
(12)

4.2 绘图

式(10)的矩阵中，个样本两两之间的半变异函数值组成半变异函数矩阵。改变矩阵的维数可以改变温度插值效果。图5所示的是3维半变异函数矩阵所求解出来的温度灰度图。当把维数改变为5维、7维时，获得的温度灰度图如图6、图7所示。

从图5~7可以看出，随着半变异矩阵维数的增加，插值点利用的样本数相应增多，带来的影响是插值拟合对比度的降低和平滑度的提高。式(13)给出了克里金估计方差的表达式，结果见表2。

表2 克里金估计方差

4.3 单点温度剖面拟合

将各深度温度拟合完成后，就得到了整个三维温度场的信息。对于拟合精度的计算，可以从样本空间中剔除单个样本，然后用其他样本点对其进行插值拟合。对比原数据与插值结果，如图8所示。

从剖面曲线可以看出，半变异矩阵维数对单点温度剖面拟合稍有影响。计算不同维数半变异矩阵对应剖面的平均绝对误差，如图9所示。从图9可以看出当维数为7时，平均绝对误差最小。随着维数的增多，计算单点温度值所需要的样本数也越来越多，但平均绝对误差趋于平稳。

5 结论

本文研究的海区内可以明显看出温度的空间分布特征，说明普通克里金法是海水温度空间插值一种有效的手段。插值效果依赖于海区样本密度、时效性和均匀度，密度越高，时效性越高以及分布越均匀，插值拟合效果也就越好。因此普通克里金法不仅对水平变化较缓的海区适用，当样本密度、时效性和均匀度理想的条件下，也适用于内波活动频繁或有孤子内波活动的海区。

[1] 刘强, 陶钧, 刘旭, 等. 基于克里金插值的磁法数据格网化研究[J]. 河南科学, 2013, 31(7): 1039-1044.

LIU Qiang, TAO Jun, LIU Xu, et al. Study on the gridding of magnetic method data based on interpolation principle of Kriging[J]. He’nan Science, 2013, 31(7): 1039-1044.

[2] 周艳霞, 笪良龙, 韩梅, 等. 基于ArcGIS的海水温度空间差值方法研究[J]. 声学技术, 2013, 32(5): 210-212.

ZHOU Yanxia, DA Lianglong, HAN Mei, et al. The research of the method of seawater temperature interpolation based on ArcGIS[J]. Technical Acoustics, 2013, 32(5): 210-212.

[3] 黄耀裔. 基于普通Kriging的地下水空间差值研究[J]. 廊坊师范学院学报: 自然科学版, 2013, 13(6): 12-17.

HUANG Yaoyi. Study on spatial interpolation of groundwater based on ordinary Kriging[J]. Journal of Langfang Teachers College: Natural Science Edition, 2013, 13(6): 12-17.

[4] 吴学文, 晏路明. 普通Kriging法的参数设置及变异函数模型选择方法——以福建省一月均温空间内插为例[J]. 地球信息科学, 2007, 9(3): 104-108.

WU Xuewen, YAN Luming. Setting parameters and choosing optimum semivariogram models of ordinary Kriging interpolation-A case study of spatial interpolation to January average temperature of Fujian province[J]. Geo-information Science, 2007, 9(3): 104-108.

[5] 王亭, 盛业华. 顾及各向异性的三维Kriging空间插值方法研究[D]. 南京: 南京师范大学: 1-65.

WANG Ting, SHENG Yehua. Research on 3D interpolation approaches based on Kriging with anisotropic spatial structures[D]. Nanjing: Nanjing Normal University: 1-65.

[6] 靳国栋, 刘衍聪, 牛文杰. 距离加权反比插值法和克里金插值法的比较[J]. 长春工业大学学报, 2003, 24(3): 53-57.

JIN Guodong, LIU Yancong, NIU Wenjie. Comparison between inverse distance weighting method and Kriging[J]. Journal of Changchun University of Technology, 2003, 24(3): 53-57.

[7] 胡庆芳, 胡艳, 杨大文, 等. 面向大范围降水空间插值的普通克里金模型开发与实例分析[J]. 应用基础与工程科学学报, 2014, 22(1): 106-116.

HU Qingfang, HU Yan, YANG Dawen, et al. A matlab based ordinary Kriging model developed for rainfall spatial interpolation over nacro regions and a case application[J]. Journal of Basic Science and Engineering, 2014, 22(1): 106-116.

Application of Ordinary Kriging method in the interpolation for seawater temperature profile

YANG Xue-feng1,2, HU Chang-qing1

(1. Shanghai Acoustic Laboratory, Institute of Acoustics, Chinese Academy of Sciences, Shanghai 200032, China;2.University of Chinese Academy of Sciences, Beijing 100190, China)

Seawater temperature profile plays an important role in underwater acoustics, while the ability of acquiring instant temperature profile in a large area is far from sufficient. Based on MATLAB, the Ordinary Kriging method is used to interpolate profiles acquired from a certain sea area point-to-point and surface-to-surface into a three-dimensional temperature field. Contrasting the interpolated profiles with the acquired ones, the OK method is tested to be effective for fitting the temperature profile with highly feasibility.

seawatertemperature profile; Ordinary Kriging; spacial interpolation

TB533

A

1000-3630(2015)-05-0385-04

10.16300/j.cnki.1000-3630.2015.05.001

2014-09-30;

2014-12-17

杨雪峰(1987－), 男, 山东烟台人, 硕士研究生, 研究方向为水声技术。

杨雪峰, E-mail: yangxuefeng12@mails.ucas.ac.cn